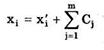Тех карта урока математики. 1. Понятие множества и элемента множества Множество

• Название: 1. Понятие множества и элемента множества Множество
• Анкор: Тех карта урока математики
• Дата: 04.05.2022
• Размер: 1.94 Mb.
• Имя файла: matematika_ekzamen.doc
• Тип: Документы; #511493
• страница: 6 из 6

А;   от   _Ндо   _В; Р,

где А – результат измерения в единицах измеряемой величины;

 ,   _Н,   _В – соответственно погрешность измерения с нижней и верхней ее границами в тех же единицах;

Р – установленная вероятность, с которой погрешность измерения находится в этих границах.

Пример: 121 м/с,  от – 1 до 2 м/с,

Р=0,99.

В общем случае  не равно  . Если границы погрешности симметричны, т.е.   , то результат измерения может быть записан так:

А   ; Р

Это одна из форм представления результата измерения. ГОСТ допускает и другие формы представления результата измерения, отличающиеся от приведенной формы тем, что в них указывают раздельно характеристики систематической и случайной составляющих погрешности измерения.

(1).2. Принципы оценивания погрешностей

Оценивание погрешностей производится с целью получения объ­ективных данных о точности результата измерения. Точность ре­зультата измерения характеризуется погрешностью. Погрешность измерения описывается определенной математической моделью, вы­бор которой обуславливается имеющимися априорными сведения­ми об источниках погрешности, а также данными, полученными в ходе измерений. С помощью выбранной модели определяются ха­рактеристики и параметры погрешности, используемые для количественного выражения тех или иных ее свойств.

Характеристики погрешности принято делить на точечные и интер­вальные. К точечным относятся СКО случайной погрешности я предел сверху для модуля систематической погрешности, к интервальным — границы неопределенности результата измерения. Если эти границы определяются как отвечающие некоторой доверительной вероятности, то они называются доверительными интервалами. Бели же минимально возможные в конкретном случае границы погрешности оценивают так, что погрешность, выходящую за них, встретить нельзя, то они называ­ются предельными (безусловными) интервалами.

В основу выбора оценок погрешностей положен ряд принципов. Во-первых, оцениваются отдельные характеристики и параметры вы­бранной модели погрешности. Это связано с тем, что модели погреш­ностей, как правило, сложны и описываются многими параметрами. Определение их всех весьма затруднительно, а иногда и невозмож­но. Кроме этого, в большинстве практических случаев полное описа­ние модели погрешности содержит избыточную информацию, в то время как знание отдельных ее характеристик вполне достаточно для достижения цели измерения. Во-вторых, оценки погрешности определяют приближенно, с точностью, согласованной с целью из­мерения. Это обусловлено тем, что погрешности определяют лишь зону неопределенности результата измерения и их не требуется знать очень точно. В-третьих, погрешности оцениваются сверху, поэтому погрешность лучше преувеличить, чем преуменьшить, так как в первом случае снижается качество измерений, а во втором — возможно полное обесценивание результатов всего измерения. В-четвертых, поскольку стремятся получить реалистические значения оценки погрешности результата измерения, т.е. не слишком завышенные и не слишком заниженные, точность измерений должна соответствовать рели измерения. Излишняя точность ведет к неоправданному расходу средств и времени. Недостаточная точность в зависимости от цели намерения может привести к признанию годным в действительности негодного изделия, к принятию ошибочного решения и т. п.

Оценивание погрешностей может проводится до (априорное) и после (апостериорное) измерения. Априорное оценивание — это проверка возможности обеспечить требуемую точность измерений, проводимых в заданных условиях выбранным методом с помощью кон­кретных СИ. Оно проводится в случаях:

• нормирования метрологических характеристик СИ;

• разработки методик выполнения измерений;

• выбора средств измерений для решения конкретной измери­тельной задачи;

• подготовки измерений, проводимых с помощью конкретного СИ.

Апостериорную оценку проводят в тех случаях, когда априор­ная оценка неудовлетворительна или получена на основе типовых метрологических характеристик, а требуется учесть индивидуаль­ные свойства используемого СИ. Такую оценку следует рассматри­вать как коррекцию априорных оценок.

(2).2. Способы обнаружения и устранения систематических погрешностей

Результаты наблюдений, полученные при наличии системати­ческой погрешности, называются неисправленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей. Это может быть дос­тигнуто следующими путями:

• устранением источников погрешностей до начала измерений.

В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключаю­щие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устра­нить систематические погрешности не путем обработки экспери­ментальных данных, а применением СИ, реализующих соответст­вующие методы измерений;

• определением поправок и внесением их в результат измерения;

• оценкой границ неисключенных систематических погрешностей.

Постоянная систематическая погрешность не может быть най­дена методами совместной обработки результатов измерений. Од­нако она не искажает ни показатели точности измерений, характе­ризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности. Дейст­вительно, результат одного измерения



где х_И — истинное значение измеряемой величины;   — i-я случай­ная погрешность;   — i-я систематическая погрешность. После ус­реднения результатов многократных измерений получаем среднее арифметическое значение измеряемой величины



Если систематическая погрешность постоянна во всех измере­ниях, т.е.   , то

Таким образом, постоянная систематическая погрешность не устраняется при многократных измерениях.

Постоянные систематические погрешности могут быть обнару­жены лишь путем сравнения результатов измерений с другими, по­лученными с помощью более высокоточных методов и средств. Ино­гда эти погрешности могут быть устранены специальными приемами проведения процесса измерений. Эти методы рассмотрены ниже.

Наличие существенной переменной систематической погрешно­сти искажает оценки характеристик случайной погрешности и ап­проксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений.

Исключение систематических погрешностей путем введения по­правок. В ряде случаев систематические погреш­ности могут быть вычис­лены и исключены из ре­зультата измерения. Для этого используются поправки. Поправка Cj – величина, одноименная измеряемой, которая вводится в результат измерения   с целью исключе­ния составляющих систематической погрешности   . При Cj = -   j-я составляющая систематической погрешности полностью уст­раняется из результата измерения. Поправки определяются экс­периментально или в результате специальных теоретических ис­следований. Они задаются в виде таблиц, графиков или формул.

Введением одной поправки устраняется влияние только одной составляющей систематической погрешности. Для устранения всех составляющих в результат измерения приходится вводить множе­ство поправок. При этом вследствие ограниченной точности опре­деления поправок случайные погрешности результата измерения накапливаются и его дисперсия увеличивается. Так как поправка известна с определенной точностью, то она характеризуется ста­тистически — средним значением поправки С и СКО S_c. При ис­правлении результата   путем введения поправок Cj, где j=l, 2,..., m, по формуле

дисперсия исправленного результата

где   — оценка дисперсии неисправленного результата;   — оценка дисперсии j-й поправки. Как видно, с одной стороны, уточ­няется результат измерения, а с другой — увеличивается разброс за счет роста дисперсии. Следовательно, необходимо найти опти­мум.

Пусть при измерении постоянной величины Q получено (рис. 5.1) значение   , где   — оценка среднего арифме­тического неисправленного результата измерений; t_p — коэффи­циент Стьюдента. 

После введения поправки С ± t_pS_c результат измерения



Рис. (2).1. Устранение систематической погрешности путем введения поправки

где

Максимальные доверительные значения погрешности результа­та измерения до и после введения поправки равны соответственно



Поправку имеет смысл вводить до тех пор, пока   . Отсюда следует, что



Если S_c/S « 1, то, раскладывая уравнение в степенной ряд, получим С > 0,5 Sc / S² . Из этого неравенства видно, что если оцен­ка среднего квадратического отклонения поправки   , то по­правку имеет смысл вводить всегда.

В практических расчетах погрешность результата обычно выра­жается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц младшего разряда, следующего за последним десятичным разрядом погрешности результата, все равно будет потеряна при округлении и вводить ее не имеет смыс­ла.