Тех карта урока математики. 1. Понятие множества и элемента множества Множество

• Название: 1. Понятие множества и элемента множества Множество
• Анкор: Тех карта урока математики
• Дата: 04.05.2022
• Размер: 1.94 Mb.
• Имя файла: matematika_ekzamen.doc
• Тип: Документы; #511493
• страница: 5 из 6

Б) Мы будем изучать простейшие выпуклые многогранники — призмы и пирамиды.

Призмой называется многогранник, две грани которого — равные  угольники, а остальные   граней — параллелограммы.

Равные грани-многоугольники призмы называют её основаниями, а остальные грани — боковыми гранями. Рёбра боковых граней, не принадлежащие основаниям, называются боковыми рёбрами (рис. 10).

В зависимости от количества сторон основания призмы отличают треугольную, четырёхугольную, пятиугольную и т. д. призмы. На рисунке 11 изображена шестиугольная призма.

Совокупность боковых граней призмы образуют боковую поверхность.

Площадь боковой поверхности призмы равна сумме площадей боковых граней.

Призмы разделяются на прямые и наклонные.

Прямая призма — призма, боковые грани которой являются прямоугольниками. Обычно, изображая прямую призму, её боковые рёбра проводят вертикально (рис. 12).

Призма прямая, если боковые рёбра перпендикулярны рёбрам основания призмы.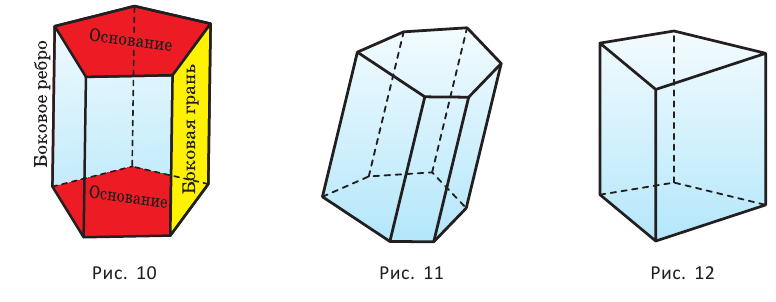



Призма наклонная, если боковые рёбра не перпендикулярны рёбрам основания призмы.

Прямая призма называется правильной, если её основания являются правильными многоугольниками.

Призма, основаниями которой являются параллелограммы, называется параллелепипедом.

Параллелепипед, как и призма, может быть и прямым (рис. 13), и наклонным (рис. 14).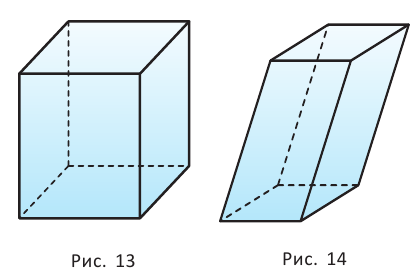



Прямой параллелепипед, основания которого являются прямоугольниками, называется прямоугольным параллелепипедом.

Все грани прямоугольного параллелепипеда являются прямоугольниками.

Три ребра прямоугольного параллелепипеда, сходящиеся в одной вершине, называются измерениями прямоугольного параллелепипеда.

Прямоугольный параллелепипед с равными измерениями называется кубом.

Все грани куба — равные друг другу квадраты.

В) Пирамидой называется многогранник, одна грань которого — многоугольник, а остальные являются треугольниками с общей вершиной.

На рисунке 15 изображена пирамида   Многоугольник   называют основанием пирамиды, треугольные грани   — боковыми гранями, а общую вершину   боковых граней — вершиной пирамиды. Обычно в записи обозначения пирамиды первая буква соответствует её вершине.

В зависимости от количества сторон основания пирамиды отличают треугольную, четырёхугольную, пятиугольную и т. д. пирамиды. Пирамида на рисунке 15 — пятиугольная, а на рисунке 16 — треугольная.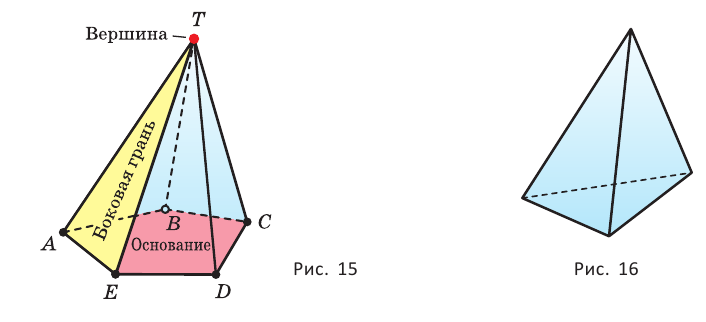



Пирамида, основание которой — правильный многоугольник, а отрезок, соединяющий её вершину с центром основания, перпендикулярен любой прямой, проведённой в плоскости основания через этот центр, называется правильной.

Высота боковой грани правильной пирамиды, опущенная из вершины пирамиды, называется апофемой пирамиды.

На рисунке 17 изображена правильная четырёхугольная пирамида 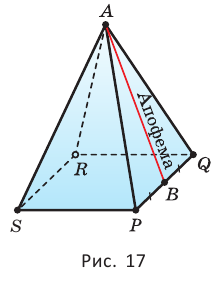  отрезок   — одна из её апофем.



Теорема 1. У правильной пирамиды равны её: а) боковые грани; б) апофемы.

Доказательство: Пусть   — правильная пирамида и точка   — центр её основания (рис. 18).

а) Поскольку треугольники   и   оба прямоугольные, имеют общий катет   и равные катеты   и   то они равны. Поэтому равны и их гипотенузы   и   Аналогично доказывается, что другие боковые рёбра также равны 

Боковые грани пирамиды — равнобедренные треугольники с равными боковыми сторонами. Основания этих треугольников также равны друг другу как стороны правильного многоугольника, который лежит в основании пирамиды. Поэтому боковые грани равны между собой по трём сторонам.

б) Поскольку боковые грани пирамиды 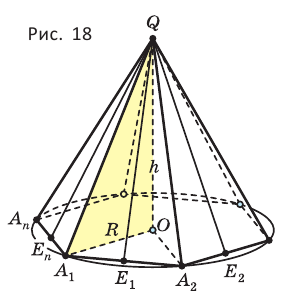  равны между собой, то равны и их высоты, проведённые из вершины   это значит, что все апофемы пирамиды   равны.



Теорема 2. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра её основания и апофемы.

Доказательство: Пусть 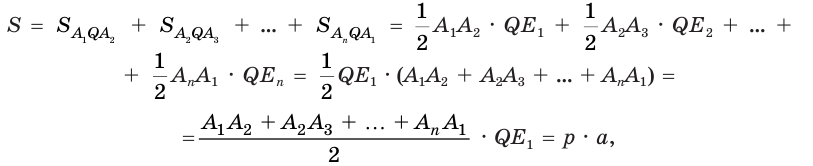  — правильная пирамида (см. рис. 18). Площадь   её боковой поверхности состоит из площадей боковых граней, которые являются равными друг другу равнобедренными треугольниками с равными апофемами   Поэтому



где  — полупериметр основания пирамиды,   — апофема пирамиды

Г) Ещё один класс пространственных фигур составляют тела вращения, к которым относятся цилиндр, конус, шар.

Цилиндром называется тело, полученное вращением прямоугольника вокруг одной из его сторон (рис. 19). При этом вращении одна сторона прямоугольника остаётся неподвижной, её называют осью цилиндра. Сторона, противолежащая оси, образует поверхность, которую называют боковой поверхностью цилиндра, а саму сторону — образующей цилиндра. Ещё две стороны прямоугольника при вращении образуют поверхности, которые являются равными кругами, эти круги называют основаниями цилиндра (рис. 20). На рисунке 21 дано изображение цилиндра.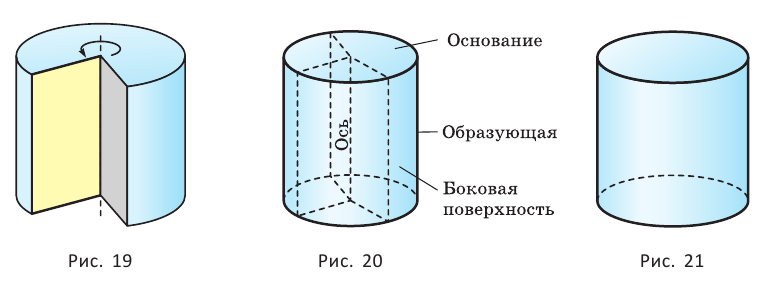



Конусом называется тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов (рис. 22), который называют осью конуса. Второй катет описывает круг, который называют основанием конуса; неподвижную вершину треугольника, которая не принадлежит основанию, называют вершиной конуса. Гипотенуза при вращении образует поверхность, которую называют боковой поверхностью конуса, саму гипотенузу называют образующей конуса (рис. 23). На рисунке 24 дано изображение конуса.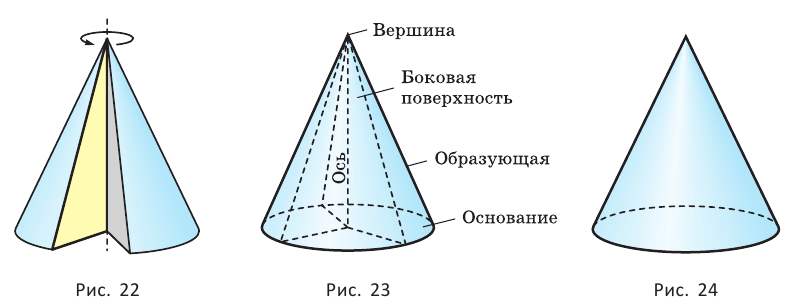



Шаром называется тело, полученное вращением круга вокруг своего диаметра (рис. 25). При этом вращении окружность описывает поверхность, которую называют сферой (рис. 26). На рисунке 27 дано изображение шара.

48.Изучение и построение геометрических фигур на плоскости.

Задачи на построение являются важным средством формирования у учащихся геометрических представлений в целом. В процессе геометрических построений учащиеся в практическом плане знакомятся со свойствами геометрических фигур и отношений, учатся пользоваться чертежными инструментами, приобретают графические навыки. В правильности многих математических утверждений в большинстве случаев школьники убеждаются также в процессе геометрических построений.

Рассмотрим решение задач на построение с помощью циркуля и линейки.

Основная цель – сформировать умение и развить навыки решения задач на построение с помощью циркуля и линейки.

Схема решения задачи на построении включает в себя следующие этапы: анализ, построение, доказательство, исследование.

Анализ: цель которого – составление плана решения, осуществляется по – разному при различных методах построения: иногда предполагают искомую фигуру построенной, иногда разбивают условие задачи на несколько частей и т.д.

Построение – осуществление плана решения задачи, составленного в результате анализа.

Доказательство – установление правильности решения, доказательство того, что полученное решение удовлетворяет условиям задачи.

Исследование – определение всевозможных случаев, допускаемых условиями задачи, и числа решений в каждом из этих случаев.

С точки зрения логики узловыми этапами решения задачи на построение являются два – анализ и доказательство. Рассмотрим эти этапы подробнее и установим тесную логическую взаимосвязь между ними. Анализ начинается с того, что требуемая фигура построена, т.е. выполнены все те свойства, которые сформулированы в условии задачи. В ходе анализа из этих свойств мы пытаемся извлекать какие-то выводы, и каждый такой вывод анализируем на то, можно ли от него вернуться к данному условию. Другими словами, мы ищем такие необходимые следствия данных условий задачи, которые, в свою очередь, для этих условий окажутся достаточными. Что же происходит при доказательстве? Выведенные в процессе анализа следствия становятся условиями. Из этих условий должны быть выведены те свойства, которые сформулированы в условии задачи. Таким образом, следствия анализа становятся условиями доказательства, а условия анализа – следствиями доказательства. Это означает, что в процессе анализа мы устанавливаем ряд прямых теорем, а в процессе доказательства используем обратные для них теоремы. Отсюда задача анализа выявить в его ходе такие теоремы, обратные утверждения для которых сами будут справедливы, т.е. сами будут теоремами.

Из этой логики вытекает методика обучения решению задач на построение. Указать учащимся на эту логическую связь анализа и доказательства и предложить им каждый раз обнаруживать и четко формулировать прямые теоремы в ходе анализа и обратные для них теоремы в ходе доказательства. Если навык такого подхода будет выработан, то учащиеся будут отчетливо представлять логику решения задач на построение и свою задачу на каждом этапе решения.

Предположим, что в качестве средств построения выбраны циркуль и линейка. Сначала выбираются первичные неопределяемые понятия. Такими являются понятия построенных основных фигур, т.е. каждая из фигур, участвующих в условии задачи, считается изначально построенной. Далее формулируются правила, по которым к имеющимся фигурам с использованием циркуля и линейки можно строить новые фигуры. Вот эти правила (постулаты).

(П1). Если есть две различные точки А и В, то можно построить отрезок АВ, прямую АВ и четыре луча.

(П2). Если есть три точки А, В, С (В не равно С), то можно построить окружность с центром в точке А с радиусом, равным отрезку ВС.

(П3). Если построены две непараллельные прямые, то можно найти точку их пересечения.

(П4). Если построены пересекающиеся прямая и окружность, то можно найти точки их пересечения (в частности, на данной прямой отложить отрезок, равный данному отрезку).

(П5). Если построены две пересекающиеся окружности, то имеем точки их пересечения.

Методы решения задач на построение.

Метод геометрических мест– состоит в том, что задача сводится к отысканию некоторой точки, характеризуемой условием.

Метод применения движения (параллельный перенос, поворот, осевая симметрия) – состоит в том, что предполагая искомую фигуру построенной, подбирают такое движение, в результате которого образуется некоторая вспомогательная фигура, удовлетворяющая двум условиям:

а) она может быть построена по данным задачи;

б) она связана с искомой фигурой. Таким образом, что, будучи сама построенной, позволяет построить и искомую фигуру.

Метод подобия – состоит в том, что условие задачи разбивают на две части, одна из которых определяет «форму» искомой фигуры, а другая – ее размеры. По первой части условия строят фигуру, подобную искомой, затем преобразовывают ее в искомую с учетом второй части условия.

Метод алгебраический – этот метод заключается в том, что в искомой геометрической фигуре выделяется отрезок, угол или отношение отрезков при этом длина этого отрезка выражается через длины данных отрезков по некоторой формуле. Для того, чтобы построить выделенный отрезок в искомой геометрической фигуре нужно провести построение отрезка, длины которых задаются формулами.

Основные задачи на построение, решение которых даются в школьном курсе математики.

• 
  Отложить отрезок вдоль данного отрезка АВ равный данному СД.
  
• 
  Построить сумму и разности данных отрезков.
  
• 
  Отложить от данного отрезка угол равный данному.
  
• 
  Построить сумму и разность двух углов.
  
• 
  Найти середину отрезка.
  
• 
  Построить биссектрису угла.
  
• 
  Восстановить перпендикуляр к прямой к данной ей точке.
  
• 
  Опустите перпендикуляр из данной точки на данную прямую.
  
• 
  Провести из данной точки параллельной данной.
  
• 
  Разделите данный отрезок в данном отношении в заданном как отношение данного отрезка а:в или как отношение целых чисел m:n.
  

49.Определение линий регрессии методом наименьших квадратов для двумерных выборок

Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное.  Уравнение линейной регрессии имеет вид

y=ax+b

a, b – коэффициенты линейного уравнения регрессии;

x – независимая переменная;

y – зависимая переменная.

Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов: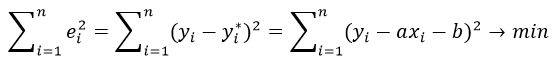



частные производные функции приравниваем к нулю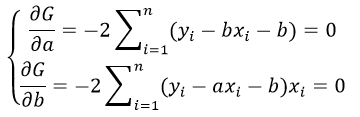



отсюда получаем систему линейных уравнений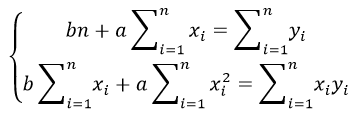



Формулы определения коэффициентов уравнения линейной регрессии: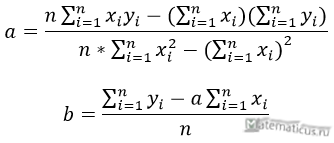



Также запишем уравнение регрессии для квадратной нелинейной функции: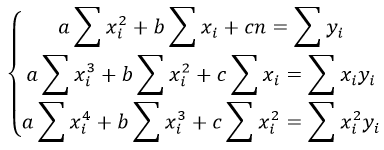



Система линейных уравнений регрессии полинома n-ого порядка: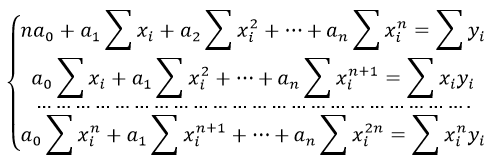



Формула коэффициента детерминации R²: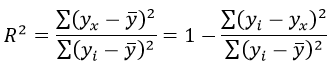



Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):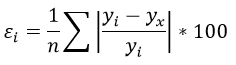



Чем меньше ε, тем лучше. Рекомендованный показатель ε<10%
Формула среднеквадратической погрешности: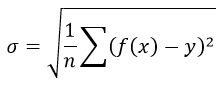


50. Методы оценки погрешности.

ГОСТ 8.011 – 84 устанавливает следующие показатели точности измерений.

интервал, в котором погрешность измерения находится с заданной вероятностью;

интервал, в котором систематическая составляющая погрешности измерения находится с заданной вероятностью;

числовые характеристики систематической составляющей погрешности измерения;

числовые характеристики случайной составляющей погрешности измерения;

Функция распределения (плотность вероятности) систематической составляющей погрешности измерения;

Функция распределения (плотность вероятности) случайной составляющей погрешности измерения.

При выражении точности измерений интервалом, в котором с установленной вероятностью находится суммарная погрешность измерения, устанавливается следующая форма представления результатов измерения: