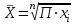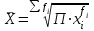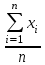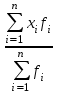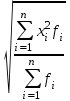менеджмент. 1 Предмет и задачи статистики
 Скачать 407.71 Kb. Скачать 407.71 Kb.
|
|
Тема 3 Статистическая сводка и группировка Цель: изучить методы сводки и группировки данных статистических наблюдений, рассмотреть основные виды статистических рядов распределения и статистических таблиц, правила построения таблиц. План: 1. Понятие сводки, виды сводки 2. Понятие, значение и задачи метода группировок 3. Виды группировок 4. Статистические ряды распределения 5. Статистические таблицы. Правила оставления статистических таблиц 1. Понятие сводки, виды сводки Статистическая сводка – это научно-организованная обработка материалов наблюдения, включающая в себя систематизацию, группировку данных, составление таблиц, подсчет групповых и общих итогов, расчет производных показателей (средних, относительных величин). Она позволяет перейти к обобщающим показателям совокупности в целом и отдельных её частей, осуществлять анализ и прогнозирование изучаемых процессов. Различают следующие виды сводки: по сложности построения (или по глубине обработки материала): простая и вспомогательная; по технике (способу) выполнения: ручная и механизированная (с помощью ПК); по форме обработки материалов: централизованная и децентрализованная. Статистическая сводка проводится по определенной программе и плану. Программа статистической сводки устанавливает следующие этапы: 1) выбор группировочных признаков; 2) определение порядка формирования группы; 3) разработка системы статистических показателей для характеристики групп и объекта в целом; 4) разработка макетов статистических таблиц для представления результатов сводки. План статистической содержит указания о последовательности и сроках выполнения отдельных частей сводки, ее исполнителях и о порядке изложения и представления результатов. 2. Понятие, значение и задачи метода группировок Статистическая группировка - расчленение единиц изучаемой совокупности на однородные группы по определенным существенным для них признакам. Значение метода группировок состоит в том, что данный метод обеспечивает обобщение данных, представляет их в компактном, обозримом виде. Кроме того, группировка создает основу для последующей сводки и анализа данных. Этим и определяется роль группировок как научной основы сводки. С помощью метода группировок решаются следующие основные задачи: выделение социально-экономических типов явлений; изучение структуры явления и структурных сдвигов, происходящих в нем; изучение связей и зависимостей между отдельными признаками явления. 3. Виды группировок Различают три вида группировок: типологические, структурные, аналитические. Типологическая группировка решает задачу выявления и характеристики социально-экономических типов путем разделения качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки. Признаки, по которым производится распределение единиц изучаемой совокупности на группы, называются группировочными признаками или основанием группировки. Структурнойназывается группировка, характеризующая состав однородной совокупности по какому-либо варьирующему признаку. Она позволяет изучать: интенсивность вариации группировочного признака и динамику структуры совокупности. Аналитические (факторные) группировкиизучают взаимосвязи между явлениями и их признаками. В основе аналитической группировки лежит факторный признак и каждая выделенная группа характеризуется средними значениями результативного признака. Принципы построения статистических группировок. I этап. Построение группировки начинается с определения состава группировочных признаков. II этап. Определение количества групп, на которые надо разбить исследуемую совокупность. III этап. Определение интервалов группировки. Интервал – значение варьирующего признака, лежащего в определенных границах. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей– наибольшее значение признака в интервале. Величина интервала – разность между верхней и нижней границами интервала. Интервалы группировки в зависимости от их величины могут быть равные и неравные. Если вариация признака проявляется в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами. Если размах вариации признака велик и значения признака варьируются неравномерно, то строят группировку с неравными интервалами. Интервалы могут быть закрытыми, когда указаны нижние и верхние границы, и открытыми, когда указана одна из границ (первый или последний интервал). 4. Статистические ряды распределения Статистический ряд распределения – упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Различают: атрибутивные и вариационные ряды распределения. Атрибутивные ряды распределения- ряды распределения, построенные по качественным признакам (в порядке возрастания или убывания). Вариационныминазывают ряды распределения, построенные по количественному признаку. Вариационные ряды распределения состоят из двух элементов: вариантов (числовые значения количественного признака, принимающего в ряду распределения) и частот (численности отдельных вариантов). Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности. Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные. Дискретные вариационные рядыоснованы на дискретных (прерывных) признаках, имеющих в большинстве случаях целые значения, на дискретных признаках, представленных в виде интервалов. Интервальные вариационные ряды– основаны на непрерывных признаках, имеющих множество значений, в т.ч. и дробные. 5. Статистические таблицы. Правила составления статистических таблиц Результаты статистической сводки и группировки материалов излагаются в виде таблиц, которые являются наиболее рациональной формой изложения. В них наглядно проявляется связь между признаками изучаемого явления. Статистическая таблица – форма рационального и наглядного изложения цифровых характеристик исследуемых явлений и его составных частей. Значение таблиц определяется тем, что они позволяют рассматривать совместно изолированные статистические данные, достаточно полно и точно охватывая сложную природу явлений. Основная особенность табличного изложения состоит в том, что характеризуемые в таблице показатели можно объединить под одним общим заголовком. Внешне таблицы представляют собой пересечение граф и строк. Записав заголовки граф и строк, получают макет таблицы. Составление макетов статистических таблиц – важнейшее условие планирования разработки статистических материалов. Далее макет заполняется соответствующими данными статистической сводки. Статистическая таблица имеет подлежащее и сказуемое. Подлежащее таблицы – это перечень единиц совокупности или группы, т.е. объект изучения. Сказуемым таблицы являются числовые значения, характеризующие подлежащее. Обычно подлежащее располагается слева в виде названий строк, сказуемое – сверху в виде названий граф. Однако, при большом перечне элементов подлежащего и небольшом сказуемом для характеристики групп на одной странице – их меняют местами. Обязательной составной частью таблицы является общий заголовок, который кратко характеризует содержание таблицы. Различают заголовок всей таблицы, заголовки подлежащего – боковые и заголовки сказуемого – верхние. В зависимости от разработки статистического подлежащего или от группировки единиц в подлежащем различают три вида таблиц: 1) простые (перечневые, территориальные, хронологические; 2) групповые; 3) комбинационные. По разработке сказуемого, которая может простой и сложной. Различают следующие требования (правила) к составлению и оформлению таблиц: 1) Таблица по возможности должна быть краткой. Не рекомендуется загромождать ее излишними подробностями, затрудняющими анализ исследуемых явлений; 2) Каждая таблица должна иметь подробное название, из которого определяется: а) круг вопросов, излагаемый и иллюстрируемый таблицей; б) географические границы статистической совокупности, представленные таблицей; в) период времени, за который приведены данные или момент времени, к которому они относятся; г) единицы измерения, если они одинаковы для всех табличных клеток (если единицы измерения неодинаковы, то в верхних или боковых заголовках обязательно указывается, в каких единицах приводятся статистические данные – тоннах, штуках, тенге и пр.); 3) В таблице рекомендуется давать нумерацию граф, что облегчает пользование таблицей, дает возможность лучшего восприятия, демонстрирует способ расчета чисел в графах. Первые графы, содержащие подлежащее, обозначаются заглавными буквами алфавита; графы, содержащие сказуемое, нумеруются арабскими цифрами. Заглавия строк подлежащего и граф сказуемого должны быть сформулированы кратко, точно и ясно. Все слова в заголовках подлежащего и сказуемого таблицы записываются по возможности полностью; 4) Приводимые в подлежащем и сказуемом признаки должны быть расположены в логическом порядке с учетом необходимости рассматривать их совместно. Обычный принцип размещения – сначала показывают слагаемые, а в конце подводят итоги (если это необходимо). Когда приводятся не все слагаемые, а лишь наиболее важные из них, применяется противоположный принцип: сначала показывают общие итоги, а затем выделяют наиболее важные части («В том числе», «Из них»). Следует различать «Итого» и «Всего». «Итого» является итогом для определенной части совокупности, «Всего» - итог для совокупности в целом; 5) Таблица может сопровождаться примечаниями. Если данные заимствованы, то под таблицей указывается источник. Может быть примечание к таблице, в котором раскрывается методика расчета показателей, а также даются подтверждающие пояснения по тем показателям, которые могут вызвать вопросы; 6) При оформлении таблиц обычно применяются следующие условные обозначения: а) знак тире (-) – когда явление отсутствует; б) х – если явление не имеет осмысленного содержания; в) многоточие (…) – когда отсутствуют сведения о его размере (или делается запись «Нет сведений»). Если сведения имеются, но числовое значение меньше принятой в таблице точности, оно выражается дробным числом (0,0). Округленные числа приводятся в таблице с одинаковой степенью точности (до 0,1, до 0,01 и т.п.). Литература: 2, с. 35-36; 5, с. 76-114; 18, с. 18-60 Контрольные вопросы: В чем суть и каково значение сводки? Какие существуют виды группировки? Что такое вторичная группировка? Что представляют собой статистические ряды распределения, и по каким признакам они могут быть образованы? Что представляют собой статистические таблицы, и каковы ее составные элементы? Какие различают виды статистических таблиц, их применение в анализе и обобщении данных. Что называют макетом таблицы. Какие требования предъявляют к оформлению статистических таблиц? Тема 4 Абсолютные и относительные величины Цель: рассмотреть основные виды абсолютных и относительных величин, их использование в статистических исследованиях, представление показателей в виде различных графиков. План: 1. Сущность и значение абсолютных величин, их виды и единицы измерения 2. Сущность и значение относительных величин. Формы выражения и виды относительных величин. 3. Графическое изображение абсолютных и относительных величин 1. Сущность и значение абсолютных величин, их виды и единицы измерения Абсолютный размер явления – это отдельно взятая его величина, не зависящая от размеров других явлений. Относительный размер– это соотношение величины данного явления с величиной какого-нибудь другого явления или с величиной самого же явления, но взятой за другое время или по другой местности. Статистические величины, выражающие размеры явлений в единицах меры (веса, объема, протяженности, площади, стоимости и т.п.) называются абсолютными статистическими величинами. Различают три вида абсолютных величин: индивидуальные, групповые и общие. Групповые и общие иногда называют итоговыми или суммарными. Индивидуальными называют абсолютные величины, которые выражают размеры количественных признаков у отдельных единиц изучаемой совокупности. Групповые и общие абсолютные величины выражают величину того или иного признака у всех вместе взятых единиц данной совокупности или у отдельных их групп либо численность единиц всей совокупности или отдельных ее частей (групп). Существует разграничение моментных и интервальных абсолютных величин. Моментные показывают фактическое наличие или уровень явления на определенный момент, дату. Интервальные – итоговый накопленный результат за период в целом. В отличие от моментных, интервальные абсолютные величины допускают их последующее суммирование (если речь идет об одном и том же показателе). Выделяют три типа единиц измерения: натуральные, денежные (стоимостные) и трудовые. Натуральными называют единицы измерения, которые выражают величину предметов, вещей и т.п. в физических мерах, т.е. мерах веса, объема, длины, площади и т.д. в соответствии с их физическими свойствами. В ряде случаев применяются условные натуральные единицы измерения, которые применяются для сведения нескольких разновидностей одной и той же потребительской стоимости в одну. Ее принимают за эталон, а другие пересчитываются с помощью специальных коэффициентов в единицы меры этого эталона. Денежные единицы измерения используются для характеристики в стоимостном (денежном) выражении многих статистических показателей. При использовании стоимостных измерителей учитывается изменение цен с течением времени посредством «неизменных» или «сопоставимых» цен. Трудовые единицы измерения – человеко-час, человеко-день, человеко-год и т.п. используются для измерения затрат труда на производство продукции, на выполнение какой-либо работы, для определения уровня производительности труда; величины трудовых ресурсов, рациональности их использования и др. 2. Сущность и значение относительных величин. Формы выражения и виды относительных величин. Относительными статистическим величинами называют величины, выражающие количественные соотношения между социально-экономическими явлениями, их признаками. Они получаются в результате деления одной величины на другую, чаще всего – отношения двух абсолютных величин. Величина, с которой производится сравнение (знаменатель дроби) называется основанием относительной величины, базой сравнения или базисной величиной, та которая сравнивается – текущей, сравниваемой или отчетной величиной. Относительная величина показывает, во сколько раз сравниваемая величина больше базисной или какую долю, первая составляет от второй, в некоторых случаях – сколько единиц одной величины приходится на 100, на 1000 и т.д. единиц другой, базисной величины. Относительные величины получаются в результате сопоставления одноименных и разноименных величин. При одноименных – получаются величины, не имеющие размерности; выражаются в виде кратного отношения, показывающего, во сколько раз одна величина больше или меньше другой (с которой она сравнивается). Широко распространенной формой выражения относительных величин являются процентные отношения, при которых базисная величина принимается за 100. Часто относительные величины выражаются в форме промилле - основание принимается за 1000 и обозначается знаком 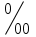 . .В результате сопоставления некоторых разноименных величин получаются именованные относительные величины. В зависимости от содержания (т.е. какие соотношения выражают относительные величины) выделяют основные их виды: относительные величины динамики; относительные величины планового задания; относительные величины выполнения плана; относительные величины структуры; относительные величины интенсивности; относительные величины уровня экономического развития; относительные величины сравнения; относительные величины координации. Относительной величиной динамики называют отношение уровня (значения) показателя за данное время (год, квартал, месяц и т.п.) к его уровню за предыдущее время. Она характеризует направление изменения явлений во времени, скорость этого изменения, т.е. – темп развития. В зависимости от характера базы сравнения, различают два вида относительных величин: относительные величины динамики с переменной базой сравнения – цепные; относительные величины динамики с постоянной базой сравнения – базисные. Относительная величина планового задания представляет собой отношение величины показателя, устанавливаемого на планируемый период, к его величине, достигнутой в планируемом периоде, или какой-либо другой, принятой за базу сравнения. Относительной величиной выполнения плана называется величина, выражающая соотношение между фактическим и плановым уровнями показателя. Эти величины, обычно, выражаются в процентах. Относительные величины динамики, планового задания и выполнения плана связаны соотношением: 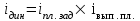 Относительные величины структуры представляют собой соотношение размеров частей и целого. При их вычислении в качестве базы сравнения берется величина целого, общий итог по какому-либо показателю, а сравниваемыми являются значения показателей отдельных частей этого целого. Иначе относительная величина структуры называется долей или удельным весом. Относительные величины интенсивности или степени, характеризуют степень распространения, развития какого-либо явления в определенной среде. Данные величины представляют собой соотношение разноименных величин. В числителе берется величина явления (показателя), степень распространения которого изучается, а в знаменателе – объем той среды, в которой происходит развитие (распространение) этого явления. Относительными величинами уровня экономического развития называют показатели, характеризующие размеры производства различных видов продукции на душу населения. Относительные величины сравнения представляет собой отношение одноименных величин, характеризующих разные объекты. Относительные величины координации называют соотношение частей целого между собой. Одну из составных частей целого принимают за базу сравнения и находят отношение к ней всех других частей. 3. Графическое изображение абсолютных и относительных величин Графиками в статистике называются условные изображения числовых величин и их соотношений в виде различных геометрических образов – точек, линий, плоских фигур и т.п. Статистический график включает заголовок, в котором указывается, что представлено на графике, к какой территории и к какому времени относятся данные. Каждый график состоит из графического образа и вспомогательных элементов. Графический образ – это совокупность точек, линий и фигур, с помощью которых изображаются статистические данные. Вспомогательными элементами графика являются: 1) поле графика; 2) пространственные ориентиры; 3) масштабные ориентиры; 4) экспликация графика состоит из объяснения: а) предмета, изображаемого графиком (его названия); б) смыслового значения каждого знака, применяемого на данном графике. Статистические графики классифицируются:1) по назначению или содержанию: а) графики сравнения в пространстве; б) графики различных относительных величин (структуры, динамики и т.п.); в) графики вариационных рядов; г) графики размещения по территории; д) графики взаимосвязанных показателей. 2) по способу построения: а) диаграммы; б) картодиаграммы. 3) по характеру графического образа: а) точечные; б) линейные; в) плоскостные (столбиковые, квадратные, круговые, секторные, фигурные); г) объемные. Литература: 2, с. 45-47; 5, с. 159-165; 18, с. 75-79. Контрольные вопросы: 1. Абсолютные величины, их значение в статистических исследованиях. 2. Какие виды абсолютных величин Вы знаете?. 3. Виды относительных величин, способы их расчета и формы выражения. 4. Проблема сопоставимости относительных величин и выбор базы сравнения. 5. Область применения относительных величин 6. Основные виды графиков. 7. Какова роль графиков в обобщении и анализе данных?. Элементы графика. Тема 5 Средние величины и показатели вариации Цель: Рассмотреть основные виды индексов и показателей вариации, их применение и использование в статистике. План: 1. Средние величины: сущность, значение, виды 2. Показатели вариации, сущность, значение, виды.Законы вариации 3. Моменты. Ассиметрия и эксцесс 4. Законы распределения 1. Средние величины: сущность, значение, виды Важный вклад в обоснование и развитие теории средних величин внес крупный ученый XIX века Адольф Кетле (1796-1874), член Бельгийской академии наук, член-корреспондент Петербургской академии наук. Средняя величина - обобщающая характеристика изучаемого признака в исследуемой совокупности. Она определяет его типичный уровень в расчёте на единицу совокупности в конкретных условиях места и времени. Средняя величина всегда именованная, имеет ту же размерность (единицу измерения), что и признак у отдельных единиц совокупности. Основным условием научного использования средней величины является качественная однородность совокупности, по которой исчислена средняя. Существуют две категории средних величин: степенные (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя кубическая); структурные (мода, медиана). Степенная средняя – корень степени k из средней всех вариантов, взятых в k–й степени, имеет следующий вид: 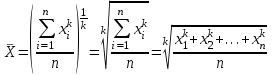 . .где 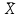 – признак, по которому находится средняя, называется осредняемым признаком, – признак, по которому находится средняя, называется осредняемым признаком,хiили (х1,х2…хn) – величина осредняемого признака у каждой единицы совокупности, fi – повторяемость индивидуального значения признака. В зависимости от степени k получаются различные виды степенных средних, формулы расчета которых показаны ниже в таблице 1. Таблица 1 – Виды степенных средних
fi – частота повторения индивидуального значения признака (его вес) Весом может быть и частотость, т.е. отношение частоты повторения индивидуального значения признака к сумме частот: 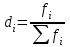 Выбор вида средней величины: Средняя арифметическая простая применяется в случае, если индивидуальное значение признака у единиц совокупности на повторяется или встречается одни раз или одинаковое число раз, т.е. когда средняя рассчитывается по несгруппированным данным. Когда отдельное значение изучаемого признака встречается несколько раз у единиц изучаемой совокупности, тогда частота повторения индивидуальных значений признака (вес) присутствует в расчетных формулах степенных средних. В этом случае они называются формулами взвешенных средних. Если по условию задачи необходимо, чтобы неизменной оставалась при осреднении суммы величин, обратных, индивидуальным значениям признака, то средняя величина является гармонической средней. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить среднюю геометрическую. Средняя геометрическая используется для расчета средних темпов роста в анализе рядов динамики. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной. Средняя квадратическая используется для расчета среднего квадратического отклонения при анализе вариации признака в рядах распределения. Степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные и чем больше показатель степени k, тем больше и величина соответствующей средней, если все исходные значения признака равны, то и все средние равны этой постоянной: 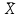 гарм. ≤ гарм. ≤ 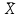 геом. ≤ геом. ≤ 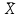 арифм. ≤ арифм. ≤ 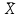 кв. ≤ кв. ≤ 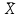 куб. куб.Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется мажорантностью средних. Структурные средние применяют в том случае, когда расчет степенных средних невозможен или нецелесообразен. К структурным средним относят: моду и медиану. Мода – это наиболее часто встречающееся значение признака у единиц данной совокупности. При наличии вариантов и частот в ряду распределения величина моды соответствует значению признака у наибольшего числа единиц (наибольшей частоте), т.е. для дискретного вариационного ряда мода находится по определению. Медиана – значение признака у единицы совокупности в середине ранжированного ряда распределения, когда все индивидуальные значения признака изучаемых единиц расположены в порядке их возрастания или убывания. В случае нечетного числа наблюдений медиана находится по определению, т.е. вариант 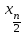 (где n – число наблюдений). При четном числе наблюдений медиана определяется по формуле: (где n – число наблюдений). При четном числе наблюдений медиана определяется по формуле: 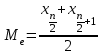 Для интервального ряда распределения величина моды и медианы рассчитываются по следующим формулам: 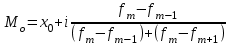 ; ; 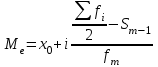 , , где: 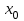 - нижняя граница модального или медианного интервала; - нижняя граница модального или медианного интервала;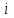 - величина интервала; - величина интервала;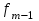 и и 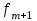 - частоты, предшествующие и следующие за модальным интервалом; - частоты, предшествующие и следующие за модальным интервалом;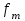 - частота модального или медианного интервала; - частота модального или медианного интервала;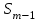 - сумма накопленных частот в интервалах, предшествующих медианному. - сумма накопленных частот в интервалах, предшествующих медианному.Расчет медианы по несгруппированным данным производится следующим образом: 1. Индивидуальные значения признака располагаются в возрастающем порядке. 2. Определяется порядковый номер медианы № Ме = (n+1) / 2 Показатели вариации, сущность, значение, виды.Законы вариации Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям (мера) вариации относятся: размах колебаний, среднее абсолютное отклонение, дисперсия, среднее квадратическое отклонение. Размах вариации – это разность между максимальным и минимальным значениями признака: 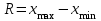 . .Размах вариации показывает, в каких пределах колеблется размер признака, образующего ряд распределения Среднее абсолютное отклонение (САО) - средняя из абсолютных значений отклонений отдельных вариант от средней. 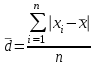 (простая), (простая), 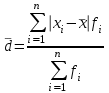 (взвешенная) (взвешенная)Дисперсия- средняя из квадратов отклонений вариантов значений признака от их средней величины: 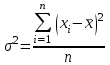 (простая), (простая), 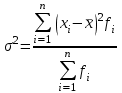 (взвешенная) (взвешенная)Дисперсия может быть разложена на составные элементы, позволяющих оценить влияние различных факторов, обуславливающих вариацию признака 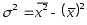 т.е. дисперсия равна разности между средним квадратом значений признака и квадратом средней. Свойства дисперсии, позволяющие упростить способ ее вычисления: Дисперсия постоянной величины равна 0. Если все варианты значений признака уменьшить на одно и то же число раз, то дисперсия не уменьшится. Если все варианты значений признака уменьшить в одно и то же число раз (k раз), то дисперсия уменьшится в k2 раз. Среднее квадратическое отклонение (СКО) представляет собой корень квадратный из дисперсии, показывает насколько в среднем колеблется величина признака у единиц изучаемой совокупности: = 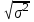 СКО является мерилом надежности. Чем меньше СКО, тем лучше средняя арифметическая отражает собой всю представляемую совокупность. 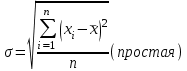 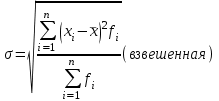 Размах вариации, САО, СКО являются величинами именованными, т.е. имеют те же единицы измерения, что и индивидуальные значения признака. Существуют 4 вида дисперсии: общая, межгрупповая, внутригрупповая, групповая. Дисперсию, вычисляемую для всей совокупности в целом называют общей дисперсией. Она измеряет колеблемость зависимого признака (результатного), вызванную действием на него всех без исключения факторов. О 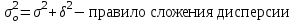 бщая дисперсия равна сумме средней из внутригрупповой и межгрупповой дисперсии: бщая дисперсия равна сумме средней из внутригрупповой и межгрупповой дисперсии:Если совокупность разбита на группы, то для каждой группы может быть определена своя дисперсия, характеризующая вариацию внутри группы. Групповая дисперсия – средние квадратические отклонения от групповой средней, т.е. от средней величины признака в данной группе. 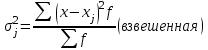 где j – порядковый номер x и fв пределах группы. Групповая дисперсия характеризует вариацию признака в пределах группы за счет всех прочих факторов, кроме положенного в основании группировки. 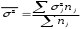 Измерение вариации по совокупности в целом, исчисляем как среднюю из внутригрупповых дисперсии: Измерение вариации по совокупности в целом, исчисляем как среднюю из внутригрупповых дисперсии:где 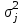 – групповые дисперсии, – групповые дисперсии,nj – число единиц в группах. Групповые средние отличаются одна от другой и от общей средней, т.е. варьируют. Их вариацию называют межгрупповой вариацией. Для ее характеристики исчисляют средний квадрат отклонений групповых средних от общей средней: 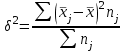 где 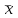 j – групповые средние, j – групповые средние, 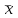 – общая средняя,nj – число единиц в группе. – общая средняя,nj – число единиц в группе.Межгрупповая дисперсия (дисперсия групповых средних) измеряет вариацию результатного признака за счет факторного признака, положенного в основании группировки. При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации. Эти показатели вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) Коэффициент вариации 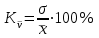 Относительное линейное отклонение 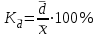 Коэффициент осцилляции 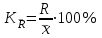 Наиболее часто применяемый показатель относительной колеблемости – коэффициент вариации, который показывает среднее отклонение от среднего значения признака в процентах. Его используют для: сравнительной оценки вариации; характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%, т.е. меньше 33%. 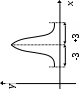 Законы вариации. Законы вариации.Закон вариации индивидуальных значений признака или «правило трех сигм». Бельгийский статистик А.Кетле обнаружил, что вариации некоторых массовых явлений подчиняются закону распределения ошибок, открытому К.Гауссом и П. Лапласом почти одновременно. Кривая, отображающая это распределение, имеет вид колокола (рис.2). По нормальному закону (термин предложен английским статистиком К.Пирсоном) распределения колеблемость индивидуальных значений признака находится в пределах 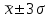 (правило трех сигм). (правило трех сигм).Нормальному закону распределения подчиняются естественные свойства человека (рост, вес, физическая сила), характеристики промышленных изделий (размер, вес, электрическое сопротивление, упругость и т.п.). В сфере быстроизменяющихся общественных явлений действие этого закона проявляется сравнительно редко. Однако, в ряде случаев, использование правила трех сигм практически возможно. | ||||||||||||||||||||||

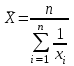
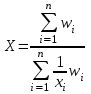 , wi = xi · fi
, wi = xi · fi