менеджмент. 1 Предмет и задачи статистики

• Название: 1 Предмет и задачи статистики
• Анкор: менеджмент
• Дата: 20.09.2022
• Размер: 407.71 Kb.
• Имя файла: 03 Ð_екÑ_ионнÑ_й комплекÑ_ (1).doc
• Тип: Тезисы; #687816
• страница: 5 из 5

Связи между явлениями, их признаками подразделяют по степени тесноты связей, направлению, аналитическому выражению

По степени тесноты связи выделяют функциональную и корреляционную связи.

Функциональными называют такие связи, в которых определенному значению факторного признака соответствуют вполне определенные значения результативного признака. Функциональная связь является строгой, полной, точной зависимостью.

Характерной особенностью функциональных связей является то, что известен полный перечень факторов, определяющих величину результативного признака, а также механизм этого влияния, выраженный определенным уравнением.

Для социально-экономических явлений характерно то, что наряду с существенными факторами, определяющими, в основном, величину результативного признака, на него оказывают воздействие многие другие, в том числе и случайные, факторы. Поэтому существующая зависимость не проявляется в каждом отдельном случае, а лишь, в общем, и среднем при большом числе наблюдений. В таких случаях связи называются стохастическими (вероятностными), при которых с изменением факторного признака меняется распределение единиц совокупности по результативному признаку. Частным случаем стохастической связи является корреляционная (статистическая связь), при которой каждому значению факторного признака могут соответствовать несколько значений результативного признака. При этом изменение независимой величины влечет за собой изменение среднего значения зависимого показателя. Следовательно, корреляционная связь является «неполной» зависимостью, которая проявляется в средних величинах при достаточно большом числе случаев.

По направлению выделяют связь прямую и обратную. Прямой называют такую связь, при которой оба вида признаков (факторный и результативный) изменяются в одном и том же направлении – по мере увеличения или уменьшения значения факторного признака значения результативного, соответственно, увеличиваются или уменьшаются.

В случае же обратной связи значения результативного показателя изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака.

По аналитическому выражению связи бывают прямолинейные (линейные) и нелинейные. При линейной связи зависимость между факторным и результативным признакам и может быть выражена в виде уравнения прямой, а при криволинейной – в виде уравнения кривой (гиперболы, параболы и т.п.).
2. Методы выявления связи между признаками

Для изучения стохастических связей используется метод параллельных рядов, метод аналитических группировок, графический, построение корреляционных таблиц.

Метод сравнения параллельных рядов. Сущность данного метода заключается в том, что сначала показатели, характеризующие факторный признак, располагаются в порядке возрастания или убывания (ранжируются), затем параллельно им располагаются соответствующие значения результативного показателя. Сравнение построенных таким образом рядов дает возможность не только подтвердить само наличие связи, но и выявить ее направление.

Метод аналитических группировок. Производится группировка единиц совокупности по признаку-фактору и для каждой группы вычисляется средняя или относительная величина результативного показателя. Сопоставляя затем изменение результативного признака по мере изменения признака-фактора, можно выявить направление и характер связи между ними.

Корреляционная таблица. Факторный признак (х) располагают в строках, а результативный признак (у) – в столбцах (графах) таблицы. Числа, расположенные на пересечении строк и столбцов таблицы, означают частоту повторения данного сочетания х и у. Если частоты в таблице расположены на диагонали из левого верхнего угла в правый нижний угол (т.е. большим значениям фактора соответствуют большие значения функции), то можно предположить о наличии прямой корреляционной зависимости между признаками. Если же частоты расположены по диагонали справа налево, то предполагают наличие обратной связи между признаками.

Для предварительного выявления наличия связи применяют графический метод. Используя данные об индивидуальных значениях признака-фактора и соответствующих ему значениях результативного признака, можно построить в прямоугольных координатах точечный график, который называют «полем корреляции». Соединяя последовательно отрезками прямых соответствующие точки, получаем эмпирическую линию связи.
3. Корреляционно-регрессионный анализ связи между признаками: сущность, значение, этапы

Метод анализа корреляций и регрессий – корреляционно-регрессионный анализ (КРА) заключается в построении и анализе экономико-математической модели в виде уравнения регрессии (корреляционной связи), выражающего зависимость явления от определяющих его факторов: у_х = f(x₁, x₂…..x_n)

КРА состоит их следующих этапов:

1. 
   предварительный анализ свойств моделируемой совокупности единиц
   
2. 
   установление факта наличия связи, определение ее направления и формы
   
3. 
   определение параметра уравнения связи с помощью решения системы нормальных уравнений
   
4. 
   измерение степени тесноты связи между признаками
   
5. 
   построение регрессионной модели
   
6. 
   оценка и анализ модели
   

Рассмотрим данные этапы.

1. 
   Исследуется рассматриваемое явление до сбора исходной информации, т.е.: формируется задача исследования, например, изучение влияния различных факторов на уровень производительности труда; определяется методика измерения результативного показателя.
   
2. 
   у_х = ах + ab  n линейная
   

у_х = ax² bx + c параболическая и т.д., т.е. решается вопрос о выборе (установлении) формы связи.

3) Для нахождения параметров уравнения регрессии используется метод наименьших квадратов, который предполагает решение системы нормальных уравнений. Для прямой нормальные уравнения МНК имеют вид: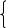

na + bx_i = y_i

ax_i + bx_i² = x_iy_i

Линейные связи являются основными. Но встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой и т.д.

4) Степень тесноты связи измеряется с помощью линейного коэффициента корреляции, например, в случае наличия линейной зависимости между признаками, определяется по формуле: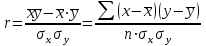

, где: n- число наблюдений.

Для практических вычислений при малом числе наблюдений, 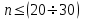, линейный коэффициент корреляции удобнее вычислять по формуле: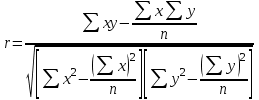



Линейный коэффициент принимает любые значения от 1 до 1. Чем ближе к 1, тем теснее связь между признаками.

Если коэффициент  (0;0,4, (0;0,4, связь слабая.

Если коэффициент  (0,4;0,7), (0,4;0,7), связь средняя.

Если коэффициент  0,7;1), 0,7;1), связь сильная, тесная.
Литература: 2, с. 311-317; 5, с. 217-243; 18, с. 237-273.

Контрольные вопросы:

1. Назовите задачи статистики по изучению взаимосвязей.

2. Какие виды связи вы можете перечислить?

3. Что такое множественная регрессия, анализ ее коэффициентов.

4. Назовите разницу между линейной и функциональной связью.