Закон вариации средних величин. Вариация средних величин меньше вариации индивидуальных значений признака. Средние значения признака изменяются в пределах: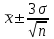 , где n – число единиц. , где n – число единиц.
3. Моменты. Ассиметрия и эксцесс
Моменты – обобщающие характеристики, определяющие характер распределения.
 Различают начальные, начальные относительно Различают начальные, начальные относительно 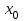 (условные), и центральные моменты. Начальные моменты (условные), и центральные моменты. Начальные моменты 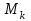 : : 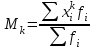 . Центральные моменты ( . Центральные моменты (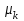 ): ): 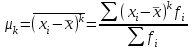 . Центральный момент . Центральный момент 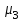 используется для числового измерения ассиметрии используется для числового измерения ассиметрии 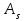 , которая определяется как отношение: , которая определяется как отношение: 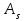 = =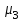 . Ассиметрия характеризует «скошенность» распределения. Величина показателя . Ассиметрия характеризует «скошенность» распределения. Величина показателя 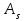 может быть положительной (рис.3 б) и отрицательной (рис.3 а). может быть положительной (рис.3 б) и отрицательной (рис.3 а).
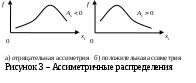
(островершинности).
Для симметричных распределений рассчитывается показатель эксцесса Эксцессом называется величина: 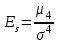 -3, которая характеризует островершинность или плосковершинность распределения, так называемую «крутость». -3, которая характеризует островершинность или плосковершинность распределения, так называемую «крутость».
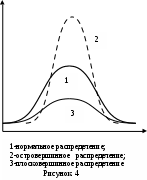
Для нормального закона 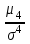 =3, таким образом =3, таким образом 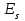 =0. Распределения более островершинные, чем нормальное, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом. На рис. 4 представлены островершинное (величина эксцесса положительная) и плосковершинное (величина эксцесса отрицательная) распределения. =0. Распределения более островершинные, чем нормальное, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом. На рис. 4 представлены островершинное (величина эксцесса положительная) и плосковершинное (величина эксцесса отрицательная) распределения.
4. Законы распределения
Законы распределения являются обобщающей характеристикой вариации в однородной совокупности.
Нормальное распределение. Распределение признака в совокупности называется нормальным, если этот признак представляет собой результат воздействия многочисленных и многообразных факторов, которые мало связаны друг с другом и влияние каждого из них незначительно по сравнению с общим влиянием всех факторов. Аналитически нормальное распределение описывается следующим образом: 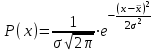 . .
Литература: 2, с. 60-62; 5, с. 178-196, 201-214;18, с.85-119;
Контрольные вопросы:
1. Значение средних величин в статистических исследованиях. Виды средних.
2. Средняя арифметическая, ее виды и основные свойства.
3. Средняя гармоническая, область ее применения.
4.Структурные средние, их значение и использование в анализе статистических показателей.
5. Назовите показатели степени колеблемости значений признака.
7. Относительные показатели вариации, их значение и условия применения.
8. Дайте определение дисперсии и назовите ее основные свойства.
9. Сформулируйте правило сложения дисперсий и условия его практического использования.
10. Что такое дисперсия альтернативного признака?
Тема 6 Выборочное наблюдение
Цель: Изучить основные виды, способы проведения выборочного наблюдения, методы отбора единиц в выборочную совокупность.
План:
Понятие выборочного наблюдения, его задачи.
2. Методы и способы отбора.
3. Определение ошибок выборочного наблюдения при различных видах выборки
4. Определение необходимой численности выборки
Понятие выборочного наблюдения, его задачи
Выборочное наблюдение - такое несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются не все единицы изучаемой совокупности, а лишь часть, отобранная в определенном порядке. Наблюдение организовано таким образом, что эта часть отобранных единиц в уменьшаемом масштабе репрезентирует (представляет) всю совокупность.
Преимущества выборочного наблюдения: экономия времени и средств в результате сокращения объема работы; сведение к минимуму порчи или уничтожения исследуемых объектов (определение прочности пряжи при разрыве, испытание электрических лампочек на продолжительность горения и т.п.); достижение большей точности результатов обследования благодаря сокращению ошибок, происходящих при регистрации.
Выборочное наблюдение следует проводить в строгом соответствии с научными принципами теории выборочного метода. Такими принципами являются: обеспечение случайности (равной возможности попадания в выборку) отбора единиц и достаточного их числа. Соблюдение этих принципов позволит получить достаточную гарантию репрезентативности полученной выборочной совокупности. Понятие репрезентативности отобранной совокупности означает: ее представительство в отношении тех признаков, которые изучаются или оказывают существенное влияние на формирование сводных обобщающих характеристик.
Основная задача выборочного наблюдения состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности.
Однако, при любых статистических исследованиях (сплошных и выборочных) возникают ошибки двух видов: регистрации и репрезентативности.
Ошибки регистрации могут иметь случайный (непреднамеренный) и систематический (тенденциозный) характер. Случайные ошибки обычно уравновешивают друг друга, т.к. не имеют преимущественного направления в сторону преувеличения или снижения значения изучаемого показателя. Систематические ошибки направлены в одну сторону, вследствие преднамеренного нарушения правил отбора (предвзятые цели). Их избегают при правильной организации и проведении наблюдения.
Ошибки репрезентативности присущи только выборочному наблюдению и возникают вследствие того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между величинами выборочных и соответствующих генеральных показателей.
Характеристики генеральной и выборочной совокупностей. Совокупность отобранных единиц называют выборочной совокупностью, а совокупность единиц, из которых производится отбор, - генеральной совокупностью.
Генеральная и выборочная совокупности характеризуются своими показателями: долей, средним размером признака, дисперсией и др. Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается p. Выборочная доля обозначается через w. Выборочная доля называется также частостью.
Средний размер в генеральной совокупности называют генеральной средней и обозначают 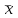 , средний размер в выборочной совокупности – выборочной средней, обозначаемой , средний размер в выборочной совокупности – выборочной средней, обозначаемой 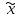 . .
С определенной вероятностью можно судить о величине разности между генеральными и выборочными характеристиками на основе предельных теорем. Предельные теоремы исходят из нормального распределения величин. Нормальное распределение показывает, что большая часть величин сосредотачивается около генеральной средней. Около 68,3% численности выборочных средних не будет выходить за пределы 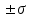 генеральной средней; 95,4% этой численности будет заключено в пределах генеральной средней; 95,4% этой численности будет заключено в пределах 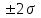 и 99,7% их не выйдет за пределы и 99,7% их не выйдет за пределы 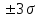 . Нормальное распределение имеет довольно общий характер и показывает частоту появления ошибок данного размера средней. . Нормальное распределение имеет довольно общий характер и показывает частоту появления ошибок данного размера средней.
Определение ошибок выборочного наблюдения при различных видах выборки
Расхождение между выборочной средней и генеральной средней. Теорема Чебышева-Ляпунова. Расхождения между выборочными и генеральными характеристиками называют ошибками.
Теорема Чебышева применительно к выборочному наблюдению утверждает, что ошибка репрезентативности – разность между выборочной средней и генеральной средней – при достаточно большом числе наблюдений будет сколь угодно малой, т.е. 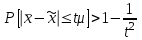 , ,
где 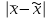 - абсолютная величина расхождения между генеральной средней и выборочной средней, составляющая ошибку репрезентативности; - абсолютная величина расхождения между генеральной средней и выборочной средней, составляющая ошибку репрезентативности;
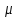 - среднее квадратическое отклонение вариантов выборочной средней от генеральной средней (средняя ошибка выборки). Оно зависит от колеблемости признака в генеральной совокупности - среднее квадратическое отклонение вариантов выборочной средней от генеральной средней (средняя ошибка выборки). Оно зависит от колеблемости признака в генеральной совокупности 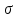 и числа отобранных единиц n: и числа отобранных единиц n: 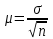 . Эта запись показывает, что о величине расхождения можно судить лишь с определенной вероятностью, которая зависит от коэффициента доверия t. Если выбратьt=2, то вероятность того, что это расхождение не превысит . Эта запись показывает, что о величине расхождения можно судить лишь с определенной вероятностью, которая зависит от коэффициента доверия t. Если выбратьt=2, то вероятность того, что это расхождение не превысит 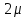 , будет не меньше чем 0,75, если t=3, то вероятность превысит 0,89 и т.д. , будет не меньше чем 0,75, если t=3, то вероятность превысит 0,89 и т.д.
Теорема была доказана П.Л. Чебышевым только для независимых событий, т.е. производстве повторной выборки. Позднее академиком А.А. Марковым было доказано сохранение этого условия для зависимых событий (бесповторной выборки).
Академик А.М. Ляпунов доказал, что вероятность отклонений выборочной средней от генеральной средней при достаточно большом числе отобранных единиц подчиняется закону нормального распределения. Из теоремы Ляпунова следует, что вероятность этих отклонений при разных значениях t может определяться по формуле: 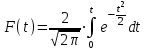
Значения этого интеграла при разных значениях t табулированы и даются в специальных таблицах. Вероятность для некоторых t (из таблицы):
при t=1 F(t)=0,683, при t=1,5 F(t)=0,866,
при t=2 F(t)=0,954, при t=2,5 F(t)=0,988,
при t=3 F(t)=0,997, при t=3,5 F(t)=0,999.
Доверительное число t указывает, что расхождение не превысит кратную ему среднюю ошибку выборки 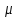 . Если t=1, то расхождение между выборочной средней и генеральной средней не превысит . Если t=1, то расхождение между выборочной средней и генеральной средней не превысит 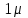 . Это может быть прочитано и так: с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превысит одной величины средней ошибки выборки. Другими словами, в 683 случаях из 1000 ошибка репрезентативности не выйдет за пределы . Это может быть прочитано и так: с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превысит одной величины средней ошибки выборки. Другими словами, в 683 случаях из 1000 ошибка репрезентативности не выйдет за пределы 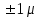 . С вероятностью 0,997 (довольно близкой к единице) можно ожидать, что разность между выборочной и генеральной средними не превзойдет трехкратной средней ошибки выборки. . С вероятностью 0,997 (довольно близкой к единице) можно ожидать, что разность между выборочной и генеральной средними не превзойдет трехкратной средней ошибки выборки.
Средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Величина 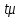 , обозначаемая , обозначаемая 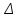 , называется предельной ошибкой выборки, которая определяется формулой , называется предельной ошибкой выборки, которая определяется формулой 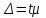 . С увеличением t увеличивается вероятность и величина ошибки. . С увеличением t увеличивается вероятность и величина ошибки.
Предельная ошибка выборки позволяет определять предельные значения характеристик генеральной совокупности при заданной вероятности и их доверительные интервалы: 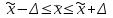
Генеральная средняя (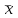 ) отличается от выборочной средней ( ) отличается от выборочной средней (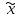 ) на величину предельной ошибки выборки: ) на величину предельной ошибки выборки: 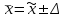
Это означает: с заданной вероятностью можно утверждать, что значение генеральной средней можно ожидать в пределаx от 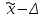 до до 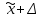 , то есть что доверительные интервал ( , то есть что доверительные интервал (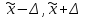 ) с заданной вероятностью заключает в себе генеральную среднюю. ) с заданной вероятностью заключает в себе генеральную среднюю.
Расхождение между частостью и долей. Теорема Бернулли рассматривает ошибку выборки для альтернативного признака, т.е. признака, у которого возможны только два исхода: наличие признака (1) и его отсутствие (0). Т.е. при достаточно большом объеме выборки по мере его увеличения вероятность расхождения между долей признака в выборочной совокупности w и долей признака в генеральной совокупности p будет стремиться к единице. Математически теорема Бернулли выглядит следующим образом: 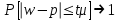
Иными словами: с вероятностью, сколько угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки частость признака (выборочная доля) сколько угодно мало отличается от его вероятности (доли в генеральной совокупности).
Поскольку 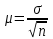 , а среднее квадратическое отклонение в генеральной совокупности для альтернативного признака равно , а среднее квадратическое отклонение в генеральной совокупности для альтернативного признака равно 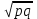 , где q=1–p, то средняя ошибка выборки для альтернативного признака выражается следующей формулой: , где q=1–p, то средняя ошибка выборки для альтернативного признака выражается следующей формулой: 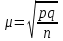
Поскольку дисперсия доли признака генеральной совокупности (pq) неизвестна, то дисперсию альтернативного признака принимают за w(1–w), тогда формула средней ошибки выборки: 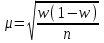
Предельная величина разности между частостью и долей называется предельной ошибкой выборочной доли. О ее величине можно судить, некоторой вероятностью, определив ее по формуле: 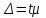 . .
Зная выборочную долю признака (w) и предельную ошибку выборки (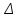 ), можно определить границы, в которых заключена генеральная доля p: ), можно определить границы, в которых заключена генеральная доля p:
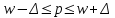 . .
Средняя ошибка случайной выборки: а) повторный отбор 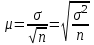
б) бесповторный отбор 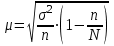
где N – число единиц в генеральной совокупности
n –число единиц в выборочной совокупности
При механическом отборе ошибка выборки рассматривается по формуле собственно-случайной бесповторного отбора.
Средняя ошибка пропорциональной типической выборки определяется по формулам:
а) повторный отбор: 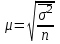 ; б) бесповторный отбор: ; б) бесповторный отбор: 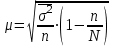 , ,
где 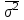 - средняя из внутригрупповых дисперсий в выборочной совокупности. - средняя из внутригрупповых дисперсий в выборочной совокупности.
Средняя ошибка серийной выборки :
а) повторный отбор: 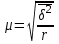 ; б) бесповторный отбор: ; б) бесповторный отбор: 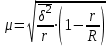 , ,
гдеR –общее число серий в генеральной совокупности
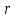 - число отобранных серий; - число отобранных серий;
Межсерийная дисперсия вычисляется по формуле: 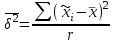
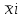 - групповые дисперсии, - групповые дисперсии, 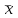 - общая средняя - общая средняя
3. Методы и способы отбора
Систему организации отбора единиц из генеральной совокупности называют способом отбора.
Различают методы отбора: повторный и бесповторный.
Повторным называется такой метод отбора, при котором отобранная однажды единица возвращается обратно в генеральную совокупность и снова участвует в выборке. При повторном отборе сохраняется постоянной вероятность попасть в выборку для всех единиц отбора.
Бесповторным называется такой метод отбора, при котором отобранная однажды единица в совокупность, из которых производится отбор, обратно не возвращается. При отборе каждой новой единицы вероятность попасть в выборку изменяется (увеличивается).
По виду отбора различают: 1) индивидуальный – отбор единиц совокупности; 2) групповой – отбор групп единиц; 3) комбинированный – комбинация первого и второго видов.
Различные виды отбора могут осуществляться разными способами проведения выборки. По способу отбора различают следующие виды выборочного наблюдения: случайная выборка, механическая выборка, типическая выборка, серийная выборка, комбинированная выборка.
При собственно-случайной выборке генеральную совокупность строго подразделяют на единицы отбора, а затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц (случайный порядок – порядок равносильный жеребьевке).
Механическая выборка заключается в отборе единиц из генеральной совокупности, производимом в каком-либо механическом порядке, например в отборе каждой пятой, десятой, пятнадцатой и т.д. единицы, при определенном расположении единиц в генеральной совокупности.
Под типической выборкой понимается такая выборка, когда перед ее проведением генеральная совокупность делится на группы по какому-либо типическому признаку (на типические группы), а затем внутри каждой группы производится случайная выборка. Из всех типических групп можно отбирать число единиц, пропорциональное их численностям и непропорциональное. В зависимости от этого различают пропорциональный и непропорциональный типический отбор. Типическая выборка может быть также повторной и бесповторной.
Сущность серийной выборки заключается в том, что вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение.
Серийная выборка может проводиться в порядке повторного и бесповторного отбора. Серии могут быть равновеликими и неравновеликими.
Комбинированная выборка. Комбинированная выборка предполагает использование нескольких способов выборки. Можно комбинировать, например, серийную (групповую) выборку и случайную (с индивидуальным отбором единиц совокупности). В этом случае, разбив генеральную совокупность на серии (группы) и отобрав нужное число серий, производят случайную выборку единиц в сериях. Такая комбинированная выборка может быть повторной (для групп единиц) и бесповторной.
Определение необходимой численности выборки.
Средняя квадратическая (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности. Уменьшение стандартной ошибки выборки, а следовательно и увеличение точности оценки, всегда связано с увеличением объёма выборки. В этой связи уже на стадии организации выборочного наблюдения решается вопрос о том, каков должен быть объём выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений.
Необходимая численность повторной случайной выборки: 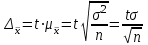 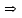 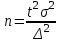
Эта формула показывает, что с увеличением допустимой ошибки выборки значительно уменьшается необходимый объем выборки. Так, увеличение ошибки выборки в 3 раза уменьшает необходимый объем выборки в 9 раз.
При случайном, механическом бесповторном отборе численность выборки 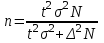 . .
Численность типической выборки при случайном бесповторном или механическом отборе внутри типов определяется: 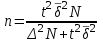 , ,
где: 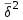 - средняя из внутригрупповых дисперсий, - средняя из внутригрупповых дисперсий, 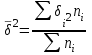 , ,
где: ni - число единиц в группах; 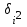 -групповые дисперсии -групповые дисперсии
Объем выборки из типических групп при отборе,, пропорциональном численности единиц типических групп: 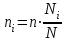 ; ;
где: ni-объём выборки из типической группы; n- общий объем выборки
Ni- объем типической группы; N- объём генеральной совокупности
Численность серийной выборки: а) повторный отбор 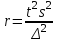
б) бесповторный отбор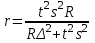 , где , где 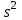 - межсерийная дисперсия Литература: 2; 5, с. 222-242; 18 - межсерийная дисперсия Литература: 2; 5, с. 222-242; 18
Контрольные вопросы:
1. Назовите теоретические основы проведения выборочного наблюдения
2. Сформулируйте основную идею выборочного наблюдения, его преимущества и недостатки.
3. Классифицируйте типы и виды выборочного наблюдения.
4.Назовите принципы отбора единиц выборки.
5. Дайте понятие ошибок выборочного наблюдения, методы их определения доверительный интервал
Модуль 2 - Статистические методы взаимосвязи социально-экономических явлений
Тема 7 Ряды динамики
Цель: Рассмотреть основные виды рядов динамики, методы их выравнивания, способы расчета показателей динамики.
План:
1. Понятие о рядах динамики, их виды и построение
2. Показатели рядов динамики и методы их выравнивания
3. Методы анализа основной тенденции развития
1. Понятие о рядах динамики, их виды и построение
Ряд динамики – ряд расположенных в хронологической последовательности значений статистических показателей.
Ряд динамики состоит из двух элементов:
1) моментов времени (обычно дат)или периодов времени (годы, кварталы, месяцы), к которым относятся статистические данные;
2) статистические показатели, характеризующие изучаемое общественное явление на тот момент или за тот период. Они называются уровнями ряда. Статистические показатели, приводимые в динамическом ряду, могут быть абсолютными, средними или относительными величинами.
Оба элемента – время и уровень – называются членами ряда динамики.
По времени, отражаемому в динамических рядах они подразделяются на моментные и интервальные.
В моментных рядах динамики уровни ряда выражают величину явления на определенную дату. В них время обозначает момент, к которому относится каждый уровень ряда.
В интервальных рядах уровни ряда выражают размеры явления за определенный промежуток времени.
По полноте времени, отражаемого в рядах динамики их делят на ряды полные и неполные. В полных рядах даты или периоды следуют друг за другом с равным интервалом. В неполных рядах в последовательность времени равный интервал не соблюдается;
По способу выражения уровней рядов динамики различают ряды абсолютных, средних и относительных величин.
При формировании динамических рядов надо соблюдать правила их построения. Одним из главных требований является сопоставимость уровней динамического ряда между собой. Для несопоставимых уровней нельзя вести расчеты показателей динамики.
К числу основных задач, возникающих при изучении динамических рядов, относятся следующие: 1) характеристика интенсивности отдельных изменений в уровнях ряда от перехода к периоду или от даты к дате; 2) определение средних показателей временного ряда; 3) выявление закономерностей динамики ряда в целом; 4) интерполяция (определение некоторых неизвестных уровней внутри данного динамического ряда) и экстраполяция (прогноз на будущее исходя из тенденции развития в прошлом); 5) выявление факторов, обусловливающих изменение изучаемого явления во времени.
2. Показатели анализа рядов динамики
В результате сравнения уровней получается система абсолютных и относительных показателей динамики.
К числу абсолютных и относительных показателей динамики относятся абсолютный прирост, коэффициент роста, темп прироста, абсолютное значение одного процента прироста, рассчитываемые базисным и цепным способами.
Таблица 4 - Абсолютные и относительные показатели динамики
Наименование показателя, его обозначение
|
Комментарий к расчету показателя
|
Формула расчета и его характеристика
|
Базисный способ
|
Цепной способ
|
Абсолютный прирост, 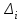 (или скорость роста) (или скорость роста)
|
Определяется как разность между двумя уровнями динамического ряда
|
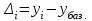
|
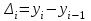
|
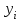 - уровень сравниваемого периода; - уровень сравниваемого периода;
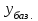 - уровень базисного периода; - уровень базисного периода;
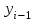 - уровень непосредственно предшествующего периода. - уровень непосредственно предшествующего периода.
Показывает, насколько данный уровень ряда превышает уровень, взятый за базу сравнения/предшествующий уровень
|
Коэффициент роста, 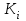
|
Определяется как отношение двух сравниваемых уровней
|
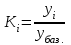
|
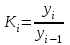
|
Показывает, во сколько раз данный уровень превышает уровень базисного периода/предшествующего периода
|
Темп роста, 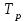
|
тот же, что и к коэффициенту роста, но выраженный в процентах
|
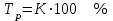
та же, что и коэффициента роста, но выраженная в процентах
|
Темп прироста,
|
а) отношение абсолютного прироста к базисному или предшествующему уровню
б) разность между темпом роста в процентах и 100%
|
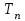 = =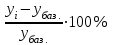
|
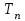 = =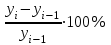
|
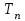 = =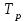 -100% -100%
Показывает, на сколько процентов уровень данного периода больше (или меньше) базисного уровня/предшествующего уровня
|
Абсолютное значение 1% прироста, 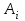
|
Рассчитывают как отношение абсолютного прироста к темпу прироста (в %) за тот же период времени
|
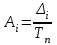 или или 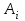 = =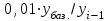
Оценивает значение полученного темпа прироста в сопоставлении с показателем абсолютного прироста
|
Для обобщающей характеристики динамики исследуемого явления определяют средние показатели, среди которых выделяют две категории:
- средние уровни ряда; - средние показатели изменения уровней ряда.
Средние уровни ряда.
а) Для интервального ряда абсолютных показателей средний уровень за период определяется по формуле простой средней арифметической: 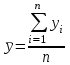
где n – число уровней ряда.
б) Средний уровень моментного полного динамического ряда определяется по формуле средней хронологической:
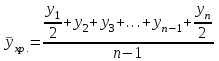 , ,
где n – число дат; 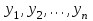 - уровни ряда в последовательные моменты времени. - уровни ряда в последовательные моменты времени.
в) Средний уровень моментного ряда с неравными промежутками между временными датами (неполный динамический ряд) вычисляется по средней арифметической взвешенной. В качестве весов берется число периодов времени между моментами, в которые происходят изменения в уровнях динамического ряда: 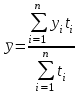 где где 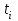 - количество дней (месяцев) между смежными датами. - количество дней (месяцев) между смежными датами.
Средние показатели изменения уровней ряда.
а) Средний абсолютный прирост (или средняя скорость темпа) рассчитывается как средняя арифметическая из показателей скорости роста за отдельные промежутки времени: 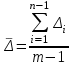 где n – число уровней ряда; где n – число уровней ряда;
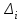 - абсолютные приросты по сравнению с предшествующим уровнем. - абсолютные приросты по сравнению с предшествующим уровнем.
Поскольку 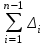 = =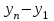 , тогда приведенную выше формулу можно преобразовать в следующий вид: , тогда приведенную выше формулу можно преобразовать в следующий вид: 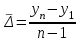
где 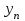 и и 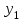 - соответственно конечный и начальный уровни динамического ряда. - соответственно конечный и начальный уровни динамического ряда.
б) Средний коэффициент роста вычисляется по формуле средней геометрической из показателей коэффициентов роста за отдельные периоды:
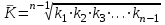 , ,
где 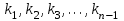 - коэффициенты роста по сравнению с уровнем предшествующего периода; - коэффициенты роста по сравнению с уровнем предшествующего периода;
n – число уровней ряда
в) Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах: 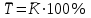
где 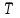 - средний годовой темп роста. - средний годовой темп роста.
г) Средний годовой тем прироста определяют на основании данных о среднегодовых темпах роста. Он показывает, на сколько процентов в среднем изменялся уровень ряда: 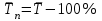
3. Методы анализа основной тенденции развития
Различают следующие методы выявления основной тенденции развития: укрупнение интервалов, скользящая средняя, аналитическое выравнивание, выравнивание по среднегодовому абсолютному приросту.
Метод укрупнения интервалов. При укрупнении интервалов времени вместо годовых данных берут сведения, например, за пятилетия, - и получают новый ряд динамики за пятилетие данных, показывающий последовательное их изменение. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.
Метод скользящей средней. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3,5,7 и т.д.), первых по счёту уровней ряда, затем- из такого же числа уровней, но начиная со второго по счёту, далее – начиная с третьего и т.д. Т.е. средняя как бы «скользит» по ряду динамики с шагом равным 1.
Аналитическое выравнивание. Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда динамики выражаются в виде функции времени. 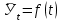
Выравнивание по среднегодовому абсолютному приросту основан на предположении, что каждый последующий уровень изменяется по сравнению с предыдущим приблизительно на одинаково величину, равную среднему абсолютному приросту. Уравнение, отражающие тенденцию развития имеет вид: 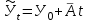 , ,
где 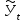 – выровненные уровни, отражающие тенденцию развития, – выровненные уровни, отражающие тенденцию развития,
У0 – начальный уровень ряда,
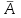 – средний абсолютный прирост, – средний абсолютный прирост,
t – порядковый номер даты (t = 0, 1, 2…n)
Литература:2, с. 141-189; 5 с. 246-273; 18, с. 103-155
Контрольные вопросы:
Что называют временным рядом?
Из каких основных элементов состоит временной ряд?
Дайте классификацию рядов динамики.
Назовите аналитические (абсолютные и относительные) показатели рядов динамики.
Какие способы выявления основной тенденции развития явлений Вы знаете?
Охарактеризуйте способы приведения рядов динамики к сопоставимому виду.
Тема 8 Индексы
Цель: Сформировать у студента систему знаний раскрывающих понятие индекс, его основных элементов, дать классификационную характеристику основных форм и видов индексов, раскрыть взаимосвязь индексов.
План:
1. Общее понятие об индексах и значение индексного метода анализа
2. Классификация индексов
3. Изучение взаимосвязи индексов
1. Общее понятие об индексах и значение индексного метода анализа
Индекс – относительный показатель, который получают при сопоставлении уровней сложных социально-экономических показателей для соизмерения их в пространстве, во времени и с планом.
В процессе развития индексной теории выделилось два направления:
Обобщающее или синтетическое 2. Аналитическое
Обобщающее или синтетическое направление трактует индекс как показатель среднего изменения уровня изучаемого показателя.
Аналитическое направление трактует индекс как показатель изменения уровня результативной величины под влиянием изменения показателя фактора.
С помощью индексных показателей решаются следующие основные задачи:
Характеристика общего изменения сложного экономического показателя или факторов, формирующих его отдельные показатели.
Изучение влияния показателя одного из факторов на результативные показатели путем исключения (элиминирования) влияния других факторов
Изучение влияния структуры явления на изменение индексируемой величины или на изменение результативного показателя.
2. Классификация индексов
Каждая индексируемая величина имеет свое символическое обозначение.
Индексируемая величина – величина, изменение которой изучается с помощью индекса.
q – количество единиц данного вида продукции в натуральную единицу измерения; p – цена единицы продукции данного вида; z – себестоимость единицы продукции; t – затраты труда на производство продукции (ч/дн, ч/час), 1-подстрочный символ текущего периода, 0- подстрочный символ базисного периода.
1) По степени охвата элементов совокупности различают индивидуальные и сводные (общие) индексы.
Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности (например, изменение выпуска легковых автомобилей определенной марки). Индивидуальные индексы обозначаются i.
Например, индивидуальный индекс цены: 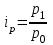 показывает изменение цены товара А в отчетном периоде по сравнению с базисным. показывает изменение цены товара А в отчетном периоде по сравнению с базисным.
 Сводный индекс отражает изменение по всей совокупности элементов сложного явления. Сводный индекс обозначается J. Сводный индекс состоит из: индексируемой величины, характер изменения которой определяется и соизмерителя, который называется весом. Сводный индекс отражает изменение по всей совокупности элементов сложного явления. Сводный индекс обозначается J. Сводный индекс состоит из: индексируемой величины, характер изменения которой определяется и соизмерителя, который называется весом.
Для исчисления сводных индексов необходимо привести составные части к сопоставимому виду.
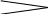 Например, сводный индекс цен Например, сводный индекс цен 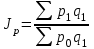 веса веса
Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные в текущем периоде товары. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились.
 Сводный индекс физического объёма товарооборота: Сводный индекс физического объёма товарооборота: 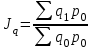 веса веса
Индексируемая величина – количество товаров в натуральном выражении. Его применение дает возможность оценить изменение физического объема продаж при сохранении цен неизменными. Цены в этом индексе фиксируются на уровне базисного периода.
2) По базе сравнения выделяют: динамические, территориальные индексы и индексы выполнения плана
Динамические индексы рассчитываются как базисным, так и цепным способами. Цепной способ – текущий уровень показателя сопоставляют с уровнем показателя за предшествующий период. При базисном способе текущий уровень показателя сопоставляют с уровнем показателя за базисный период.
Территориальные индексы характеризуют уровни сложных показателей, характеризующих различные территории или совокупности (одноименные показатели). Например, 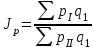 , где: р1 и p0 – цены на одни и те же товары в различных регионах. , где: р1 и p0 – цены на одни и те же товары в различных регионах.
Территориальные индексы выражают соотношение сложных экономических явлений в пространстве по городам, областям, районам, странам и т.д.
Индекс выполнения плана показывает изменение текущего уровня сложного показателя по сравнению с запланированным уровнем анализируемого показателя. 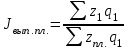 , ,
|
 Скачать 407.71 Kb.
Скачать 407.71 Kb.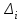 (или скорость роста)
(или скорость роста)
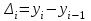
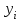 - уровень сравниваемого периода;
- уровень сравниваемого периода;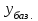 - уровень базисного периода;
- уровень базисного периода;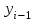 - уровень непосредственно предшествующего периода.
- уровень непосредственно предшествующего периода. 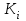
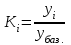
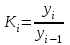
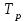
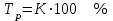
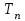 =
=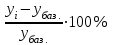
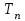 =
=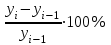
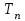 =
=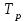 -100%
-100% 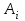
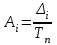 или
или 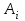 =
=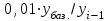
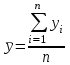
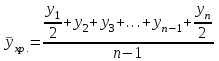 ,
,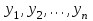 - уровни ряда в последовательные моменты времени.
- уровни ряда в последовательные моменты времени.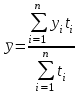 где
где 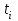 - количество дней (месяцев) между смежными датами.
- количество дней (месяцев) между смежными датами.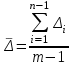 где n – число уровней ряда;
где n – число уровней ряда;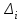 - абсолютные приросты по сравнению с предшествующим уровнем.
- абсолютные приросты по сравнению с предшествующим уровнем.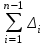 =
=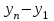 , тогда приведенную выше формулу можно преобразовать в следующий вид:
, тогда приведенную выше формулу можно преобразовать в следующий вид: 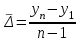
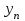 и
и 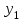 - соответственно конечный и начальный уровни динамического ряда.
- соответственно конечный и начальный уровни динамического ряда.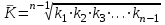 ,
,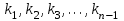 - коэффициенты роста по сравнению с уровнем предшествующего периода;
- коэффициенты роста по сравнению с уровнем предшествующего периода;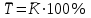
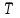 - средний годовой темп роста.
- средний годовой темп роста.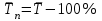
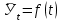
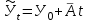 ,
,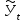 – выровненные уровни, отражающие тенденцию развития,
– выровненные уровни, отражающие тенденцию развития,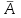 – средний абсолютный прирост,
– средний абсолютный прирост,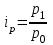 показывает изменение цены товара А в отчетном периоде по сравнению с базисным.
показывает изменение цены товара А в отчетном периоде по сравнению с базисным. Сводный индекс отражает изменение по всей совокупности элементов сложного явления. Сводный индекс обозначается J. Сводный индекс состоит из: индексируемой величины, характер изменения которой определяется и соизмерителя, который называется весом.
Сводный индекс отражает изменение по всей совокупности элементов сложного явления. Сводный индекс обозначается J. Сводный индекс состоит из: индексируемой величины, характер изменения которой определяется и соизмерителя, который называется весом.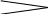 Например, сводный индекс цен
Например, сводный индекс цен 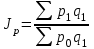 веса
веса  Сводный индекс физического объёма товарооборота:
Сводный индекс физического объёма товарооборота: 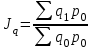 веса
веса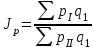 , где: р1 и p0 – цены на одни и те же товары в различных регионах.
, где: р1 и p0 – цены на одни и те же товары в различных регионах.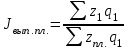 ,
,
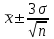 , где
, где  Различают начальные, начальные относительно
Различают начальные, начальные относительно 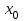 (условные), и центральные моменты. Начальные моменты
(условные), и центральные моменты. Начальные моменты 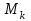 :
: 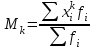 . Центральные моменты (
. Центральные моменты (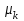 ):
): 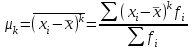 . Центральный момент
. Центральный момент 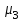 используется для числового измерения ассиметрии
используется для числового измерения ассиметрии 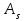 , которая определяется как отношение:
, которая определяется как отношение: 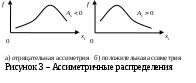
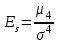 -3, которая характеризует островершинность или плосковершинность распределения, так называемую «крутость».
-3, которая характеризует островершинность или плосковершинность распределения, так называемую «крутость». 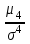 =3, таким образом
=3, таким образом 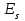 =0. Распределения более островершинные, чем нормальное, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом. На рис. 4 представлены островершинное (величина эксцесса положительная) и плосковершинное (величина эксцесса отрицательная) распределения.
=0. Распределения более островершинные, чем нормальное, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом. На рис. 4 представлены островершинное (величина эксцесса положительная) и плосковершинное (величина эксцесса отрицательная) распределения. 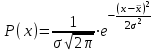 .
.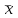 , средний размер в выборочной совокупности – выборочной средней, обозначаемой
, средний размер в выборочной совокупности – выборочной средней, обозначаемой 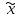 .
.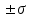 генеральной средней; 95,4% этой численности будет заключено в пределах
генеральной средней; 95,4% этой численности будет заключено в пределах 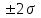 и 99,7% их не выйдет за пределы
и 99,7% их не выйдет за пределы 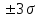 . Нормальное распределение имеет довольно общий характер и показывает частоту появления ошибок данного размера средней.
. Нормальное распределение имеет довольно общий характер и показывает частоту появления ошибок данного размера средней.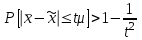 ,
,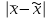 - абсолютная величина расхождения между генеральной средней и выборочной средней, составляющая ошибку репрезентативности;
- абсолютная величина расхождения между генеральной средней и выборочной средней, составляющая ошибку репрезентативности;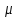 - среднее квадратическое отклонение вариантов выборочной средней от генеральной средней (средняя ошибка выборки). Оно зависит от колеблемости признака в генеральной совокупности
- среднее квадратическое отклонение вариантов выборочной средней от генеральной средней (средняя ошибка выборки). Оно зависит от колеблемости признака в генеральной совокупности 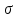 и числа отобранных единиц n:
и числа отобранных единиц n: 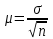 . Эта запись показывает, что о величине расхождения можно судить лишь с определенной вероятностью, которая зависит от коэффициента доверия t. Если выбратьt=2, то вероятность того, что это расхождение не превысит
. Эта запись показывает, что о величине расхождения можно судить лишь с определенной вероятностью, которая зависит от коэффициента доверия t. Если выбратьt=2, то вероятность того, что это расхождение не превысит 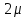 , будет не меньше чем 0,75, если t=3, то вероятность превысит 0,89 и т.д.
, будет не меньше чем 0,75, если t=3, то вероятность превысит 0,89 и т.д.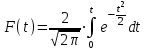
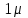 . Это может быть прочитано и так: с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превысит одной величины средней ошибки выборки. Другими словами, в 683 случаях из 1000 ошибка репрезентативности не выйдет за пределы
. Это может быть прочитано и так: с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превысит одной величины средней ошибки выборки. Другими словами, в 683 случаях из 1000 ошибка репрезентативности не выйдет за пределы 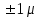 . С вероятностью 0,997 (довольно близкой к единице) можно ожидать, что разность между выборочной и генеральной средними не превзойдет трехкратной средней ошибки выборки.
. С вероятностью 0,997 (довольно близкой к единице) можно ожидать, что разность между выборочной и генеральной средними не превзойдет трехкратной средней ошибки выборки.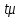 , обозначаемая
, обозначаемая 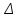 , называется предельной ошибкой выборки, которая определяется формулой
, называется предельной ошибкой выборки, которая определяется формулой 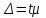 . С увеличением t увеличивается вероятность и величина ошибки.
. С увеличением t увеличивается вероятность и величина ошибки.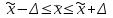
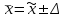
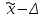 до
до 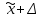 , то есть что доверительные интервал (
, то есть что доверительные интервал (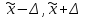 ) с заданной вероятностью заключает в себе генеральную среднюю.
) с заданной вероятностью заключает в себе генеральную среднюю.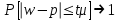
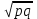 , где q=1–p, то средняя ошибка выборки для альтернативного признака выражается следующей формулой:
, где q=1–p, то средняя ошибка выборки для альтернативного признака выражается следующей формулой: 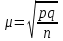
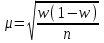
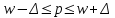 .
.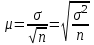
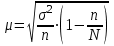
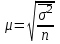 ; б) бесповторный отбор:
; б) бесповторный отбор: 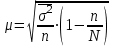 ,
, 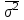 - средняя из внутригрупповых дисперсий в выборочной совокупности.
- средняя из внутригрупповых дисперсий в выборочной совокупности.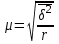 ; б) бесповторный отбор:
; б) бесповторный отбор: 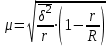 ,
, 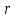 -
- 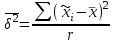
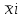 - групповые дисперсии,
- групповые дисперсии, 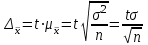
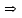
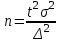
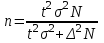 .
.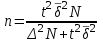 ,
,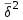 - средняя из внутригрупповых дисперсий,
- средняя из внутригрупповых дисперсий, 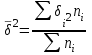 ,
, 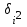 -групповые дисперсии
-групповые дисперсии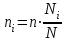 ;
;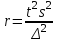
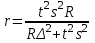 , где
, где 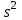 - межсерийная дисперсия Литература: 2; 5, с. 222-242; 18
- межсерийная дисперсия Литература: 2; 5, с. 222-242; 18