Шпаргалки к экзамену по теории вероятностей и статистике. шпоры ответы на вопросы к экзамену по твимс2. 1. Предмет теории вероятностей. Понятие случайного события
 Скачать 0.9 Mb.
|
|
15. Функция распределения и её свойства. Вероятность попадания случайной величины на заданный интервал. Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х: F (x) = p (X < x). (4.1) Свойства функции распределения. 0 ≤ F(x) ≤ 1. Действительно, так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность. Функция распределения является неубывающей функцией, то есть F(x2) ≥ F(x1) при х2 > x1. Это следует из того, что F(x2) = p(X < x2) = p(X < x1) + p(x1 ≤ X < x2) ≥ F(x1).  В частности, если все возможные значения Х лежат на интервале [a, b], то F(x) = 0 при х ≤ а и F(x) = 1 при х ≥ b. Действительно, X < a – событие невозможное, а X < b – достоверное. Вероятность того, что случайная величина примет значение из интервала [a, b], равна разности значений функции распределения на концах интервала: p ( a < X < b ) = F(b) – F(a). Если R — это непрерывная случайная величина, которая распределена равномерно в интервале (0, 1), а r — ее возможные значения, то вероятность попадания величины R (в результате испытания) в интервал (с, d), принадлежащий интервалу (0, 1), равна его длине:  В самом деле, плотность рассматриваемого равномерного распределения равна: а значит, вероятность попадания случайной величины R в интервал (с, d) будет: 20. Математическое ожидание и дисперсия числа появления события в независимых опытах. Математическое ожидание числа появления события в схеме независимых испытаний. Пусть производится n независимых опытов, вероятность появления события в каждом из которых равна Р. Число появлений события в этих n опытах является случайной величиною Х распределённой по биномиальному закону. Однако, непосредственное вычисление её среднего значения громоздко. Для упрощения воспользуемся разложением, которым будем пользоваться в дальнейшем неоднократно: Число появления события в n опытах состоит из числа появлений события в отдельных опытах, т.е.  где  имеет закон распределения (принимает значение 1, если событие в данном опыте произошло, и значение 0, если событие в данном опыте не появилось).
Поэтому  или  т.е. среднее число появлений события в n независимых опытах равно произведению числа опытов на вероятность 5 Дисперсия числа появления события в схеме независимых испытаний. Производится n независимых испытаний и вероятность появления события в каждом испытании равна р. Выразим, как и прежде, число появления события Х через число появления события в отдельных опытах  Так как опыты независимы, то и связанные с опытами случайные величины независимы. А в силу независимости имеем
Но каждая из случайных величин имеет закон распределения и  , поэтому по определению дисперсии ,где q=1-p В итоге имеем  ,  Среднее квадратическое отклонение числа появления событий в n независимых опытах равно  .17. Математическое ожидание случайной величины и его свойства.   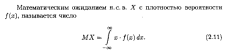   22. Закон равномерного распределения. Равномерный закон распределения. Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х)имеет следующий вид:  Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке. Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то  откуда с=1/(b-a). Теперь функцию f(x) можно представить в виде  Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:   : Графики функций f(x) и F(x) имеют вид:  Найдем числовые характеристики. Используя формулу для вычисления математического ожидания НСВ, имеем:  22. Таким образом, математическое ожидание случайной вели чины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка. Найдем дисперсию равномерно распределенной случайной величины  откуда сразу же следует, что среднее квадратическое отклонение:  Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку [a, b]: 
Геометрически эта вероятность представляет собой площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение. 23. Экспонентный закон распределения. 24. Нормальное распределение. Функция Лапласа. Вероятность попадания в заданный интервал. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности  Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.  Обозначим  Тогда  Т.к. интеграл  не выражается через элементарные функции, то вводится в рассмотрение функция которая называется функцией Лапласа или интегралом вероятностей. Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах. Ниже показан график функции Лапласа. 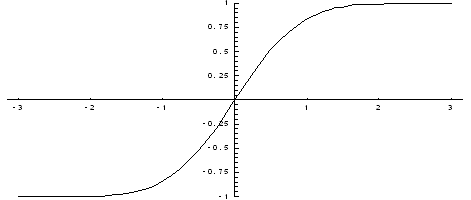 Функция Лапласа обладает следующими свойствами: 1) Ф(0) = 0; 2) Ф(-х) = - Ф(х); 3) Ф(¥) = 1. Функцию Лапласа также называют функцией ошибок и обозначают erf x. Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:  Ниже показан график нормированной функции Лапласа. 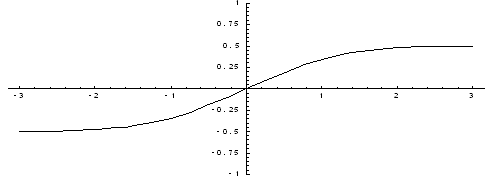 23. Экспонентный закон распределения. Определение. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром  , если её плотность вероятности f(x) имеет вид: Кривая распределения f(x) приведена на рисунке  Теорема. Функция распределения случайной величины X, распределённой по показательному закону, есть  её математическое ожидание  а её дисперсия  Доказательство. График функции распределения F(x) случайной величины X, имеющей показательное распределение представлен на рисунке 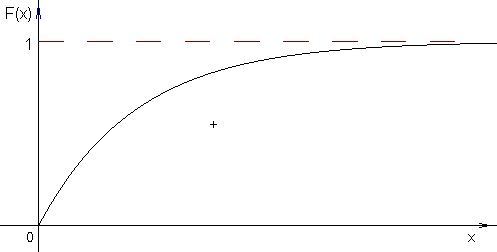 Следствие. Для случайной величины, распределённой по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т. е.  Показательный закон распределения играет большую роль в теории массового обслуживания и теории надёжности. Так, например, интервал времени Т между двумя соседними событиями в простейшем потоке событий имеет 26. Плотность распределения вероятностей двумерной случайной величины и её свойства. Вероятность попадания случайной точки в произвольную область. Пусть в плоскости Оху задана произвольная область D. Найдем вероятность того, что точка, координаты которой представляют собой систему двух случайных величин (двумерную случайную величину) с плотностью распределения f(x, y), попадет в область D. Разобьем эту область прямыми, параллельными осям координат, на прямоугольники со сторонами Δх и Δу. Вероятность попадания в каждый такой прямоугольник равна  , где  - координаты точки, принадлежащей прямоугольнику. Тогда вероятность попадания точки в область D есть предел интегральной суммы  , то есть (8.3)Отыскание плотностей вероятности составляющих двумерной случайной величины. Выше было сказано, как найти функцию распределения каждой составляющей, зная двумерную функцию распределения. Тогда по определению плотности распределения  (8.4)Аналогично находится  (8.4′)25. Функция распределения двумерной случайной величины. Определение 8.1. Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y: F( х, у ) = p ( X < x, Y < y ).  Рис.1.Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у). Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины. Свойства функции распределения. 0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью). F(x, y) есть неубывающая функция по каждому аргументу: F(x2, y) ≥ F(x1, y), если x2 > x1; F(x, y2) ≥ F(x, y1), если y2 > y1. Доказательство. F(x2, y) = p(X < x2, Y < y) = p(X < x1, Y < y) + p(x1 ≤ X < x2, Y < y) ≥ ≥ p(X < x1, Y < y) = F(x1, y). Аналогично доказывается и второе утверждение. Имеют место предельные соотношения: а) F(-∞, y) = 0; b) F(x, - ∞) = 0; c) F(- ∞, -∞) = 0; d) F( ∞, ∞) = 1. Доказательство. События а), b) и с) невозможны ( так как невозможно событие Х<- ∞ или Y <- ∞), а событие d) достоверно, откуда следует справедливость приведенных равенств. При у = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Х: F(x, ∞) = F1(x). При х = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Y : F( ∞, y) = F2(y). Доказательство. Так как событие Y < ∞ достоверно, то F(x, ∞) = р(Х < x) = F1(x). Аналогично доказывается второе утверждение. 31. Центральная предельная теорема. Рассмотрим одну из наиболее общих форм центральной предельной теоремы: Пусть имеется взвешенная сумма независимых случайных непрерывных величин x1, x2, x3, …., xn с произвольными законами распределения:  , где  постоянная, фиксированная числа.Пусть i-ая случайная величина имеет  и  (i=1,2,3,…,n-1,n)Согласно теореме о числовых характеристиках случайных величин, получим:   Центральная предельная теорема утверждает, что при достаточно общих условиях распределения суммарной Yn при  стремиться к нормальному распределению   |
