практическая производные. доклад 1 производные. 1 производные уравнение нормали касательной и графиков функций с формулами
 Скачать 77.74 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Саратовский государственный технический университет имени Гагарина Ю.А.» (СГТУ имени Гагарина Ю.А.) ПРОФЕССИОНАЛЬНО-ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ Доклад на тему: «1 производные уравнение нормали касательной и графиков функций с формулами» По дисциплине: «Математика» Выполнил: студент 1 курса Группы САД-912 Шаламов Иван Андреевич Проверил: преподаватель Рахманина Инесса Юрьевна Саратов, 2022 Как получить уравнение касательной и уравнение нормали Касательная - это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной. Уравнение касательной выводится из уравнения прямой. Выведем уравнение касательной, а затем - уравнение нормали к графику функции. Вспомним уравнение прямой с угловым коэффициентом: y = kx + b. В нём k - угловой коэффициент. Отсюда получаем следующую запись: y - y0 = k(x - x0). Значение производной f '(x0) функции y = f(x) в точке x0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M0(x0, y0), где y0 = f(x0). В этом состоит геометрический смысл производной. Таким образом, можем заменить k на f '(x0) и получить следующее уравнение касательной к графику функции: y - y0 = f '(x0)(x - x0). В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль. Теперь об уравнении нормали. Нормаль - это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали: (x - x0) + f '(x0)(y - y0) = 0 Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне). Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет "холодным душем". Пример 0. Составить уравнение касательной и уравнение нормали к графику функции  в точке M (1, 1).Правильное решение и ответ. Решаем задачи вместе Пример 1. Составить уравнение касательной и уравнение нормали к графику функции  , если абсцисса точки касания  .Решение. Найдём ординату точки касания:  .Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):  .Найдём значение производной в точке касания, то есть угловой коэффициент касательной:  .Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем  В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:  На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета. 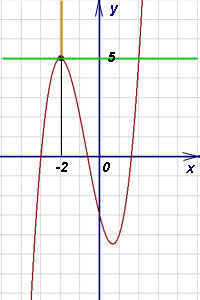 Следующий пример - тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг - приведение уравнения к общему виду. Пример 2. Составить уравнение касательной и уравнение нормали к графику функции  , если абсцисса точки касания  .Решение. Найдём ординату точки касания:  .Найдём производную функции:  .Найдём значение производной в точке касания, то есть угловой коэффициент касательной:  .Подставляем все полученные данные в "формулу-болванку" и получаем уравнение касательной:  Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):  Составляем уравнение нормали: 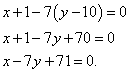 Пример 3. Составить уравнение касательной и уравнение нормали к графику функции  , если абсцисса точки касания  .Решение. Найдём ординату точки касания:  .Найдём производную функции (по формуле 5 в таблице производных):  .Найдём значение производной в точке касания, то есть угловой коэффициент касательной:  .Находим уравнение касательной: 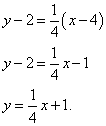 Перед тем, как привести уравнение к общему виду, нужно его немного "причесать": умножить почленно на 4. Делаем это и приводим уравнение к общему виду:  Составляем уравнение нормали: 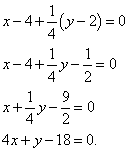 Нет времени вникать в решение? Можно заказать работу! Решить задачи самостоятельно, а затем посмотреть решения Пример 4. Составить уравнение касательной и уравнение нормали к графику функции  , если абсцисса точки касания  .Правильное решение и ответ. Пример 5. Составить уравнение касательной и уравнение нормали к графику функции  , если абсцисса точки касания  .Правильное решение и ответ. Снова решаем задачи вместе Пример 6. Составить уравнение касательной и уравнение нормали к графику функции  , если абсцисса точки касания  .Решение. Найдём ординату точки касания:  .Найдём производную функции (по формуле 14 в таблице производных):  .Найдём значение производной в точке касания, то есть угловой коэффициент касательной:  .Получаем уравнение касательной:  Приводим уравнение к общему виду:  Составляем уравнение нормали:  Распространённая ошибка при составлении уравнений касательной и нормали - не заметить, что функция, данная в примере, - сложная и вычислять её производную как производную простой функции. Следующие примеры - уже со сложными функциями (соответствующий урок откроется в новом окне). Пример 7. Составить уравнение касательной и уравнение нормали к графику функции  , если абсцисса точки касания  .Решение. Найдём ординату точки касания:  .Внимание! Данная функция - сложная, так как аргумент тангенса (2x) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции): 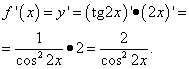 .Найдём значение производной в точке касания, то есть угловой коэффициент касательной:  .Получаем уравнение касательной:  Приводим уравнение к общему виду:  Составляем уравнение нормали:  Пример 8. Составить уравнение касательной и уравнение нормали к графику функции  , если абсцисса точки касания .Решение. Найдём ординату точки касания:  .Как и в предыдущем примере, данная функция - сложная, так как степень (  ) сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции): .Найдём значение производной в точке касания, то есть угловой коэффициент касательной:  .Получаем уравнение касательной:  Приводим уравнение к общему виду:  Составляем уравнение нормали: 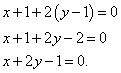 |