контр р по проф обуч номер 2. 1. Расчет длительности производственного цикла
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
Тема 4 . Основы сетевого планирования и управления Система СПУ представляет собой разновидность оперативно-производственного планирования, обеспечивающую динамическое планирование, управление ходом комплекса работ, необходимых для выполнения общего задания. Эти методы позволяют оптимизировать процесс создания новой техники: а) по времени (обеспечить минимальную длительность цикла); б) по стоимости (обеспечить минимум затрат). Особенности системы СПУ: 1. Возможность рассматривать в динамике объект проектируемого управления. 2. Возможность выделить на каждом этапе выполнения общего задания наиболее важные решающие участки работ, на которых в данный момент времени должны быть сосредоточены финансовые, материальные и трудовые ресурсы. 3. Объективность (система не допускает субъективных моментов в управлении ходом работ). 4. Наглядность (сетевой график является графическим изображением комплекса работ). 5. Возможность успешно применять математические методы и ЭВМ, которые придают системе большую оперативность. 6. Системность СПУ, которая выражается в организации центрального органа, руководящего всем комплексом работ, в исполнении которых могут участвовать различные соисполнители. 7. Возможность постоянной оптимизации как при планировании, так и при проведении работ. 8. Универсальность (система может применяться для целого комплекса решаемых задач: в области планирования предприятия, проектирования строительства, при проведении научно-исследовательских работ при организации технической подготовки производства и т.д.). Элементы сетевого графика Сетевой график является полной графической моделью комплекса работ, в котором определяется последовательность и взаимосвязь между ними. Важнейшими элементами сетевого графика являются события и работы. Понятие «работа» (это процесс, который протекает во времени) используется в широком смысле и имеет следующие значения: 1. Действительная работа – трудовой процесс, требующий затрат времени и ресурсов (составление программы для ЭВМ). 2. Ожидание – процесс, требующий затрат времени, но не требующий затрат ресурсов (трудовых, материальных, финансовых). 3. Фиктивная работа – логическая связь между работами, не связана с расходом времени и ресурсами (ждем подписи на делах). Эта логическая связь указывает на то, что одна работа зависит от другой и не начнется раньше, чем та закончится. Работа на графике обозначается в виде прямой со стрелкой, фиктивная работа – пунктирной стрелкой:  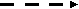 Понятие «событие» имеет следующие значения: 1. Исходное событие – начало выполнения проекта, оно не имеет предшествующих работ (одно на всем графике, нет входящих стрелок):  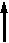 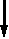  2. Завершающее событие – достижение конечной цели проекта, оно не имеет следующих за ним работ (нет выходных стрелок): 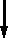    3. Промежуточное событие – или просто событие – результат одной работы или совокупный результат нескольких работ. 4. Начальное событие – непосредственно начинает данную работу. Для каждой работы – единственное. Их столько на графике, сколько работ.     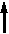 5  . Конечное событие - завершает данную работу. . Конечное событие - завершает данную работу.События на графике обозначаются кружками: 5 В   11 2 сякая работа соединяет два события:  Всем событиям присваивается определенный номер (цифровой код), т.е. всякая работа может быть закодирована номерами ее начального и конечного событий. Продолжительность выполнения работы измеряется в единицах времени (могут быть материальные ресурсы, трудоёмкость). Каждая работа должна иметь определение, раскрывающее её содержание. Событие, не имеющее продолжительности, не является процессом. Наступление события соответствует моменту окончания последней из работ, непосредственно предшествующей данному событию. Правила построения сетевых графиков При построении сетевых графиков необходимо учитывать следующее: 1. Сеть всегда вычерчивается слева направо. Поэтому каждое событие с большим порядковым номером изображается правее предыдущего. 2. Два соседних события могут соединяться лишь одной ра-ботой. 3. Каждая работа должна быть заключена между двумя событиями; при этом нельзя допускать различных работ, имеющих одинаковые коды (а). В подобных случаях в сеть должны быть введены дополнительные события и фиктивные работы (б). 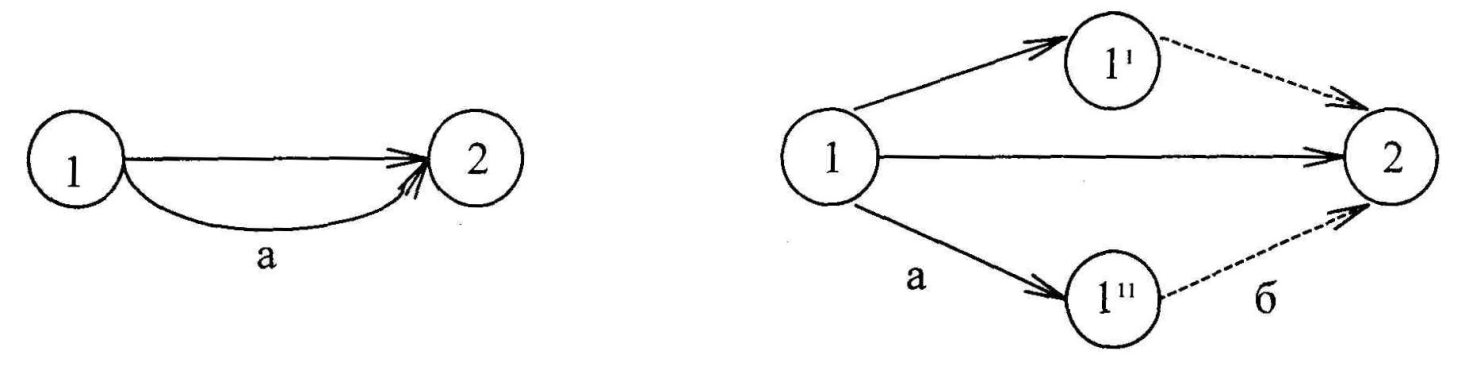 4. В сети нельзя допускать «тупиков», т.е. промежуточных событий, из которых не следует ни одной работы, если эти события не являются для данной сети завершающими. Наличие «тупиков» в сети указывает либо на ошибку, либо на то, что результат работ, непосредственно предшествующих этому событию, никому из исполнителей данного проекта не нужен. Следовательно, такие работы можно исключить. 5. В сети не должно быть событий, за исключением исходного, в которое не входит ни одной работы. Наличие таких событий в сети также говорит об ошибке либо о том, что результат, необходимый одному из исполнителей данного проекта в качестве исходных условий для начала выполняемой им работы, никому не задан и следующее данное событие не может наступить. При обнаружении такого события необходимо найти исполнителей работ, обеспечивающих достижение данного результата и включить эти работы в сеть. 6. В сети не должно быть замкнутых контуров, т.е. путей, соединяющих некоторое событие с ним же самим.         1 2 3 При обнаружении подобной ошибки сеть после соответствующей проверки необходимо исправить. 7. Следует стремиться к тому, чтобы стрелки работы на исходном графике по возможности не пересекались. Избегать этого можно либо смещая событие, либо изображая стрелки в виде дуг или ломаных линий. Если исходный график не удовлетворяет требованиям, он считается неупорядоченным и его следует упорядочить. Расчет параметров сетевого графика Любая последовательность работ в сети, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы, называется путём. (Полный путь – последовательность работ и событий между исходным и завершающим событиями. Неполный путь – последовательность работ и событий между исходным событием и какими-либо промежутками или между двумя промежутками). Если известна продолжительность выполнения каждой работы, то для каждого пути может быть определена его продолжительность. Продолжительность любого пути равна сумме продолжительностей составляющих его работ. Путь, имеющий наибольшую продолжительность, называется критическим – Zкр., его продолжительность – Ткр.. Продолжительность критического пути определяет общую продолжительность выполнения проекта в целом. Следовательно, чтобы сократить сроки выполнения проекта, необходимо сократить сроки выполнения работ, находящихся на критическом пути. Критический путь на графике выделяется жирными стрелками. Ранний срок наступления любого события tр(i) равен наибольшему по продолжительности пути, предшествующему этому событию. Поздний срок наступления события tп(i) равен разности между Ткр. и продолжительностью наиболее длинного пути, следующего за событием i. Z1(i) - наибольший по продолжительности путь, предшествующий событию i. Z2(i) - наибольший по продолжительности путь, следующий за событием i. tр(i)=t[Z1(i)]. tп.(i)=Tкр.-t[Z2(i)]. Для событий, принадлежащих критическому пути: tp.(i)=tп.(i), т. к. Z1(i)+Z2(i)=Tкр. Ранний срок начала работы tp.н.(ij): tp.н.(ij)= tp.(i). Поздний срок начала работы tп.н.(ij): tп.н.(ij)= tп.(j)-t(ij). Ранний срок окончания работы tp.о.(ij): tp.о.(ij)= tp.(i)+ t(ij). Поздний срок окончания работы tп.о.(ij): tп.о.(ij)= tп.(j). Для всех работ критического пути: tp.н.(ij)= tп.н.(ij). tp.о.(ij)= tп.о.(ij). Разность между продолжительностью критического пути и продолжительностью пути называется резервом времени пути Z и обозначается через R(Z). R(Z)= Ткр.-t(Z). Чем короче путь, тем больше у него резерв времени. R(Z) показывает, на сколько в сумме могут быть увеличены продолжительности работ, принадлежащих пути Z, не влияя на срок выполнения проекта, т.е. R(Z) показывает предельно допустимое увеличение продолжительности пути Z. Поскольку резерв времени пути Z может быть использован для увеличения продолжительности работ, находящихся на этом пути, можно утверждать, что любые из работ пути Z на его участке, не совпадающем с критическим путем, обладают резервом времени. Работа (ij) может принадлежать нескольким путям, у которых продолжительность и резервы разные. Поэтому для работ определяют два основных резерва времени – полный и свободный. Полный резерв времени работы Rп(ij) равен разности между поздним сроком наступления события j и ранним сроком наступления события i с вычетом продолжительности работы (ij): Rп(ij)=tп.(j)-tр.(i)-t(ij). Полный резерв времени работы показывает, насколько может быть увеличена продолжительность отдельной работы или отсрочено её начало, чтобы продолжительность проходящего через неё максимального пути не превысила продолжительности критического пути. Полный резерв времени работ, лежащих на критическом пути, равен нулю; для остальных он больше нуля. Свободный резерв времени работы Rc(ij) равен разности между ранними сроками наступления событий (i,j) за вычетом продолжительности работы (ij): Rс(ij)=tр.(j)-tр.(i)-t(ij). Свободный резерв времени работы – это максимальное время, на которое можно увеличить продолжительность отдельной работы или отсрочить её начало без изменения ранних сроков начала последующих работ. Для работ, лежащих на критическом пути, свободный резерв времени равен нулю. Свободный резерв может быть равен нулю и для работ, не лежащих на критическом пути. Все события в сети, за исключением событий, принадлежащих критическому пути, имеют резервы времени. Резерв времени наступления события R(i) определяется как разность между поздним и ранним сроками наступления данного события: R(i)=tп.(i)-tр.(i). Резерв времени наступления события показывает, на какой предельно допустимый срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения проекта. События критического пути не имеют резервов времени, т.к. tп.(i)=tр.(i). Оптимизация сетевых графиков Зная временные параметры графика, можно более целенаправленно маневрировать трудовыми, материальными и финансовыми ресурсами, обращая внимание прежде всего на работы, лежащие на критическом пути, а также на путях, близких по продолжительности к критическому (подкритические пути). После составления исходного графика приступают к его оптимизации (корректировке), т.е. приведению его в соответствие с заданными (директивными) сроками и имеющимися ресурсами (денежными, материальными и т.д.). Первоначально сетевой график корректируется во времени без учёта ограничений. Эта работа заключается в основном в сокращении сроков выполнения поставленной задачи (длительности критического пути). Для успешного выполнения всего комплекса работ недостаточно чёткой координации во времени. Необходимо также учитывать материальные, трудовые и финансовые ресурсы, т.е. все ограничения, наложенные на выполнение задания. Корректировка по времени с учетом ограничений заключается в следующем: 1) Пересмотр технологии сети, т.е. изменение состава и последовательности выполняемых работ, а также взаимосвязь между ними, замена последовательного выполнения работ на параллельный. 2) Сокращение продолжительности отдельных работ, лежащих на критическом и подкритическом путях; это возможно выполнить за счет перераспределения или привлечения дополнительных ресурсов, а также за счет улучшения организации и технологии проведения этих работ. 3) Варьирование сроков выполнения остальных работ в пределах имеющихся у них резервов времени с целью лучшего использования ресурсов. Оптимизация по времени проводится до тех пор, пока не получится вариант, укладывающийся в заданные директивные сроки. Управление заключается в непрерывном наблюдении за ходом работ на основе получаемой от исполнителей информации. Наблюдение ведется в основном за работами, лежащими на критическом и подкритическом путях. Наблюдение необходимо для успешного выполнения всего комплекса работ в срок и координации работы всех исполнителей. На основе полученных данных после внесения их в график работы производится анализ сети с целью выявления отставаний и путей их ликвидации. Система СПУ позволяет заранее предвидеть отклонения и принять все необходимые меры для досрочного выполнения всего комплекса работ. Задачи 4.1. Рассчитать основные параметры сетевого графика ремонта технологического оборудования:  Решение (параметры для работы 4.6): 1. Определяем пути сетевого графика: λ1 (1,2,5,7); λ2 (1,2,4,7); λ3 (1,2,4,6,7); λ4 (1,3,6,7); λ5 (1,2,3,6,7). 2. Определяем продолжительность путей и выявляем критический путь: t(λ1)=4+2+2=8 дней; t(λ2)=4+3+3=10 дней; t(λ3)=4+3+1+1=9 дней; t(λ4)=1+2+1=4 дня; t(λ5)=4+1+2+1=8 дней. Критическим путем является второй путь, равный 10 дням (т.е. для выполнения комплекса работ по ремонту оборудования потребуется 10 дней). 3. Определяем ранний и поздний сроки наступления события (6): tp.(6)=t[Z1(6)]=4+3+1=8 дней (=max путь до 6); tп.(6)=Ткр.-t[Z2(6)]=10-1=9 дней (Ткр.- max путь от 6 до 7). 4. Определяем ранний и поздний сроки начала и окончания работы (4,6): tp.н.(4,6)=tp.(4)=4+3=7 дней { tp.(i)}; tп.н.(4,6)=tп.(6)-t(4,6)=9-1=8 дней {tп.(j)-t(ij)}; tр.о.(4,6)=tр.(4)+t(4,6)=7+1=8 дней {tр.(i)+t(ij)}; tп.о.(4,6)=tп.(6)=9 дней { tп.(j)}. 5. Определяем резерв времени путей, проходящих через событие (6): R(Z)=Ткр.-t(λ). Через событие (6) проходят следующие пути: λ1 (1,3,6,7); λ2 (1,2,4,6,7); λ3 (1,2,3,6,7). t(λ1)=1+2+1=4 дня R(λ1)=10-4=6 дней t(λ2)=4+3+1+1=9 дней R(λ2)=10-9=1 день t(λ3)=4+1+2+1=8 дней R(λ3)=10-8=2 дня 6. Рассчитываем полный резерв времени работы (4,6): Rп.(4,6)=tп.(6)-tр.(4)-t(4,6)=9-7-1=1 день. 7. Определяем свободный резерв времени работы (4,6): Rс.(4,6)=tр.(6)-tр.(4)-t(4,6)=8-7-1=0 дней. 8. Рассчитываем резерв времени наступления события (6): R(6)=tп.(6)-tр.(6)=9-8=1 день. tп.(i)-tр.(i). 4.2. Построить фрагмент сети при следующих условиях: работы А, Б, В, Г выполняются последовательно, причем для начала работы В необходим результат Б, а работа Г может начинаться после получения результата работы В. 4.3. Построить график выполнения работ А, Б, В, Г и Д, применив сетевую модель при следующих условиях:
4.4. Построить фрагмент сети при следующих данных из шести работ А, Б, В, Г, Д, Е. Работы А, Б, В начинаются одновременно после свершения начального события. Для начала работы Г необходимы результаты работ А и Б; для начала работы Д необходим только результат работы Б, а для начала работы Е необходимы результаты работ Б и В. 4.5. Построить фрагмент сети при следующих условиях: после окончания работы А начинают выполняться одновременно три работы Б, В, Г, после окончания которых выполняются ёще три работы Д, Е, Ж. Для начала работы Ж необходим результат работ В и Г, а для начала работы Д необходимы результаты всех трех работ Б, В, Г. 4.6. За исполнителем закреплено пять работ: А, Б, В, Г и Д. начало работ обусловлено следующими зависимостями:
Построить график выполнения работ. 4.7. Построить фрагмент сети при следующих условиях: выполняется комплекс, состоящий из восьми работ А, Б, В, Г, Д, Е, Ж, З. Известно, что работы Б, В, Г начинаются одновременно после окончания работы А; работа Е выполняется после окончания работы Б; а работа Д выполняется после окончания работы Г. Для начала работы З необходимы результаты работ Е, В, Д; а для начала работы Ж необходим результат работы Д. 4.8. Построить график выполнения работ А, Б, В, Г, применив сетевую модель, при следующей взаимосвязи этих работ:
|
