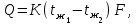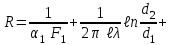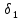1. Тема_ Теплопроводность и теплопередача_заоч. 1 Расчет стационарной теплопроводности и теплопередачи
 Скачать 420.68 Kb. Скачать 420.68 Kb.
|
|
1.1. Расчет стационарной теплопроводности и теплопередачи С теоретическими основами по данной теме следует познакомиться по учебнику [4], с. 22-38. Обратите внимание на обозначение и размерность передаваемой теплоты: Q, Дж – количество теплоты, передаваемое через изотермическую поверхность F, м2 за промежуток времени , с; Q, Вт – тепловой поток (теплота, передаваемая через изотермическую поверхность F за время = 1 с); q, Вт/м2 - плотность теплового потока (теплота, передаваемая через F=1м2 за время = 1с;  - линейная плотность теплового потока (теплота, передаваемая через стенку трубы длиной ℓ = 1м за время = 1 с). - линейная плотность теплового потока (теплота, передаваемая через стенку трубы длиной ℓ = 1м за время = 1 с).В табл. 1. приведены формулы для расчета теплопроводности и теплопередачи плоских и цилиндрических стенок. Таблица 1
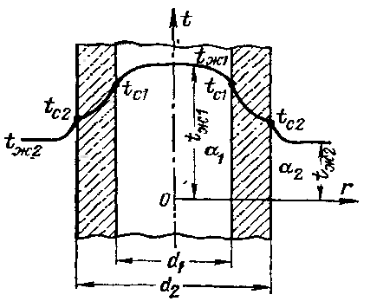
Теплопередача через стенки Дано  , граничные условия третьего рода. , граничные условия третьего рода.   - частные термические сопротивления - частные термические сопротивления Многослойная плоская стенка   Цилиндрическая стенка 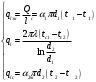 решим относительно решим относительно 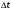  ; ;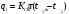 ; ; ; ; - линейное термическое сопротивление. - линейное термическое сопротивление.Многослойная стенка  = = . .Если стенка тонкая,  = = , , -средний диаметр стенки, -средний диаметр стенки, 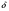 -толщина, K - для плоской стенки. -толщина, K - для плоской стенки.Задачи для самостоятельного решения № 1. Через кирпичную стену передается теплота. Известны постоянные температуры на поверхностях стены t1=20оС и t2 = -10оС, коэффициент теплопроводности кирпича =0,14  , толщина стены =40 см, площадь изотермической поверхности F=15 м2. , толщина стены =40 см, площадь изотермической поверхности F=15 м2.Рассчитать: плотность теплового потока (q, Вт/м2), теплоту, переданную через стену за сутки (Q, Дж), координату изотермической поверхности (х0) с температурой t=0оС. Ответы выделить. Изобразить схематично график распределения температур по толщине стены. № 2. Теплота передается через стенку трубы толщиной =50мм. Известны постоянные температуры на внутренней поверхности трубы t1= 100оС и на наружной t2=80 оС, а также коэффициент теплопроводности стенки =0,2  , внутренний диаметр d1 =50 мм и длина трубы , внутренний диаметр d1 =50 мм и длина трубы 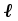 =10 м. =10 м.Рассчитать: линейную плотность теплового потока (q, Вт/м); количество теплоты, передаваемой через стенку трубы за одни сутки (Q, Дж); температуру изотермической поверхности в середине стенки трубы (t), т.е. при  . Сравнить полученную температуру с . Сравнить полученную температуру с  , объяснить причину несовпадения температур t и tср, показать t и tср на графике распределения температур по толщине стенки. , объяснить причину несовпадения температур t и tср, показать t и tср на графике распределения температур по толщине стенки.№ 3. Теплота передается через плоскую стальную стенку с коэффициентом теплопроводности с=40 Вт/мК от дымовых газов к кипящей воде. Толщина стенки с=25 мм, температура дымовых газов tж1=1200оС, температура воды tж2=180оС, коэффициент теплоотдачи от газов к стенке 1=30 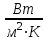 и от стенки к воде 2=4000 и от стенки к воде 2=4000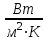 . .Определить: коэффициент теплопередачи (К, Вт/м2 К) от газов к воде; плотность теплового потока, передаваемого через стенку (q, Вт/м2); температуры на поверхностях стенки со стороны газов (t1) и со стороны воды (t2). Построить график распределения температур по толщине стенки. Нанести на график температуры tж1 и tж2. В процессе эксплуатации стенка со стороны воды покрылась слоем накипи толщиной н= 1,4 мм, коэффициент теплопроводности накипи н=1,0 Вт/мК. Рассчитать для этого случая К, q, t1, t2, температуру на поверхности накипи (tн). Построить график распределения температур по толщине стенки и накипи. Дать сравнительный анализ двух графиков. № 4. Теплота передается через стенку стальной трубы толщиной с=3мм с=50 Вт/м·К от дымовых газов к кипящей воде. Известны внутренний диаметр трубы d1=0,05 м, температура дымовых газов tж1=1200оС, температура кипящей воды tж2=180оС, коэффициент теплоотдачи от дымовых газов к наружной поверхности трубы 1=70 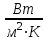 , коэффициент теплоотдачи от внутренней поверхности трубы к воде 2 =4000 , коэффициент теплоотдачи от внутренней поверхности трубы к воде 2 =4000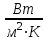 . .Рассчитать: коэффициент теплопередачи (К, Вт/ м2 · К) от газов к воде; линейную плотность теплового потока (q, Вт/м); температуры на внутренней поверхности трубы (t1) и на наружной поверхности (t2). Построить график распределения температур по толщине стенки. Нанести на график температуры t ж1 и t ж2. В процессе эксплуатации на внутренней поверхности образовался слой накипи толщиной (н=1,4 мм). Рассчитать для этого случая К, q,, t1, t2, температуру на поверхности накипи (tн). Принять коэффициент теплопроводности накипи н=0,8 Вт/м·К. Построить график распределения температур по толщине стенки и накипи. Дать сравнительный анализ двух графиков. № 5. По стальному теплоизолированному трубопроводу, расположенному на открытом воздухе, передается горячий теплоноситель. Толщина стенки трубы =3 мм, коэффициент теплопроводности стали =50 Вт/м·К. Температура окружающего воздуха tж=20оС, коэффициент теплоотдачи от поверхности изоляции к окружающему воздуху =10 Вт/м2К, внутренний диаметр трубы d1=150 мм, температура на внутренней поверхности стальной трубы t1=180оС, толщина слоя изоляции из=40 мм и коэффициент теплопроводности изоляции из=0,07  . .Рассчитать: температуру на поверхности изоляции (tиз), температуру наружной поверхности стальной трубы (t2), суточную потерю тепла на участке трубы длиной 100м (Q, Дж). Ответы выделить. Изобразить схематически график распределения температур по толщине стенки трубы и по толщине изоляции. Методические указания к решению задач №1-5 П  ри расчетах теплопроводности через плоскую стенку с постоянными температурами на поверхностях (t1 и t2) температуру (t) на любой координате х (0 При расчетах одномерной теплопередачи через многослойную стенку любой формы (плоская, цилиндрическая и т.д.) следует учитывать, что тепловой поток, передаваемый через многослойную стенку, проходит через каждый слой, и температуры на границе слоев определяются этим потоком. Т Рис. 1ак, для трехслойной плоской стенки(рис. 1) с исходными данными: 1, 2, 3, λ1, λ2, λ3, tж1, tж2, 1, 2, F тепловой поток Q может быть вычислен по формуле  где  - термические сопротивления, обусловливающие перепады температур tж1 – t1, t1 – t2 и т. д. - термические сопротивления, обусловливающие перепады температур tж1 – t1, t1 – t2 и т. д.Для нахождения температур t1, t2, t3, t4 можно использовать любые формулы из приведенных ниже: 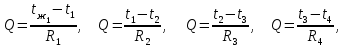  и т. д. и т. д.При построении графиков распределения температур в качестве образца может служить схемы из табл. 1, рис. 1. № 6. Определить толщину тепловой изоляции б, выполненной из: 1) альфоля и 2) шлаковой ваты. Удельные потери теплоты через изоляционный слой q=523 вт/м2, температуры его поверхностей tWl = 700° и tW2 = 40o С. Коэффициент теплопроводности альфоля при толщине воздушных слоев 10 мм λ= 0,0302 + 0,000085 t и коэффициент теплопроводности шлаковой ваты λ= 0,058 + + 0,000145 t. № 7.  Определить количество теплоты, проходящее через единицу длины стенки камеры сгорания ЖРД диаметром d=180мм, если толщина стенки бW = 2,5 мм, коэффициент теплопроводности материала из хромоникелевой стали марки 1ХГ8Н9Т λ = 34,9 вт/(м-град). Температуры на поверхностях стенке поддерживаются постоянными и равными tWl =4200° и tW2= 600° С. Определить количество теплоты, проходящее через единицу длины стенки камеры сгорания ЖРД диаметром d=180мм, если толщина стенки бW = 2,5 мм, коэффициент теплопроводности материала из хромоникелевой стали марки 1ХГ8Н9Т λ = 34,9 вт/(м-град). Температуры на поверхностях стенке поддерживаются постоянными и равными tWl =4200° и tW2= 600° С. № 8. Для условий задачи 7 определить количество теплоты, прошедшее через единицу длины стенки камеры сгорания ЖРД с защитным покрытием толщиной бп = 0,5 мм и его коэффициентом теплопроводности λ п = 2,67 вт /(м- град). № 9. Определить температуры на поверхностях соприкосновения слоев стенки tW2 камеры сгорания ЖРД и на внешней поверхности twз (рис. 14-1), если диаметр камеры d=190 мм, толщина защитного покрытия бп =1 мм и его коэффициент теплопроводности λ п =1,15 вт/(м-град), а толщина основной стенки 8W=2мм и ее коэффициент теплопроводности λW = 372 вт/(м-град) . Удельный тепловой поток q = 407 500 вт/м2, температура на поверхности покрытия со стороны камеры tWl = 1200° С. № 10. Определить удельный тепловой поток, проходящий через стенку рабочей лопатки газовой турбины, если средние температуры на поверхностях стенки соответственно равны tWl = 650° С и tw2 =630° С; толщина стенки лопатки бw = 2,5 мм и λW = 23,85 вт/(м-град). № 11. Определить удельный тепловой поток с учетом и без учета теплового сопротивления контакта через многослойную плоскую стенку, состоящую из слоя окиси циркония толщиной б1 = 0,2 мм, слоя стали толщиной б2 = 6 мм и слоя алюминия толщиной б3 = 10 мм (рис. 14.2), если температуры на внешних поверхностях стенки поддерживаются постоянными и равными tWl = 1200° С и tW4 = 400° С; коэффициент теплопроводности окиси циркония λ1 = l,15 Вт/(м-град), стали λ2=34,9 Вт/(м-град) и алюминия λ3 = 422 Вт/(м-град) термическое сопротивление контакта между слоями окиси циркония и стали Rkl = 0,258 ∙ 10-3 (м2∙ град)/Вт, а между слоями стали и алюминия Rk2 = 0,266 ∙ 10-3 (м2∙ град)/Вт. № 12. Для условия задачи №11 определить температуры на контактирующих поверхностях каждого слоя. № 13. Стенка камеры сгорания РД диаметром 200/206 мм покрыта с внутренней стороны слоем тугоплавкого покрытия толщиной б= 1 мм; коэффициенты теплопроводности стенки камеры и покрытия соответственно равны λW = 41,8 Вт/(м-град) и λ п = 1,395 Вт/(м-град), температура на внутренней поверхности покрытия tWl = 2500° С и на внешней поверхности стенки tW3 = 500° С. Определить удельный тепловой поток на единицу длины стенки и температуры поверхностей стенок в зоне контакта, если термическое сопротивление контакта Rk=0,757∙10-3 (м2 ∙град)Вт. № 14. Стальные шины прямоугольного сечения 90x3 мм находятся под током 320 А. Максимальная температура шины при температуре воздуха 20° С не должна превышать 75° С. Определить объемную производительность внутренних источников теплоты и температуру на поверхности шины, если коэффициент теплопроводности шины 57Вт/ (м-град), а удельное электрическое сопротивление ее р = 0,13 Ом ∙ мм2/м. Определить также, каким должен быть коэффициент теплоотдачи с поверхности шины, чтобы температура ее не превышала 75° С.  Задача № 15. Решить задачу №14 при условии, что шины изготовлены из латуни, удельное электрическое сопротивление которых ρ = 0,04 Ом•мм2/м и коэффициент теплопроводности λ = 104,7 вт/(м-град). Задача № 16. По стержню из нержавеющей стали диаметром d=10 мм проходит электрический ток силой I = 200 а. Вся теплота, выделяемая в стержне, отводится через его наружную поверхность. Определить объемную производительность источников теплоты и максимальную температуру стержня, если температура на поверхности стержня tW= 50° С, удельное электрическое сопротивление р=0,85 ом-мм2/м и коэффициент теплопроводности стержня λ =18,6 вт/(м-град) Контрольные вопросы Что описывают уравнения (2.3) и (2.4), приведенные в [4, с.25]? Что рассчитывается по уравнениям (2.7) и (2.9.)? Запишите указанные уравнения, дайте все пояснения, приведите рисунок. Что рассчитывается по уравнению (2.22), приведенному в [4, с.30]? Как называются слагаемые знаменателя этого уравнения и как они связаны с перепадами температур (tж1 – tс1), (tс1– tс2), (tс2 – tж2)? Дайте понятие коэффициента теплопередачи плоской стенки. Запишите все уравнения с пояснениями, приведите рисунок. Запишите уравнение, по которому можно рассчитать плотность теплового потока q, Вт/м2, передаваемого от среды с температурой tж1 в среду с температурой tж2 через трехслойную плоскую стенку. Приведите график перепадов температур для условия: α1>>α2, λ1>> λ2, λ1 >>λ3, λ2 >λ3. Что описывают уравнения (2.35) и (2.36), приведенные в [4], с.33? Что рассчитывается по уравнениям (2.39) и (2.40)? Запишите указанные уравнения, дайте все пояснения, приведите рисунок. Что рассчитывается по уравнению (2.49), приведенному в [4], с.36? Запишите уравнение с пояснением, приведите рисунок. Можно ли расчет теплопередачи через цилиндрическую стенку производить по уравнению для плоской стенки? Запишите уравнение, по которому можно рассчитать линейную плотность теплового потока (q 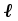 , Вт/м), передаваемого от горячей воды с температурой tж1 к окружающему воздуху с температурой tж2 через стенку трубы, покрытой одним слоем тепловой изоляции. Приведите график перепадов температур для условия: α1>>α2, λтр>>λиз. , Вт/м), передаваемого от горячей воды с температурой tж1 к окружающему воздуху с температурой tж2 через стенку трубы, покрытой одним слоем тепловой изоляции. Приведите график перепадов температур для условия: α1>>α2, λтр>>λиз.Дайте понятие критического диаметра изоляции. Как изменятся теплопотери (Q, Вт), если наложить изоляцию на трубу, наружный диаметр которой: а) d2 Что описывают уравнения (2.61) и (2.62), приведенные в [4], с.40? Что рассчитывается по уравнениям (2.64) и (2.65)? Запишите указанные уравнения, дайте все пояснения, приведите рисунок. Что рассчитывается по уравнению (2.66), приведенному в [4], с.41? Запишите уравнение с пояснением, приведите рисунок. Что рассчитывается по уравнениям (2.90) и (2.87), приведенным в [4], с.49-50? Поясните все величины, входящие в уравнения, приведите рисунок. Что рассчитывается по уравнению (2.85), приведенному в [4], с.41? Запишите это уравнение и поясните все величины его правой части. Дайте рисунок с расстановкой размеров. Какими способами можно увеличить тепловой поток Q, Вт, передаваемый через стенку от среды с температурой tж1 к среде с температурой tж2 при условии, что α1>>α2? Каков механизм передачи тепла теплопроводностью в газах? От каких факторов зависит коэффициент теплопроводности газов? Сравните коэффициенты теплопроводности легких и тяжелых газов. Каков механизм передачи тепла теплопроводностью в металлах? Как зависит коэффициент теплопроводности от температуры для чистых металлов, для сплавов? От каких факторов зависит коэффициент теплопроводности строительных и теплоизоляционных материалов? В каких пределах он изменяется? Приведите значения коэффициентов теплопроводности для кирпича, стекловаты, асбеста [4], табл.3, с. 401. Каков механизм передачи тепла теплопроводностью в жидкостях? От каких факторов зависит коэффициент теплопроводности жидкостей? Приведите пределы изменения l для жидкостей. Дайте понятие коэффициента температуропроводности. Как он обозначается, какую имеет размерность, что характеризует, от каких факторов зависит? Рассчитайте коэффициент температуропроводности для шлакобетона и льда при t=00С. Воспользуйтесь [4], табл. 3, с. 401-402. Дайте понятие температурного поля. Приведите практические примеры температурных полей: 1) стационарного одномерного; 2) нестационарного одномерного; 3) стационарного трехмерного; 4) нестационарного двухмерного. Дайте полную характеристику дифференциального уравнения 1.27 [4, с.19], поясните все величины, входящие в уравнение; укажите, какие процессы передачи тепла и в каких телах описывает данное уравнение. Какие процессы передачи тепла и в каких телах описывает уравнение 1.27 [4, с.19]? Запишите это уравнение для стационарной теплопроводности в телах: а) с внутренними источниками тепла; б) без внутренних источников тепла. Приведите примеры таких процессов. Что включают в себя условия однозначности? Для чего они нужны? Как формулируются граничные условия первого, второго и третьего рода? Для чего они присоединяются к дифференциальному уравнению? Приведите математическое выражение закона Фурье: а) для теплового потока Q, Вт; б) для плотности теплового потока q, Вт/м2. Какой способ передачи тепла описывает закон Фурье? Чем объяснить знак (-) в правой части уравнения Фурье? Дайте понятие изотермической поверхности. Могут ли две изотермические поверхности пересекаться? Какое направление называется нормалью к изотермической поверхности? Сравните между собой градиенты температуры по нормали и по любому другому направлению к изотермической поверхности. 2. Задание по расчету теплопередачи через многослойную стенку 2,1 Требуется рассчитать температурное поле в трехслойной цилиндрической или сферической стенке и определить тепловой поток через нее (стационарная задача, граничные условия 3-го рода). В задаче предполагается идеальный тепловой контакт между слоями стенки, т.е. термическое сопротивление контакта равно нулю и температуры контактирующих поверхностей равны между собой. Исходные данные для выполнения задания выдаются индивидуально каждому студенту и содержат числовые значения следующих величин (см.табл.П3.I и рис.П3.I): В записку отдельным пунктом включить: Уравнение температурного поля для каждого слоя (в общем виде и численном). График температурного поля по толщине составной стенки (на миллиметровой бумаге) в масштабе: а) толщина 1: 1; б) температура 1 мм — 2°С. Условные обозначения: tf1, tf2,°С- температуры горячей и холодной среды; α1,α2, Вт/(м2*К) - коэффициенты теплоотдачи на горячей и холодной стороне; λ1, λ2, λ2,Вт/(м*К) - коэффициенты теплопроводности материала слоев; tw1, tw2, tw3, tw4, °С- температуры поверхностей слоев. Для криволинейных стенок tw1, λ1, R1 относятся к внутренней поверхности. По толщине каждого слоя рассчитать две промежуточные точки. Указание к заданию 1 При решении задачи сначала рассчитывается коэффициент теплопередачи многослойной стенки, затем величина теплового потока. По найденной величине теплового потока определите распределение температурного поля в каждом слое. Расчет цилиндрической стенки Линейный коэффициент теплопередачи ( в  ) ) Где n – число слоев (n=3); i – номер слоя. Линейная плотность теплового потока ( в  ) ) . .Температуры поверхностей слоев (  ) ) , ,Таблица 1 Исходные данные к заданию № 1 по расчету цилиндрической и сферической стенки
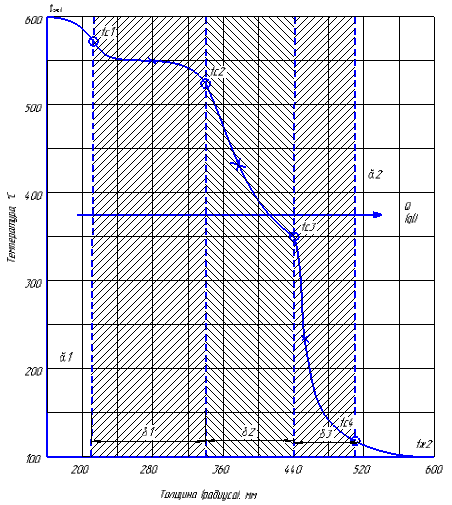 по этой формуле определяется:  ; ;в частности, для определения  следует принять i=0. следует принять i=0.Правильность расчетов  проверяется расчетом проверяется расчетом  , как по вышеприведенной формуле, так и по закону теплопередачи с внешней стороны стенки ( , как по вышеприведенной формуле, так и по закону теплопередачи с внешней стороны стенки ( ): ): (результаты расчетов  не должны отличаться более, чем на 3%). не должны отличаться более, чем на 3%).Выводятся уравнения температурного поля каждого слоя (  ): ): Например, для слоя №1:  Уравнение температурного поля каждого слоя приводится к виду  , где , где 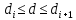  и и 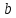 - численные коэффициенты, постоянные для каждого слоя. - численные коэффициенты, постоянные для каждого слоя. По уравнению температурного поля рассчитываются 2…3 промежуточных значения температур в каждом слое, задаваясь соответственно промежуточными значениями  для каждого слоя. для каждого слоя.Строится график температурного поля по толщине 3-слойной стенки (рис.П3.I), на который наносятся рассчитанные значения температур поверхностей слоев и промежуточные значения температур в каждом слое (на миллиметровой бумаге). Масштабы данной схемы: толщина – 1:1, температура – 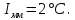 На координатных осях наносятся равномерные значения t и R. На координатных осях наносятся равномерные значения t и R.2,2 Порядок расчета сферической стенки Тепловой поток ( в ВТ) через стенку  Где n – число слоев (n=3); I – номер слоя. Температуры (  ) поверхностей слоев ) поверхностей слоев по этой формуле определяются  проверка:  результаты расчета  не должны отличаться более, чем на 3%. не должны отличаться более, чем на 3%.Выводятся уравнения температурного поля (  ) каждого слоя. ) каждого слоя. где 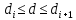 . .Уравнение температурного поля каждого слоя приводится к виду где a и b – численные коэффициенты, постоянные для каждого слоя. По уравнению температурного поля расчитываются 2…3 промежуточных значения температур в каждом слое, задаваясь соответственно промежуточными значениями d для каждого слоя. Строится график температурного поля по толщине 3-слойной стенки (рис.3П.1), на который наносятся рассчитанные значения температур поверхностей слоев и промежуточные значения температур в каждом слое (на миллиметровой бумаге) Масштабы: толщина – 1:1, температура – 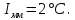 На координатных осях наносятся равномерные значения t и R. На координатных осях наносятся равномерные значения t и R.В случае  (тепловой поток направлен внутрь) можно использовать те же расчетные формулы, подставляя в них отрицательное значение Q. Это указание справедливо и для цилиндрической стенки. (тепловой поток направлен внутрь) можно использовать те же расчетные формулы, подставляя в них отрицательное значение Q. Это указание справедливо и для цилиндрической стенки.График температурного поля в этом случае будет иметь вид, изображенные на рис.П3.1 пунктиром. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 ,
,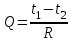


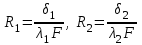

 , граничные условия первого рода
, граничные условия первого рода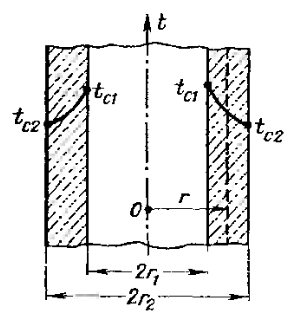

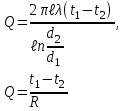




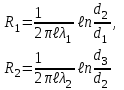




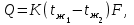
 - коэффициент теплопередачи
- коэффициент теплопередачи - полное термическое сопротивление
- полное термическое сопротивление