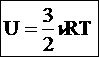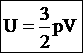Неорганическая химия, ответы. 1. Строение атома. Атом

• Название: 1. Строение атома. Атом
• Дата: 14.03.2018
• Размер: 436.56 Kb.
• Имя файла: Неорганическая химия, ответы.docx
• Тип: Документы; #38501
• страница: 6 из 11

(44) 45. Внутренняя энергия системы. Внутренней энергией U называется энергия системы, зависящая только от ее термодинамического состоянии. Для системы, нe подверженной действию внешних сил и находящейся в состоянии макроскопического покоя, внутренняя энергия представляет собой полную энергию системы. В некоторых простейших случаях внутренняя энергия равна разности между полной энергией W системы и суммой кинетической энергии WK ее макроскопического движения и потенциальной энергии Wп, обусловленной действием на систему внешних силовых полей:
U = W - (Wk + Wп)

Сумма кинетических  энергий хаотического движения всех частиц тела относительно центра масс тела  (молекул, атомов) и потенциальных энергий  их  взаимодействия друг с другом называется внутренней энергией.
Внимание! Энергия упорядоченного движения частиц тела представляет собой механическую кинетическую энергию тела. Вообще говоря, во внутреннюю энергию входят энергии внутриатомных частиц, но при не очень больших температурах эта энергия остается неизменной. Кинетическая энергия частиц определяется скоростью, а значит - температурой тела. Потенциальная - расстоянием между частицами, а значит - объемом. Следовательно: U=U(T,V) - внутренняя энергия зависит от объема и температуры.	U=U(T,V)
Для идеального газа: U=U(T), т.к. взаимодействием на расстоянии пренебрегаем.  - внутренняя энергия идеального одноатомного газа. Внутренняя энергия - однозначная функция состояния (с точностью до произвольной постоянной) и в замкнутой системе сохраняется. Обратное неверно(!) - одной и той же энергии могут соответствовать разные состояния.	Идеальный  газ:
Опыты Джоуля доказали эквивалентность работы и количества теплоты, т.е. и та и другая величины являются мерой изменения энергии, их можно измерять в одинаковых единицах: 1 кал = 4,1868 Дж ≈ 4,2 Дж. Эта величина наз. механическим эквивалентом теплоты.
Р.Майер, Д.Джоуль, Г.Гельмгольц - закон сохранения энергии для тепловых процессов - 1-й закон термодинамики.
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
Изменений внутренней энергии не зависит от способа, которым осуществляется этот переход. Т.о. существует два способа изменения внутренней энергии: совершение механической работы и теплопередача (теплообмен). Работа и количество теплоты характеризуют процесс изменения внутренней энергии, но не саму внутреннюю энергию.
Если А - работа внешних сил, а А' - работа газа, то А = -  А'(в соответствии с 3-м законом Ньютона). Тогда: - другая форма записи первого закона термодинамики.Количество теплоты, переданное системе,  идет на изменение ее  внутренней энергии и на совершение системой работы над внешними телами.
Невозможность создания вечного двигателя 1-го рода. Вечный двигатель первого рода - устройство, которое могло бы совершать неограниченное количество работы без затраты энергии. Тогда Q=0. Следовательно: A'= - ΔU. Т.е. такой двигатель должен совершать работу за счет убыли внутренней энергии. Но ее запасы конечны. После того, как запас энергии будет исчерпан, двигатель остановится.

46. Растворы неэлектролитов. Первый и второй законы Рауля. РАСТВОРЫ НЕЭЛЕКТРОЛИТОВ, бинарные или многокомпонентные мол. системы, состав к-рых может изменяться непрерывным образом (по крайней мере, в нек-рых пределах). В отличие от растворов электролитов, в растворах неэлектролитов (мол. р-рах) заряженные частицы в сколько-нибудь заметных концентрациях отсутствуют. Растворы неэлектролитов могут быть твердыми, жидкими и газообразными. Значительное влияние на физические свойства растворов (в частности, на рассеяние света) оказывают флуктуации плотности, концентрации, ориентации молекул. Роль флуктуации концентрации особенно велика вблизи критической точки растворимости.
Поскольку образование р-ра при смешении жидкостей - самопроизвольный процесс, то G_m < 0.

Первый закон Рауля связывает давление насыщенного пара над раствором с его составом; он формулируется следующим образом:

Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причём коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

{\displaystyle P_{i}=P_{i}^{o}X_{i}}

Для бинарного раствора, состоящего из компонентов А и В (компонент А считаем растворителем), удобнее использовать другую формулировку:

Относительное понижение парциального давления пара растворителя над раствором не зависит от природы растворённого вещества и равно его мольной доле в растворе.

{\displaystyle {{{\rm {(}}P_{A}^{o}-P_{A}{\rm {)}}} \over {P_{A}^{o}}}=X_{B}}
Растворы, для которых выполняется закон Рауля, называются идеальными. Идеальными при любых концентрациях являются растворы, компоненты которых очень близки по физическим и химическим свойствам (оптические изомеры, гомологи и т. п.), и образование которых не сопровождается изменением объёма и выделением либо поглощением теплоты. В этом случае силы межмолекулярного взаимодействия между однородными и разнородными частицами примерно одинаковы, и образование раствора обусловлено лишь энтропийным фактором.

Тот факт, что давление паров над раствором отличается от давления паров над чистым растворителем, существенно влияет на процессы кристаллизации и кипения. Из первого закона Рауля выводятся два следствия, касающиеся понижения температуры замерзания и повышения температуры кипения растворов, которые в объединённом виде известны как второй закон Рауля.

Понижение температуры кристаллизации растворов

Условием кристаллизации является равенство давления насыщенного пара растворителя над раствором давлению пара над твёрдым растворителем. Поскольку давление пара растворителя над раствором всегда ниже, чем над чистым растворителем, это равенство всегда будет достигаться при температуре более низкой, чем температура замерзания растворителя. Так, океанская вода начинает замерзать при температуре около −2 °C.

Разность между температурой кристаллизации растворителя T°_fr и температурой начала кристаллизации раствора T_fr есть понижение температуры кристаллизации.

Понижение температуры кристаллизации бесконечно разбавленных растворов не зависит от природы растворённого вещества и прямо пропорционально моляльной концентрации раствора.

{\displaystyle T_{fr}^{o}-T_{fr}=\Delta T_{fr}=Km}Поскольку по мере кристаллизации растворителя из раствора концентрация последнего возрастает, растворы не имеют определённой температуры замерзания и кристаллизуются в некотором интервале температур.

Повышение температуры кипения растворов

Жидкость кипит при той температуре, при которой общее давление насыщенного пара становится равным внешнему давлению. Если растворённое вещество нелетуче (то есть давлением его насыщенных паров над раствором можно пренебречь), то общее давление насыщенного пара над раствором равно парциальному давлению паров растворителя. В этом случае давление насыщенных паров над раствором при любой температуре будет меньше, чем над чистым растворителем, и равенство его внешнему давлению будет достигаться при более высокой температуре. Таким образом, температура кипения раствора нелетучего вещества T_b всегда выше, чем температура кипения чистого растворителя при том же давлении T°_b.

Повышение температуры кипения бесконечно разбавленных растворов нелетучих веществ не зависит от природы растворённого вещества и прямо пропорционально моляльной концентрации раствора

47. Принцип Паули. В атоме не может быть даже двух электронов, имеющих одинаковый набор всех четырех квантовых чисел. Следствие: каждая АО может быть занята не более чем двумя электронами, причем их спиновые квантовые числа должны быть различными.

48. Напишите продукты ОВРи подберите коэффициенты. Приведите уравнение Нернста для полуреакций. 2 KMnO₄ + 10 FeSO₄ + 8 H₂SO₄ = K₂SO₄ + 2 MNSO₄ + 5 Fe₂(SO₄)₃ + 8 H2O Метод электронно-ионного баланса (метод полуреакций) :
Составляют электронно-ионные уравнения полуреакций окисления и восстановления:
Fe(2+) -e(-) = Fe(3+)
[MnO4](-) +H(+) + e(-) = Mn(2+) + H2O
Далее расставляют коэффициенты в полуреакциях, по-прежнему исходя из принципа сохранения заряда (т. е. общий заряд системы в правой части должен равняться заряду системы в левой части, имеется в виду обычная алгебраическая сумма зарядов) :
Fe(2+) -e(-) = Fe(3+) [Заряд в левой части: +2-(-1)=+3; в правой: +3]
[MnO4](-) +8H(+) + 5e(-) = Mn(2+) + 4H2O [Заряд в левой части: -1+8*(+1)+5*(-1) = -1 +8 -5 = +2; в правой части: +2 +0= +2]
Поскольку количество принятых окислителем электронов равно количеству отданных восстановителем электронов, обе части первой полуреакции необходимо домножить на 5. Получим соответственно:
5Fe(2+) - 5e(-) = 5Fe(3+)
[MnO4](-) +8H(+) + 5e(-) = Mn(2+) + 4H2O
Далее обе полуреакции можно просто сложить (алгебраически, как два уравнения в математике, и точно также привести "подобные"):
5Fe(2+) - 5e(-) + [MnO4](-) +8H(+) + 5e(-) = 5Fe(3+) + Mn(2+) + 4H2O
Приводим подобные:
5Fe(2+) + [MnO4](-) +8H(+) = 5Fe(3+) + Mn(2+) + 4H2O
Далее необходимо лишь учесть индексы в исходном молекулярном уравнении:
10FeSO4 + 2KMnO4 + 8H2SO4 -> 2MnSO4 + 5Fe2(SO4)3 + K2SO4 + 8H2O

Нернст изучал поведение электролитов при пропускании электрического тока и открыл закон. Закон устанавливает зависимость между электродвижущей силой (разностью потенциалов) и ионной концентрацией. Уравнение Нернста позволяет предсказать максимальный рабочий потенциал, который может быть получен в результате электрохимического взаимодействия, когда известны давление и температура. Таким образом, этот закон связывает термодинамику с электрохимической теорией в области решения проблем, касающихся сильно разбавленных растворов.

{\displaystyle E=E^{0}+{\frac {RT}{nF}}\ln {\frac {a_{\rm {Ox}}}{a_{\rm {Red}}}}}

{\displaystyle E=E^{0}+{\frac {0,0592}{n}}\lg {\frac {a_{\rm {Ox}}}{a_{\rm {Red}}}}} где E0 - стандартный потенциал редокс-системы; 
R - универсальная газовая постоянная, равная 8,312 Дж/(моль К);
T - абсолютная температура, К;
F - постоянная Фарадея, равная 96485 Кл/моль;
n - число электронов, принимающих участие в электродной реакции;
aox, ared - активности соответственно окисленной и восстановленной форм редокс-системы;
[ox], [red] - их молярные концентрации;
Гox, Гred - коэффициенты активности. E=E₀ при a_ox = a_red = 1, причем имеется в виду гипотетический стандартный 1 М раствор, в котором коэффициент активности каждого растворенного вещества равен 1, а чистые вещества находятся в наиболее устойчивом физическом состоянии при данной температуре и нормальном атмосферном давлении.

Подставляя T=298,15 и числовые значения констант в уравнение, получаем для 25 °C


Связь уравнения Нернста с константой равновесия[править|править вики-текст]

Рассмотрим следующие реакции:

{\displaystyle {a_{\rm {Ox}}}_{1}+ne\rightleftharpoons {a_{\rm {Red}}}_{1}}

{\displaystyle {b_{\rm {Red}}}_{2}-ne\rightleftharpoons {b_{\rm {Ox}}}_{2}}Для реакции а:

{\displaystyle E'=E_{{ox_{1}}/{red}_{1}}^{0}+{\frac {0,0592}{n}}\lg {\frac {[\mathrm {Ox} _{1}]^{a}}{[\mathrm {Red} _{1}]^{a}}}}

Для реакции b:

{\displaystyle E''=E_{{ox_{2}}/{red}_{2}}^{0}+{\frac {0,0592}{n}}\lg {\frac {[\mathrm {Ox} _{2}]^{b}}{[\mathrm {Red} _{2}]^{b}}}}

При установившемся равновесии окислительные потенциалы обеих систем равны E' = E, или:


{\displaystyle E_{{ox_{1}}/{red}_{1}}^{0}+{\frac {0,0592}{n}}\lg {\frac {[\mathrm {Ox} _{1}]^{a}}{[\mathrm {Red} _{1}]^{a}}}=E_{{ox_{2}}/{red}_{2}}^{0}+{\frac {0,0592}{n}}\lg {\frac {[\mathrm {Ox} _{2}]^{b}}{[\mathrm {Red} _{2}]^{b}}}}откуда:

{\displaystyle E_{{ox_{1}}/{red}_{1}}^{0}-E_{{ox_{2}}/{red}_{2}}^{0}={\frac {0,0592}{n}}[\lg {\frac {[\mathrm {Ox} _{2}]^{b}}{[\mathrm {Red} _{2}]^{b}}}-\lg {\frac {[\mathrm {Ox} _{1}]^{a}}{[\mathrm {Red} _{1}]^{a}}}]={\frac {0,0592}{n}}\lg {\frac {[\mathrm {Ox} _{1}]^{a}}{[\mathrm {Red} _{1}]^{a}}}{\frac {[\mathrm {Ox} _{2}]^{b}}{[\mathrm {Red} _{2}]^{b}}}}На основании уравнения: {\displaystyle K_{{ox}/{red}}={\frac {[\mathrm {Ox} _{1}]^{a}}{[\mathrm {Red} _{1}]^{a}}}{\frac {[\mathrm {Ox} _{2}]^{b}}{[\mathrm {Red} _{2}]^{b}}}}

{\displaystyle E_{{ox_{1}}/{red}_{1}}^{0}-E_{{ox_{2}}/{red}_{2}}^{0}={\frac {0,0592}{n}}\lg K_{{ox}/{red}}}или:

{\displaystyle {\frac {n(E_{1}^{0}-E_{2}^{0})}{0,0592}}=\lg K_{{ox}/{red}}}следовательно K_ox/red равна:

{\displaystyle K_{{ox}/{red}}=10^{\frac {(E_{1}^{0}-E_{2}^{0})n}{0,0592}}}
Рассмотрим вычисление K_ox/red на примере полуреакции:

{\displaystyle MnO_{4}^{-}+8H^{+}+5Fe^{2+}\rightleftharpoons Mn^{2+}+5Fe^{3+}+4H_{2}O}В ходе реакции протекают два ОВ-процесса — восстановление перманганат иона и окисление иона Fe³⁺ по уравнениям:

{\displaystyle MnO_{4}^{-}+8H^{+}+5e\rightleftharpoons Mn^{2+}+4H_{2}O}

{\displaystyle Fe^{2+}-e\rightleftharpoons Fe^{3+}}Количество электронов, принимающих участие в полуреакции 5, то есть n = 5; стандартные потенциалы для участников полуреакции:

{\displaystyle E_{{MnO_{4}^{-}}/{Mn^{2+}}}^{0}=1,51V}

{\displaystyle E_{{Fe^{3}+}/{Fe^{2+}}}^{0}=0,77V}Находим К по уравнению:

{\displaystyle \lg K_{{MnO_{4}^{-}}/{Fe^{2+}}}={\frac {5(1,52-0,77)}{0,0592}}=63,5}.

Следовательно

{\displaystyle K_{{MnO_{4}^{-}}/{Fe^{2+}}}=10^{63,5}}

49. Нитропентацианоферра́т(III) ка́лия K₃[Fe(CN)₅ NO₂]

50.Приведите формулировку закона кратных отношений. Для каких веществ он несправедлив? (1803, Дж. Дальтон)

Если 2 элемента образуют друг с другом несколько химических соединений, то весовые количества одного элемента, соединяющиеся с одним и тем же весовым количеством другого элемента, относятся между собой как небольшие целые числа. Несправедлив для веществ в твердом состоянии.