Ответы на билеты по геодезии (2 курс). 1. Техническая последовательность работ при тахеометрической съемке
 Скачать 2.04 Mb. Скачать 2.04 Mb.
|
|
1. Техническая последовательность работ при тахеометрической съемке. Полевые работы при тахеометрической съемке на станции включают следующие действия: - установку прибора над точкой с известными координатами и приведение его в рабочее положение (допускается выполнять центрирование с погрешностью до 3 см, т.е. на порядок грубее, чем при измерении горизонтальных углов); - определение место нуля вертикального круга (п.28); - составление абриса на станции с указанием на нем положения реечных точек; - измерение высоты прибора с погрешностью 1-2 см; - ориентирование нуля лимба горизонтального круга на соседнюю точку съемочного обоснования, координаты которой известны; - наблюдение реечных точек при КЛ: определение расстояния от прибора до рейки по дальномеру, снятие отсчетов по горизонтальному и вертикальному кругам при наведении средней горизонтальной нити на определенный отсчет, например Vj = I; - вычисление углов наклона, неполных превышений и высот реечных точек по формулам n = Л - М0, h'= 0.5 D' sin2n, Hj= Hст+ h' + I - Vj. Если рельеф местности позволяет брать отсчет по рейке горизонтальным лучом визирования (в этом случае отсчет по ВК должен быть равен М0), то высоты реечных точек Нi= ГП - аi, где ГП - горизонт прибора ГП = Нст+ I; аi - отсчет по рейке горизонтальным лучом визирования. Результаты измерений и вычислений записывают в журнал тахеометрической съемки (табл.41). При камеральной обработке проверяют журналы тахеометрической съемки и исправляют ошибки вычислений. Затем с помощью тахеографа наносят на план пикетные (реечные) точки по значениям полярных углов и расстояний. Около пикетных точек выписывают их номера и высоты. В соответствии с абрисами рисуют на плане контуры угодий, элементы ситуации и обозначают их условными знаками. Для отображения рельефа проводят горизонтали. 2.Способы определения высот пикетов при тахеометрической съемке. Сущность тахеометрической съемки заключается в том, что плановое положение характерных (реечных) точек местности определяется полярным способом от линии теодолитного хода, а их высотное положение определяется одним из двух методов: геометрическим или тригонометрическим нивелированием. Расстояние от прибора до реек зависит от масштаба составляемого топоплана и для масштаба 1:1000 - допускается до 150 м, а между соседними реечными точками менее 35 м. При тахеометрической съемке высоты реечных точек в зависимости от условий местности получают при горизонтальном визировании (геометрическое нивелирование способом "вперед") или наклоном (тригонометрическое нивелирование). Используемые при этом формулы могут быть получены из рис. 41.2. При геометрическом нивелировании способом "вперед" сначала определяют горизонт прибора ГП = Нст+I. Затем устанавливают на вертикальном круге теодолита отсчет равный МО. Высоты реечных точек вычисляют по формуле Нi= ГП - аi, где аi - отсчеты по рейке при горизонтальном визировании. При тригонометрическом нивелировании реечных точек при КЛ наводят среднюю нить сетки на отсчет Vj (для упрощения последующих вычислений по возможности отсчет Vj должен быть равен высоте прибора I), снимают отсчет Л по ВК и вычисляют угол наклона n = Л - МО. Наклонное расстояние D от прибора до реечной точки определяют по штриховому (нитяному) дальномеру. Так как вертикально (отвесно) установленная рейка не перпендикулярна визирному лучу на величину угла наклона n, то D = D' cosn, d = D' cos2n, где D' - расстояние, определяемое по штриховому дальномеру и отвесно установленной рейке. 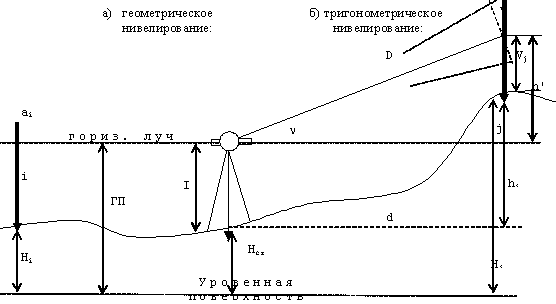 Тогда из прямоугольного треугольника (рис.41.2), у которого определены D и n, так называемое "неполное" превышение h'= D sinn = D' cosn sinn = (1/2)D' sin2n или h'= d tgn = D' cos2n sinn/cosn = (1/2)D'sin2n. На равнинной местности при углах наклона n < 5 "неполное" превышения можно вычислять по приближенной формуле: h'= D' sinn. Высоты реечных точек, определяемых тригонометрическим нивелированием, вычисляются по формуле: Hj= Hст+ h' + I - Vj. Если высота наведения Vj равна высоте прибора I, то формула вычисления высот упрощается Hj= Hст+ h'. 3.Последовательность работ при проложении тахеометрического хода. Тахеометрические ходы прокладывают при создании планового и высотного съемочного обоснования для производства тахеометрической съемки. Они могут также применяться при создании съемочного обоснования для топографических мензульных съемок и для привязки аэроснимков. Тахеометрические ходы могут прокладываться в виде одиночных замкнутых (полигонов) и разомкнутых ходов или в виде систем с координатами и отметками, полученными из более точных измерений. Длина сторон в тахеометрических ходах должна быть в пределах до 200 – 250 м. Так как расстояния в ходах измеряются. Как правило, дальномерами, то ходы можно прокладывать по пересеченной местности. Предельная длина тахеометрического хода зависит от масштаба съемки и от точности, с которой надо получить отметки точек или от принятой высоты сечения рельефа. Так, при масштабе 1:5000 и высоте сечения рельефа 1 м. Длину тахеометрического хода не следует принимать более 3 км. Проект ходов и положение пунктов уточняют при полевой рекогносцировке и закрепляют кольями длиной 30 – 40 см и толщиной 4 – 6 см с забитым в верхний торец каждого кола гвоздем. Углы наклона, измеренные при помощи теодолита 2Т – 30П вычисляют по формулам: n = КЛВ – М0. Измерение углов наклона контролируют постоянством места нуля М0, колебание которого допускается в пределах 1| ,5. Превышения между точками вычисляют в прямом и обратном направлениях, с допустимым расхождением между ними 4 см на каждые 100 м расстояния. 4.Методы определения положения ( в плане) пикетов при тахеометрической съемке. 1. Проверить полевые журналы и составить схему хода. 2. Вычислить координаты и высотные точки хода ВЫЧИСЛЕНИЕ ВЫСОТ ТОЧЕК ТАХЕОМЕТРИЧЕСКОГО ХОДА В ведомость вычисления высот точек тахеометрического хода выписать высоты 2-х исходных пунктов, затем из журнала тахеометрической съемки выписать средние значения горизонтальных проложениий, прямые и обратные превышения между точками тахеометрического хода. Если расхождения между прямыми и обратными значениями превышений допустимы (∆hдоп. ≤ 4см на 100м) вычислить их среднее значение с округлением до 0,01м по формуле: 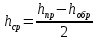 Допустимую невязку в сумме превышений вычислить по формуле: 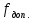 = =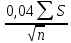 где ΣS – длина хода в метрах; n – число сторон в ходе. ВЫЧИСЛЕНИЕ КООРДИНАТ ТОЧЕК ТАХЕОМЕТРИЧЕСКОГО ХОДА Из журнала тахеометрической съемки выписать средние значения горизонтальных углов и средние значения горизонтальных проложений сторон тахеометрического хода, другие необходимые исходные данные (дир.углы, координаты). Вычислительная обработка тахеометрического хода выполняется аналогично вычислительной обработке теодолитного хода, а допустимую абсолютную невязку хода вычисляют по формуле: 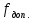 = =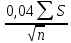 где ∑S – длина хода в метрах; n – число сторон в ходе 3.Вычислить высоты пикетных точек на каждой съемочной точке. 4. Внести пикетные точки на план. 5. Построить и оформить план. 5.Планово-высотное обоснование тахеометрической съемки. Методы создания. Допуски. Планово-высотное обоснование тахеометрических съемок, со съемочных точек которого осуществляют съемку подробностей рельефа и ситуации местности, обычно создают двумя способами: прокладкой теодолитного хода (разомкнутого или замкнутого) с измерением горизонтальных углов полным приемом оптического теодолита или электронного тахеометра и промерами горизонтальных проекций сторон землемерной лентой или светодальномером. Высоты съемочных точек определяют геометрическим нивелированием; прокладкой теодолитного хода с измерением горизонтальных углов полным приемом теодолита, определением горизонтальных расстояний между съемочными точками нитяным дальномером оптического теодолита или светодальномером электронного тахеометра (если тахеометрическую съемку выполняют электронным тахеометром). Высоты съемочных точек определяют методом тригонометрического нивелирования. Таким образом, в этом случае планово-высотное обоснование создают используя один прибор — оптический теодолит или электронный тахеометр.
Съемочное обоснование по первому способу создают при тахеометрических съемках для проектирования объектов, занимающих большие площади (средние и большие мостовые переходы, транспортные развязки движения в разных уровнях, аэропорты и т. д.), а также при съемках в населенных пунктах. Съемочное обоснование по второму способу создают при относительно небольших площадях тахеометрических съемок (места со сложными инженерно-геологическими условиями, небольшие карьеры и резервы, пересечения и примыкания автомобильных дорог в одном уровне, малые водопропускные сооружения и т. д.). Съемочным обоснованием тахеометрических съемок могут служить: трасса линейного сооружения, замкнутый полигон, сеть микротриангуляции и висячий ход. Выбор того или иного типа съемочного обоснования связан со стадией проектирования, рельефом местности, размерами и требуемым масштабом съемок. Ориентирование съемочного обоснования тахеометрических съемок и определение координат съемочных точек обычно осуществляют привязкой к трассе линейного сооружения либо к пунктам государственной геодезической сети. При съемках небольших площадей допускается ориентирование съемочного обоснования по магнитному азимуту с вычислением условных координат съемочных точек. На каждой точке съемочного обоснования производят работы в такой последовательности: на съемочной точке устанавливают теодолит или тахеометр, для чего его центрируют, устанавливают с помощью подъемных винтов по уровню в рабочее положение и с помощью рейки или рулетки измеряют высоту прибора над съемочной точкой обоснования; прибор ориентируют, т. е. устанавливают ноль лимба по исходному направлению (обычно на предыдущую съемочную точку обоснования), для чего открепив закрепительный винт алидады, совмещают ноль лимба с нулевым штрихом алидады, или иначе, устанавливают отсчет по горизонтальному кругу теодолита 0°00' и закрепляют алидаду; открепив закрепительный винт лимба, наводят перекрестье нитей зрительной трубы на низ вехи, установленной на предыдущей съемочной точке обоснования, закрепляют лимб и открепляют алидаду. Ориентирование осуществляют при основном положении круга теодолита; наведение прибора на реечные точки осуществляют при основном положении круга теодолита, при этом: измеряют расстояние нитяным дальномером, наводят горизонтальный штрих сетки нитей на определенный отсчет (на высоту наводки), измеряют угол наклона по вертикальному кругу, по лимбу горизонтального круга считывают горизонтальный угол, т. е. определяют направление на точку и записывают в графу «Примечания» семантическую информацию (угол дома, опора ЛЭП, урез воды и т.д.). При определении расстояния нитяным дальномером отсчеты по дальномерным нитям можно брать одним из следующих способов : с одновременным измерением угла наклона v, когда средний штрих сетки нитей наведен на отсчет, равный высоте прибора /, берут отсчеты по верхнему аи нижнему Ьштрихам нитяного дальномера (рис. 12, а); со смещением нижнего штриха дальномера на ближайший отсчет, кратный целому метру (рис. 16.2, б), при этом для взятия отсчета по вертикальному кругу теодолита средний штрих сетки нитей возвращают в исходное положение. 6.Тахеометрическая съемка. Назначение. Основные допуски. Тахеометрическая съемка представляет собой топографическую, т. е. Контурно-высотную съемку, в результате которой получают план местности с изображением ситуации и рельефа. Тахеометрическая съемка выполняется самостоятельно для создания планов небольших участков местности в крупных масштабах (1:500 – 1:5000) . Её применение особенно выгодно для съёмки узких полос местности при изысканиях трасс нефте и газопроводов, железных и автомобильных дорог, линий электропередач т. п. Быстрота измерений при тахеометрической съемке достигается тем, что положение снимаемой точки местности в плане и по высоте определяется при одном наведении трубы прибора на рейку, установленную на этой точке. Тахеометрическая съемка выполняется с помощью технических теодолитов или специальных приборов – тахеометров, в настоящее время как правило электронных. Допуски при выполнении тахеометрической съемки. 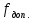 = 1` = 1`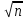 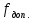 = = 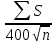 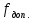 = =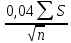 7.Последовательность математической обработки результатов измерений при тахеометрической съемке. Выполняют математическую обработку результатов полевых измерений, приведенных в журнале тахеометрической съемки. Для этого вычисляют место нуля и углы наклона между станциями по сторонам тахеометрического хода. Тахеометрическая съемка обычно выполняют при положении круга «лево». Величину места нуля (МО) определяют перед выполнением съемки и при необходимости приводят к нулю. Вычислить и занести в журнал для каждой станции среднее значение горизонтального угла, место нуля МО, углы наклона , горизонтальные проложения линий и превышения h между точками съемочного обоснования по формулам: где Л – отсчет по лимбу вертикального круга при положении "круг лево"; П – отсчет по лимбу вертикального круга при положении "круг право"; МО – отсчет по лимбу вертикального круга при горизонтальном положении визирной оси и горизонтального положения оси цилиндрического уровня при алидаде горизонтального круга; – угол наклона. Колебания значений МО на данной станции не должны превышать 1,5'. Превышения вычисляют по формуле: е D' = 100l+∆; l – дальномерный отсчет по рейке; - переменная величина, зависящая от расстояния между теодолитом и рейкой; - угол наклона; i - высота прибора над точкой; V - высота визирования на рейку Расхождения между результатами вычислений прямых и обратных превышений допускаются не более 4 см на 100 м. Расстояния между точками тахеометрического хода и пикетами определялись по нитяному дальномеру. Если углы наклона <|3°|, то принимается S =D′. Если >|3°|, то надо вычислять горизонтальные проложения по формуле: . 8.Сущность и виды измерений. Характеристики точности. Измерения – это процесс сравнения одной величины с другой ее однородной и принятой за единицу измерений. Геодезические измерения позволяют определить относительное расположение точек земной поверхности. Геодезические измерения бывают: 1. Линейные, в результате которых получают наклонные и горизонтальные расстояния между заданными точками. Для этой цели применяют мерные ленты, рулетки, проволоки, оптические и лазерные дальномеры. 2. Угловые, определяющие величины горизонтальных и вертикальных углов. Для выполнения таких измерений применяют угломерные инструменты: теодолиты, буссоли, эклиметры. 3. Высотные, в результате которых, получают разности высот отдельных точек. Для производства этих измерений применяют нивелиры, тахеометры и т.д. Полученные в процессе измерений данные заносят в специальные журналы. При этом процесс измерений в большинстве случаев сопровождается составлением на местности схематических чертежей, которые называются абрисами. Перечисленные выше виды измерений составляют содержание полевых геодезических работ. Измерения бывают непосредственные и косвенные. Непосредственными называют такие измерения, когда определяемую величину получают в результате непосредственного сравнения с единицей измерения (пример, определение длины стола обычной линейкой). Косвенными называют такие измерения, при которых определяемую величину получают, как функцию других непосредственно измеренных величин (например, длина окружности S=2πr, где измерен радиус данной окружности). Погрешности измерений Различают по характеру действий и причинам возникновения. По характеру действий: Грубые (из-за неисправности техники и промахов наблюдения). Исключают из дальнейшей обработки результатов измерений. Систематические (при многократных измерениях или изменяются по определенным законам, имеют одинаковый знак). Определяют и исключают из дальнейшей обработки Случайные порождаются не существенными, а второстепенными случайными связями между факторами измерений, при данных условиях измерений они могут быть, а могут и не появиться, могут быть большими или меньшими, положительными или отрицательными. Величина и знак этих погрешностей носит случайный характер, а их распределение подчинено законам теории вероятностей. Случайные погрешности ( не могут быть исключены из отдельного результата измерения. Влияние их на результаты измерений можно лишь ослабить, повышая квалификацию исполнителя, совершенствуя измерительные приборы и методику измерений, выполняя измерения при более благоприятных условиях. Влияние случайных погрешностей можно также ослабить надлежащей математической обработкой результатов измерений.)   Если грубые и систематические погрешности могут быть изучены и исключены из результата измерений, то случайные могут быть учтены на основе глубокого измерения. Изучение на основе теории вероятностей. На практике сложность заключается в том, что измерения проводятся какое-то ограниченное количество раз и поэтому для оценки точности измерений используют приближённую оценку среднего квадратического отклонения, которую называют среднеквадратической погрешностью (СКП). При оценке в качестве единицы меры точности используют среднеквадратическую погрешность с весом равным единице. Её называют средней квадратической погрешностью единицы веса СКП. Вес результата измерения определяют по формуле , (3.11) где – произвольно выбранное число одинаковое для всех весов, участвующих в решении задачи; – СКП результата измерения. Вес – относительная характеристика точности, т.е. он дает представление о точности результата измерения только при сравнении с весами других результатов измерений в данной задаче. 9.10.Классификация погрешностей измерений. Случайные погрешности измерений и их свойства. Нормальный закон распределения случайных погреностей. Истинное – такое значение измеряемой величины, которое идеальным образом отражало бы количественные свойства объекта. Истинное значение – это понятие гипотетическое, в реальности его достичь невозможно. Это величина, к которой можно приближаться бесконечно близко. Точность измерений– степень приближения его результата к истинному значению. Чем ниже погрешность, тем выше точность. Погрешности бывают следующих видов: Абсолютная погрешность выражается разностью значения, полученного в результате измерения и истинного измерения величины. Например, истинное значениеl= 100 м, однако, при измерении этой же линии получен результат 100,05 м, тогда абсолютная погрешность: E=Xизм–X E= 100,05 – 100 = 0,05 (м) Чтобы получить значение достаточно произвести одно измерение. Его называют необходимым, но чаще одним измерением не ограничиваются, а повторяют не менее двух раз. Измерения, которые делают сверх необходимого, называют избыточными (добавочными), они являются весьма важным средством контроля результата измерения. Абсолютная погрешность не даёт представления о точности полученного результата. Например, погрешность в 0,06 м может быть получена при измерении l= 100 м илиl= 1000 м. Поэтому вычисляют относительную погрешность: C=Eср/X C= 0,06 / 100 = 1/1667, т.е на 1667 м измеряемой величины допущена погрешность в 1 метр. Относительная погрешность– отношение абсолютной погрешности к истинному или измеренному значению. Выражают дробью. По инструкции линия местности должна быть измерена не грубее 1/1000. Погрешности, происходящие от отдельных факторов, называются элементарными. Погрешность обобщенная (Е) – это сумма элементарных. Возникают: грубые (Q), систематические (O), случайные (∆). Грубые погрешности измерений возникают в результате грубых промахов, просчётов исполнителя, его невнимательности, незамеченных неисправностях технических средств. Грубые погрешности совершенно недопустимы и должны быть полностью исключены из результатов измерений путем проведения повторных, дополнительных измерений. Систематические погрешности измерений – постоянная составляющая, связанная с дефектами: зрение, неисправность технических средств, температура. Систематические погрешности могут быть как одностороннего действия, так и переменного (периодические погрешности). Их стремятся по возможности учесть или исключить из результатов измерений при организации и проведении работ. Это составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины. Действительно, при выполнении со всей тщательностью повторных измерений обнаруживаются нерегулярные расхождения результатов измерений, обычно в последних двух-трех значащих цифрах. Такие расхождения в результатах измерений говорят о наличии в них случайных погрешностей. Случайные погрешности не могут быть исключены из результатов измерений как систематические погрешности. Случайные погрешности неустранимы и всегда присутствуют в результате измерения. Уменьшение случайных погрешностей возможно путем увеличения числа наблюдений. Описание случайных погрешностей возможно на основе теории случайных процессов (теории вероятностей) и математической статистики. Промах(грубая погрешность). Это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Результаты измерений, содержащие промах, не учитываются (отбрасываются). Причинами промахов обычно являются ошибки экспериментатора, резкое и неожиданное изменение условий измерения, неисправность измерительной аппаратуры и др. Для выявления промахов используют методы математической статистики. Теория случайных погрешностей, использующая математический аппарат теории вероятностей и математической статистики, основывается на рассмотрении случайных погрешностей при многократных измерениях как случайных величин. Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины(соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями). В практике измерений встречаются различные формы кривой закона распределения, однако чаще всего имеют дело с нормальным и равномерным законами распределения. При нормальном законе распределения малые случайные погрешности будут встречаться чаще, чем большие. При равномерном законе случайная погрешность может с одинаковой вероятностью принимать любое значение в заданных пределах E=Q+O+∆ Для изучения распределения случайных величин пользуются числовыми характеристиками: математическое ожидание и дисперсия. Если грубые и систематические погрешности могут быть изучены и исключены из результата измерений, то случайные могут быть учтены на основе глубокого измерения. Изучение на основе теории вероятностей. На практике сложность заключается в том, что измерения проводятся какое-то ограниченное количество раз и поэтому для оценки точности измерений используют приближённую оценку среднего квадратического отклонения, которую называют среднеквадратической погрешностью (СКП). Гауссом была предложена формула среднеквадратической погрешности: ∆2ср= (∆21+ ∆22+… +∆2n) /n, ∆2=m2= (∆21+ ∆22+… +∆2n) /n, ∆= m, ∆ср = m= √(∑∆2i/n) 11.Математическое ожидание, среднеквадратическая погрешность, предельная погрешность. Для изучения распределения случайных величин пользуются числовыми характеристиками: математическое ожиданиеидисперсия. Математическое ожидание также называют средним значением X(рисунок 1,а). Это число, характеризующее положение центра группирования.  Дисперсия случайной величины выражает мощность рассеяния отдельных ее значений относительно центра группирования. Чаще вместо дисперсии используют квадратный корень из дисперсии – среднее квадратическое отклонение 12.13.Математическая обработка результатов равноточных измерений одной и той же величины. При математической обработке ряда равноточных измерений одной и той же величины вычисляют: 1) среднеарифметическое значение измеренной величины (как наиболее надежное) X=  где Xi – результаты измерений некоторой величины; n – количество измерений; 2) СКП одного измерения по формуле Бесселя:  где V = X – Xi – уклонения от среднего арифметического значения X; 3)СКП среднеарифметического: 4) СКП самой СКП  Примеры : стр.25 методички за 1 семестр 14 Формулы Гаусса и Бесселя для равноточныхи неравноточных измерений Дл  я решения этой задачи К. Ф. Гауссом была предложена формула средней квадратичной погрешности: я решения этой задачи К. Ф. Гауссом была предложена формула средней квадратичной погрешности:С  редняя квадратичная погрешность обозначена через m и возведена в квадрат. Погрешности каждого измерения в этой формуле также возведены в квадрат, их сумма разделена на количество погрешностей n. Отсюда: редняя квадратичная погрешность обозначена через m и возведена в квадрат. Погрешности каждого измерения в этой формуле также возведены в квадрат, их сумма разделена на количество погрешностей n. Отсюда:Средняя квадратичная погрешность данного ряда измерений физической величины равна корню квадратному из дроби, в числителе которой сумма квадратов погрешностей измерений, а в знаменателе – количество измерений. Формула Гаусса применяется, когда вычисления выполняются по истинным погрешностям, т.е. когда известно истинное значение измеряемой величины. Вычисления средней квадратичной погрешности m выполняют так же по формуле Бесселя: В  формуле Бесселя в числителе под корнем квадратным представлена сумма квадратов уклонений результатов измерений от среднего арифметического значения измеряемой величины (арифметической середины, или вероятнейшего значения). формуле Бесселя в числителе под корнем квадратным представлена сумма квадратов уклонений результатов измерений от среднего арифметического значения измеряемой величины (арифметической середины, или вероятнейшего значения).15. Оценка точности функций от результатов измерений Оценка точности результатов измерений Под точностью измерений понимается степень близости результата измерения к истинному значению измеряемой величины. Точность результата измерений зависит от условий измерений. Для равноточных результатов измерений мерой точности является средняя квадратическая ошибка m, определяемая по формуле Гаусса:  . .Средняя квадратическая ошибка обладает устойчивостью при небольшом числе измерений. Предельная ошибка. Вследствие третьего свойства случайные ошибки, превышающие по абсолютной величине значение 2m, встречаются редко (5 на 100 измерений). Еще реже погрешности больше 3m (3 из 1000 измерений). Поэтому утроенную погрешность называют предельной ошибкой Для особо точных измерений в качестве предельной ошибки принимают Все вышеперечисленные ошибки называют абсолютными. В геодезии в качестве специальных характеристик точности измерений используется относительная ошибка – отношение абсолютной ошибки к среднему значению измеряемой величины, которое выражается в виде простой дроби с единицей в числителе, например  16. Неравноточные измерения. Вес измерения. Свойства весов. При математической обработке неравноточных измерений одной и той же величины решаются последовательно следующие задачи: 1) определяют средневесовое значение из результатов измерений  где Xi – результаты измерений некоторой величины; [ p] – сумма весов; 2) определяют СКП единицы веса по формуле: 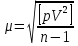 3) вычисляют СКП средневесового значения 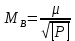 Для удобства вычислений применяется табличная форма. В зависимости от условия задачи для различных видов измерений веса можно вычислять по следующим формулам: 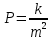 ; ; 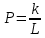 ; ;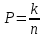 ; ; 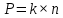 где k = 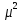 – произвольно выбранное число равное квадрату СКП единицы веса; – произвольно выбранное число равное квадрату СКП единицы веса;L – длина нивелирного хода в км, n – число углов поворота в теодолитном ходе или число станций в нивелирном ходе. Вес является относительной характеристикой точности результатов измерений. О весе логично говорить только тогда, когда сравнивают 2 и более результатов величин. Свойства весов: 1)Отношения весов не изменится, если их уменьшить или увеличить в одинаковое число раз. 2)Отношение весов обратнопропорционально отношению квадратов среднеквадратической погрешности. 17.Вычисление весов функции. Привести примеры.   18.Обратный вес функции. Найти обратный вес функции 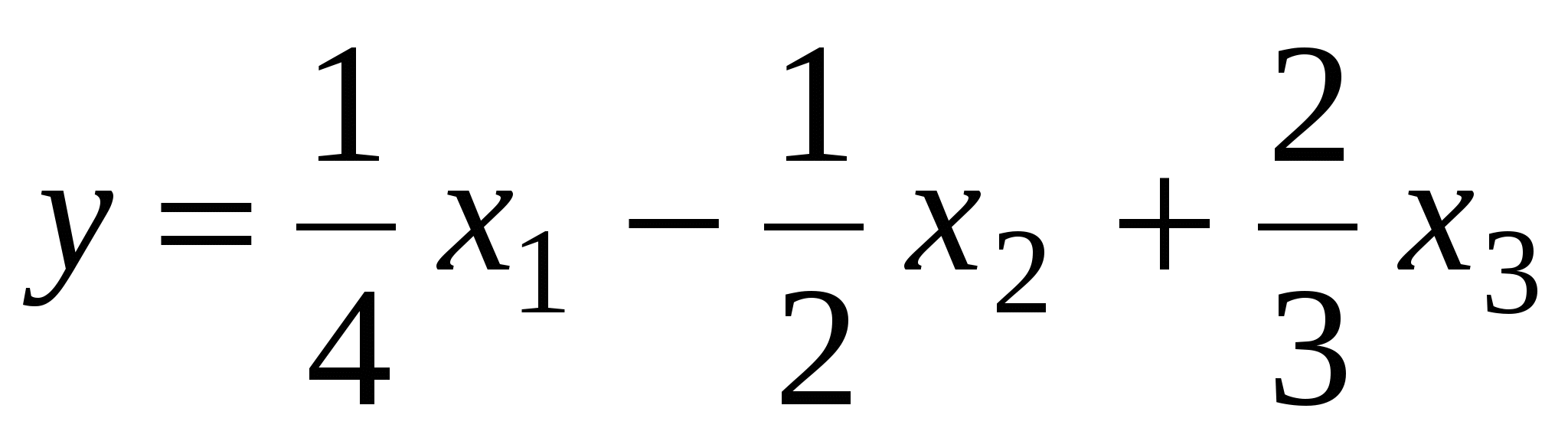 если веса аргументов соответственно равны р1=0,25,р2 = 0,50,р3=1,0. Решение. По формуле (1.29) находим 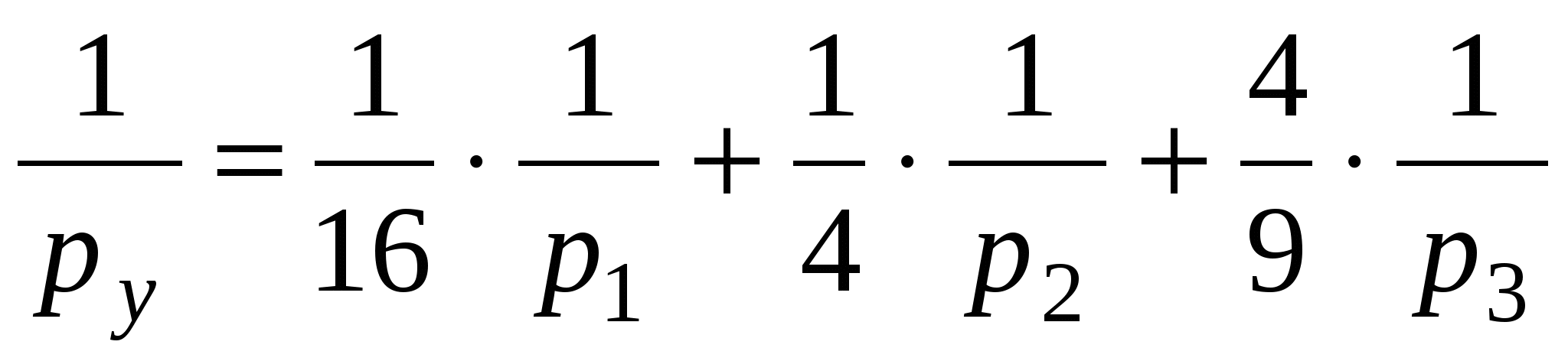 или или 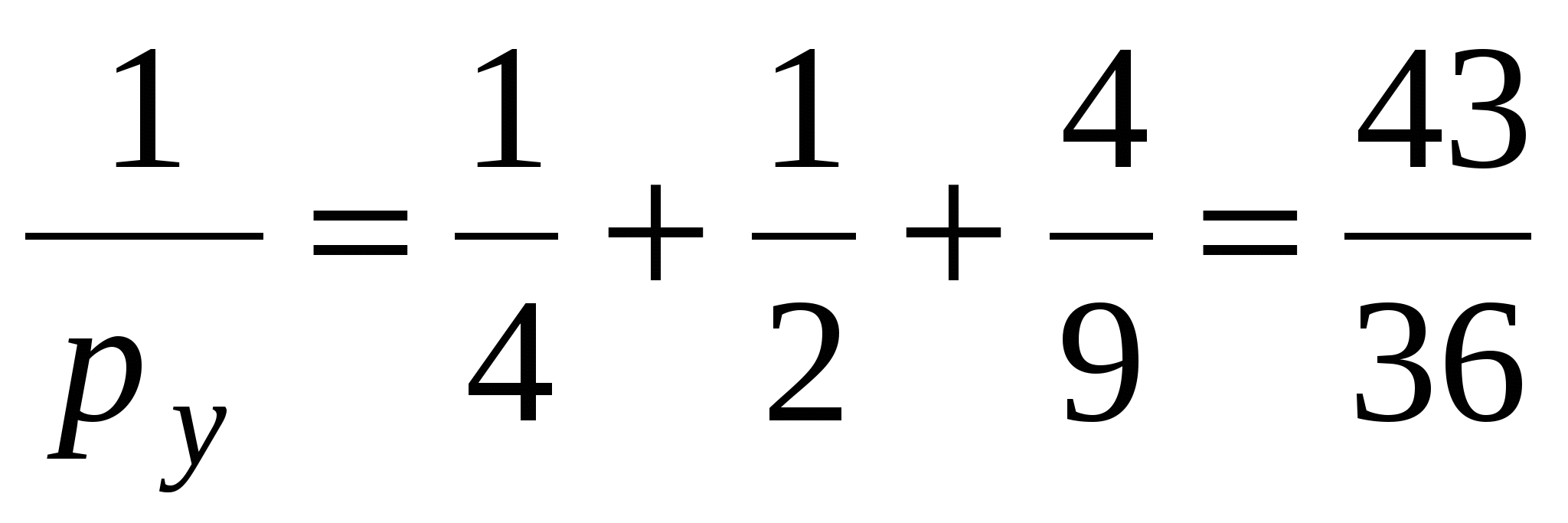 Отсюда py= 0,84. 19. Математическая обработка ряда неравноточных измерений. Приветси числовой пример    20. Оценка точности измерений по невязкам в полигонах и ходах.    21. Расчет технических допусков для расхождений и невязок в геодезиеских измерениях.   22. Свойства попровок равноточных измерений и неравноточных измерений(Вывод формул :[V]=0,[PV]=0). Если имеется ряд равноточных измерений одной и той же величины и из результатов измерений получено среднее арифметическое значение, то поправкой называют разность между средним арифметическим и результатом измерения, т. е. Укажем на два свойства поправок равноточных измерений одной и той же величины: (53) (54) Чтобы доказать первое свойство, просуммируем все равенства (52) с индексом i от 1 до n и получим (55) Подставим в это равенство вместо L его выражение . Тогда Это свойство поправок используют для контроля правильности вычисления и , (i= 1, 2, …, n). Если значение L получено с округлением величины частного , то где — погрешность округления. В этом случае равенство (53) точно выполняться не будет, а вместо него должно выполняться соотношение которое получается, если равенство (55) подставить выражение (56). Так как единицы последнего знака L, то должно выполняться условие единиц того же разряда. Все контроли остаются без изменения и при вычислении L через . Смысл второго свойства заключается в том, что сумма квадратов отклонений (поправок) результатов измерений от среднего арифметического всегда меньше, чем от любого другого числа. Чтобы убедиться в справедливости этого, возьмем функцию Для этого определим Приравняв эту производную к нулю и решив полученное равенство относительно х, найдем Следовательно. Легко проверить, что при этом значении х величина z будет иметь минимум, т. е. . 23. Средняя квадратичная погрешность единицы веса. На основании формулы (4.97) можно сделать вывод, что веса результатов измерений – положительные числа, обратно пропорциональные квадратам средних квадратических погрешностей этих результатов. Пусть в ряду результатов измерений xi существует такой xj, вес которого равен единице, т.е. pj = 1. Тогда Величину Из выражения (4.97) видно также, что или 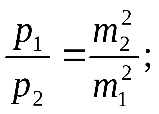 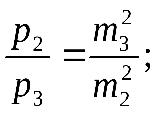  (4.109) (4.109)24. Последовательность уравнивания системы теодолитных ходов с одной узловой точкой. Привести необходимые формулы. Составляют схематический чертеж согласно заданному варианту. Уравнивание углов выполняется в следующем порядке. 4.3.1. Выбирают узловую линию, т.е. линию, примыкающую к узловой точке 5. При выборе в качестве узловой линии 4-5 (что рекомендуется сделать), решаемая система разделится на три одиночных теодолитных хода, которые опираются на исходные пункты. 4.3.2. Для каждого хода по координатам исходных пунктов решают обратные геодезические задачи и находят исходные дирекционные углы. Со схемы ходов выписывают в ведомость координат измеренные углы и исходные дирекционные углы по трем одиночным ходам. Подсчитывают суммы измеренных углов по каждому ходу. 4.3.3. Находят значения дирекционных углов узловой линии по каждому ходу по формулам: где –число углов, входящих в сумму Результаты вычислений выписывают в графу 2 табл. 4.1. Попутно в графу 3 записывают число углов n по каждому ходу. Таблица 4.1 |
