Ответы на билеты по геодезии (2 курс). 1. Техническая последовательность работ при тахеометрической съемке

• Название: 1. Техническая последовательность работ при тахеометрической съемке
• Дата: 03.06.2022
• Размер: 2.04 Mb.
• Имя файла: Ответы на билеты по геодезии (2 курс) .docx
• Тип: Документы; #567038
• страница: 3 из 5

25. Передача координат с вершины знака на землю. Чертеж. Оценка точности.

Эта задача возникает в том случае, когда требуется произвес­ти привязку полигонометрического (теодолитного) хода к пункту А с известными координатами вершины знака (рис.1), на который нельзя стать с прибором (например, пункт А - шпиль башни). Для выполнения привязки хода выбирают вблизи пункта А на земле пункт Р в таком месте, чтобы с него был виден пункт А и два удаленных исходных пункта В и С (один из них для контроля определения коор­динат пункта Р).

Сущность задачи заключается в передаче координат с пункта А на пункт Р.

Для решения задачи (с контролем ) измеряют два базиса в, в' и шесть углов: β₁, β₂, 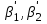, δ, δ’ (рис. 1), причём второй базис и углы при нём используют для контроля определения расстояния АР = d и повышения точности его окончательного значения, а угол δ’- для контроля правильности произведённых измерений и повышения точности определения координат пункта Р.




рис.1




Второе решение задачи, с участием базиса в' и координат пункта С (вместо В) производят по аналогичным формулам.




Вычисления выполняют по приведенным схемам.

1.Вычисление α, α', S, S'.

Значения α и α' вычисляют до секунд.

При вычислении S и S^’ могут получаться большие расхождения (до 0,10 м ). Убедившись в правильности вычислений, за окончатель­ное значение S или S' следует взять полученное по большему (по абсолют­ной величине) значению разности координат. Окончательный результат подчеркивают.







26. Прямая засечка. Формула Юнга. Чертеж. Оценка точности

Сущность задачи состоит в определении координат третьего пункта по координатам двух исходных и двум измеренным углам при этих пунктах. Для контроля определения измеряют еще угол при третьем исходном пункте.

В зависимости от того, какие углы измерены, задачу решают либо по формулам Юнга, либо по формулам Гаусса.

2.1. Решение задачи по формулам Юнга.

Формулы Юнга применяют в том случае, когда измерены внутренние углы треугольника (рис. 2), т.е. когда между исходными пунктами имеется видимость.

В этом случае вычисляют координаты пункта Р по координатам исходных пунктов А и В и измеренным при них углам β₁и β₂ (рис. 2 ). Для контроля и повышения точности результата решают задачу второй раз, используя в качестве исходных пункты В и С и измеренные углы _.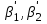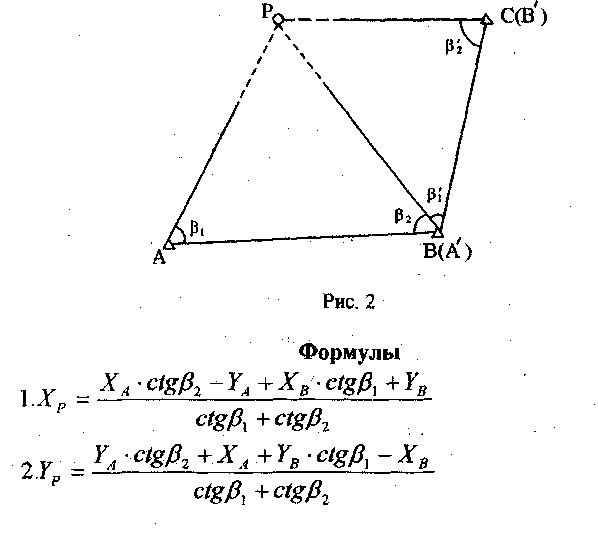





Порядок решения.

1. 
   Находят котангенсы измеренных углов β₁, β₂, 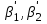, подсчитывают их
   суммы по парам и записывают в схему вычислений.
   
2. 
   Вычисляют Х_ри Y_pсначала по координатам пунктов А и В, а затем - В и С.
   
3. 
   При допустимости расхождений в координатах X_ри Y_p(до 0,20 м), по­
   лученных из двух определений, вычисляют средние арифметические значения координат пункта Р.
   

27. Прямая засечка. Формула Гаусса. Чертеж. Оценка точности.

Сущность задачи состоит в определении координат третьего пункта по координатам двух исходных и двум измеренным углам при этих пунктах. Для контроля определения измеряют еще угол при третьем исходном пункте.

В зависимости от того, какие углы измерены, задачу решают либо по формулам Юнга, либо по формулам Гаусса.

Формулы Гаусса применяют в том случае, когда между исходными пунктами А и В, В и С (рис.3) по какой - либо причине нет видимости. В этом случае измеряют углы β₁и β₂ , соответственно на пунктах А и В, а для: конт­роля правильности определения координат пункта Р - угол β₃ на пункте С меж­ду направлениями на другие пункты (К, L, N) исходной сети, на которые имеется видимость. По этим углам и дирекционным углам α_АК, α_BL, α_CNвычисляют дирекционные углы направлений на определяемый пункт α₁, α₂, α₃

Затем по координатам пунктов А и В и дирекционным углам α₁, α₂ вычисляют координаты пункта Р.

Для контроля и повышения точности окончательных результатов решают задачу второй раз по координатам пунктов В и С и дирекционным углам α₂, α₃ .



Порядок решения.

1.Находят тангенсы дирекционных углов α₁, α₂ шестью десятичными знаками после запятой и вычисляют их разности.

2.По формуле ( 1 ) вычисляют абсциссу пункта Р.

З.По формуле ( 2 ) вычисляют ординату пункта Р, проверяют вычисления по формуле ( 3 ) и записывают под значениями дирекционных углов.



4.Если координаты из двух определений расходятся между собой не более 0,20 м, то из них берут среднее арифметическое значение. Примечание : Если один из дирекционных углов близок к 90°или 270°, то значе­ния y-ков, вычисленных по формулам ( 2 ) и ( 3 ) могут сильно расходиться, тогда за окончательный результат берут тот, который получен по дирекционному углу не близкому к 90°или 270°.

Оценка точности положения определяемого пункта Р.

Сначала на миллиметровой бумаге в определенном масштабе по координатам ис­ходных пунктов А,В,С и дирекционным углам α₁, α₂, α₃ построить чертеж прямой засечки, по которому определить расстояния S₁,S₂,S₃ (в метрах). Среднюю квадратическую погрешность положения пункта Р определить по формулам: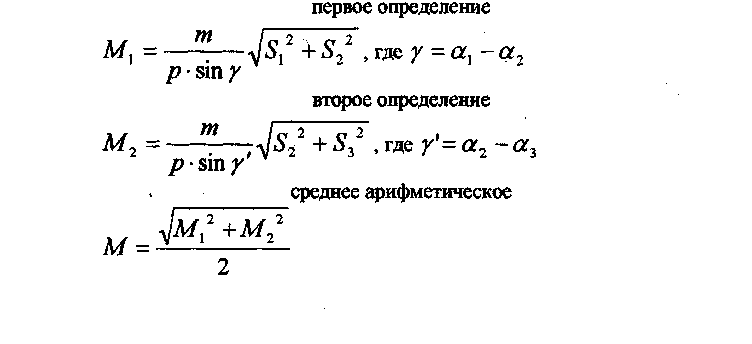



Значение средней квадратической погрешности измерения угла принять т = 5",а значение р" = 206·10³

Следует иметь ввиду что оценку точности положения определяемых пунктов обычно производят при проектировании сети на карте.

28. Обратная засечка. Чертеж. Оценка точности

Сущность обратной засечки состоит в определении координат четвертого пункта по координатам трёх исходных и двум измеренным углам при опреде­ляемом пункте.

Для решения этой задачи известно много формул. Здесь приводятся формулы Кнейссля, как наиболее экономичные для решения на микрокалькуляторах.

Решение задачи по формулам Кнейссля.

По координатам трёх исходных пунктов А, В, С и двум измеренным углам γ₁ γ₂- (рис.-4) вычислить координаты пункта Р и произвести контроль определения координат по измеренному углу s между направлениями на пункт А и четвертый исходный пункт D.





Порядок решения.

1 .Находят а = ctg γ₁ и b = ctg γ₂ с шестью десятичными знаками.

2.Вычисляют разности координат исходных пунктов, входящие в формулы (2),(3),(4) и (5 ). Последние строки для разностей Х-ов и Y-ов в схеме являются контрольными.

3 .По формулам (2),(3 ),(4),(5 ) вычисляют значения k₁,k₂, k₃, k₄, а затем величину С по формуле (6). Контролируют вычисления по формуле (7 ).

4. По формулам (8) и (9) вычисляют приращения координат ΔY_AР и ΔX_AР.

Затем находят координаты X_р, Y_pпо формулам (10) и (11).

5.По формулам (12), (13) и (14) производят контроль измерений. Значение δε не должно превышать 1’.








Оценка точности положения определяемого пункта Р.

На миллиметровой бумаге по координатам исходных пунктов А, В, С и измеренньм углам γ₁ γ₂в определённом масштабе построить чертёж засечки. По чертежу определить расстояния АВ, СВ, АР, ВР, СР (в метрах) и углы <ABC и γ_2.

Среднюю квадратическую погрешность положения определяемого пункта вычислить по формуле:



Среднюю квадратическую погрешность измерения угла принять равной m = 5”, а значение ρ = 206” • 10³.

29. Линейная засечка. Чертеж. Оценка точности.

Задача состоит в вычислении координат пункта Р по координатам пунктов А и В и измеренным расстояниям S₁иS₂от исходных пунктов до определяемого (рис.5).

В целях контроля, а также для повышения точности окончательных результатов, измеряется ещё расстояниеS₃ до третьего исходного пункта С и по координатам пунктов В и С (или А и С) и расстояниям S₂и S₃(илиS₁и S₃) вычисляют координаты пункта Р второй раз.

Формулы



*: В форлгуле (3 ) знак "+" соответствует случаю, когда пункт Р находится слева от направления АВ, а знак "—" , - когда справа.







Оценка точности положения определяемого пункта Р:

для первого определения:

для второго определения:

Принять m_S= 2 см, а углы γ и γ’определить графически по чертежу, построенному на миллиметровой бумаге.

Порядок решения.

1. 
   По формуле (1) вычисляют расстояния S и S'
   
2. 
   Вычисляют с шестью значащими цифрами значения вспомогательных
   величин q и h по формулам (2) и (3 ).
   

З.По формулам (4) и (5 ) вычисляют приращения координат ΔY_AР и ΔX_AР.

4.По формулам (6 ) и (7 ) дважды вычисляют координаты пункта Р:

а) по координатам пунктов А и В и расстояниям S₁ и S₂,

б) по координатам пунктов В и С и расстояниям S₂ и S₃. Расхождения
значений координат, полученных из двух решений не должны превышать 0,20 м. За
окончательные принимают их средние арифметические значения.
30.Лучевой метод.

Лучевой способ определения положения точек с применением электронных дальномеров разработан профессором Ю.Г. Батраковым, этим способом рекомендуется определять координаты точек в открытой всхолмленной местности, когда с пунктов триангуляции, расположенных на вершинах холмов, с земли имеется видимость по многим направлениям.

Сущность способа заключается в определении положения точек полярным способом с двух исходных пунктов - основного и дополнительного (рис.6), выбираемого рядом с основным (на расстоянии 5-20 метров от него). Координаты дополнительного пункта получают путём передачи их с основного полярным способом.

Для планового определения выбранных точек с обоих исходных пунктов (основного и дополнительного) наблюдают направления точным оптическим теодолитом и измеряют расстояния светодальномером. Проще эти измерения выполнить электронным тахеометром. Таким образом, каждую точку определяют дважды. Контролем измерений служит сходимость координат точек. В качестве окончательных принимают их средние значения.

Формулы и порядок решения здесь не приводятся, так как они известны из обработки теодолитного хода.

Все вычисления выполняют согласно образцу, приведённому в вычислительной схеме на стр.20.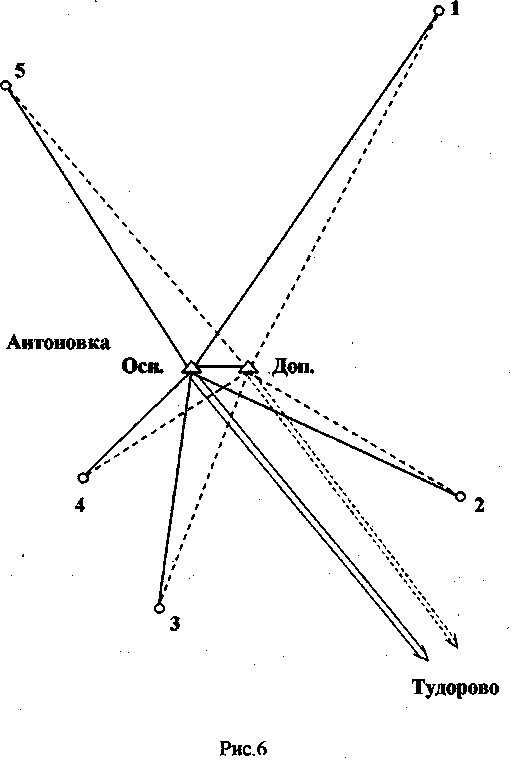






Исходные данные

Названия пунктов состояния	Дирекционный угол на п.Тудорово	Координаты
		X	Y
Антоновка осн. Антоновка доп.	133° 02' 26" 133° 03' 38"	52 478.40 52 481,55	60 743,81 60 748,06

Оценка точности положения пункта.

определяемого с основного исходного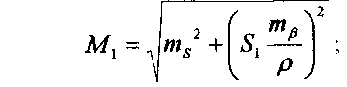



определяемого с дополнительного



среднего арифметического из двух определений



Контроль:



Для оценки точности принятьm_β=10", m_sвычислить по формуле

m_s=(10+5·10^-6S_ср)_мм

Значение S_cpвзять из таблицы, округлив до целых метров.