Ответы на билеты по геодезии (2 курс). 1. Техническая последовательность работ при тахеометрической съемке

• Название: 1. Техническая последовательность работ при тахеометрической съемке
• Дата: 03.06.2022
• Размер: 2.04 Mb.
• Имя файла: Ответы на билеты по геодезии (2 курс) .docx
• Тип: Документы; #567038
• страница: 2 из 5

Вычисление окончательного значения дирекционного угла узловой линии

№ хода
1	2	3	4	5	6	7	8	9
1 2 3

4.3.4. Прежде чем приступить к нахождению средневесового значения дирекционного угла 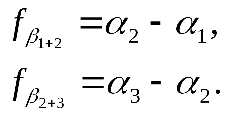 узловой линии необходимо проверить качество угловых измерений в теодолитных ходах. Для этого составляют разности вычисленных дирекционных углов и получают невязки. Первую разность составляют из дирекционных углов по двум ходам с наименьшим числом углов. Другую разность составляют из дирекционных углов, вычисленных по третьему ходу и одному из двух первых по формулам:

(4.2)

Невязки сравнивают с допустимыми значениями невязок, которые находят по формуле

, (4.3)

где  и - количество углов вi-ом и j-ом ходах.

При допустимости невязок, производят уравнивание дирекционных углов.

Определяют веса вычисленных значений дирекционных углов узловой линии по формуле

, (4.4)

где  – произвольный коэффициент, выбираемый так, чтобы веса выражались числами, близкими к единице. Веса записывают в графу 4 табл. 4.1 с округлением до 0,01.

Вычисляют средневесовое значение дирекционного угла узловой линии

, (4.5)

где  – остатки, вычисляемые по формуле

(i = 1, 2, 3). (4.6)

После этого определяют угловые невязки по всем трем ходам по значениям дирекционного угла узловой линии для правых углов по ходу

(i = 1, 2, 3) , (4.7)

а для левых углов по ходу

(i = 1, 2, 3). (4.8)

Контроль правильности вычисления дирекционного угла  и невязок проверяют по формулам

, или  .

За счет округления величины  появляется ошибка округления . Для определения следует при делении в результате удерживать две дополнительные цифры.

В этом случае контролем является выражение

[Pf] .

Если в ходе имеются и правые и левые углы, то надо изменить знак произведений Pf в столбце 8 табл. 4.1 на противоположный, чтобы все произведения соответствовали только правым или только левым углам.

4.3.5. СКП измерения угла вычисляют по формуле

, (4.9)

где  – СКП, вычисляемая по формуле

, (4.10)

где N – количество ходов.

4.3.6. Полученное окончательное значение дирекционного угла узловой линии принимают за исходное и записывают в графу "Дирекционные углы" ведомости вычисления координат.

Вычисляют теоретические суммы углов по каждому ходу, которые записывают в графу 2 ведомости вычисления координат. После этого вновь вычисляют невязки и сличают их с полученными в графе 7 табл. 4.1.

Полученные невязки распределяют с противоположным знаком поровну на углы соответствующих ходов (с округлением до 0,1´).

Для проверки правильности распределения невязок подсчитывают суммы исправленных углов. Они должны быть равны теоретическим суммам по каждому ходу.

По исправленным углам вычисляют дирекционные углы всех линий.

После этого переходят к уравниванию приращений координат.

4.3.7. Со схемы ходов выписывают в ведомость координат горизонтальные проложения сторон теодолитных ходов и координаты начальных исходных пунктов. Вычисляют приращения координат и их суммы по каждому ходу, а затем – координаты узловой точки по всем трем ходам по формулам

;  (i = 1, 2, 3). (4.11)

Результаты вычислений записывают в табл. 4.2. по вычислению окончательных значений координат узловой точки 5.

№ п/п	, м	,см	см	, см	, см		, км	k =		см	, см	см	, см	, м
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1 2 3

Для установления качества измерений длин сторон теодолитных ходов вычисляют относительные невязки по ходам: по первому вместе со вторым и по второму вместе с третьим. С этой целью составляют разности координат по соответствующим парам ходов; одна пара ходов берется с наименьшими длинами. При этом применяются следующие формулы:

;  ; (4.12)

;  ; (4.13)

;  ; (4.14)

;  , (4.15)

где  – периметрi -ого и j -того ходов;

–невязка в периметре i -ого и j -того ходов.

Значения невязок приводят в таблице 4.3.

Таблица 4.3

	S, м	Невязка
1+2 2+3

Относительные невязки не должны превышать 1:2000.

4.3.8. Выяснив, что невязки допустимы, вычисляют веса координат узловой точки

(i = 1,2,3), (4.16)

где  – длинаi–ого хода, выраженная в километрах,

k – произвольный коэффициент, выбираемый с таким расчетом, как и при вычислении дирекционных углов.

Результаты вычислений записывают в графу 9 табл. 4.2.

Затем находят средневесовое (окончательное) значение координат узловой точки

;  . (4.17)

4.3.9. По этим координатам вычисляют невязки в приращениях по каждому ходу

;  . (4.18)

Правильность вычисления средневесового значения координат узловой точки и невязок в приращениях по ходам контролируют по формулам

;  . (4.19)

За счет округления величин  и появляются ошибки округления и .

В этом случае контролирующими являются выражения

[ ] и [ ] .

4.3.10. Производят оценку точности планового положения узловой точки. Для этого:

– вычисляют СКП единицы веса

;  ; (4.20)

– вычисляют СКП абсцисс и ординат

;  ; (4.21)

– вычисляют СКП планового положения узловой точки

. (4.22)

4.3.11. Координаты узловой точки выписывают в ведомость вычисления координат и традиционным способом уравнивают приращения и вычисляют координаты точек в каждом ходе.