проектирование цилиндрического редуктора. 1 выбор электродвигателя и кинематический расчет 7 2 определение мощностей и передаваемых крутящих моментов 9
 Скачать 5.85 Mb. Скачать 5.85 Mb.
|
3.2 Расчет цилиндрической передачиИсходные данные. Частота вращения ведущего вала передачи (см. табл. 2.1): 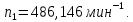 Частота вращения ведомого вала передачи (см. табл. 2.1): 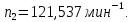 Мощность на ведущем валу передачи (см. табл. 2.1): 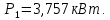 Крутящий момент на ведущем валу передачи (см. табл. 2.1): 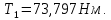 Крутящий момент на ведомом валу передачи (см. табл. 2.1): 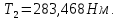 Передаточное отношение передачи (см. табл. 2.1): 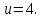 Выбор материала. Для обеспечения приблизительно одинаковой усталостной прочности зубьев шестерни и колеса рекомендуется такое сочетание материалов колес и их твердости, чтобы твердость активных поверхностей зубьев шестерни превышала твердость зубьев колеса на 25…70 НВ [2, с. 270]. По [2, с. 271, табл. 10.15] приминаем следующие материалы. Шестерня: сталь 40Х ГОСТ 4543-71, НВ 300, термообработка – улучшение. Колесо: сталь 40Х ГОСТ 4543-71, НВ 270, термообработка – улучшение. Определение допускаемых контактных напряжений. По рекомендации [2, с. 277] допускаемые контактные напряжения для расчета прямозубых и непрямозубых цилиндрических и конических передач с небольшой разностью твердостей определяются отдельно для шестерни 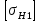 и для колеса и для колеса 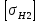 . За расчетное принимается меньшее из них. . За расчетное принимается меньшее из них.Допускаемые напряжения при расчете на контактную усталость активных поверхностей зубьев [2, с. 276, формула 10.27]: 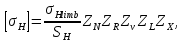 где 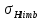 – предел контактной выносливости активных поверхностей зубьев, соответствующий базе испытаний – предел контактной выносливости активных поверхностей зубьев, соответствующий базе испытаний 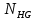 [2, с. 278, табл. 10.16]; [2, с. 278, табл. 10.16];наименьший коэффициент запаса прочности 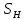 выбирается по [2, с. 278, табл. 10.16]; для материалов с равнопрочной структурой (виды термообработки: нормализация, улучшение и объемная закалка) принимается выбирается по [2, с. 278, табл. 10.16]; для материалов с равнопрочной структурой (виды термообработки: нормализация, улучшение и объемная закалка) принимается 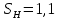 ; для материалов с неоднородной структурой (виды термообработки: поверхностная закалка, азотирование, цементация и нитроцементация с закалкой) – ; для материалов с неоднородной структурой (виды термообработки: поверхностная закалка, азотирование, цементация и нитроцементация с закалкой) – 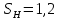 ; ;коэффициент долговечности 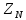 [2, с. 279, формула 10.28]: [2, с. 279, формула 10.28]: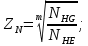 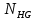 – базовое число циклов перемен напряжения; принимается по [2, с. 279, рис. 10.41] в зависимости от твердости активных поверхностей зубьев; – базовое число циклов перемен напряжения; принимается по [2, с. 279, рис. 10.41] в зависимости от твердости активных поверхностей зубьев;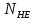 – эквивалентное число циклов перемен напряжения [2, с. 281]: – эквивалентное число циклов перемен напряжения [2, с. 281]: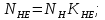 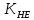 – коэффициент эквивалентности при расчете на контактную выносливость; при постоянной нагрузке – коэффициент эквивалентности при расчете на контактную выносливость; при постоянной нагрузке 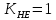 ; при переменной нагрузке, заданной типовым режимом, этот коэффициент принимается по [2, с. 282, табл. 10.17]; при переменной нагрузке, заданной циклограммой нагружения [2, с. 281]: ; при переменной нагрузке, заданной типовым режимом, этот коэффициент принимается по [2, с. 282, табл. 10.17]; при переменной нагрузке, заданной циклограммой нагружения [2, с. 281]: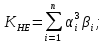 коэффициенты 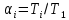 и и 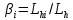 определяются по циклограмме; определяются по циклограмме;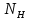 – расчетное число циклов перемены напряжений [2, с. 280, формула 10.29]: – расчетное число циклов перемены напряжений [2, с. 280, формула 10.29]: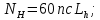 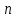 – частота вращения того из колес, по материалу которого определяется допускаемое напряжение в мин-1; – частота вращения того из колес, по материалу которого определяется допускаемое напряжение в мин-1;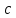 – число зацеплений зуба колеса за один оборот; – число зацеплений зуба колеса за один оборот;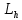 – расчетный срок службы передачи в часах (см. выше); – расчетный срок службы передачи в часах (см. выше);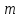 – показатель степени [2, с. 279]; при – показатель степени [2, с. 279]; при 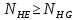 принимается принимается 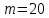 и и 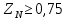 ; при ; при 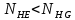 принимается принимается 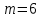 ; значение коэффициента ; значение коэффициента 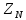 не может быть больше 2,6 при однородной структуре материала и 1,8 – при неоднородной; не может быть больше 2,6 при однородной структуре материала и 1,8 – при неоднородной;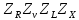 – коэффициенты, учитывающие влияние соответственно параметров шероховатости активных поверхностей зубьев, окружной скорости, вязкости смазочного материала и размеров колес; для предварительных расчетов ГОСТ 21354-87 рекомендует принимать – коэффициенты, учитывающие влияние соответственно параметров шероховатости активных поверхностей зубьев, окружной скорости, вязкости смазочного материала и размеров колес; для предварительных расчетов ГОСТ 21354-87 рекомендует принимать 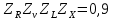 [2, с. 277]. [2, с. 277].Таким образом: 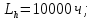 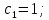 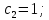 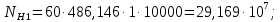 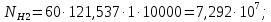 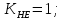 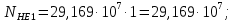 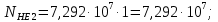 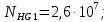 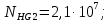 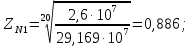 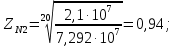 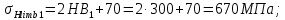 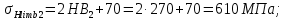 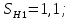 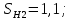 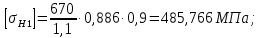 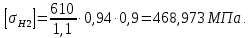 Принимаем: 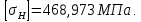 Определение допускаемых изгибных напряжений. ГОСТ 21354-87 рекомендует для проектировочных расчетов определять допускаемые напряжения изгиба по уравнению [2, с. 281]: 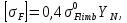 где 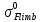 устанавливается опытным путем для отнулевого цикла в зависимости от вида термообработки [2, с. 278, табл. 10.16]; устанавливается опытным путем для отнулевого цикла в зависимости от вида термообработки [2, с. 278, табл. 10.16];коэффициент долговечности 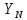 [2, с.281]: [2, с.281]: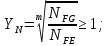 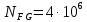 – базовое число циклов перемен напряжения [2, с. 281]; – базовое число циклов перемен напряжения [2, с. 281];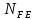 – эквивалентное число циклов перемен напряжения [2, с. 281]: – эквивалентное число циклов перемен напряжения [2, с. 281]: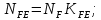 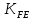 – коэффициент эквивалентности при расчете на изгибную выносливость; при постоянной нагрузке – коэффициент эквивалентности при расчете на изгибную выносливость; при постоянной нагрузке 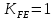 ; при переменной нагрузке, заданной типовым режимом, этот коэффициент принимается по [2, с. 282, табл. 10.17]; при переменной нагрузке, заданной циклограммой нагружения [2, с. 281, с. 276, формула 10.25]: ; при переменной нагрузке, заданной типовым режимом, этот коэффициент принимается по [2, с. 282, табл. 10.17]; при переменной нагрузке, заданной циклограммой нагружения [2, с. 281, с. 276, формула 10.25]: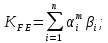 коэффициенты 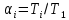 и и 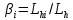 определяются по циклограмме; определяются по циклограмме;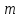 – показатель наклона левой ветви кривой усталости [2, с. 276 и с. 282, табл. 10.17]; – показатель наклона левой ветви кривой усталости [2, с. 276 и с. 282, табл. 10.17];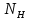 – расчетное число циклов перемены напряжений [2, с. 286, формула 10.25 и с. 281]: – расчетное число циклов перемены напряжений [2, с. 286, формула 10.25 и с. 281]: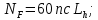 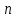 – частота вращения того из колес, по материалу которого определяется допускаемое напряжение в мин-1; – частота вращения того из колес, по материалу которого определяется допускаемое напряжение в мин-1;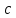 – число зацеплений зуба колеса за один оборот; – число зацеплений зуба колеса за один оборот;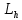 – расчетный срок службы передачи в часах (см. выше). – расчетный срок службы передачи в часах (см. выше).Таким образом: 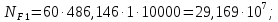 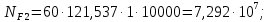 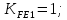 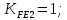 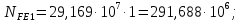 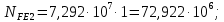 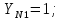 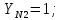 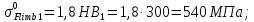 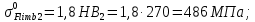 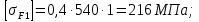 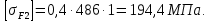 Проектировочный расчет передачи. Для предварительного определения геометрии закрытой цилиндрической передачи при не заданном межосевом расстоянии можно воспользоваться одним из двух вариантов: предварительно определить делительный диаметр шестерни [2, с. 239, формула 10.8] либо предварительно определить межосевое расстояние [2, с. 240, формула 10.9]. Т.к. межосевое расстояние лучше согласовать с ГОСТ 2185-66, то в качестве проектировочного расчета предварительно определим межосевое расстояние [2, с. 240, формула 10.9]: 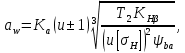 где коэффициент 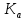 определяется по [2, с. 234, табл. 10.10]; определяется по [2, с. 234, табл. 10.10];знак «+» принимается для внешнего зацепления; «–» – для внутреннего; 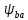 – коэффициент ширины венца относительно межосевого расстояния [2, с. 240]: – коэффициент ширины венца относительно межосевого расстояния [2, с. 240]: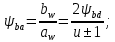 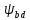 – коэффициент ширины венца относительно шестерни; принимается по [2, с. 239, табл. 10.11]; знак «+» принимается для внешнего зацепления; «–» – для внутреннего; – коэффициент ширины венца относительно шестерни; принимается по [2, с. 239, табл. 10.11]; знак «+» принимается для внешнего зацепления; «–» – для внутреннего;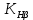 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; принимается по [2, с. 227, рис. 10.17] в зависимости от величины коэффициента – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; принимается по [2, с. 227, рис. 10.17] в зависимости от величины коэффициента 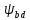 . .Таким образом: 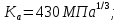 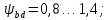 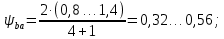 принимаем по [2, с. 239, табл. 10.11, прим. 1 – 5]: 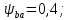 тогда: 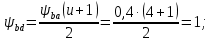 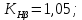 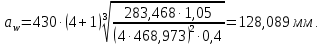 Принимаем 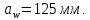 Расчет геометрии передачи. Коэффициенты смещения для обоих колес будут приняты нулевыми: 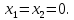 Ширина венца [2, с. 240]: 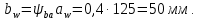 Принимаем: 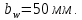 Для выбора модуля передачи можно воспользоваться следующей эмпирической зависимостью [2, с. 241]: 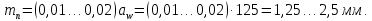 Принимаем по ГОСТ 9563-60 величину модуля: 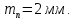 Суммарное число зубьев из формулы [2, с. 200, табл. 10.1, п.9]: 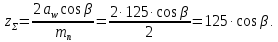 В шевронных передачах угол наклона зубьев принимают из промежутка: 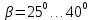 ; в косозубых – с целью ограничения осевой силы – ; в косозубых – с целью ограничения осевой силы – 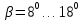 [2, с. 235]. Следует отметить, что с увеличением угла наклона, увеличивается прочность зубьев и плавность работы зацепления. [2, с. 235]. Следует отметить, что с увеличением угла наклона, увеличивается прочность зубьев и плавность работы зацепления.Также при выборе угла наклона следует учесть следующее [2, с. 231-232]. Для косозубых передач рекомендуется принимать параметры таким образом, чтобы коэффициент торцового перекрытия был 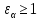 . Косозубые передачи могут удовлетворительно работать и при . Косозубые передачи могут удовлетворительно работать и при 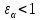 , но в этом случае необходимо, чтобы коэффициент осевого перекрытия был , но в этом случае необходимо, чтобы коэффициент осевого перекрытия был 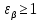 [2, с. 232]: [2, с. 232]: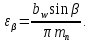 Отсюда: 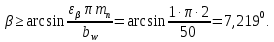 Таким образом, величина угла наклона будет выбрана из промежутка: 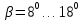 . Тогда суммарное число зубьев будет равно: . Тогда суммарное число зубьев будет равно: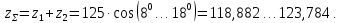 Суммарное число зубьев является целым числом. Также следует отметить, что фактическое передаточное отношение передачи равно: 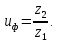 Исходя из этого, суммарное число зубьев можно выразить через число зубьев шестерни и передаточное отношение: 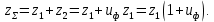 Таким образом для минимизации отклонения фактического передаточного отношения от номинального, суммарное число зубьев следует принять кратным числу: 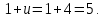 Принимаем суммарное число зубьев: 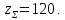 Число зубьев шестерни: 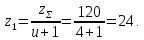 Принимаем: 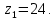 Число зубьев колеса: 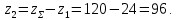 Фактическое передаточное отношение: 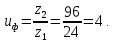 Отклонение фактического передаточного отношения от номинального: 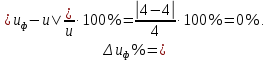 Фактическое значение передаточного числа не должно отличаться от номинального более чем на 2,5% при u≤4,5 и на 4% при u>4,5 (см. ГОСТ 2185-66, с. 2, табл. 2, прим. 3). Угол наклона линии зуба из формулы [2, с. 200, табл. 10.1, п.9]: 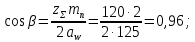 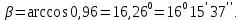 Угол главного профиля [2, с. 199]: 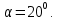 Основной угол наклона [2, с. 201, табл. 10.1, п. 18]: 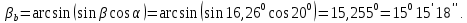 Делительные диаметры колес без смещения [2, с. 200, табл. 10.1, п. 10]: 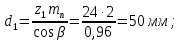 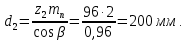 Проверка межосевого расстояния: 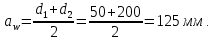 Диаметры вершин зубьев колес без смещения: 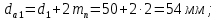 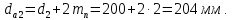 Диаметры впадин зубьев колес без смещения: 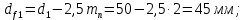 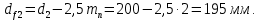 Угол профиля [2, с. 200, табл. 10.1, п. 7]: 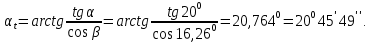 Угол зацепления равен углу профиля, т.к. суммарное смещение равно нулю [2, с. 202, табл. 10.1, прим. 2]: 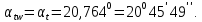 Основные диаметры колес [2, с. 201, табл. 10.1, п. 20]: 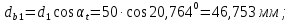 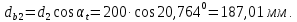 Углы профиля зуба в точках на окружностях вершин колес [2, с. 201, табл. 10.1, п. 20]: 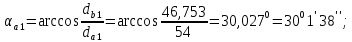 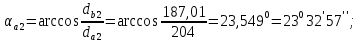 Осевой шаг [2, с. 201, табл. 10.1, п. 23]: 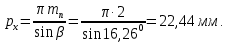 Окружной шаг [2, с. 201, табл. 10.1, п. 24]: 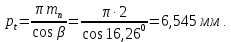 Коэффициент торцового перекрытия [2, с. 231]: 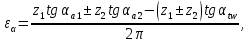 здесь знак «+» используется для внешнего зацепления, «–» – для внутреннего. 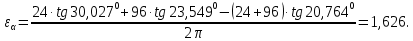 Коэффициент осевого перекрытия [2, с. 201, табл. 10.1, п. 26]: 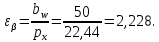 Коэффициент перекрытия [2, с. 201, табл. 10.1, п. 27]: 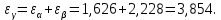 Окружная скорость передачи [2, с. 230]: 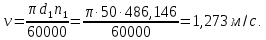 По [2, с. 211, табл. 10.4] принимаем степень точности передачи 9. Вид сопряжения колес – В [2, с. 213]. Проверочный расчет на контактную усталость активных поверхностей. Критерий контактной прочности передачи [2, с. 238, формула 10.7]: 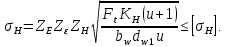 Допускается недогрузка/перегрузка ±5% [2, с. 241]. Значение 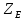 принимается по [2, с. 234, табл. 10.10]. принимается по [2, с. 234, табл. 10.10].Коэффициент, учитывающий суммарную длину контактных линий; принят для 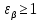 [2, с. 238]: [2, с. 238]: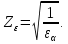 Коэффициент, учитывающий форму сопряженных поверхностей зубьев [2, с. 238]: 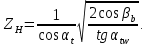 Окружная сила в зацеплении [2, с. 238]: 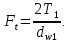 Коэффициент нагрузки при расчете на контактную прочность [2, с. 222]: 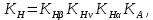 где 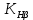 – коэффициент, учитывающий распределение нагрузки по ширине венца (см. выше); – коэффициент, учитывающий распределение нагрузки по ширине венца (см. выше);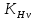 – коэффициент, учитывающий внутреннюю динамику передачи; определяется в зависимости от окружной скорости, степени точности по нормам плавности твердости рабочих поверхностей зубьев [2, с. 229]: – коэффициент, учитывающий внутреннюю динамику передачи; определяется в зависимости от окружной скорости, степени точности по нормам плавности твердости рабочих поверхностей зубьев [2, с. 229]: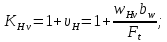 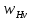 – удельная окружная динамическая сила [2, с. 229]: – удельная окружная динамическая сила [2, с. 229]: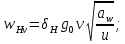 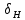 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля головок зубьев; принимается по [2, с. 230, табл. 10.7] в зависимости от твердости поверхности зубьев и вида зубьев; – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля головок зубьев; принимается по [2, с. 230, табл. 10.7] в зависимости от твердости поверхности зубьев и вида зубьев;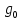 – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса; принимается по [2, с. 230, табл. 10.8] в зависимости от величины модуля и степени точности; – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса; принимается по [2, с. 230, табл. 10.8] в зависимости от величины модуля и степени точности;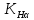 – коэффициент, учитывающий распределение нагрузки между зубьями; определяется по [2, с. 231, табл. 10.9] в зависимости от окружной скорости и степени точности; – коэффициент, учитывающий распределение нагрузки между зубьями; определяется по [2, с. 231, табл. 10.9] в зависимости от окружной скорости и степени точности;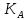 – коэффициент, учитывающий внешнюю динамическую нагрузку; принимается равным единице, если в задании нет дополнительных условий. – коэффициент, учитывающий внешнюю динамическую нагрузку; принимается равным единице, если в задании нет дополнительных условий.Таким образом: 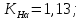 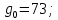 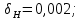 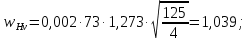 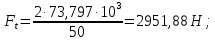 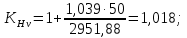 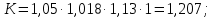 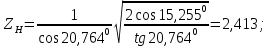 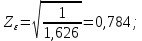 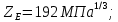 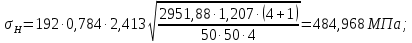 Недогрузка/перегрузка по контактным напряжениям составляет: 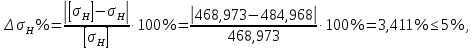 что допустимо. Контактная прочность обеспечена. Расчет на прочность при изгибе. Критерий прочности зубьев при расчете на изгиб [2, с. 247, формула 10.13]: 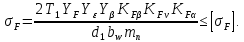 Произведя замену: 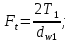 получим: 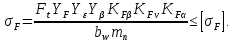 Допускаемые напряжения 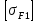 и и 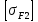 чаще всего различаются, как и коэффициенты чаще всего различаются, как и коэффициенты 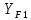 и и 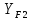 , поскольку они зависят от числа зубьев и коэффициента смещения. Поэтому проверку изгибной прочности следует проводить отдельно для шестерни и колеса. В уравнения нужно подставить меньшее из отношений , поскольку они зависят от числа зубьев и коэффициента смещения. Поэтому проверку изгибной прочности следует проводить отдельно для шестерни и колеса. В уравнения нужно подставить меньшее из отношений 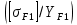 и и 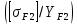 , т.е. расчет производить по менее прочному зубу [2, с. 248]. , т.е. расчет производить по менее прочному зубу [2, с. 248].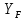 – коэффициент, учитывающий влияние формы зуба и концентрации напряжений; принимается по [2, с. 246, рис. 10.24] в зависимости от эквивалентного числа зубьев – коэффициент, учитывающий влияние формы зуба и концентрации напряжений; принимается по [2, с. 246, рис. 10.24] в зависимости от эквивалентного числа зубьев 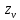 . .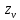 – эквивалентное число зубьев [2, с. 207]: – эквивалентное число зубьев [2, с. 207]: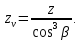 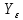 – коэффициент, учитывающий перекрытие зубьев [2, с. 247]; для прямозубых и косозубых передач при – коэффициент, учитывающий перекрытие зубьев [2, с. 247]; для прямозубых и косозубых передач при 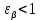 принимают: принимают: 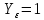 ; для косозубых колес при ; для косозубых колес при 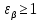 : :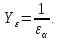 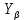 – коэффициент, учитывающий наклон зуба [2, с. 247]: – коэффициент, учитывающий наклон зуба [2, с. 247]: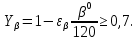 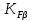 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; принимается по [2, с. 227, рис. 10.17] в зависимости от величины – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; принимается по [2, с. 227, рис. 10.17] в зависимости от величины 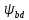 [2, с. 246]. [2, с. 246].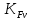 – коэффициент, учитывающий внутреннюю динамику передачи; определяется в зависимости от окружной скорости, степени точности по нормам плавности твердости рабочих поверхностей зубьев [2, с. 229]: – коэффициент, учитывающий внутреннюю динамику передачи; определяется в зависимости от окружной скорости, степени точности по нормам плавности твердости рабочих поверхностей зубьев [2, с. 229]: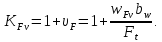 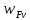 – удельная окружная динамическая сила [2, с. 230]: – удельная окружная динамическая сила [2, с. 230]: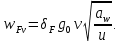 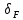 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля головок зубьев; принимается по [2, с. 230]. – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля головок зубьев; принимается по [2, с. 230].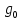 – коэффициент, учитывающий влияние разности шагов зубьев шестерни и колеса; принимается по [2, с. 230, табл. 10.8]. – коэффициент, учитывающий влияние разности шагов зубьев шестерни и колеса; принимается по [2, с. 230, табл. 10.8].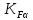 – коэффициент, учитывающий распределение нагрузки между зубьями; для прямозубых и косозубых передач при – коэффициент, учитывающий распределение нагрузки между зубьями; для прямозубых и косозубых передач при 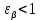 принимают принимают 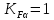 [2, с. 246]; для косозубых при [2, с. 246]; для косозубых при 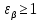 , значение , значение 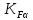 принимается по [2, с. 231, табл. 10.9] в зависимости от окружной скорости и степени точности. принимается по [2, с. 231, табл. 10.9] в зависимости от окружной скорости и степени точности.Таким образом: 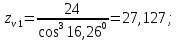 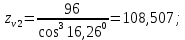 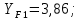 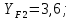 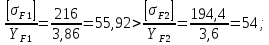 проверяем прочность зубьев колеса; 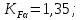 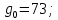 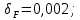 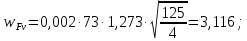 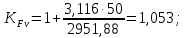 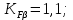 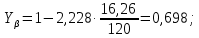 принимаем 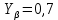 ; ;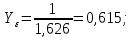 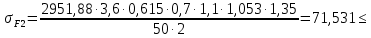 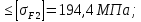 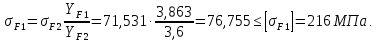 Изгибная прочность зубьев обеспечена. Расчет сил в зацеплении. Окружная сила была рассчитана выше: 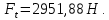 Радиальная сила [2, с. 235]: 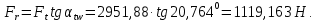 Осевая сила [2, с. 235]: 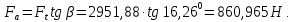  Рисунок 3.2.1 – Схема цилиндрической передачи без смещения 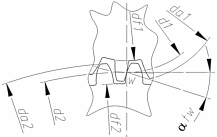 Рисунок 3.2.2 – Схема цилиндрического зацепления без смещения Таблица 3.2.1 – Сводная таблица данных расчета цилиндрической косозубой передачи
|

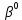 =16015’37’’
=16015’37’’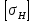 = 468,973 МПа
= 468,973 МПа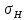 = 484,968 МПа
= 484,968 МПа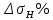 = 3,411%
= 3,411%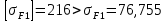 МПа
МПа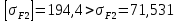 МПа
МПа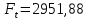 Н
Н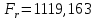 Н
Н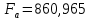 Н
Н