жд путь. 1. Выбор конструкции верхнего строения пути
 Скачать 2.19 Mb. Скачать 2.19 Mb.
|
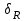 точки изменения радиуса точки изменения радиуса 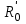 на на 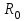 определяется по формуле: определяется по формуле: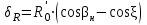 , (3.8) , (3.8)Произведем расчет по формулам (3.4) – (3.8) для данного варианта задания. 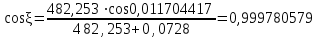 ; ;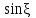 =0,020947407; =0,020947407;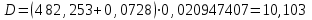 м; м;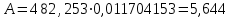 м; м;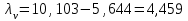 м; м;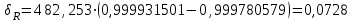 м. м.3.1.3. Длина криволинейного остряка, полный стрелочный угол и ордината в корне остряка. Для определения длины криволинейного остряка схемой, изображенной на рисунке 3.3. 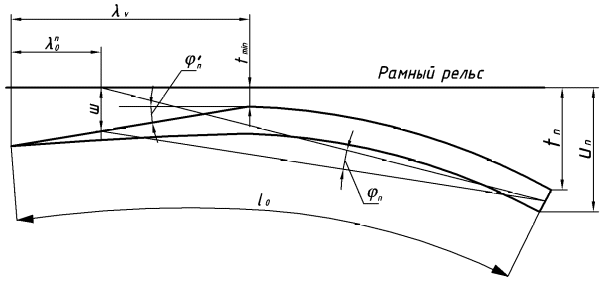 Рисунок 3.3 – Схема к определению длины криволинейного остряка Выведем формулу для определения длины криволинейного остряка. φп=φп’; sin φп=sin φп’= 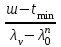 ; (3.9) ; (3.9)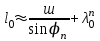 ; (3.10) ; (3.10)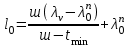 ; (3.11) ; (3.11)примем ш = 147 мм, 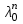 = 360 мм, = 360 мм, 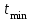 = 71 мм, тогда = 71 мм, тогда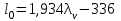 , мм. (3.12) , мм. (3.12)Определим численное значение длины криволинейного остряка: 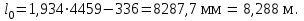 Полный стрелочный угол и ординату в корне остряка определим следующим образом: 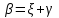 ; (3.13) ; (3.13)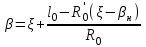 ; (3.14) ; (3.14) 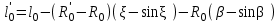 ; (3.15) ; (3.15)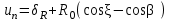 . (3.16) . (3.16)Перечисленные выше характеристики показаны на рисунке 3.4. 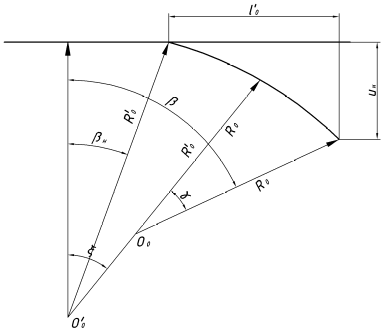 Рисунок 3.4 – Схема к определению полного стрелочного угла и ординаты в корне остряка Определим численные значения параметров стрелки по формулам (3.14) – (3.16). 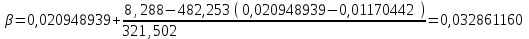 ; ;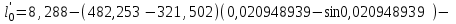 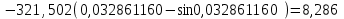 м; м;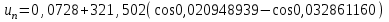 =0,176 м. =0,176 м.3.2. Основные параметры жесткой крестовины К основным параметрам крестовины относятся: α – угол крестовины; 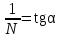 – марка крестовины; – марка крестовины;n – передний вылет крестовины; m – задний вылет крестовины. 3.2.1. Угол крестовины и ее марка 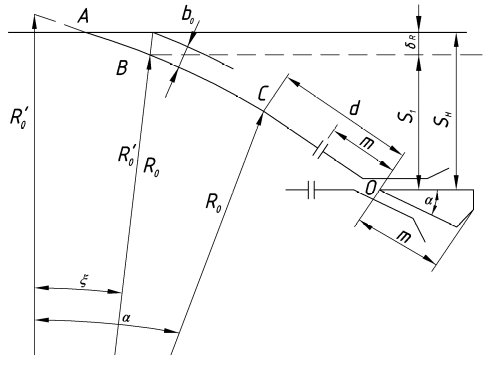 Рисунок 3.5 – Схема к определению марки крестовины Угол крестовины α может быть определен из уравнения проекции расчетного контура АВСО, показанного на рисунке 3.5, по формуле 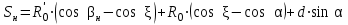 , (3.17) , (3.17)где d – величина прямой вставки перед центром крестовины, мм. 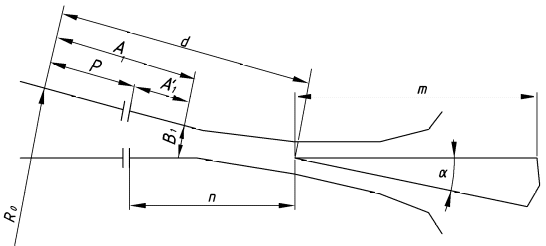 Рисунок 3.6 – Схема к определению длины прямой вставки 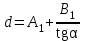 , (3.18) , (3.18)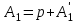 , (3.19) , (3.19)где 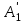 и и 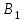 – величины, зависящие от конструктивных характеристик крестовины, согласно [1, табл. 3.1] примем – величины, зависящие от конструктивных характеристик крестовины, согласно [1, табл. 3.1] примем 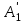 =316 мм, =316 мм, 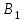 =283 мм; =283 мм;p – размер прямой вставки между концом переводной кривой и передним стыком крестовины, примем равным 1000 мм. Тогда 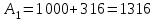 мм. мм.Преобразуем уравнение (3.17), зная что 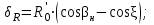 (3.20) (3.20)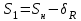 , (3.21) , (3.21)где 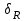 – ордината точки перехода очертания остряка с радиуса – ордината точки перехода очертания остряка с радиуса 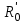 к к 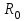 . .Для данного варианта задания 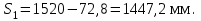 Учитывая вышеизложенное, выражение (3.17) запишем в виде: 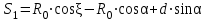 . (3.22) . (3.22)Подставив в выражение (3.22) зависимость (3.18) и сделав преобразования, будем иметь: 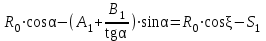 . (3.23) . (3.23)Обозначим правую часть уравнения через C: 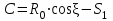 . (3.24) . (3.24)Для данного варианта задания 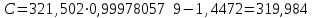 м. м.Выражение (3.24) несколько преобразуем: 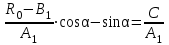 . .Примем  Подставив формулу (3.25) в преобразованное выражение (3.24), получим:  Подставив значение А1 из выражения (3.25) в формулу (3.26), получим:  Значение угла 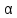 определим по следующему выражению: определим по следующему выражению: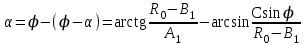 . (3.28) . (3.28)Определим это значение для данного варианта задания: 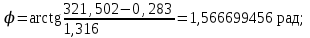 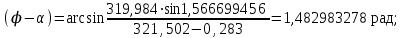 α =1,566699456 – 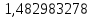 = 0,083716178 рад. = 0,083716178 рад.Знаменатель марки крестовины N определяется по выражению: 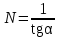 . (3.29) . (3.29)Тогда 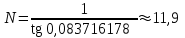 . .Осуществим проверку правильности расчетов по формуле: R0cosξ – R0cosα + dsinα + δR = 1520 мм. 321,502cos 0,020949369 – 321,502cos0,083716178 + 4,689sin0,083716178 + 0,0728 = = 1520,3 мм. Так как произвели округление марки крестовины, то необходимо пересчитать угол крестовины и размер прямой вставки: 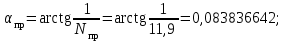 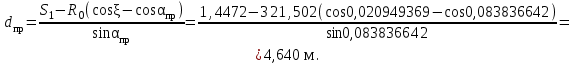 Произведем проверку найденных значений: Sн = δR + R0(cosξ – cosαпр) + dпрsinαпр = 0,0728 + 321,502∙ ∙ 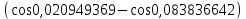 + 4,640sin0,083836642 = 1520,45 мм. + 4,640sin0,083836642 = 1520,45 мм.3.2.2. Основные размеры крестовины 3.2.2.1. Минимальная длина сборной крестовины с литым сердечником 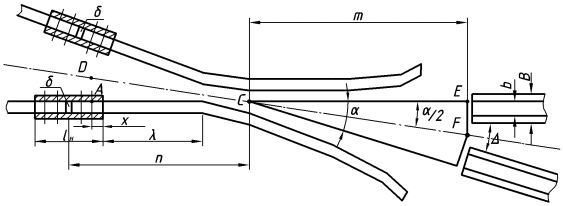 Рисунок 3.7 – Схема к определению длины сборной крестовины Крестовина, схема которой изображена на рисунке 3.7, состоит из передней (усовой) и хвостовой частей. Длина крестовины lk будет равна: lk = m + n, (3.30) где m – длина хвостовой части крестовины; n – длина передней части крестовины. Эти расстояния, в свою очередь, определяются следующим образом: n = CA + 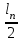 – х1 – – х1 – 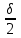 , (3.31) , (3.31)где CA = 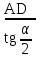 ; AD = ; AD = 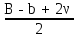 . (3.32) . (3.32)Тогда n = 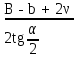 + + 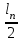 – х1 – – х1 – 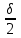 . (3.33) . (3.33)Допуская, что 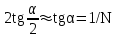 , будем иметь , будем иметьn = 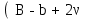 )N + 0,5 )N + 0,5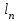 – х1 – – х1 – 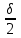 , (3.34) , (3.34)где B – ширина подошвы рельса, мм; b – ширина головки рельса, мм; 2 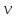 – расстояние между подошвами усовиков крестовины в месте установки первого болта в переднем стыке крестовины, мм, принимается из условия свободной постановки болта и зависит от его длины и зазоров, мм; – расстояние между подошвами усовиков крестовины в месте установки первого болта в переднем стыке крестовины, мм, принимается из условия свободной постановки болта и зависит от его длины и зазоров, мм;lн – длина накладки, мм; х1 – расстояние от торца накладки до оси первого болтового отверстия, мм; 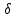 – величина стыкового зазора, принимается 0 мм. – величина стыкового зазора, принимается 0 мм.По рисунку 3.7 видно, что из треугольника CEF CE = m = 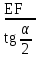 , (3.35) , (3.35)где EF = 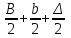 . . Тогда m = 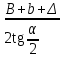 , (3.36) , (3.36)или m = (B + b + 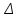 )N )Nгде 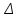 = 5 мм – зазор между подошвами рельсов, примыкающих к сердечнику. = 5 мм – зазор между подошвами рельсов, примыкающих к сердечнику.Данные для расчета элементов крестовины приведены в [1, табл. 3.2]. По формулам (3.34) и (3.36) определим значения элементов крестовины для данного варианта задания. n = 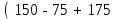 )11,9 + 0,5·800 – 80 – )11,9 + 0,5·800 – 80 – = 3295 мм = 3,295 м; = 3295 мм = 3,295 м;m = (150 + 75 + 5)11,9 = 2737 мм = 2,737 м; lk = 3,295 + 2,737 = 6,032 м. 3.2.2.2. Практическая длина крестовины  Рисунок 3.8 – Раскладка брусьев под крестовиной Практическую длину определим исходя из равномерного распределения брусьев под крестовиной, данная схема представлена на рисунке 3.8. При этом необходимо соблюсти ряд условий: 1. Пролёты между осями шпал должны составлять на прямых участках 545-547 мм, а на кривых радиусом менее 1200 м – 501-502 мм. 2. Брусья под крестовиной располагаются так, чтобы сечение сердечника, размером 20мм находилось в середине пролёта. 3. Брусья под крестовиной укладывают перпендикулярно биссектрисе угла α. Сечение сердечника размером 20мм находится на расстоянии f от центра крестовины и составляет: 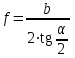 ; (3.37) ; (3.37)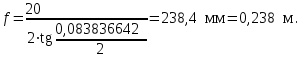 Найдем проекции величин m и n на биссектрису угла α: 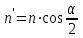 ; (3.38) ; (3.38)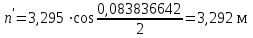 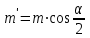 (3.39) (3.39)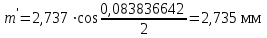 Ось первого бруса от переднего стыка крестовины располагается на расстоянии H: 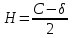 , (3.40) , (3.40)где С – стыковой пролёт (для рельсов Р65 С = 420мм); δ – стыковой зазор (примем δ = 0 мм). Тогда 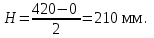 Для распределения брусьев под передней частью крестовины найдем расстояние ED: ED = n’ – H + f – 0,5a (3.41) где а – величина пролёта (примем а = 500 мм). Тогда ED = 3,292 – 0,21 + 0,238 – 0,5·0,5 = 3,07 м. Отсюда число пролётов на этом участке будет равно: 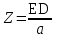 ; (3.42) ; (3.42)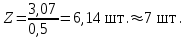 Так как Z удлинилась в большую сторону, то фактическая длина передней части крестовины: 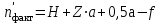 ; (3.43) ; (3.43)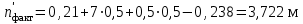 . .Отсюда найдем практическое значение передней части крестовины: 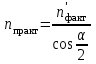 ; (3.44) ; (3.44)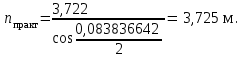 Аналогично определим длину хвостовой части крестовины: DF = m’ – H – f + 0,5a; (3.45) DF = 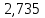 – 0,21 – 0,238 + 0,5·0,5 = 2,537 мм; – 0,21 – 0,238 + 0,5·0,5 = 2,537 мм;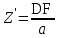 ; (3.46) ; (3.46)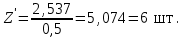 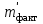 = H + Z ’·a + f – 0,5a; (3.47) = H + Z ’·a + f – 0,5a; (3.47)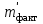 = 0,21 + 6·0,5 + 0,238 – 0,5·0,5 = 3,198 м; = 0,21 + 6·0,5 + 0,238 – 0,5·0,5 = 3,198 м;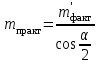 ; (3.48) ; (3.48)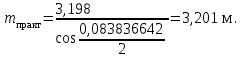 Длина крестовины: 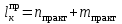 (3.49) (3.49)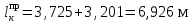 . .3.3. Геометрические характеристики крестовины и контррельсов 3.3.1. Длина усовиков крестовины 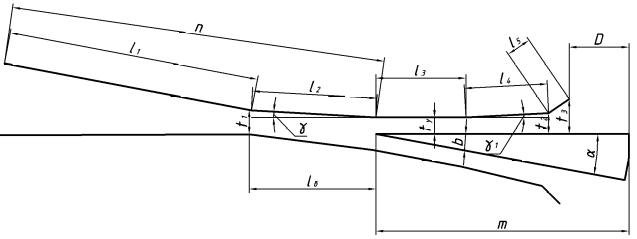 Рисунок 3.9 – Схема к определению длины усовика Развернутую длину усовиков крестовины, изображенных на рисунке 3.9, определяют из следующего выражения: lус = l1 + l2 + l3 + l4 + l5; (3.50) 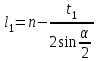 , (3.51) , (3.51)где n – длина передней (усовой) части крестовины; t1 – ширина желоба в горле крестовины, принимается равной 62 мм; α – угол крестовины; 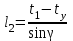 , (3.52) , (3.52)где γ – угол отгиба усовика крестовины в пределах вредного пространства, одновременно являющийся и углом удара колеса в усовик крестовины при движении экипажа по прямому пути от стрелки к крестовине. Величина угла 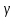 может быть определена по формуле: может быть определена по формуле: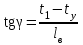 , (3.53) , (3.53)где  – ширина желоба в прямой части усовиков, принимается равной 46 мм; – ширина желоба в прямой части усовиков, принимается равной 46 мм;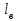 – длина вредного пространства или проекция отрезка усовика l2 на направление рабочей грани рельса прямого пути, определяемая по формуле: – длина вредного пространства или проекция отрезка усовика l2 на направление рабочей грани рельса прямого пути, определяемая по формуле: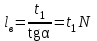 . (3.54) . (3.54)Длину участка l3 определяют при условии, что ширина желоба, равная 46 мм, сохраняется от математического центра крестовины до той точки сердечника, где его сечение b равняется 50 мм: l3 = 50N, (3.55) Длину участка l4 определяют по формуле: |
