Шпаргалки для Деталей Машин. 1. Виды разрушения ремней. Расчет ременных передач по тяговой способности и на долговечность. Перегрев ремня
 Скачать 6.03 Mb. Скачать 6.03 Mb.
|
где F – сила, действующая на заклепку, [ ср] - допускаемое напряжение заклепок на срез, k – число плоскостей среза в соединении, d – диаметр стержня заклепки, [ см] - допускаемое напряжение заклепок на смятие, n – количество заклепок (в односрезных заклепках n = k), s – наименьшая толщина соединяемых частей, [ р] - допускаемое напряжение на отрыв головок.10.Муфты. Классификация муфт по принципу действия и характеру работы. Постоянные муфты и их расчет Муфтой называется устройство для соединения валов. Основное назначение муфт- передача вращающего момента между валами, без изменения его значения и направления. Кроме передачи момента, некоторые муфты выполняют дополнительные функции. Классификация муфт По конструкции: Управляемые (сцепные, автоматические) Неуправляемые (постоянно действующие) По назначению: Жесткие (глухие) муфты - для постоянного неразрывного соединения валов. Самый распространенный вид муфт. Компенсирующие муфты - компенсируют смещение валов Упругие муфты - компенсируют динамические нагрузки. Основная часть этих муфт - упругий элемент, которые передает вращающий момент от одной полумуфты к другой Сцепные муфты - соединяют или разъединяют валы с деталями. Служат для быстрого соединения /разъединения валов при работающем двигателе. Применяютя при строгой соосноссти валов. Они должны легко и быстро включаться при незначительной силе, а также иметь малый нагрев, и небольшую изнашиваемость при частых переключениях. Самоуправляемые (автоматические) муфты - срабатывают сами при определенных условиях Электромагнитные и магнитные-Электромагнитные муфты применяют для замыкания и размыкания цепей без прекращения вращения, а также для регулирования движения приводов станков. Муфты подбирают в зависимости от расчетного крутящего момента Мр, при определении которого необходимо учитывать вид двигателя, величину масс, деталей, соединенных с муфтой, и степень неравномерности их вращения. Величину расчетного момента приближенно рекомендуется определять по формуле Мр = (К1+К2)М < Мкр, где М —длительно действующий крутящий момент, передаваемый муфтой; К1— коэффициент, зависящий от вида двигателя; К2 — коэффициент, учитывающий величину ускоряемых масс и степень равномерности их вращения; Мкр — наибольший крутящий момент, допускаемый для данного типоразмера муфты. При заданных мощности и частоте вращения момент М = 974 N/n, кгс • м, где N — передаваемая мощность, кВт; n — частота вращения, об/мин. 11) Напряжения в ремне. Эпюра напряжений в ремне при работе передачи. 1.Напряжение σ0 от силы предварительного натяжения.  2.Полезное напряжение στ. Отношение окружной силы (полезной нагрузки) Fτ к площади поперечного сечения А называют полезным напряжением στ: στ = Fτ/A. Так как Fτ = F1-F2, то полезное напряжение στ , является разностью напряжений в ведущей σ1 , и ведомой σ2 ветвях ремня при рабочем ходе на малой скорости (пока не сказывается влияние центробежных сил), т. е. στ = σ1-σ2. 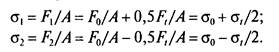 Величина στ определяет тяговую способность ременной передачи.  3. Напряжение изгиба σи возникает в ремне при огибании им шкивов. В местах набегания ремня на шкивы и сбегания ремня не происходит резких скачков напряжений (см. рис. 22.6), так как радиус кривизны ремня изменяется постепенно. 3. Напряжение изгиба σи возникает в ремне при огибании им шкивов. В местах набегания ремня на шкивы и сбегания ремня не происходит резких скачков напряжений (см. рис. 22.6), так как радиус кривизны ремня изменяется постепенно.4. Напряжение от центробежной силы Fv Влияние σv на работоспособность ременной передачи при v<25 м/с незначительно. Наибольшее напряжение Напряжение изгиба обычно значительно превышает все другие составляющие наибольшего напряжения. М 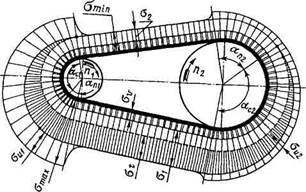 аксимальное напряжение действует в поперечном сечении ремня в месте его набегания на малый шкив и сохраняет свою величину на всей дуге покоя ап1 . аксимальное напряжение действует в поперечном сечении ремня в месте его набегания на малый шкив и сохраняет свою величину на всей дуге покоя ап1 .Эпюра напряжений в ремне при работе передачи 12) , 19)Оси и валы. Расчет осей и валов. . Расчет валов на сопротивление усталости и на жесткость. Вал предназначен для поддержания размещенных на нем зубчатых колес, шкивов, звездочек и других деталей машин, а также для передачи крутящего момента. Некоторые валы (гибкие, карданные,торсионные) не поддерживают вращающиеся детали. При работе вал испытывает изгиб и кручение, а иногда дополнительно растяжение и сжатие. Ось предназначена лишь для поддержания размещенных на ней деталей и подвергается только изгибу. В отличие от вала ось не передает крутящий момент. Оси могут быть неподвижными или вращающимися.  Проектный расчет валов. Проектный расчет производится только на кручение, причем для компенсации напряжений изгиба и других неучтенных факторов принимают значительно пониженные значения допускаемых напряжений кручения, например для выходных участков  валов редукторов [к] = (0,025–0,03) σв, где σв – временное сопротивление материала вала. Тогда диаметр вала определится как валов редукторов [к] = (0,025–0,03) σв, где σв – временное сопротивление материала вала. Тогда диаметр вала определится какгде Тк – крутящий момент, возникающий в расчетном сечении вала и обычно численно равный передаваемому вращающему моменту Т; [`к] – допускаемое напряжение на кручение. Для валов из сталей Ст5, Ст6, 45 принимают: при определении диаметра выходного конца к τ = 20–25 МПа; при определении диаметра промежуточного вала под шестерней к τ = 10–20 МПа. Полученное значение диаметра округляют до ближайшего стандартного. При проектировании редукторов диаметр выходного конца быстроходного вала часто принимают равным (или почти равным) диаметру вала электродвигателя, с которым он будет соединен муфтой. После установления диаметра выходного конца вала назначается диаметр цапф вала (несколько больше диаметра выходного конца) и производится подбор подшипников. Диаметр посадочных поверхностей валов под ступицы насаживаемых деталей для удобства сборки принимают больше диаметров соседних участков. В результате этого ступенчатый вал по форме оказывается близок к брусу равного сопротивления. После разработки конструкции вала и компоновки узла выполняют проверочные расчеты, основным из которых является расчет на сопротивление усталости, дополняемый в некоторых случаях расчетами на статическую прочность, жесткость и колебания. Проверочный расчет на сопротивление усталости. Упрощенный проверочный расчет валов на усталость исходит из предположения, что не только нормальные, но и касательные напряжения изменяются по симметричному (наиболее неблагоприятному) циклу. Этотвид расчета дает неточность на несколько процентов в сторону увеличения запаса прочности вала. Условие сопротивления усталости имеет Вид 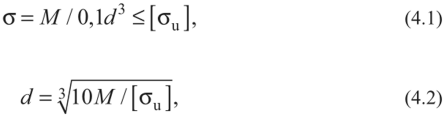 где σэкв – эквивалентное напряжение в проверяемом сечении; Mэкв – эквивалентный момент; d – диаметр вала в этом сечении; [σ-1и] – допускаемое напряжение на изгиб при симметричном цикле изменения напряжений. Расчетный диаметр вала в проверяемом сечении определяется по формуле и сравнивается с принятым при конструировании вала диаметром. Если проверяемое сечение вала ослаблено шпоночной канавкой, то расчетный диаметр вала следует увеличить на 7–10 %. Приведенные для проектного и проверочного расчета валов формулы и рекомендации используются и для расчета осей с учетом только нормальных напряжений изгиба, так как Т = 0. Уточненный проверочный расчет валов на усталость исходит из предположения, что нормальные напряжения изменяются по симметричному, а касательные – по асимметричному циклу. Этот расчет заключается в определении фактического коэффициента запаса прочности в предположительно опасных сечениях с учетом характера изменения напряжений, влияния абсолютных размеров деталей, концентрации напряжений, шероховатости и упрочнения поверхностей и проводится в следующей последовательности: 1. Определяют силы, действующие на шкивы, зубчатые колеса и т. д. 2. Если силы действуют в разных плоскостях, то их раскладывают на вертикальные и горизонтальные составляющие. 3. В двух взаимно-перпендикулярных плоскостях определяют опорные реакции. 4. В двух взаимно – перпендикулярных плоскостях строят эпюры изгибающих моментов. 69 5 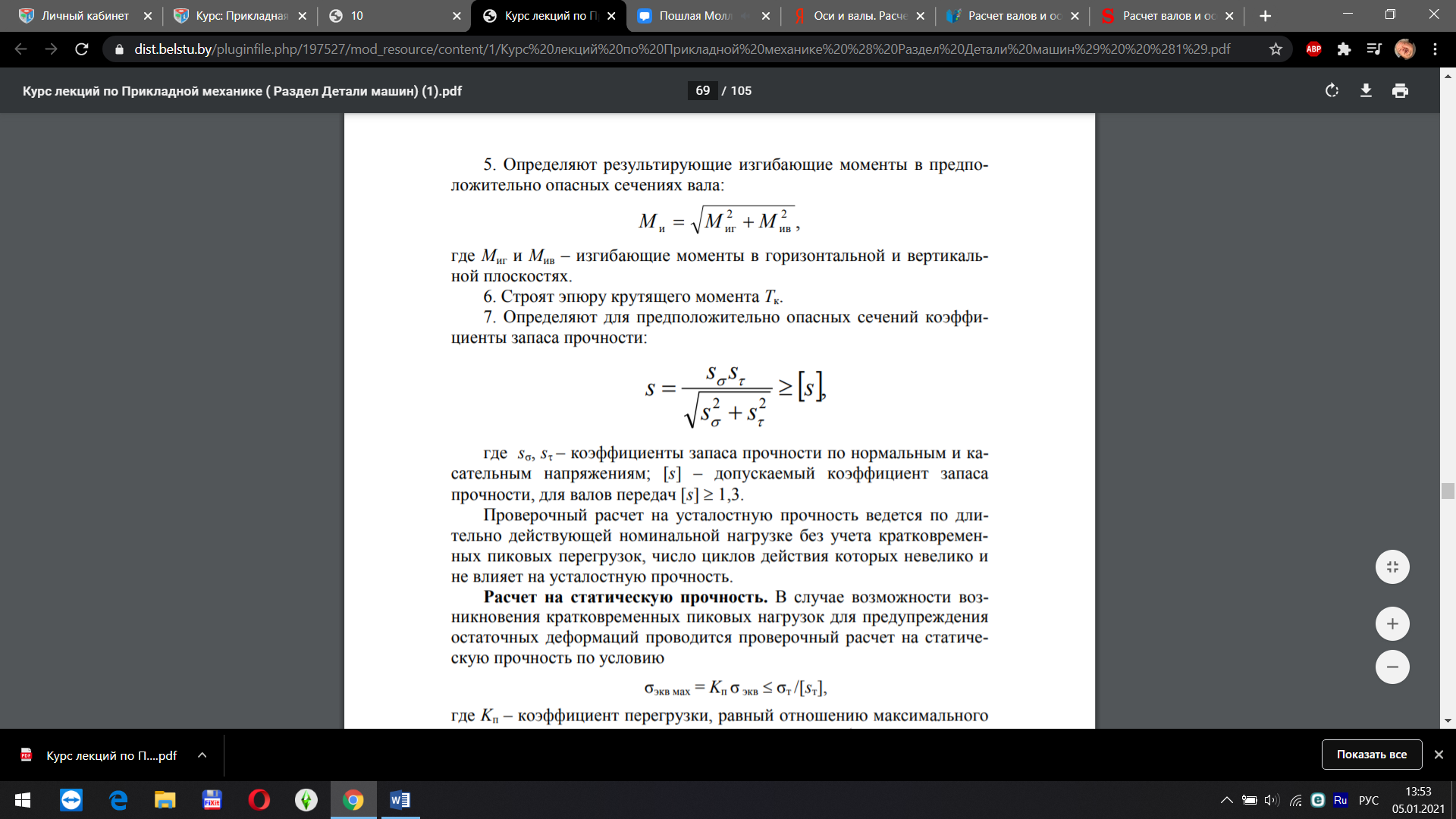 . Определяют результирующие изгибающие моменты в предположительно опасных сечениях вала: . Определяют результирующие изгибающие моменты в предположительно опасных сечениях вала: где Миг и Мив – изгибающие моменты в горизонтальной и вертикальной плоскостях. 6. Строят эпюру крутящего момента Тк. 7  . Определяют для предположительно опасных сечений коэффициенты запаса прочности: . Определяют для предположительно опасных сечений коэффициенты запаса прочности:где sσ, [s]– коэффициенты запаса прочности по нормальным и касательным напряжениям; [s] – допускаемый коэффициент запаса прочности, для валов передач [s] >=1,3. Проверочный расчет на усталостную прочность ведется по длительно действующей номинальной нагрузке без учета кратковременных пиковых перегрузок, число циклов действия которых невелико и не влияет на усталостную прочность. Расчет на статическую прочность. В случае возможности возникновения кратковременных пиковых нагрузок для предупреждения остаточных деформаций проводится проверочный расчет на статическую прочность по условию  где Kп – коэффициент перегрузки, равный отношению максимального момента двигателя к его номинальному значению (при наличии предохранительного устройства Kп зависит от момента, при котором срабатывает это устройство); σт – предел текучести материала; [sт] – допускаемый коэффициент запаса прочности по пределу текучести. Обычно принимают [sт] = 1,2–1,8.  Расчет валов и осей на жесткость. Расчет валов и осей на жесткость.Под действием приложенных активных и реактивных сил валы изгибаются и скручиваются. Максимальный прогиб вала или оси называется стрелой прогиба и обозначается через f. Деформация кручения вала характеризуется углом закручивания В результате прогиба и поворота сечений вала изменяется взаимное положение зубчатых венцов передач и элементов подшипников, что вызывает неравномерность распределения нагрузок по ширине венцов зубчатых колес и длине подшипников скольжения, перекос колец подшипников качения. Деформация кручения валов вызывает неравномерность распределения нагрузки по длине шлицев в шлицевых соединениях, по длине венцов валов-шестерен, она может быть причиной потери точности ходовых винтов токарно-винторезных станков и причиной возникновения крутильных колебаний валов. Деформация валов мало влияет на работу ременных и цепных передач, поэтому валы таких передач на жесткость не проверяют. Жесткость коротких валов, например валов редукторов, обычно не контролируют, так как прогибы и углы закручивания таких валов невелики и жесткость их обеспечена. 13) Передача винт-гайка и ее расчет. Передача винт-гайка (винтовой механизм) предназначена для преобразования вращательного движения в поступательное. При этом как винт, так и гайка могут иметь либо одно из вышеназванных движений, либо оба движения одновременно. Например, в винтовом домкрате, изображенном на рис.1, винт совершает оба движения одновременно. Так, при вращении вертикального винта за рукоятку в неподвижной гайке винт получает поступательное перемещение и поднимает груз, опирающийся на чашку домкрата. F Достоинства передачи винт-гайка: - большой выигрыш в силе; - возможность получения медленного движения с высокой точностью перемещения; - компактность при высокой нагрузочной способности; - простота конструкции и изготовления. К недостаткам рассматриваемой передачи можно отнести большое трение в резьбе, вызывающее её повышенный износ, низкий К.П.Д. Основная причина выхода из строя гаек и винтов – износ, поэтому средний диаметр резьбы d2 определяется с учетом допускаемого удельного давления. 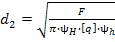 где F – осевая сила; ψН – коэффициент высоты гайки, принимаемый от 1,2 до 2,5 [q] – допускаемое удельное давление (табл.2.); ψh – коэффициент высоты резьбы, принимаемый: 0,5 – для прямоугольной резьбы; 0,65 – для трапециидальной; 0,75 – для упорной. Размеры прямоугольной резьбы определяются по формулам: высота профиля h = 0,1 * d2 наружный диаметр d = d2 + h внутренний диаметр d1 = d1 – h шаг резьбы p = 2 * h Для многозаходной резьбы определяется по формуле: p H = p ⋅n где n – число заходов. Винт проверяется на прочность при совместном действии осевой силы F и крутящего момента Т по эквивалентному напряжению: 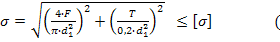 где [σp] = [σсж] – допускаемое напряжение растяжения-сжатия для материала винта Крутящий момент Т преодолевает момент трения в резьбе ТР и на опорах – Тm : T = T p + T m 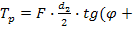 ψ) ψ)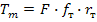 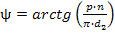 ,угол подъема резьбы; fт – коэффициент трения вала на торце; rт – радиус круга трения. ,угол подъема резьбы; fт – коэффициент трения вала на торце; rт – радиус круга трения.При необходимости проверка условия самоторможения может быть выполнена по условию самоторможения, при котором угол подъема резьбы должен быть меньше приведенного угла трения, иначе говоря ψ ≤ φ΄. В противном случае связанный с гайкой объект будет самопроизвольно перемещаться. Проверка винта на устойчивость может проводиться по объединенному условию прочности и устойчивости 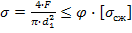 Гибкость стержня i = d1 / 4 – радиус инерции; μ – коэффициент приведения длины винта, зависящий от типа опорных закреплений: μ = 2 – при одной жесткой опоре; μ = 1 – при двух шарнирных опорах; опора считается шарнирной, если отношение ее длины lоп к среднему диаметру резьбы меньше 1,5; μ = 0,7 – одна опора жесткая, а другая шарнирная. При λ < 55 проверку на устойчивость не выполняют. При λ = 55…90 устойчивость винтов из сталей 40; 45; 50; Ст 5 можно проверить по формуле 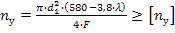 где [ny] = 2,5…4 – допускаемый коэффициент запаса устойчивости. При λ > 90 коэффициент запаса устойчивости определяется по формуле: 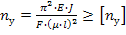 где Е – модуль упругости материала винта (для стали Е = 2,1 * 105 Мпа). J – приведенный момент инерции сечения винта, 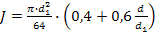 Расчет гайки винтового передаточного механизма начинают с определения ее высоты: H= ψh×d2 Число витков резьбы в гайке Z = H/p (54) Если Z > 10, то необходимо увеличить диаметр винта и повторить расчет. Наружный диаметр гайки определяется из условий прочности на растяжение: 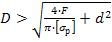 где [σp] – допускаемое напряжение растяжения материала гайки. Проверка на прочность элементов резьбы выполняется в следующих случаях. Если материалы винта и гайки одинаковы, то опасен срез витков винта, происходящий по цилиндрической поверхности d1, 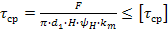 где km = 0,55…0,75 – коэффициент неравномерности распределения нагрузки между витками резьбы; [τср] – допускаемое напряжение среза материала винта. Опасным будет являться срез витков резьбы гайки в случае, если материал гайки менее прочен, чем материал винта. Этот срез может произойти по внутреннему диаметру резьбы (d4), или по наружному диаметру винта (d) в зависимости от типа резьбы: 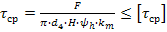 где [τср] – допускаемое напряжение среза материала гайки. Напряжение смятия в резьбе (расчетная формула является общей для винта и для гайки): 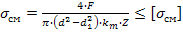 где [σсм] – допускаемое напряжение смятия материала винта или гайки. 14) Передачи. Передаточное отношение. Связь между крутящим моментом, угловой скоростью и мощностью. Передачей будем называть устройство, предназначенное для передачи энергии из одной точки пространства в другую, расположенную на некотором расстоянии от первой. В современном машиностроении в зависимости от вида передаваемой энергии применяют механические, пневматические, гидравлические и электрические передачи. Механическими передачами, или просто передачами, называют механизмы для передачи энергии от машины-двигателя к машине-орудию, как правило, с преобразованием скоростей, моментов, а иногда — с преобразованием видов (например, вращательное в поступательное) и законов движения.  Передаточное число – отношение угловой скорости ведущего вала к угловой скорости ведомого вала конкретной передачи. Передаточное число не может быть меньше единицы. Оно представляет собой абсолютную величину передаточного отношения: С 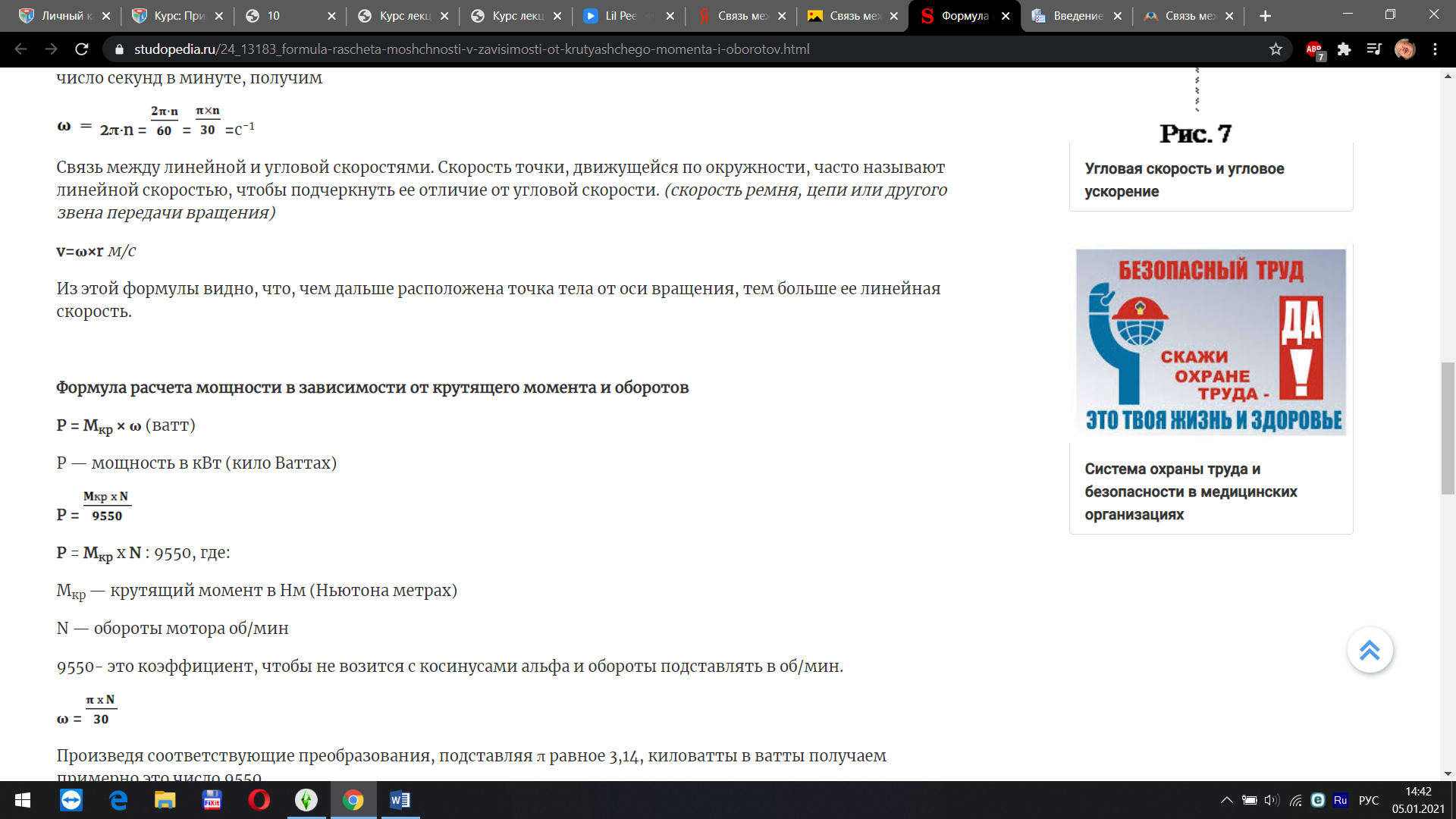 вязь между крутящим моментом, угловой скоростью и мощностью: вязь между крутящим моментом, угловой скоростью и мощностью: 15) Планетарные передачи. Достоинства и недостатки. Определение передаточного отношения.  Планетарными передачами называют механические передачи, имеющие колеса с перемещающимися геометрическими осями. Планетарными передачами называют механические передачи, имеющие колеса с перемещающимися геометрическими осями.Ведущим в планетарной передаче может быть либо центральное колесо Z1, либо водило H. Наиболее распространенная простейшая однорядная планетарная передача состоит из центрального колеса Z1 с наружными зубьями (солнечное колесо), неподвижного центрального колеса Z3 с внутренними зубьями и водила H, на котором закреплены оси планетарных колес или сателлитов Z2. Достоинства: 1. Малые габариты и масса (передача вписывается в размеры корончатого колеса). Это объясняется тем, что мощность передается по нескольким потокам, численно равным числу сателлитов, поэтому нагрузка на зубья в каждом зацеплении уменьшается в несколько раз. 2. Благодаря соосности ведущих и ведомых валов эти передачи удобны для компоновки машин. 3. Планетарные передачи работают с меньшим шумом, чем обычные зубчатые, что связано с меньшими размерами колес и замыканием сил в механизме. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются. 4. Малые нагрузки на опоры, что упрощает конструкцию опор и снижает потери в них. 5. Планетарный принцип передачи движения позволяет получить большие передаточные отношения при небольшом числе зубчатых колес и малых габаритах. Недостатки: 1. Повышенные требования к точности изготовления и монтажа передачи. 2. Снижение КПД передачи с ростом передаточного отношения. Передаточное отношение: При определении передаточного отношения используют метод остановки водила (метод Виллиса). По этому методу всей планетарной передаче мысленно сообщается дополнительное вращение с угловой скоростью водила ωH, но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны.  16) Подшипники качения. Виды разрушения. Расчет подшипников на долговечность и статическую грузоподъемность.  Достоинства: малые потери на трение и незначительный нагрев; малый расход смазки; высокая степень взаимозаменяемости; небольшие габариты в осевом направлении. Недостатки: чувствительность к ударным и вибрационным нагрузкам; большие габариты в радиальном направлении; малонадежны при высокой скорости. Виды разрушения и критерии работоспособности подшипников качения 1. Усталостное выкрашивание рабочих поверхностей тел и дорожек качения происходит вследствие действия на них циклических контактных напряжений. Усталостное выкрашивание является основным видом разрушения подшипников. 2. Пластические деформации в виде вмятин (лунок) на дорожках качения наблюдаются в невращающихся и тихоходных подшипниках (n 1 мин-1 ) при действии на них больших статических и ударных нагрузок. 3. Задиры рабочих поверхностей качения по причине недостаточной смазки или слишком малых зазоров из-за неправильного монтажа. 4. Абразивный износ вследствие плохой защиты подшипника от попадания пыли. 5. Разрушение сепараторов от действия центробежных сил и воздействия на сепаратор тел качения. Этот вид разрушения является основной причиной потери работоспособности быстроходных подшипников. 6. Раскалывание колец и тел качения из-за перекосов при монтаже или больших динамических нагрузок. Главные критерии работоспособности подшипников качения: усталостная контактная прочность и стойкость к пластическим деформациям. Поэтому различают следующие виды расчета подшипников качения: 1) на долговечность по динамической грузоподъемности – для предотвращения усталостного выкрашивания; 2) по статической грузоподъемности – для предотвращения пластической деформации.  17) Подшипники скольжения и их расчет. Подшипники, работающие по принципу трения скольжения, называются подшипниками скольжения. Достоинства подшипников скольжения: надежно работают в высокоскоростных приводах; способны воспринимать большие ударные и вибрационные нагрузки вследствие демпфирующего действия масляного слоя; обеспечивают высокую точность установки вала; работают бесшумно; имеют малые габариты в радиальном направлении; разъемные подшипники допускают установку их на шейки коленчатых валов; возможность использования при работе в агрессивной среде. Недостатки подшипников скольжения: в процессе работы необходим постоянный надзор из-за высоких требований к смазке и опасности перегрева; большие габариты в осевом направлении; большой расход смазочного материала; необходимость применения дорогостоящих и дефицитных антифрикционных материалов для вкладышей.  18) Проверка тела червяка на прочность и жесткость. На примере: Расстояние между серединами опор вала червяка при приближенном расчете можно принимать равным: L = 0.95×d2 = 0.95×200 = 190 (мм) Правильность зацепления червячной пары может быть обеспечена лишь при достаточной жесткости червяка. Средняя допускаемая стрела прогиба [f] червяка может быть принята:  Стрела прогиба червяка, вал которого опирается на два радиально-упорных подшипника определяется по формуле:  f= Здесь E= L – расстояние между серединами опор; Jпр – приведенный момент инерции сечения червяка, определяемый по эмпирической формуле:  Найдем реальную стрелу прогиба: 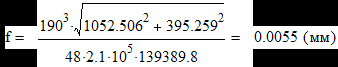 f < [f], следовательно, условие жесткости выполняется. 20) Расчет зубьев цилиндрических эвольвентных передач на изгиб. 1.Напряжение изгиба в опасном сечении 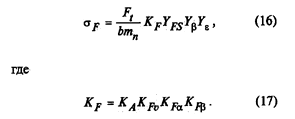 2. Допускаемое напряжение изгиба на переходной поверхности зуба, не вызывающее усталостного разрушения материала: 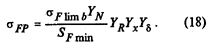 3. Допускаемое напряжение изгиба в опасном сечении, не вызывающее остаточных деформаций, хрупкого излома или первичных трещин: 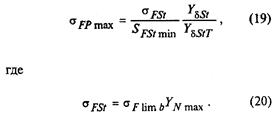 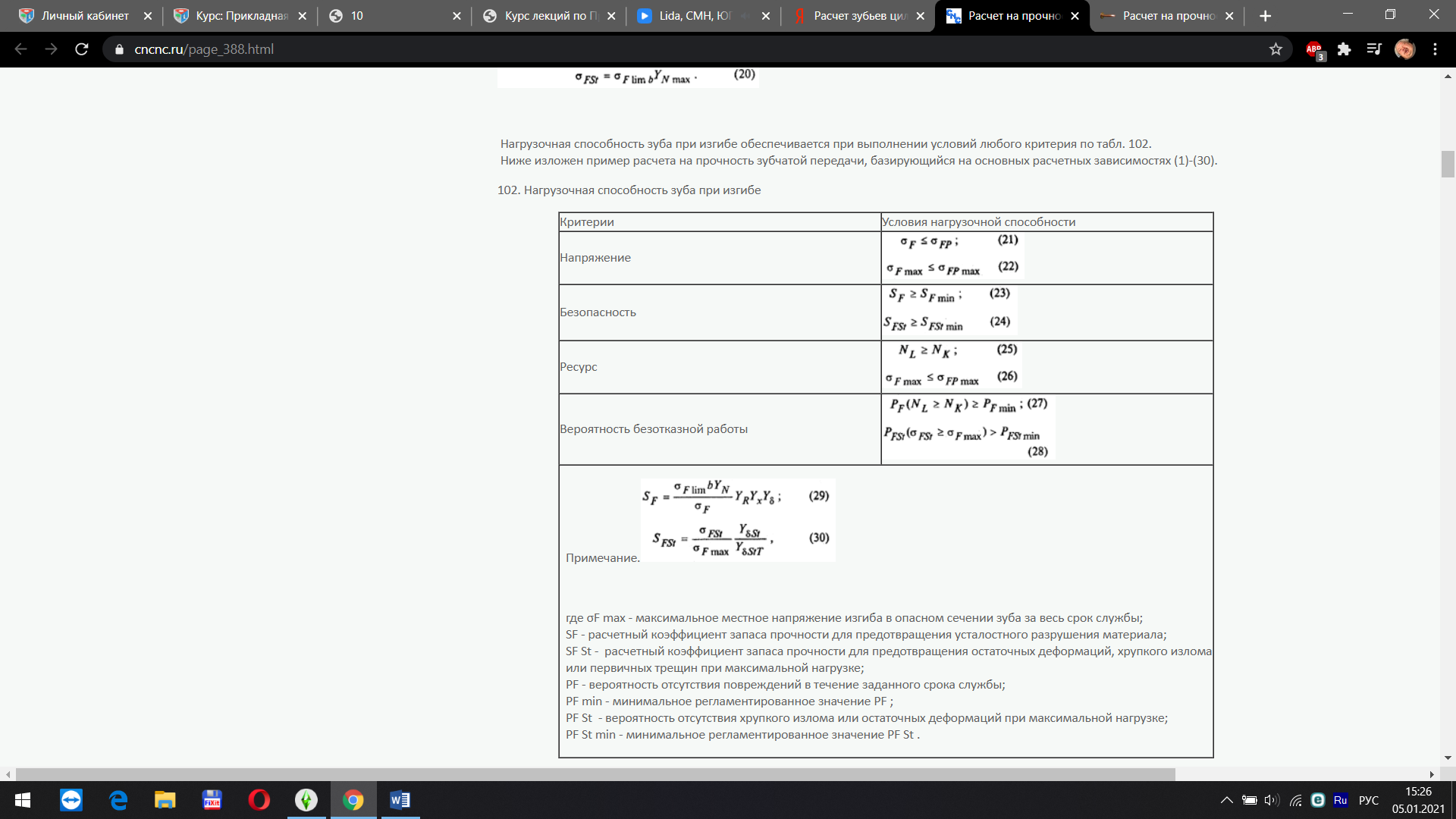 21) Расчет на прочность стержня винта (болта) при различных случаях нагружения. 1. Стержень винта нагружен только внешней растягивающей силой F. Примером служит резьбовой участок грузового болта для подвешивания груза. Опасным является сечение, ослабленное резьбой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d1 резьбы. Условие прочности по напряжениям растяжения в стержне. 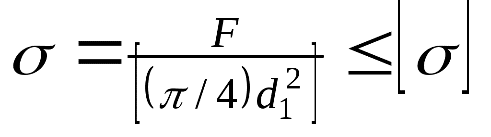 2. Болт затянут, внешняя нагрузка отсутствует. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин. В этом случае стержень болта растягивается осевой силой Fзат, возникающей от затяжки болта, и закручивается моментом сил трения в резьбе Тр, т.е. работает на кручение. Прочность болта определяют по эквивалентному напряжению Для стандартных метрических резьб расчеты показывают, что σэкв  1,3σ. Это позволяет производить расчет прочности болтов по упрощенной формуле 1,3σ. Это позволяет производить расчет прочности болтов по упрощенной формуле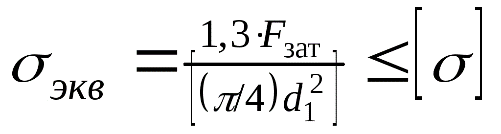 3. Болтовое соединение нагружено силами, сдвигающими детали в стыке. Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах: первый, болт поставлен с зазором; второй – болт поставлен без зазора. Начнем рассмотрение с варианта, когда болт поставлен с зазором. Внешняя нагрузка уравновешивается силами трения в стыке, которые образуются от затяжки болта. Без затяжки болтов детали могут сдвигаться на величину зазора, что недопустимо. Рассматривая равновесие детали 2, получаем условие отсутствия сдвига деталей F ≤i* Fтр=i*Fзат f, или Fзат=KF/(if), где i – число плоскостей сдвига деталей (на рисунке i = 2); f – коэффициент трения в стыке; ( f = 0,15…0,20); K – коэффициент запаса (K = 1,3…1,5 при статической нагрузке, K = 1,8…2 при переменной нагрузке). Болт поставлен без зазора.  Расчет на смятие производится по условным напряжениям из-за сложности установить точный закон распределения напряжений по цилиндрической поверхности деталей. При этом для средней детали (и при соединении только двух деталей)/ 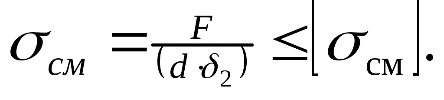 Д 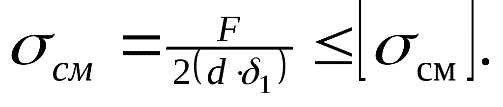 ля крайних деталей ля крайних деталей4. Болт затянут, внешняя нагрузка раскрывает стык деталей. 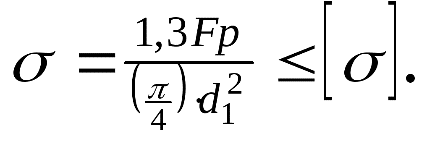 А) Прочность болта при статической нагрузке: А) Прочность болта при статической нагрузке:Б) Прочность болта при переменных нагрузках. 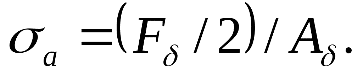 22) Расчет прочности зубьев цилиндрических эвольвентных закрытых передач внешнего зацепления по контактным напряжениям.   , ,  - радиусы кривизны ρ1 и ρ2 эвольвент зубьев в точке контакта. - радиусы кривизны ρ1 и ρ2 эвольвент зубьев в точке контакта.Отсюда приведенный радиус кривизны:  где  ( +) для наружного зацепления; ( _) для внутреннего зацепления. ( +) для наружного зацепления; ( _) для внутреннего зацепления. Это условие прочности по контактным напряжениям. Параметр u=z2/z1 – отношение большего числа зубьев к меньшему числу. Отличается от передаточного отношения i , которое равно отношению угловых скоростей ведущего колеса к ведомому. |
