1. Задачи,приводящие к понятию производной а о скорости движения материальной точки

• Название: 1. Задачи,приводящие к понятию производной а о скорости движения материальной точки
• Анкор: FIZIKA1.docx
• Дата: 29.04.2018
• Размер: 1.34 Mb.
• Имя файла: FIZIKA1.docx
• Тип: Документы; #18650
• страница: 2 из 10

7.Случайные события. Классическое и статистическое определения вероятности случайного события. Виды случайных событий

Случайным называется событие ,наступление которого нельзя достоверно предвидеть. В одних и тех же доступных наблюдению условиях оно может произойти , может и не произойти.

Относительной частотой случайного события в данной серии испытаний или просто частотой случайного события А называют отношение :



Виды случайных событий:

1.Событие , которое при данном испытании произойдет обязательно , называется достоверным , его вероятность равна 1( например, достоверным является событие ,состоящее в извлечении наугад упаковки аспирина из ящика, в котором находится только упаковка аспирина)

2.Событие, которое при данном испытании не может произойти , называется невозможным ,его вероятность равна нулю( например , невозможным является событие , состоящее в извлечении наугад упаковки аспирина из ящика, в котором находятся только упаковки анальгина)

3.События называются несовместимыми, если появление любого из них в результате испытания исключает появления других.( например ,если событие А1состоит в выпадении цифры 1 при однократном бросании игрального кубика, событие А2- в выпадении цифры 2 и т.д., то события являются несовместимыми, поскольку осуществление любого из них исключает наступление остальных событий в этом испытании)

4.События называются совместными ,если появление любого из них в результате испытания не исключает появления остальных.(например ,если событие А1 состоит в выпадении цифры 1 при однократном бросании игрального кубика,а событие А2- в выпадении нечетного числа очков, то эти два события являются совместными ,поскольку 1 является нечетным числом)

5.Событие В называется благоприятствующим для события А, если при наступлении события В обязательно наступает событие А

6.Событие А и В называется независимыми ,если вероятность наступления каждого из них не зависит от того, наступило ли при этом другое событие.(например ,при одновременном подбрасывании двух монет случайное событие А ,состоящее в выпадении герба у одной монеты , и событии В , состоящее в выпадении герба у другой монеты , являются независимыми событиями)

7.Событие В называется зависимым от события А,если вероятность наступления события В зависит от того, произошло ли событие А

8.Если два события единственно возможны и несовместимы , то их называют противоположными и обозначают А и Ā: Р(А)+Р(Ā)=1

9.Система событий А1,А2,…,Аn называется полной ,если в результате испытания обязательно наступает только одно из этих событий. Сумма вероятностей событий , образующих ролнкю систему , равна единице: Р(А1)+Р(А2)+…..+Р(Аn)=1

Существуют классическое и статистическое определение вероятности события. Их основное отличие друг от друга состоит в том, что классическое определение вероятности основывается исключительно на умозаключениях и не предполагает проведения какого бы то ни было эксперимента, в то время как статистическое определение вероятностей, наоборот, не связано ни с какими рассуждениями, а основывается только лишь на проводимых многочисленных испытаниях.

Статистическое определение вероятности

Вероятностью случайного события назовем предел ,к которому стремится частота события при неограниченном увеличении числа испытаний

Это статистическое определение вероятности
. Классическое определение.

Если при испытаниях нет каких-либо причин ,вследствие которых одно случайное событие появлялось бы чаще других ,то можно определить вероятность исходя из теоретических соображений :
Вероятность события равняется отношению числа благоприятствующих исходов к общему числу возможных исходов

 

где  — вероятность события ,  — число благоприятствующих событию исходов,  — общее число возможных исходов.

Это классическое определение вероятности

8.Основные теоремы теории вероятностей.Повторные независимые испытания. Формула Бернулли.Формула Пуассона.

Теорема сложения вероятностей.Вероятность наступления случайного события А или несовместимого с ним события В равна сумме вероятностей этих событий :Р(А илиВ)=Р(А)+Р(В)

Теорема умножения вероятностей для независимых событий . Вероятность наступления двух независимых случайных событий А и В \равна произведению вероятностей этих событий: Р(А илиВ)=Р(А)·Р(В)

Теорема умножения вероятностей для зависимых событий .Вероятность наступления случайного события А и зависящего от него события В равна произведению вероятностей события А на условную вероятность события В: Р(А или В)=Р(А)·Р(В/А)

Повторными независимыми испытаниями называют испытания ,удовлетворяющие следующим условиям:

1)количество испытаний конечно

2)вероятность осуществления случайного события А в каждом из испытаний постоянна:

P(A)=p=const

Такая схема испытаний называется схемой Бернулли

Вероятность того ,что в серии из n независимых испытаний ,в каждом из которых вероятность наступлдения случайного события А равна p ,это событие произойдет m раз дается формулой Бернулли :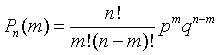



Q=1-P –ВЕРОЯТНОСТЬ НАСТУПЛЕНИЯ СОБЫТИЯ В КАЖДОМ ИЗ ИСПЫТАНИЙ


Если объем n независимых повторных испытаний велик, то использование формулы Бернулли сопряжено с вычислительными трудностями . Однако ,если n не меньше нескольких десятков, а вероятность наступления случайного события в каждом из испытаний мала (р<<1), причем 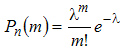не превышает 10, , то для получения приближенного значения соответствующей вероятности пользуются формулой Пуассона :

P_n(m),  или ( )
 

(8) также называют«законом редких испытаний».

Эта формула является приближенной, однако получаемые с ее помощью результаты тем ближе к точным, чем больше количество испытанийn.
9.Дискретные случайные величины.Закон распределения дискретной случайной величины.Основные числовые характеристики дискретнойслучайной величины и ее свойства.

Случайной величиной называют такую величину ,которая в результате эксперимента принимает какое-либо одно значение из множества ее возможных значений ,причем до эксперимента невозможно предсказать какое именно .

Случайная величина называется дискретной, если совокупность всех ее возможных значений представляет собой конечное или бесконечное, но обязательно счетное множество значений, т.е такое множество, все элементы которого могут быть пронумерованы и выписаны соответствующей последовательности.

X	x1	x2	x3	..	xn
P	P1	p2	p3	..	pn

: Закон распределения дискетной случайной величины- это соответствие между всеми возможными значениями этой случайной величины и соответствующими им вероятностями.

Закон распределения дискретной случайной величины часто задают в виде двухстрочной таблицы, в первой строке которой перечислены все возможные значения этой величины (в порядке возрастания), а во второй -соответствующие этим значениям вероятности .

Так как все возможные значения дискретной случайной величины представляют полную систему, то сумма вероятностей равна единице (условие нормировки):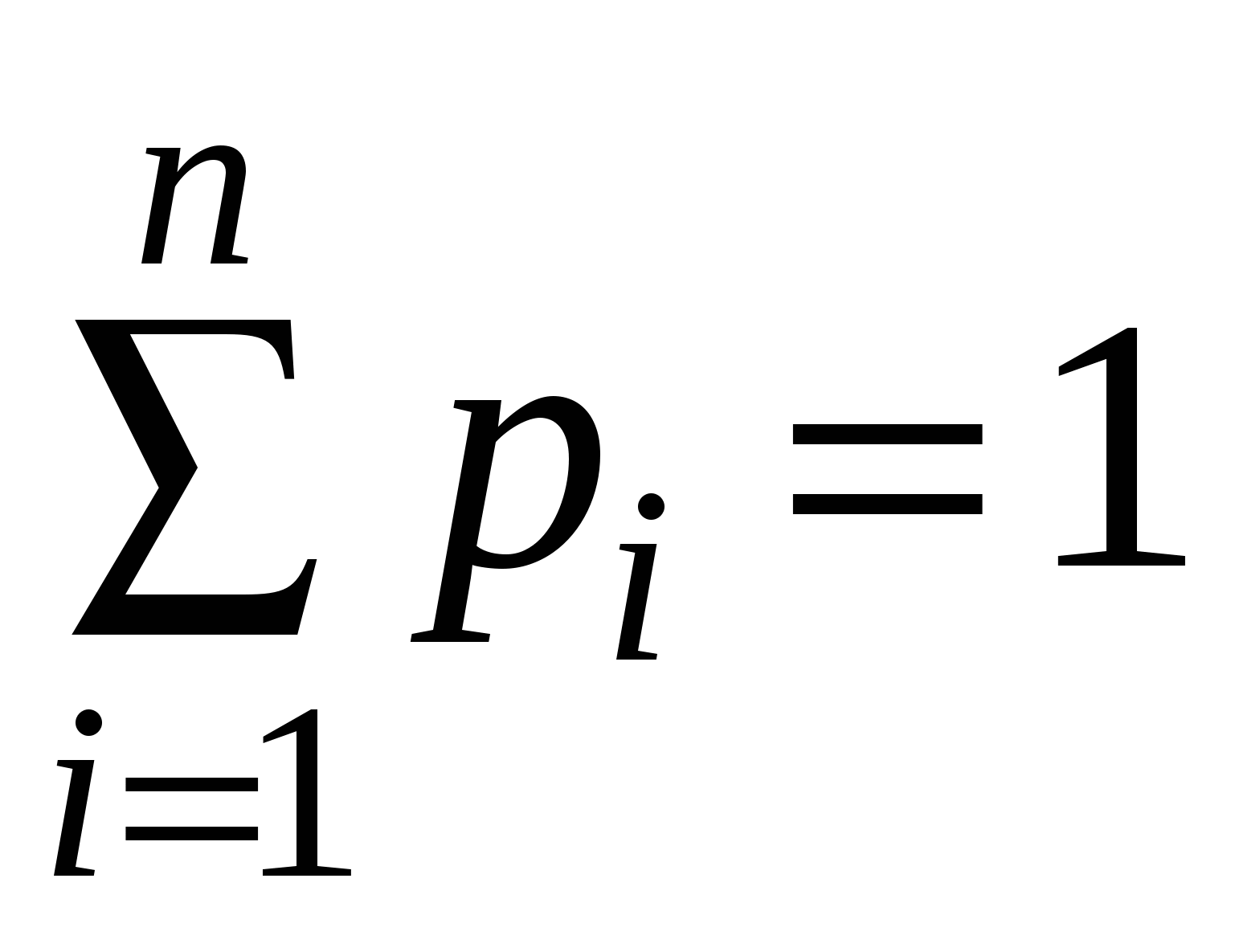

, 

Для описания определенных особенностей дискретной случайной величины используют ее основные числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение:

Математическим ожиданием дискретной случайной величины х называется сумма произведений каждого из всех ее возможных значений на соответствующие вероятности.

M(x)=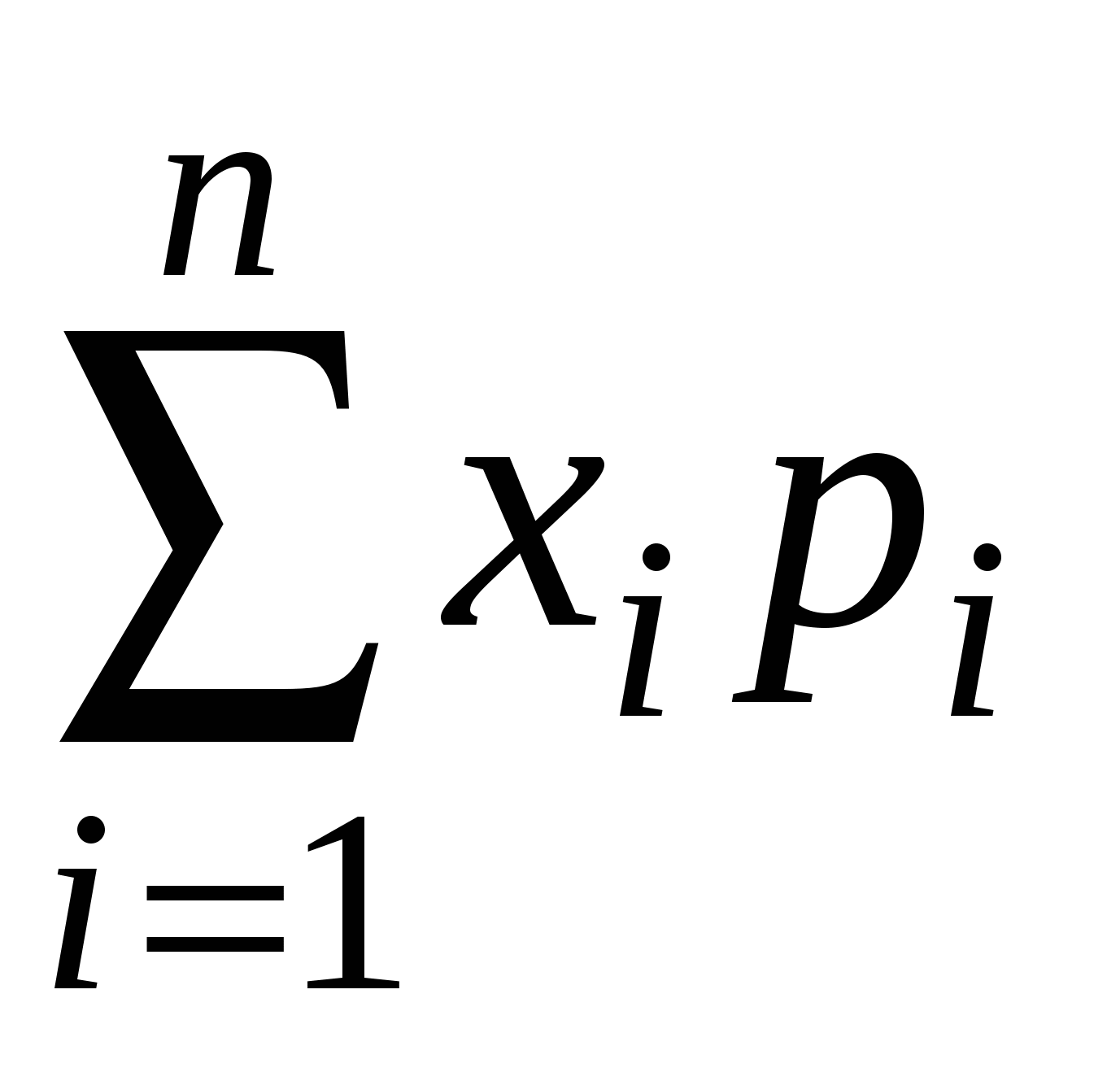

Св-ва математического ожидания: 1) Математич. ожидание постоянной величины равно этой постоянной величине М(С)=С; 2) Математич. ожидание произведения постоянного множителя на дискретную случайную величину равно произведению этого постоянного множителя на математическое ожидание данной случайной величины: M(kX)=kM(X); 3) Математич. ожидание суммы двух случайных величин равно сумме математических ожиданий этих величин: M(X+Y)=M(X)+M(Y);

Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания.

D(X) = M[X – M(X)]². (добавить)

Св-ва дисперсии: 1) Дисперсия постоянной величины равна нулю: D(C)=0; 2)Дисперсией любой величины есть число неотрицательное: D(X)≥0; 3) Дисперсия произведения постоянного множителя 3) Дисперсия произведения постоянного множителя k на дискретную случайную величину равна произведению квадрата этого постоянного множителя на дисперсию данной случайной величины: D(kX)=k²*D(X).

Средним квадратическим отклонением дискретной случайной величины называется квадратный корень из ее дисперсии : σ(х)= √D(X)

10.Непрерывные случайные величины.Функция распределениянепрерывной случайной величины и ее свойства.

Случайная величина называется непрерывной, если множество ее возможных значений представляет собой некоторый конечный или бесконечный промежуток числовой оси. Например: температура больного в фиксированное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента и т.д.

Одним из возможных способов задания непрерывной случайной величины является использование с этой целью соотв. функции распределения. Функция F(x), равная вероятности того, что случайная величина Х в результате испытания примет значение , меньше х, называется функцией распределения данной случайной величины :F(x)=P(X<x)
Свойства функции распределения: 1) Функция распределения удовлетворяет неравенству: 0≤F(x)≤1 ; 2) Функция распределения является неубывающей функцией, т.е. из х_2>х₁ следует F(x2)≥F(x1). 3)Функция распределения стремится к 0 при неограниченном убывании еаргумента и стремится к 1 при его неограниченном возрастании.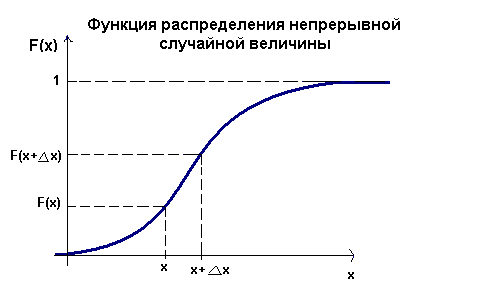

График функции распределения

11.Плотность распределения вероятностей непрерывной случайной величины и ее свойства. Основные числовые характеристики непрерывной случайной величины.

Плотностью распределения вероятностей (плотностью вероятности) f(x) непрерывной случайной величины Х называется производная функции распределения F(x) этой величины: f(x)=F’(x)

Свойства плотности распределения вероятностей: 1) Плотность вероятности является неотрицательной функцией: f(x)≥0; 2) Вероятность того, что в результате испытания непрерывная случайная величина примет какие либо значения из интервала (a,b) равна: 3) Определенный интеграл в пределах от –бесконечности до + бесконечности от плотности вероятности непрерывной случайной величины равен единице : 4) Определенный интеграл в пределах от минус бесконечности до х от плотности вероятности непрерывной случайной величины равен функции распределения этой величины: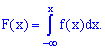

Под основными числовыми характеристиками непрерывной случайной величины понимают, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Математическое ожидание непрерывной случайной величины:

Дисперсия непрерывной случайной величины D(X) = M[X – M(X)]². (добавить)

Среднее квадратическое отклонение: σ(х)= √D(X)

12. Нормальный закон распределения. Вероятность попадения нормально распределенной случайнойвеличиныв заданный интервал.Правило трех сигм.

Из всех видов распределения непрерывных случайных величин наиболее часто используют нормальное распределение, которое задается законом Гаусса. Так, если мы имеем сумму большого числа независимых величин, подчиненных каким угодно законам распределения, то при некоторых общих условиях она будет приближенно подчиняться нормальному закону. Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность вероятности имеет вид : 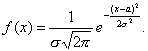(увеличить,дописать), где М-математическое ожидание, σ в квадрате – дисперсия, σ-среднее квадратическое отклонение этой величины.это кривая Гаусса: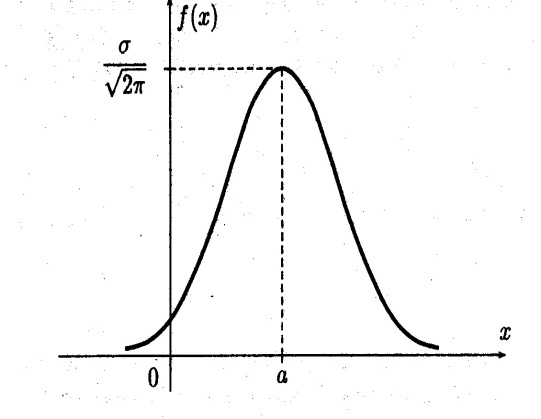



Подставив выражение 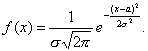для плотности вероятности нормально распределенной случайной величины в выражение , получим вероятность того, что в результате испытания нормально распределенная случайная величина

примет значение из заданного интервала : P(a<X<b)=____________________

Правило трех сигм: отклонения значений нормального распределения случайной величины от ее математического ожидания по абсолютной величине практически не превышает ее утроенного среднего квадратического отклонения.