1. Задачи,приводящие к понятию производной а о скорости движения материальной точки

• Название: 1. Задачи,приводящие к понятию производной а о скорости движения материальной точки
• Анкор: FIZIKA1.docx
• Дата: 29.04.2018
• Размер: 1.34 Mb.
• Имя файла: FIZIKA1.docx
• Тип: Документы; #18650
• страница: 3 из 10

13. Статистическая совокупность .Генеральная и выборочная статистические совокупности. Статистический дискретный ряд распределения .Полигоны частот и относительных частот.

Статистическая совокупность- это множество объектов, характеризуемых некоторым качественным или количественным признаком .

Генеральная статистическая совокупность- статистическая совокупность ,состоящая из всех объектов ,которые подлежат обследованию.Число объектов генеральной совокупности называют ее объемом и обозначают N

Статистическая совокупность, состоящая из некоторого количества объектов, случайным образом отобранных из соответствующей генеральной совокупности, называется выборочной статистической совокупностью(выборкой)Число объектов выборки называют ее объемом и обозначают n

Статистический ряд

 Пусть требуется изучить распределение значений признака Х у объектов некоторой генеральной совокупности.          Для этого из генеральной совокупности извлекают некоторую выборку объемом n.          Пусть в полученной выборочной совокупности  наименьшее значение признака x1 встречается m1 раз, следующее по величине значение x2-m2   раз,…….,  xk- mk раз.          Наблюдаемые значения признака называются вариантами, а числа  m1,m2,m3,…..,mk- их частотами.                                            Очевидно, что сумма всех частот равна объему выборки:    

  m1 + m2 +….mk =________________________,       Результаты наблюдений представим в виде таблицы, в первой строке которой в порядке возрастания перечислены все варианты    , во второй – соответствующие им частоты:  

       

Такая таблица называется статистическим дискретным рядом распределения.

 Для графического изображения такого ряда на координатной плоскости откладывают точки (xi; mi) и соединяют их отрезками прямых Полученная ломаная линия, являющаяся графическим изображением дискретного статистического ряда распределения, называется полигоном частот.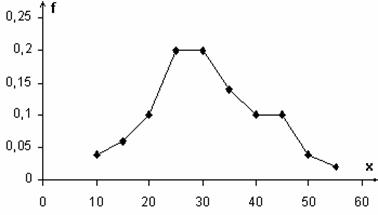       



Наряду с частотами mi часто применяются относительные частоты  Pi=,_________ сумма которых равна единице:

_______________________

14.Статистический интервальный ряд распределения.Гистограммы частоти относительных частот.

Использование дискретного ряда распределения на практике удобно лишь в случае ограниченного количества различающихся между собой вариант в выборке. Если же количество таких вариант значительно больше, то результаты представляют в виде статистического интервального ряда распределений.    Для построения  такого ряда область наблюдаемых значений изучаемого признака разбивается на небольшое количество равных по величине интервалов и фиксируется количество значений признака в каждом интервале (частота интервала).      

Составим таблицу, в первой строке которой перечислены все частичные интервалы, во второй – соответствующие им частоты 


  Такая таблица называется статистическим интервальным рядом распределения, а его графическим изображением является  гистограмма частот
 Гистограмма  частот – это фигура, состоящая из прямоугольников, основаниями которых

служат частичные интервалы длиной Δx, а высотами  -отношения __________ (плотности частот).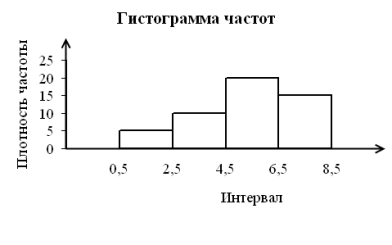    

На практике часто во второй строке статистического интервального ряда распределения  вместо частот mi указывают относительные частоты pi=___

 Тогда графическим изображением такого ряда распределения является гистограмма относительных частот, при построении которой по оси ординат откладывают плотность относительной частоты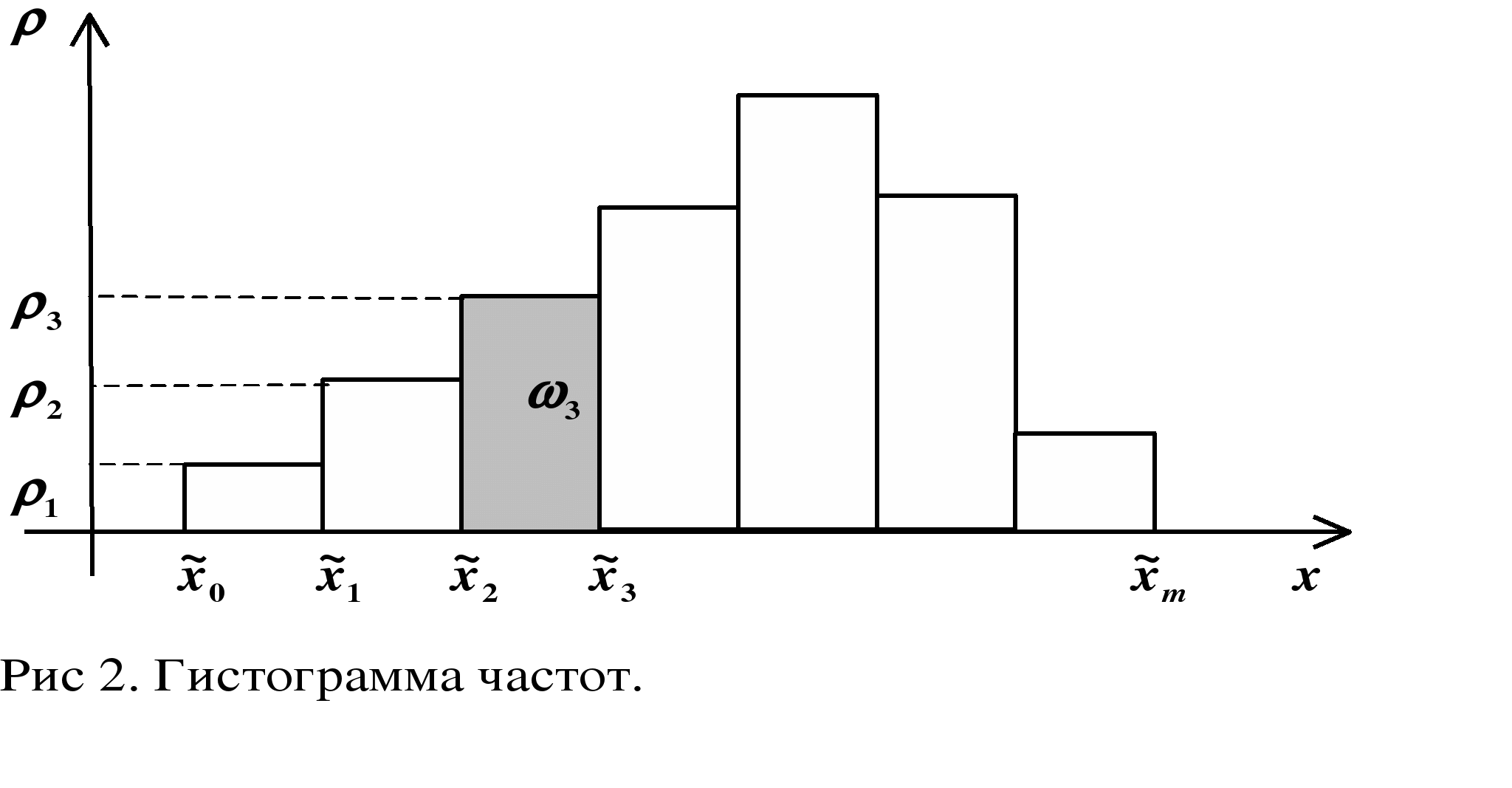 




15.Выборочные характеристики распределения.Точечные оценки основныхчисловых характеристик генеральной совокупности

Под выборочными характеристиками распределения понимают основные числовые характеристики выборочной статистической совокупности: среднюю выборочную, выборочную дисперсию и выборочное среднее квадратичесоке отклонение.

Оценка характеристики распределения называется точечной, если она определяется одним числом, которому приближенно равна оцениваемая характеристика.

Генеральной средней Х дискретной генеральной совокупности называется среднее арифметическое всех значений изучаемого признака Х в генеральной совокупности

_____________________,где N-объем совокупности

Генеральная средняя равна математическрму ожиданию случайной величины___________________

Наилучшей оценкой генеральной средней  является средняя выборочная, определяемая как среднее арифметическое всех значений изучаемого признака в выборке:       
_____________________________,где mi - частота встречаемости значения  в выборке,k - количество вариант, n - объем выборки.
 

Математическим выражением того факта, что средняя выборочная представляет собой наилучшую оценку генеральной средней, является приближенное равенство:

_________

Генеральной дисперсией σ в квадрате называется среднее арифметическое квадратнов отклонений всех значений изучаемого признака х в генеральной совокупности от генеральной средней

 

Наилучшей оценкой генеральной дисперсии является так называемая исправленная выборочная дисперсия , определяемая по формуле:

Генеральным средним квадратическим отклонением  называется квадратный корень из генеральной дисперсии

 Наилучшей оценкой генерального среднего квадратического отклонения  является исправленное выборочное среднее квадратическое отклонение , определяемое по формуле

16.Интервалтьные оценки числовых характеристик генеральной совокупности.Доверительный интервал,доверительная вероятность. Распределение Стьюдента.

Оценка характеристики распределения называется интервальной, если она определяется двумя числами- границами интервала, содержащего оцениваемую характеристику.

 В математической статистике используют так называемые доверительные интервалы, соответствующие заданной доверительной вероятности.  

 Доверительной вероятностью (надежностью) оценки числовой характеристики с помощью доверительного интервала называется вероятность того, что эта характеристика находится в данном интервале. Чем шире доверительный интервал, тем выше соответствующая доверительная вероятность, и наоборот: чем большую доверительную вероятность мы хотим обеспечить, тем большим окажется соответствующий доверительный интервал.       

 В фармации, медицине и биологии доверительную вероятность принимают равной 0,95 или 0,99.  

    Рассмотрим метод нахождения доверительного интервала для заданной доверительной вероятности при оценке генеральной средней по результатам выборочных наблюдений. Предполагается, что изучаемый признак в генеральной совокупности распределен по нормальному закону. Метод основан на использовании распределения Стьюдента  для случайной величины:

_______________________,где _____________________ -исправленное квадратическое отклонение средней выборочной

Полуширина доверительного интервала для интервальной оценки генеральной средней при заданной доверительной вероятности γ находится по формуле:

_____________________

,где tγ(f)-коэф Стьюдента для доверительной вероятности γ и числа степеней свободы f=n-1 Тогда интервальная оценка генеральной средней представляется доверительным интервалом:

17. Основные понятия и определения колебательных процессов. Механические колебания. Гармонические колебания. Незатухающие колебания.
Колебаниями называются любые процессы, более или менее точно повторяющиеся через равные промежутки времени, называемые периодом колебания. В зависимости от физической природы процесса различают колебания механические, электрические и т.д. Но все колебания подчиняются общим закономерностям. При смещении тела из устойчивого положения равновесия возникает внутренняя возвращающая сила F_воз, пропорциональная смещению S тела и противодействующая ему:

F_воз= – ks, где k – коэффициент пропорциональности.

Такая сила называется упругой силой.
Для колебаний используют следующие характеристики:

• 
  период колебанийТ, равный времени, в течение которого совершается одно полное колебание;
  
• 
  частота колебанийν, равная числу колебаний, совершаемых за одну секунду (ν = 1/Т);
  
• 
  амплитуда колебанийА, равная максимальному смещению от положения равновесия.
  

Наиболее простой формой колебаний являются гармонические колебания. Это колебания, которые уже установились и происходят без потерь на трение, т.е. с неизменной амплитудой (незатухающие). Важнейшим признаком гармонических колебаний является изменение смещения во времени по закону синуса или косинуса.

, где

х – смещениетела в момент времени t;

А – амплитудаколебаний, равная максимальному смещению;

ω– круговая частотаколебаний (число колебаний, совершаемых за 2πсекунд), связанная с частотой колебаний соотношением.

Графиком гармонического колебания является синусоида.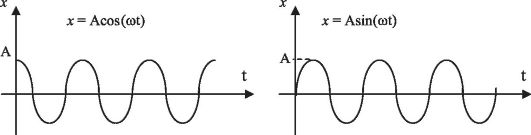


Свободныеилисобственные – это колебания, которые происходят в системе, предоставленной самой себе, после того как она была выведена из положения равновесия.

Примером могут служить колебания шарика, подвешенного на нити. Для того чтобы вызвать колебания, нужно либо толкнуть шарик, либо, отведя в сторону, отпустить его.

Свободные колебания могут быть незатухающими только при отсутствии силы трения. В противном случае первоначальный запас энергии будет расходоваться на ее преодоление, и размах колебаний будет уменьшаться.

18. Затухающие колебания. Вынужденные колебания. Резонанс. Автоколебания.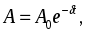
Колебания, энергия которых уменьшается с течением времени, называются затухающими. Убыль энергии связана с действием сил трения в колеблющейся системе и других сил сопротивления. Если для гармонических периодических колебаний амплитуда постоянна, то амплитуда затухающих колебаний изменяется по закону

где А₀ - начальная амплитуда колебаний в момент времени t = 0, δ-коэффициент затухания, который зависит от сил трения и массы колеблющегося тела. При не слишком больших скоростях силу трения можно считать пропорциональной скорости колебаний v, т.е.F_тр = - rv, где r - коэффициент трения, и в этом случае
где m -масса тела

Значения физических величин, характеризующих затухающие колебания, никогда не повторяются, т.е. затухающие колебания являются непериодическими.

График затухающих колебаний имеет вид:


Вынужденные колебания. Автоколебания. Резонанс

Незатухающие колебания системы, вызываемые действием на нее внешней периодической силы F(t), называются вынужденными.

Сила F(t) называется возмущающей или вынуждающей силой.

Если F(t) меняется по гармоническому закону: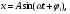
то соответствующие вынужденные колебания могут быть также гармоническими с частотой вынуждающей силы:

где А - амплитуда вынужденных колебаний физической величины, φ₁ - разность фаз между вынужденными колебаниями величины хи силы F(t).

Амплитуда установившихся вынужденных колебаний дается формулой


где F₀ - амплитуда возмущающей силы, m- масса колеблющейся системы, ω₀- циклическая частота свободных незатухающих колебаний системы, ω- циклическая частота внешней силы, δ-коэффициент затухания.

Разберем различные случаи:

1) При ω = 0 А=A₀ = F₀ /mω₀² . При этом колебания не совершаются и отклонение системы из положения равновесия называется статическим отклонением.

2) δ = 0 (отсутствует затухание). Амплитуда вынужденных колебаний А растет с увеличением ω, а при ω = ω₀ А→ ∞. С дальнейшим ростом ωамплитуда А уменьшается.

3) δ ≠ 0 - затухание существует. Амплитуда вынужденных колебаний А максимальна при



ω = ω_рез = ω₀
Явление возрастания амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы к значению ω_рез называется резонансом.

Величина ω_рез называется резонансной циклической частотой, а кривые зависимости А отω (рис. 5) – резонансными кривыми. Форма резонансных кривых зависит от величины коэффициента затухания δ .

Автоколебания– незатухающие колебания, поддерживаемые внешним источником энергии, поступление которой регулируется самой колебательной системой.

Система, совершающая незатухающие колебания за счёт действия источника энергии, не обладающего колебательными свойствами, называется автоколебательной системой.

Любая автоколебательная система состоит из 4 частей:

1. Колебательная система;

2. Источник энергии;

3. Клапан;

4. Обратная связь.


Если за время воздействия источника энергии на колебательную систему источник энергии производит над системой положительную (отрицательную) работу и передает ей (отнимает от нее) некоторый запас энергии, то обратная связь называется положительной ( отрицательной ).Положительная обратная связь используется для возбуждения автоколебаний. В случае отрицательной обратной связи усиливается затухание и автоколебания подавляются
19. Механические (упругие) волны. Основные характеристики волн. Уравнение плоской волны. Поток энергии и интенсивность волны. Вектор Умова.
Любое возмущение состояния вещества или поля, распространяющиеся в пространстве с течением времени называются волнами.

Механической волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию. Различают два основных вида механических волн: упругие волны (распространение упругих деформаций) и волны на поверхности жидкости. Упругие волны возникают благодаря связям, существующим между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с конечной скоростью.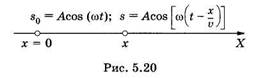

Пусть волна распространяется вдоль оси ОХ без затухания так, что амплитуды колебаний всех точек одинаковы и равны. Пусть в источнике волн изменения колеблющейся системы происходят по закону:



До точки с некоторой произвольной координатой х возмущение от начала координат дойдет через время τ(знак с формулы), поэтому колебания этой точки запаздывают



Т.к время и скорость связаны зависимостью ,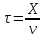

,то получаем :

Это и есть уравнение плоской волны
Основные характеристики волн:

• 
  Частота волны – частота колебаний точек среды, в которой распространяется волна.
  
• 
  Фронт волны –геометрическое место точек, до которых к данному моменту дошло колебание (возмущение среды).
  
• 
  Скорость волны (v) – скорость перемещения её фронта.
  
• 
  Длина волны – расстояние, на которое перемещается её фронт за время, равное периоду колебаний частиц среды.