1. Задачи,приводящие к понятию производной а о скорости движения материальной точки
 Скачать 1.34 Mb. Скачать 1.34 Mb.
|
        1.Задачи ,приводящие к понятию производной: а)о скорости движения материальной точки б) об угле наклона касательной к графику функции А.Пусть некоторая материальная точка совершает прямолинейное движение. В момент времени t1 точка находится в положении М1. В момент времени t2 в положении М2. Обозначим промежуток М1,М2 через ΔS ; t2-t1=Δt . Величина ΔS/Δt называется средней скоростью движения. Чтобы найти мгновенную скорость точки в положении М1 необходимо Δt устремить к нулю. Математически это значит, что: VM1= 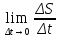 , таким образом , для нахождения мгновенной скорости материальной точки необходимо вычислить предел отношения приращения функции ΔS к приращению аргумента Δt при условии ,что Δt →0. , таким образом , для нахождения мгновенной скорости материальной точки необходимо вычислить предел отношения приращения функции ΔS к приращению аргумента Δt при условии ,что Δt →0.Б.График: 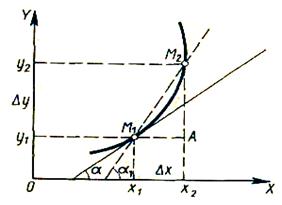 Рассмотрим график некоторой функции y=f(x). В точке М1 проведем касательную к графику функции. На графике выберем производную М2 и проведем секущую . Она наклонена к оси ОХ под углом α1. Рассмотрим ΔM1M2A: tgα1= 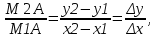 Если точку М1 фиксировать, а точку М2 приближать к М1 , то секущая М1М2 будет переходить в касательную к графику функции в точке М1 и можно записать: tgα= Если точку М1 фиксировать, а точку М2 приближать к М1 , то секущая М1М2 будет переходить в касательную к графику функции в точке М1 и можно записать: tgα=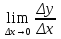 . Предел отношения приращения △у функции у=f(x) к приращению аргумента △x в заданной точке х0 при стремлении △х к нулю, называется производной функции в заданной точке. Обозначения производной: y’,f’(x), . Предел отношения приращения △у функции у=f(x) к приращению аргумента △x в заданной точке х0 при стремлении △х к нулю, называется производной функции в заданной точке. Обозначения производной: y’,f’(x),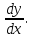 По определению y’= По определению y’=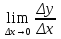 , где Δх=х2-х1-приращение аргумента, Δу=у2-у1-приращение функции. , где Δх=х2-х1-приращение аргумента, Δу=у2-у1-приращение функции. 2.Производная функции.Геометрический и механический смыслы производной.Производные основных элементарных функций.Производная сложной функции. Предел отношения приращения △у ФУНКЦИИ У=f(x) к приращению аргумента △x в заданной точке х0 при стремлении △х к нулю, называется производной функции в заданной точке . Обозначения производной : ______________________________ _______________________________________________ ,где Нахождения производной функции называется дифференцированием.Дифференциирование основных элементарных функций проводится по формулам и правилам : 1,(u+v+w) '=u '+v '+w ' 2. (u v)=u '+v '+w ' 3. Геометрический смысл производной. Величину тангенса угла наклона касательной ,проведенной к графику функции,в математике называют угловым коэффицентом касательной . Угловой коэффицент касательной ,проведенной к графику дифференцируемой функции в некоторой точке ,численно равен производной функции в данной точке Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + 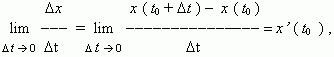 отсюда, v ( t0 ) = x’ ( t0 ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной.Аналогично, ускорение – это производная скорости повремени: a = v’ ( t ).  Производная сложной функции .Из элементарных функций образуются сложные функции .Например ,задана функция y=f(u),где u в свою очередб зависит от х , т.е u=φ(x). Тогда,при изменении х будут меняться u и y .В этом члучае заданная функция y=f(u) называется СЛОЖНОЙ и обозначается y=f{ φ(x)}.Величина u называется ПРОМЕЖУТОЧНОЙ ПЕРЕМЕННОЙ .тогда : y ' =y ' u * u ' x 3.Дифференциал функции.Аналитический и геометрический смысл дифференциала Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента) и обознвчается dy 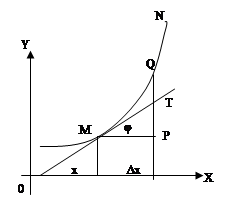 Дифференциал функции,в общем случае отличаясь от приращения функции ,представляет собой главную часть этого приращения ,линейную относительно приращения аргумента.В этом заключается аналитический смысл дифференциала Дифференциал функции является приращением ординаты касательной( АВ), которое соответствует приращению х (МВ) абсциссы. В этом заключается геометрический смысл дифференциала. Дифференциалом называют приращение аргумента,т.е dx=Δx 4.Первообразная функции. Неопределенный интеграл, его свойства. Таблица основных неопределенных интегралов. Функция F (x) называется первообразной для функции f (x) на интервале (a,b), если она дифференцируема на этом интервале и в каждой его точке F’(x)=f(x) Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как Функция f(x) называется подынтегральной функцией ,f(x)dx- подынтегральным выражением Если F(x)- какая-нибудь первообразная функции f(x),то где С - произвольная постоянная. Свойства неопр интеграла : . Дифференциал от неопределенного интеграла равен подынтегральному выражению Производная от неопределенного интеграла равна подынтегральной функции Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций  5. Определенный интеграл. Формула Ньютона-Лейбница. Свойства определенного интеграла. Геометрический смысл определенного интеграла. Определенный интеграл. Разность F(b)-F(a) или значение приращения любой первообразной от данной функции f(x) при изменении аргумента от x=a до x=b называется определенным интегралом функции f(x) в пределах от а до b : a ∫bf(x)dx =F(b)-F(a) это формула Ньютона-Лейбница Свойства определенного интеграла. 1. Определенный интеграл с равными пределами равен нулю: b∫af(x) dx= 0 2. При перемене местами пределов интегрирования величина определенного интеграла изменяется на противоположную: a∫bf(x) dx= - b∫af(x)dx 3. Если отрезок интегрирования [a,b] разделен на конечное число nчастичных отрезков [a,x1], [x1,x2],…..,[xn-1,b], то определенный интеграл от функции f(x) на отрезке [a,b]равен сумме определенных интегралов от этой функции на каждом из частичных отрезков (свойств аддитивности): a∫bf(x) dx= a ∫x1 f(x) dx + x1∫x2+ …….xn-1∫bf(x) dx 4. a∫bkf (x)dx = ka∫bf(x) dx , где k- постоянный множитель 5. Определенный интеграл от алгебраической суммы конечного числа функций, интегрируемых на отрезке [a,b], равен алгебраической сумме определенных интегралов этих функций на данном отрезке : a∫b[f1(x)+f2(x)+….+fn(x)]dx =a∫bf1(x)dx+a∫bf2(x)dx +…..a∫bfn(x)dx Геометрический смысл определенного интеграла. Плоская фигура, ограниченная сверху графиком непрерывной функции y=f(x), снизу –осью абцисс, слева-прямой линиейx=a, а справа – прямой линией x=b, называется криволинейной трапецией. Площадь криволинейной трапеции, ограниченной графиком функции y=f(x), осенью абцисс и прямыми линиями x=a и x=b,численно равна определенному интегралу от этой функции на отрезке[a,b]. В этом и заключается геометрическая интерпретация . 6.Понятие дифференциального уравнения. Порядок уравнения, общее и частное решение дифференциального уравнения. Дифференциальные уравнения первого порядка с разделяющимися переменными, алгоритм их решения. Понятие дифференциального уравнения. Уравнение, в общем случае связывающее искомую функцию y=f(x), ее аргумент x, а также производные различных порядков этой функции , называется обыкновенным дифференциальным уравнением. F( x, y, y', y'',……,y(n))=0 Порядок уравнения, общее и частное решение дифференциального уравнения. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в это уравнение. Общий вид дифференциального уравнения первого порядка : F(x,y, y')=0 Общим решениемдифференциального уравнения называется функция , удовлетворяющая двум условиям: во-первых, эта функция должна удовлетворять данному дифференциальному уравнению, т.е. при подстановке в уравнение должна обращать его в тождество; во-вторых, количество произвольных постоянных в этой функции должно быть равным порядку данного уравнения. Общее решения дифференциального уравнения n-го порядка имеет вид : y=F(x,C1,C2,…,Cn) Общее решение дифференциального уравнения 1_ого порядка имеет вид : y=F(x,С) В отличие от общего решения дифференциального уравнения его частным решениемназывают всякую функцию, удовлетворяющую данному уравнению, но не содержащую произвольных постоянных. Дифференциальные уравнения первого порядка с разделяющимися переменными, алгоритм их решения. Уравнение с разделяющимися переменными имеет вид ___________________ ,причем его правая часть может быть представлена в виде произведения двух отдельных функций :_______________________________________________________________ .Тогда: Можно преобразовать это уравнение ,разделив переменные справа и слева ; Общий вид уравнения с разделенными переменными : Уравнение решается непосредственным интегрированием :слева по переменной y и справа по переменной х с прибавлением постоянной С . Решая это уравнение найдем ответ : |
