10_Кластерный анализ. 10. 1 Процедура кластерного анализа 10 1 Основные понятия

• Название: 10. 1 Процедура кластерного анализа 10 1 Основные понятия
• Анкор: 10_Кластерный анализ.doc
• Дата: 17.12.2017
• Размер: 391 Kb.
• Имя файла: 10_Кластерный анализ.doc
• Тип: Решение; #11873
• страница: 6 из 7

10.5.2 Неиерархические методы кластерного анализа. Итеративные методы

При большом количестве наблюдений иерархические методы кластерного анализа непригодны. В таких случаях используют неиерархические методы, основанные на разделении, которые представляют собой итеративные методы дробления исходной совокупности. В процессе деления новые кластеры формируются до тех пор, пока не будет выполнено правило остановки.

Процесс неиерархической кластеризации всегда является итеративным. Итеративные методы кластеризации различаются выбором следующих параметров:

• 
  начальной точки;
  
• 
  правилом формирования новых кластеров;
  
• 
  правилом остановки.
  

Такая неиерархическая кластеризация состоит в разделении набора данных на определенное количество отдельных кластеров. Существует два подхода. Первый заключается в определении границ кластеров как наиболее плотных участков в многомерном пространстве исходных данных, т.е. определение кластера там, где имеется большое "сгущение точек". Второй подход заключается в минимизации меры различия объектов.

10.5.3 Алгоритм k-средних (k-means)

Наиболее распространен среди неиерархических методов алгоритм k-средних, также называемый быстрым кластерным анализом. В отличие от иерархических методов, которые не требуют предварительных предположений относительно числа кластеров, для этого метода необходимо иметь гипотезу о наиболее вероятном количестве кластеров.

Алгоритм -средних строит кластеров, расположенных на возможно больших расстояниях друг от друга. Выбор числа может базироваться на результатах предшествующих исследований, теоретических соображениях или интуиции.

Общая идея алгоритма: объекты распределяются по кластерам так, что средние в кластерах (для всех переменных) максимально возможно отличаются друг от друга.

Кластеризация осуществляется по следующему алгоритму:

1. 
   Выбор первоначальных центров кластеров:
   

Выбирается число кластеров . Каждому кластеру соответствует один центр. Выбор первоначальных центров может осуществляться одним из следующих способов:

• 
  выбор наблюдений из условия максимизации расстояния между ними;
  
• 
  случайный выбор наблюдений;
  
• 
  выбор первых наблюдений.
  

2. 
   Первоначальное распределение объектов по кластерам.
   

Каждый объект присоединяется к тому кластеру, расстояние до которого является наименьшим.

3. 
   Итеративный процесс.
   

Вычисляются центры кластеров, как покоординатные средние кластеров. Объекты опять перераспределяются. Процесс вычисления центров и перераспределения продолжается до тех пор, пока не будет выполнено одно из условий останова:

• 
  кластерные центры стабилизировались, т.е. все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации;
  
• 
  число итераций равно максимальному возможному заданному числу итераций.
  

На рис. 10.6 приведен пример работы алгоритма 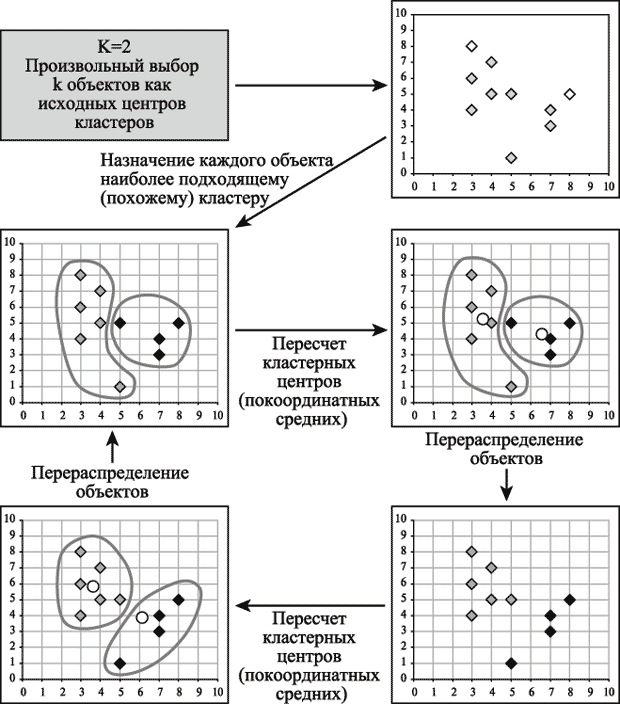-средних для , равного двум.



Рис. 10.6 Пример работы алгоритма -средних (=2)

После получений результатов кластерного анализа методом k-средних следует проверить правильность кластеризации (т.е. оценить, насколько кластеры отличаются друг от друга). Для этого рассчитываются средние значения для каждого кластера. При хорошей кластеризации должны быть получены сильно отличающиеся средние для всех измерений или хотя бы большей их части.

Достоинства алгоритма -средних:

• 
  простота использования;
  
• 
  быстрота использования;
  
• 
  понятность и прозрачность алгоритма.
  

Недостатки алгоритма k-средних:

• 
  алгоритм слишком чувствителен к выбросам, которые могут искажать среднее.
  
• 
  алгоритм может медленно работать на больших базах данных. Возможным решением данной проблемы является использование выборки данных.