10_Кластерный анализ. 10. 1 Процедура кластерного анализа 10 1 Основные понятия
 Скачать 391 Kb.
|
10.4 Меры расстояния и сходства между кластерами. Методы объединения кластеровПроцедура кластерного анализа предполагает объединение в группы объектов, наиболее сходных между собой, то есть тех, расстояние между которыми является наименьшим. Когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Однако если в каждый кластер входит группа объектов (два и более), то необходимо определить, как именно будет определяться расстояние между кластерами. Существуют различные правила определения расстояния между кластерами, называемые методами объединения или связи для двух кластеров. В кластер-процедурах используют понятия расстояния между группами объектов и меры близости двух групп объектов. Пусть  —  -я группа (класс, кластер), состоящая из  объектов;  — среднее арифметическое векторных наблюдений группы , т.е. «центр тяжести»;  — расстояние между группами  и  .Наиболее употребительными расстояниями и мерами близости между классами объектов являются: • расстояние, измеряемое по принципу «ближайшего соседа»: 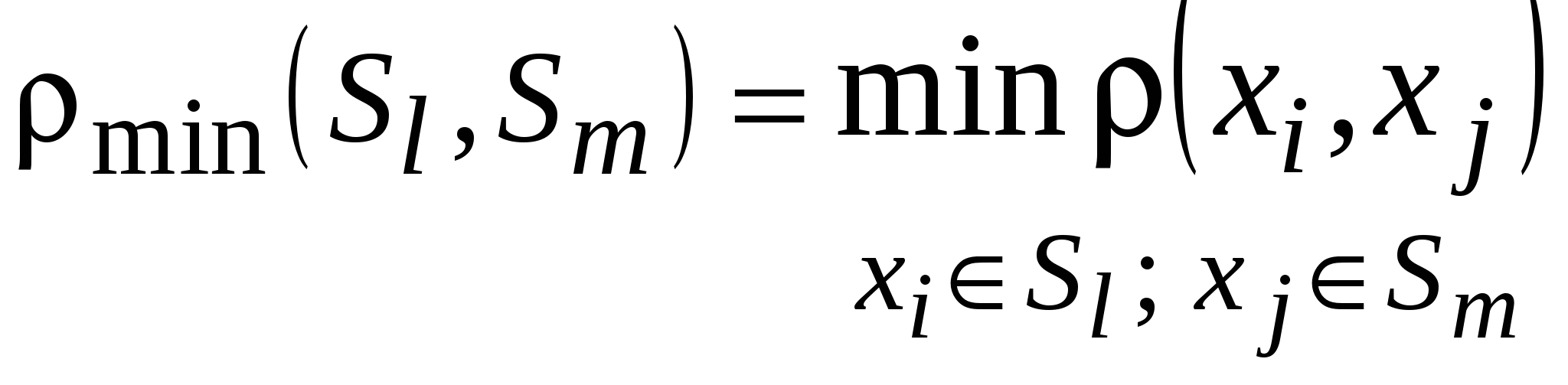 Здесь расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Этот метод позволяет выделять кластеры сколь угодно сложной формы при условии, что различные части таких кластеров соединены цепочками близких друг к другу элементов. В результате работы этого метода кластеры представляются длинными "цепочками" или "волокнистыми" кластерами, "сцепленными вместе" только отдельными элементами, которые случайно оказались ближе остальных друг к другу. • расстояние, измеряемое по принципу «дальнего соседа»: 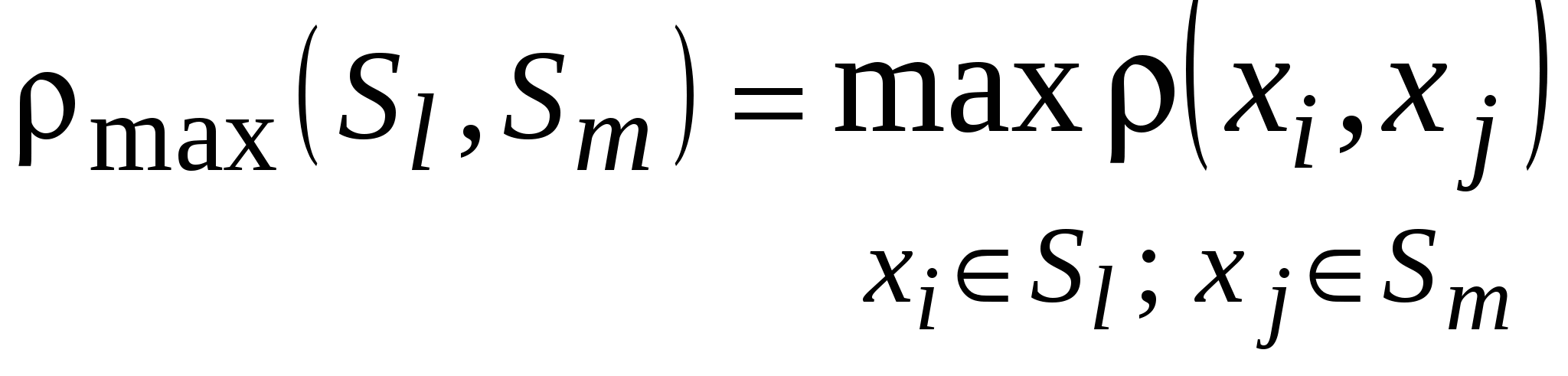 Здесь расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. "наиболее удаленными соседями"). Метод хорошо использовать, когда объекты действительно происходят из различных "рощ". Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является "цепочечным", то этот метод не следует использовать. • Невзвешенный центроидный метод (метод невзвешенного попарного центроидного усреднения - unweighted pair-group method using the centroid average (Sneath and Sokal, 1973)). В качестве расстояния между двумя кластерами в этом методе берется расстояние между их центрами тяжести.  где  — векторы средних соответственно Sl и Sm кластеров;Взвешенный центроидный метод (метод взвешенного попарного центроидного усреднения - weighted pair-group method using the centroid average, WPGMC (Sneath, Sokal 1973)). Этот метод похож на предыдущий, разница состоит в том, что для учета разницы между размерами кластеров (по числу объектов в них), используются веса. Этот метод предпочтительно использовать в случаях, если имеются предположения относительно существенных отличий в размерах кластеров. • расстояние, измеряемое по принципу «средней связи» (невзвешенного попарного среднего), определяемое как среднее арифметическое всех попарных расстояний между представителями рассматриваемых групп:  Этот метод следует использовать, если объекты действительно происходят из различных "рощ", в случаях присутствия кластеров "цепочного" типа, при предположении неравных размеров кластеров. Метод взвешенного попарного среднего (метод взвешенного попарного арифметического среднего - weighted pair-group method using arithmetic averages, WPGM A (Sneath, Sokal, 1973)). Этот метод похож на метод невзвешенного попарного среднего, разница состоит лишь в том, что здесь в качестве весового коэффициента используется размер кластера (число объектов, содержащихся в кластере). Этот метод рекомендуется использовать именно при наличии предположения о кластерах разных размеров. Метод Варда(Ward's method). В качестве расстояния между кластерами берется прирост суммы квадратов расстояний объектов до центров кластеров, получаемый в результате их объединения (Ward, 1963). В отличие от других методов кластерного анализа для оценки расстояний между кластерами, здесь используются методы дисперсионного анализа. На каждом шаге алгоритма объединяются такие два кластера, которые приводят к минимальному увеличению целевой функции, т.е. внутригрупповой суммы квадратов. Этот метод направлен на объединение близко расположенных кластеров и "стремится" создавать кластеры малого размера. |