10_Кластерный анализ. 10. 1 Процедура кластерного анализа 10 1 Основные понятия
 Скачать 391 Kb.
|
10.3 Меры расстояния и сходства между объектамиОбычно исходные данные представляют в виде матрицы измеренных значений признаков для рассматриваемых объектов 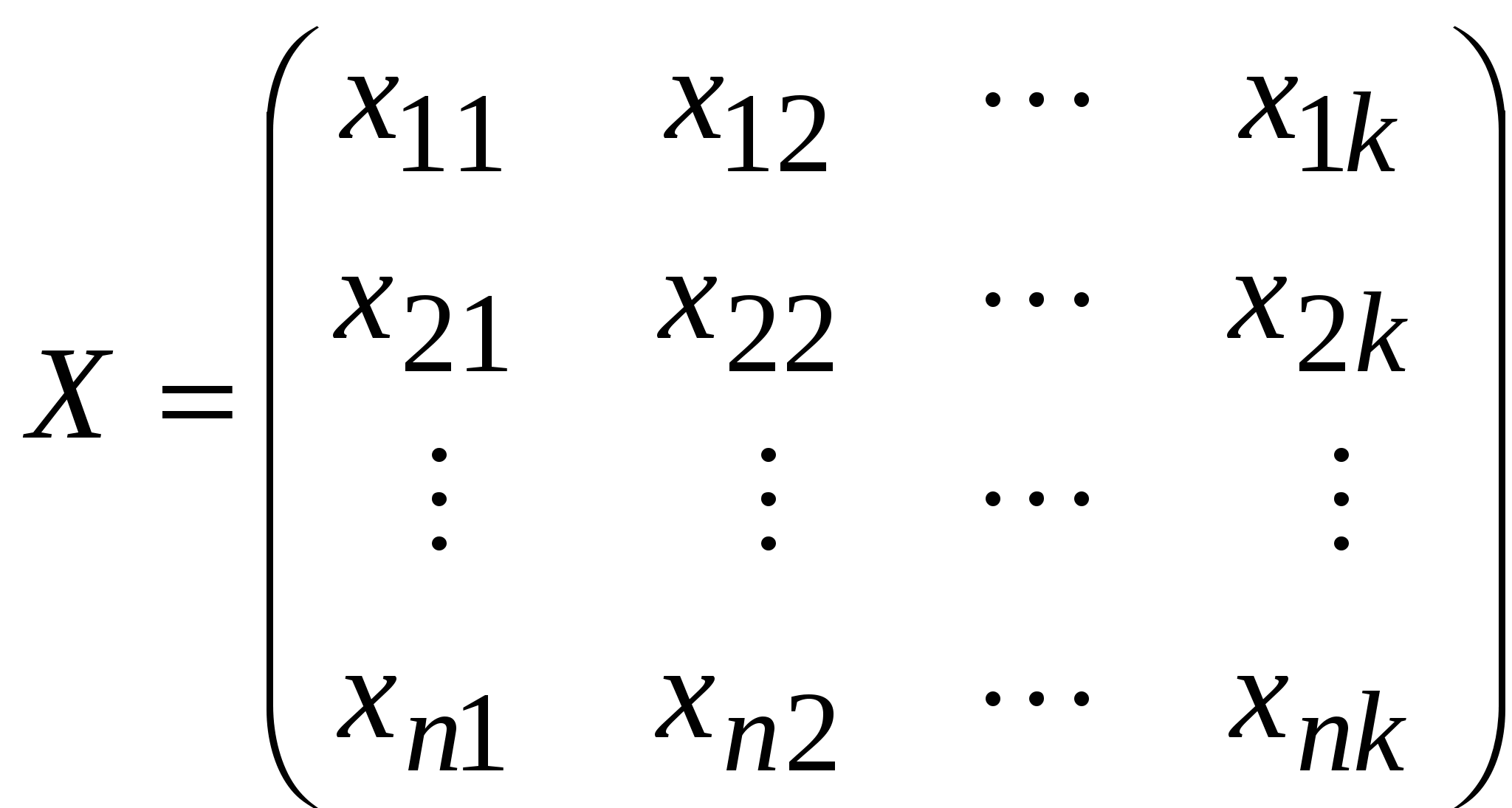 .В то же время большинство алгоритмов кластерного анализа основывается на исследовании матрицы расстояний. Поэтому первым этапом решения задачи кластеризации является выбор способа вычисления расстояний между объектами или признаками. Наиболее трудным и наименее формализованным в задаче классификации является определение понятия однородности объектов. В общем случае понятие однородности объектов задается введением либо правила вычисления расстояний  между любой парой исследуемых объектов из совокупности, либо некоторой функцией  , характеризующей степень близости i-го и j-го объектов.Выбор метрики, или меры близости, является нетривиальным и одним из основных моментом исследования, от которого в значительной степени зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. В каждом конкретном случае этот выбор должен производиться по-своему, в зависимости от целей исследования, физической и статистической природы наблюдений, априорных сведений о характере вероятностного распределения  .Для метрических величин наиболее часто используют: 1. Обычное евклидово расстояние между  -тым и  -тым объектами определяется по формуле где  — значения  -го признака -того и -того объектов ( ;  ).Оно используется в следующих случаях: - наблюдения берутся из генеральной совокупности, имеющей многомерное нормальное распределение, т.е. исходные признаки взаимно независимы и имеют близкие значения дисперсий; - исходные признаки однородны по физическому смыслу и одинаково важны для классификации. 2. «Взвешенное» евклидово расстояние определяется из выражения  Оно применяется в тех случаях, когда каждой -ой компоненте вектора (-тому признаку) наблюдений удается приписать некоторый «вес»  , пропорциональный степени важности признака в задаче классификации. Определение весов связано с дополнительными исследованиями, например с организацией опроса экспертов и обработкой их мнений. Определение весов только по данным выборки может привести к ложным выводам.3. Квадрат евклидова расстояния.  Для придания больших весов расстояниям между более отдаленными друг от друга объектами можем воспользоваться квадратом евклидова расстояния. 4. Манхэттенское расстояние (расстояние городских кварталов), также называемое "хэмминговым" или "сити-блок" расстоянием. Это расстояние рассчитывается как сумма разностей по координатам (путь, который должен преодолеть Манхэттенский таксист, чтобы проехать от одного дома к другому по улицам, пересекающимся под прямым углом). В большинстве случаев эта мера расстояния приводит к результатам, подобным расчетам расстояния евклидова расстояния. Однако при использовании этой меры влияние отдельных выбросов меньше, чем при использовании евклидова расстояния, поскольку здесь координаты не возводятся в квадрат. Часто используется как мера различия объектов, задаваемых дихотомическими признаками. Это расстояние определяется по формуле  .Если все признаки дихотомические, то оно равно числу несовпадений значений соответствующих признаков в рассматриваемых -том и -том объектах. 3. Расстояние Чебышева. Это расстояние стоит использовать, когда необходимо определить два объекта как "различные", если они отличаются по какому-то одному измерению. Расстоянием между двумя наблюдениями является абсолютное значение максимальной разности последовательных пар переменных, соответствующих этим наблюдениям. 4. Расстояние Минковского равно корню r-ой степени из суммы абсолютных разностей пар значений взятых в r-ой степени: 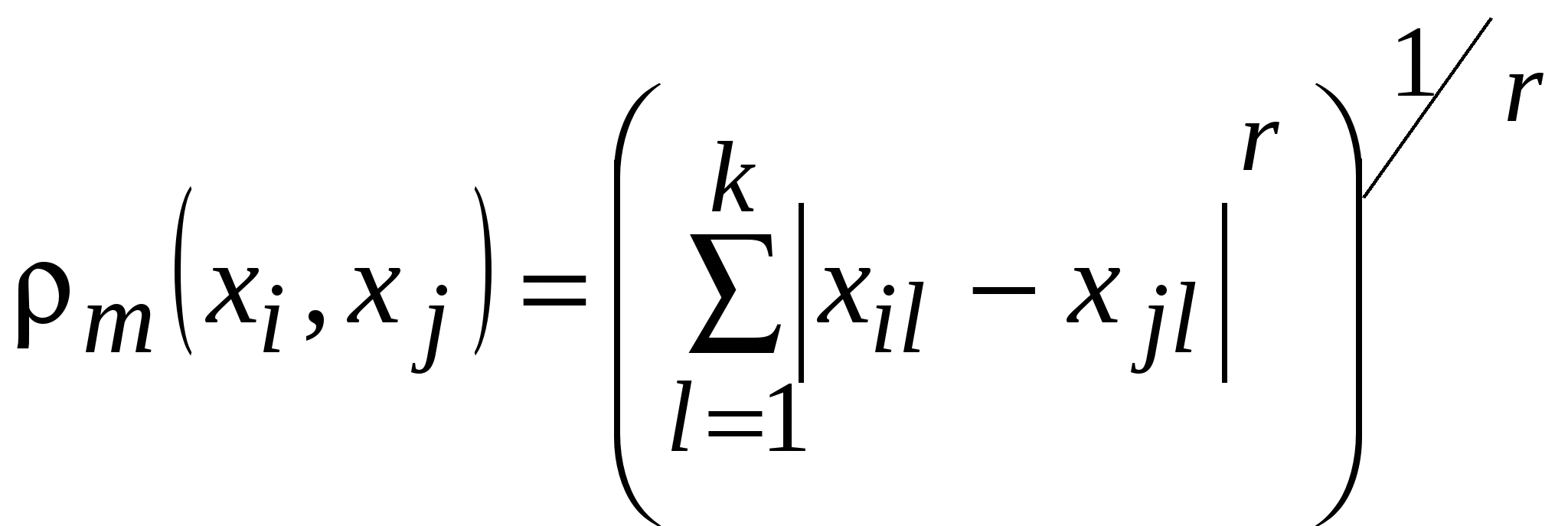 Показатель  можно выбрать в пределах от 1 до 4. Если  , то получим евклидово расстояние.5. Это обобщенный вариант расстояния Минковского. Это расстояние, называемое также степенным расстоянием, равно корню 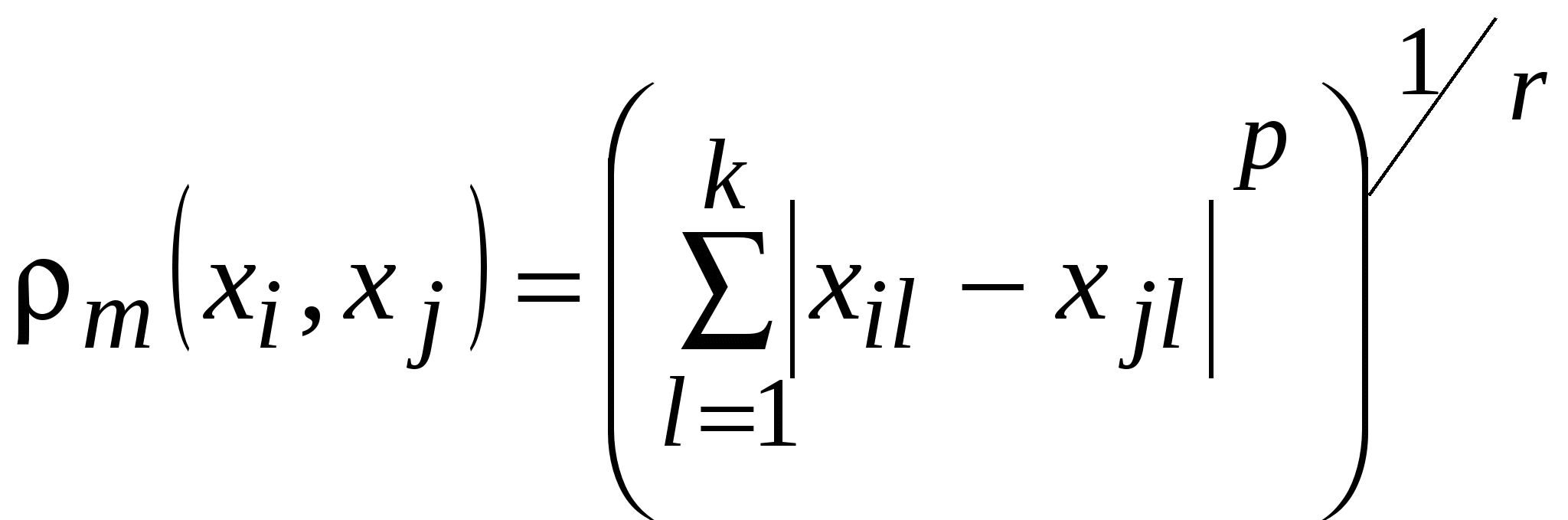-ой степени из суммы абсолютных разностей пар значений взятой в  -ой степени: ,где и могут принимать значения от 1 до 4.Для данных, измеренных по номинальной шкале, используются: 1. Процент несогласия. Это расстояние вычисляется, если все данные являются категориальными.  Например, первый признак объекта – пол, второй – возрастная группа, третий – должность. Представим значения свойств (признаков) объекта в виде вектора значений. Первый вектор – (муж, 20 лет, учитель), второй вектор – (муж, 28 лет, менеджер). Процент несогласия равен 2/3. Эти вектора различаются на 66.6%. 2. Мера хи-квадрат. Для того чтобы найти расстояние между двумя наблюдениями, сравнивают частоты выпадения переменных, относящихся к этим наблюдениям. Квадратный корень из значения хи-квадрат будет применяться в качестве дистанционной меры (меры сходства). 3. Мера фи-квадрат. Эта мера представляет собой попытку нормализации меры хи-квадрат. Для этого она делится на квадратный корень общей суммы частот. Бинарные переменные. Здесь, как правило, речь идёт о переменных, которые указывают на факт осуществления некоторого события или выполнения определённого критерия. Это обстоятельство должно быть закодировано при помощи двух численных значений. Если сопоставить друг с другом две переменные, то все возможные сочетания наблюдений дают четыре различные частоты (таблица сопряженности): На основании этих частот, можно рассчитать множество различных дистанционных мер, например:
|