10_Кластерный анализ. 10. 1 Процедура кластерного анализа 10 1 Основные понятия
 Скачать 391 Kb.
|
10.1.3 Оценка качества кластеризацииОценка качества кластеризации может быть проведена на основе следующих процедур:
10.1.4 Области применения кластерного анализаКластерный анализ применяется в различных областях, если нужно классифицировать большое количество информации, при этом априорная информация о существовании групп отсутствует. Так, в медицине используется кластеризация заболеваний, лечения заболеваний или их симптомов, а также таксономия пациентов, препаратов и т.д. В археологии устанавливаются таксономии каменных сооружений и древних объектов и т.д. В маркетинге это может быть задача сегментации конкурентов и потребителей, поставщиков, товаров. Одной из наиболее важных задач при применении кластерного анализа в маркетинговых исследованиях является анализ поведения потребителя, а именно: группировка потребителей в однородные классы для получения максимально полного представления о поведении клиента из каждой группы и о факторах, влияющих на его поведение. Важной задачей, которую может решить кластерный анализ, является позиционирование, т.е. определение ниши, в которой следует позиционировать новый продукт, предлагаемый на рынке. В результате применения кластерного анализа строится карта, по которой можно определить уровень конкуренции в различных сегментах рынка и соответствующие характеристики товара для возможности попадания в этот сегмент. С помощью анализа такой карты возможно определение новых, незанятых ниш на рынке, в которых можно предлагать существующие товары или разрабатывать новые. Кластерный анализ также может быть удобен, например, для анализа клиентов компании. Для этого все клиенты группируются в кластеры, и для каждого кластера вырабатывается индивидуальная политика. Такой подход позволяет существенно сократить объекты анализа, и, в то же время, индивидуально подойти к каждой группе клиентов. В менеджменте примером задачи кластеризации будет разбиение персонала на различные группы, классификация потребителей и поставщиков, выявление схожих производственных ситуаций, при которых возникает брак. В социологии задача кластеризации - разбиение респондентов на однородные группы.  10.2 Исходные данные для процедуры кластерного анализаДопустим, имеется набор данных 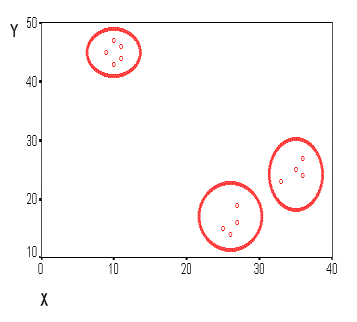 , включающий несколько наблюдений, каждое из которых характеризуется двумя признаками  и  . Данные по ним могут быть представлены в виде диаграммы рассеивания (рис. 10.2.) Каждое наблюдение представляет собой точку на плоскости. Рис. 10.2 Диаграмма рассеивания переменных и .Наблюдения (объекты), которые по значениям и "похожи" друг на друга, принадлежат к одной группе (кластеру); объекты из разных кластеров не похожи друг на друга.Критерием для определения схожести и различия кластеров является расстояние между точками на диаграмме рассеивания. Существует несколько способов определения меры расстояния (или меры близости) между кластерами. Наиболее распространенный способ - вычисление евклидова расстояния между двумя точками. В двумерном признаковом пространстве оно определяется по формуле:  В пространстве трех измерений (такая ситуация представлена на рис. 10.3, формула приобретает вид: 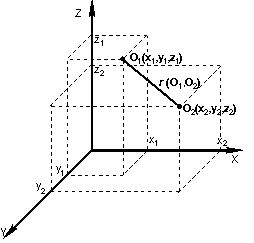   Рис. 10.3. Расстояние между двумя точками в пространстве трех измерений В общем случае переменные, характеризующие признаки, измеряются по разным шкалам и их численные значения могут существенно отличаться друг от друга. При расчете величины расстояния между точками, отражающими положение объектов в пространстве их свойств, переменная, имеющая большие значения, будет практически полностью доминировать над переменной с малыми значениями. Таким образом, из-за неоднородности единиц измерения признаков становится невозможно корректно рассчитать расстояния между точками. Эта проблема решается при помощи предварительной стандартизации переменных. Стандартизация (standardization) или нормирование (normalization) приводит значения всех преобразованных переменных к единому диапазону значений путем выражения через отношение этих значений к некой величине, отражающей определенные свойства конкретного признака. Существуют различные способы нормирования исходных данных. Наиболее распространенные способы:
 ;  ;
Однако эта операция может привести к нежелательным последствиям. Если кластеры хорошо разделимы по одному признаку и не разделимы по другому, то после нормирования дискриминирующие возможности первого признака будут уменьшены в связи с усилением «шумового» эффекта второго. Наряду со стандартизацией переменных, существует вариант придания каждой из них определенного коэффициента важности, или веса, который бы отражал значимость соответствующей переменной. В качестве весов могут выступать экспертные оценки, полученные в ходе опроса экспертов - специалистов предметной области. Полученные произведения нормированных переменных на соответствующие веса позволяют получать расстояния между точками в многомерном пространстве с учетом неодинакового веса переменных. В ходе экспериментов возможно сравнение результатов, полученных с учетом экспертных оценок и без них, и выбор лучшего из них. |
;
.