10_Кластерный анализ. 10. 1 Процедура кластерного анализа 10 1 Основные понятия
 Скачать 391 Kb.
|
|
10. Кластерный анализ 10.1 Процедура кластерного анализа10.1.1 Основные понятия.Пусть исследуется совокупность  объектов, каждый из которых характеризуется  измеренными признаками. Требуется разбить эту совокупность на однородные в некотором смысле группы. При этом практически отсутствует априорная информация о характере распределения -мерного вектора  внутри классов. Полученные в результате разбиения группы обычно называются кластерами (таксонами, образами), методы их нахождения — кластер-анализом (численной таксономией или распознаванием образов с самообучением).Решение задачи заключается в определении естественного расслоения результатов наблюдений на четко выраженные кластеры, лежащие друг от друга на некотором расстоянии. (Может оказаться, что множество наблюдений не обнаруживает естественного расслоения на кластеры, т.е. образует один кластер). Обычной формой представления исходных данных в задачах кластерного анализа служит матрица 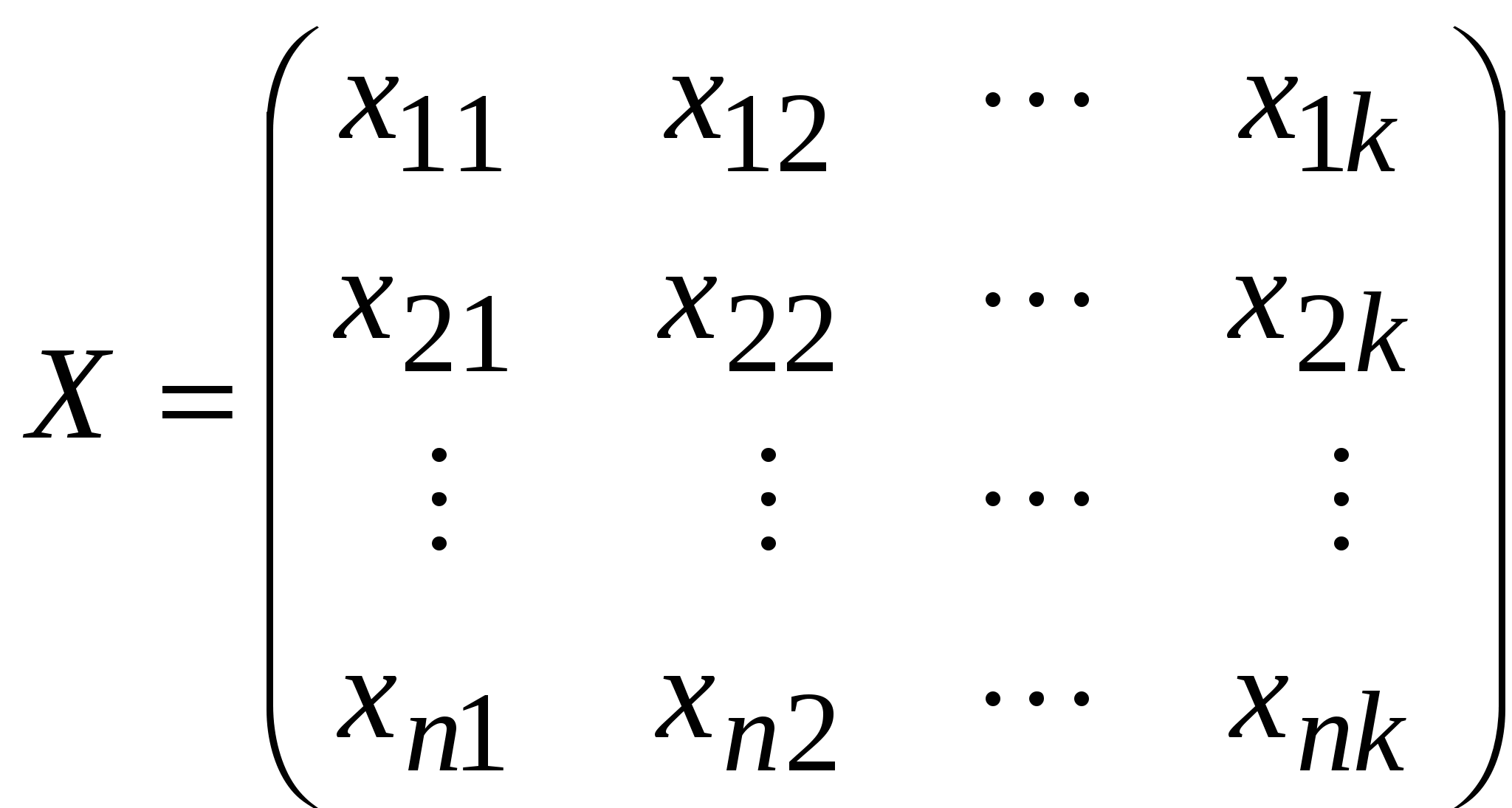 ,каждая строка которой представляет результаты измерений рассматриваемых признаков у одного из объектов. Кластеризация предназначена для разбиения совокупности объектов на однородные группы (кластеры или классы). Если данные выборки представить как точки в признаковом пространстве, то задача кластеризации сводится к определению "сгущений точек". Переводится понятие кластер (cluster) как "скопление", "гроздь". Синонимами термина " кластеризация " являются "автоматическая классификация ", "обучение без учителя" и "таксономия". Цель кластеризации - поиск существующих структур. Кластеризация является описательной процедурой, она не делает никаких статистических выводов, но дает возможность провести разведочный анализ и изучить "структуру данных". Классы заранее не определены, осуществляется поиск наиболее похожих, однородных групп. Кластер можно охарактеризовать как группу объектов, имеющих общие свойства. Характеристиками кластера можно назвать два признака:
Кластеры могут быть непересекающимися, или эксклюзивными (non-overlapping, exclusive), и пересекающимися (overlapping). Схематическое изображение непересекающихся и пересекающихся кластеров дано на рис. 10.1. 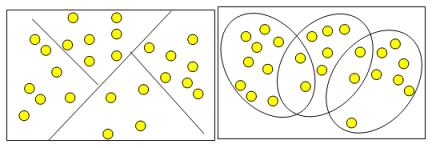 Рис. 10.1 Непересекающиеся и пересекающиеся кластеры Термин «кластерный анализ», впервые введенный Трионом (Tryon) в 1939 году, объединяет более 100 различных алгоритмов. В отличие от задач классификации, кластерный анализ не требует априорных предположений о наборе данных, не накладывает ограничения на представление исследуемых объектов, позволяет анализировать показатели различных типов данных (интервальные данные, частоты, бинарные данные). При этом необходимо помнить, что переменные должны измеряться в сравнимых шкалах. 10.1.2 Характеристики кластераКластер имеет следующие математические характеристики: центр, радиус, среднеквадратическое отклонение, размер кластера. Каждый объект совокупности в кластерном анализе рассматривается как точка в заданном признаковом пространстве. Значение каждого из признаков у данной единицы служит ее координатой в этом пространстве. Центр кластера - это среднее геометрическое место точек в пространстве переменных. Радиус кластера - максимальное расстояние расположения точек от центра кластера. Если невозможно при помощи математических процедур однозначно отнести объект к одному из двух кластеров, то такие объекты называют спорными, и обнаруживается перекрытие кластеров. Спорный объект - это объект, который по мере сходства может быть отнесен к нескольким кластерам. Размер кластера может быть определен либо по радиусу кластера, либо по среднеквадратичному отклонению объектов для этого кластера. Объект относится к кластеру, если расстояние от объекта до центра кластера меньше радиуса кластера. Если это условие выполняется для двух и более кластеров, объект является спорным. Неоднозначность данной задачи может быть устранена экспертом или аналитиком. |