книга цивадзе. 11 Общие сведения о комплексных соединениях 11 Состав комплексных соединений
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
Вопросы11.10. Перечислите достоинства и недостатки метода валентных связей (ВС) (применительно к комплексным соединениям). 11.11. Определите диамагнитные и парамагнитные комплексы: а) [Co(NH3)6]3; б) [TiF6]3–; в) [TiCl6]2–; г) [CuCl5]3–; д) [Cu(OH)6]4–; е) [V(H2O)6]3; ж) [VCl4]–; з) [VF6]–; и) [Cu(CN)4]2–. 11.4.2. Теория кристаллического поляДля предсказания строения комплексных соединений d-элементов хорошим дополнением к методу валентных связей оказалась теория кристаллического поля (КП). Основы этой теории были разработаны Бете в 1929 г. при рассмотрении эффекта замещения катиона натрия в решетке ионного кристалла типа NaCl. Бете показал, что при помещении свободного иона в электростатическое поле (так называемое кристаллическое поле), существующее в кристалле, происходит полное или частичное снятие вырождения энергетических подуровней иона, т. е. их расщепление. Согласно теории кристаллического поля, вокруг положительно заряженного центрального иона упорядоченно располагаются точечные лиганды, которые заряжены отрицательно. Число этих точечных отрицательных зарядов определяет симметрию системы (комплекса). Реальный объем лигандов, а также их геометрическое и электронное строение во внимание не принимаются. Взаимодействие центрального атома с лигандами рассматривается с позиций квантовой механики. Энергия свободного (несвязанного) иона определяется кинетической энергией системы, энергией взаимодействия электрона с ядром, а также энергией межэлектронного и спин-орбитального взаимодействия6. При помещении иона в кристаллическое поле той или иной геометрии, которая зависит от симметрии системы в целом, на энергию системы дополнительно влияет потенциал V кристаллического поля. В теории кристаллического поля чаще рассматривают поля октаэдрической и тетраэдрической симметрии. В поле сферической симметрии все орбитали d-подуровня свободных ионов переходных металлов вырождены (имеют одинаковую энергию). В электростатическом поле более низкой симметрии d-орбитали неэквивалентны по энергии (происходит расщепление подуровней, т. е. частичное снятие вырождения энергии). Расщепление подуровней в поле октаэдрической симметрии показано на рис. 11.10. Атомные dJ-орбитали (dx2−y2 и dz2 ) симметрии eg ближе всего подходят к орбиталям лигандов и подвер-  Рис. 11.10. Расщепление d-подуровня в кристаллическом поле октаэдрической симметрии гаются наиболее сильному воздействию их электростатического поля. Возникновение сил отталкивания приводит к увеличению энергии egорбиталей (они дестабилизируются). Три другие d-АО (dху, dxz, dyz) симметрии t2g, называемые dH, располагаются между орбиталями лигандов, поэтому их энергия понижается (орбитали стабилизируются). Разность энергий eg- и t2g-состояний часто обозначают7 как 10Dq. Dq — это радиальный интеграл, который зависит от эффективного заряда и порядкового номера центрального иона Mn+, а также от расстояния металл—лиганд. В спектроскопии неорганических соединений величину Dq обычно называют основным параметром расщепления электронных конфигураций. Характер расщепления определяется симметрией кристаллического поля и числом d-электронов иона переходного металла. Большое значение имеет также тип кристаллического поля, который зависит от природы лигандов. Чем сильнее поле лигандов, тем больше энергия расщепления. Обычно рассматривают два крайних случая — слабое и сильное кристаллические поля. В слабом поле потенциал межэлектронного взаимодействия существенно больше потенциала кристаллического поля и, тем более, потенциала спин-орбитального взаимодействия. Координационные соединения с лигандами, создающими слабые кристаллические поля, называют высокоспиновыми (в методе ВС такие соединения называют спин-свободными (внешнеорбитальными) или ионными комплексами). В сильном поле потенциал V заметно превышает потенциалы межэлектронного и спин-орбитального взаимодействий и поэтому подавляет их. Координационные соединения с лигандами, создающими сильные кристаллические поля, называют низкоспиновыми (в методе ВС им соответствуют спин-связанные (внутриорбитальные) или ковалентные комплексы). В зависимости от силы поля лигандов заселение орбиталей электронами происходит по-разному. В слабом поле, в соответствии с правилом Хунда, сначала (t2g- и eg-орбитали) последовательно заселяются одним электроном, и лишь после этого начинается заселение вторыми электронами наиболее низких по энергии t2g-орбиталей (рис. 11.11). В сильном поле прежде всего полностью заселяются t2g-орбитали, а уже потом eg-орбитали. 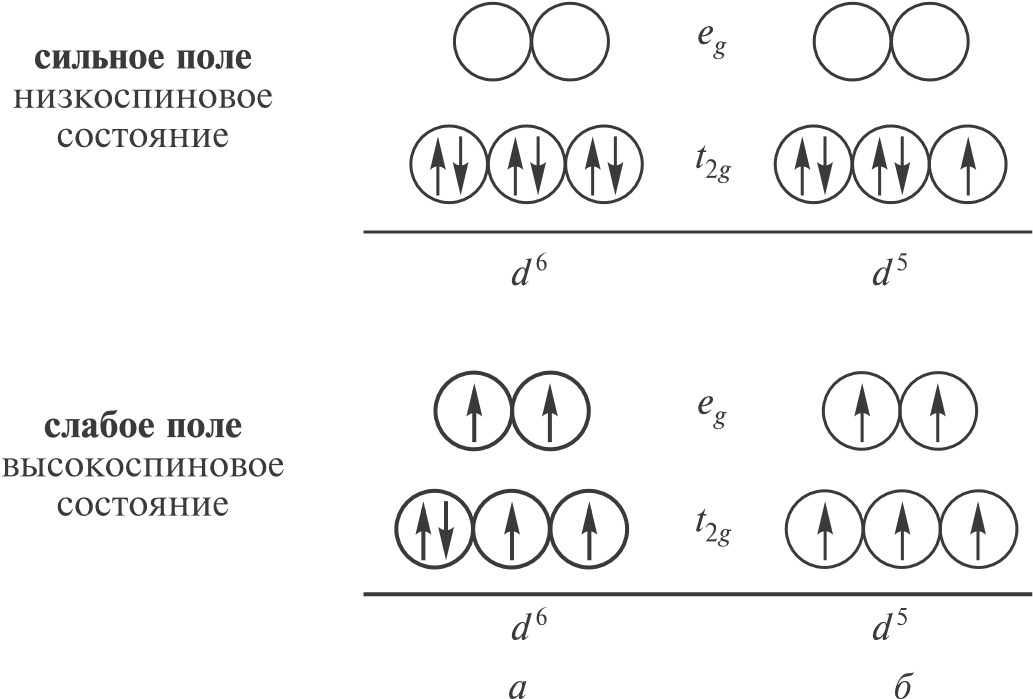 Рис. 11.11. Заселение орбиталей электронами в сильном (а) и слабом (б) тетраэдрических кристаллических полях на примере d 5- и d 6-конфигураций Соответствующие энергетические состояния характеризуют через заселенности t2g- и еg-орбиталей (например, t e25g g0). При eg–t2g-расщеплении энергия eg-орбиталей (и их электронов) повышается на 6Dq, а энергия t2g-орбиталей понижается на 4Dq. В итоге энергия системы в целом уменьшается; этот энергетический выигрыш называют энергией стабилизации кристаллическим полем8 (ЭСКП, обозначается δ). Величина ЭСКП зависит от числа электронов на eg- и t2gорбиталях и во многом определяет главные свойства комплексного соединения. Для октаэдрического поля ЭСКП (δ) рассчитывается по формуле: δ = n(4Dq) – m(6Dq) где n — число электронов на t2g-подуровне, m — число электронов на egподуровне. Например, ЭСКП для конфигурации t e23g g0: δ = (4Dq) ⋅ 3 = 12Dq а для конфигурации t e23g g2: δ = (4Dq) ⋅ 3 – (6Dq) ⋅ 2 = 0 В случае сильного поля расчет аналогичен, однако необходимо учитывать иной порядок заполнения орбиталей, например для ЭСКП конфигу- рации t e25g g0: δ = (4Dq) ⋅ 5 = 20Dq Таблица 11.2 Значения ЭСКП (Dq) для разных октаэдрических комплексов
Для электронных конфигураций d 0 и d10, а также в случае слабого поля лигандов, для конфигурации d 5, ЭСКП равна нулю (табл. 11.2). При точном расчете ЭСКП нужно также учитывать, что для заселения одной и той же орбитали двумя электронами с противоположными спинами необходимо затратить энергию на преодоление отталкивания электронов (табл. 11.3). Эту величину называют энергией спин-спаривания (Р ). Таблица 11.3 Энергия спин-спаривания и энергия расщепления для некоторых октаэдрических комплексов d-элементов
Порядок заселения d-орбиталей определяет число неспаренных электронов и, следовательно, магнитные свойства комплексных соединений. Для комплексов 3d-элементов эффективный магнитный момент (μэфф) в магнетонах Бора (μB) близок к значению, вычисленному по формуле для «чисто спинового случая» (без учета остальных составляющих):  μэфф = n n( + 2) μэфф = n n( + 2)где n — число неспаренных электронов. Экспериментальные магнитные моменты комплексов 4d- и 5d-элементов нередко отличаются от значений, рассчитанных по этому уравнению. При понижении симметрии комплекса происходит дальнейшее расщепление d-подуровней. В частности, при тетрагональном искажении октаэдра (растяжении или сжатии вдоль оси четвертого порядка с образованием тетрагональной бипирамиды) появляются невырожденные (а-, b-) уровни и двукратно вырожденный е-уровень (рис. 11.12). Полное удаление аксиальных лигандов с образованием плоскоквадратного комплекса приводит к тому, что энергия b2g-уровня (dxy-орбиталь) станет выше энергии a2gуровня (dz2 -орбиталь). 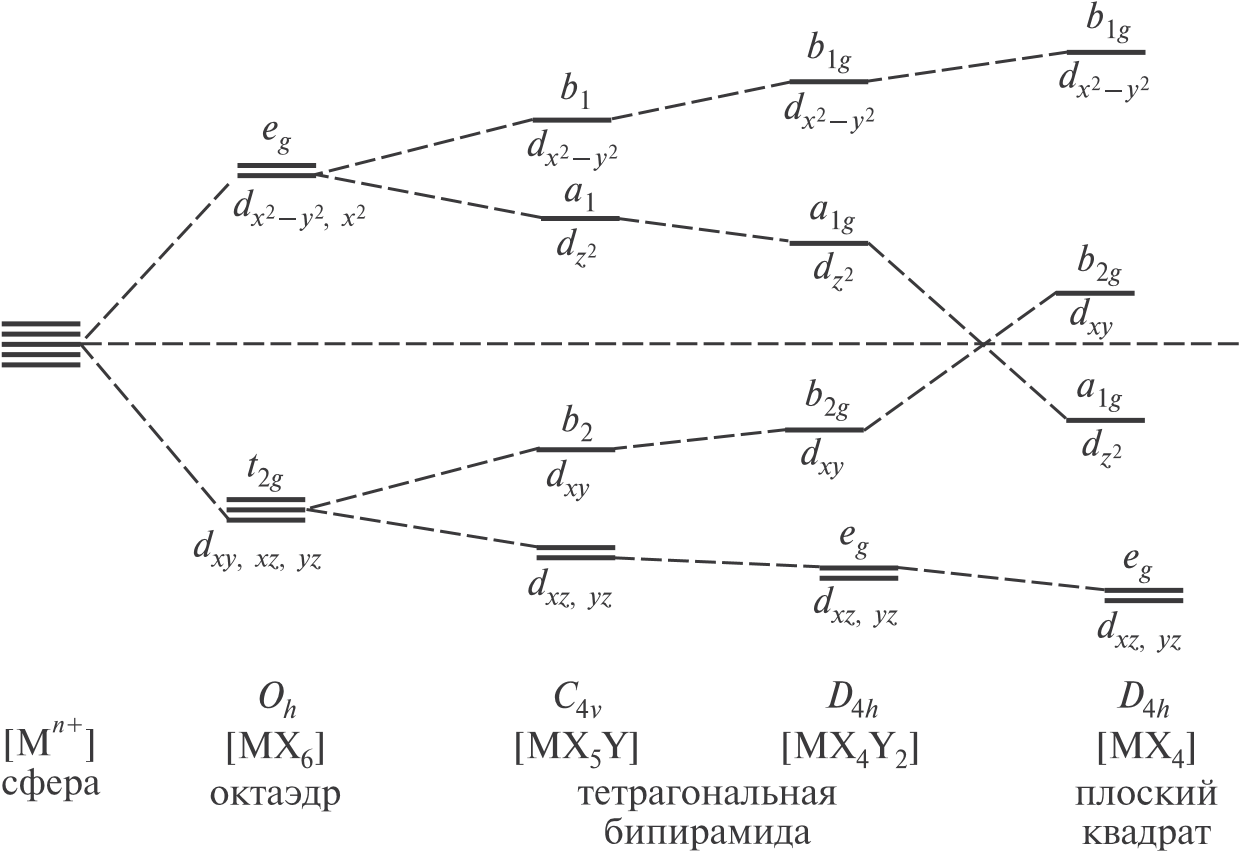 Рис. 11.12. Расщепление d-подуровня комплексообразователя при понижении симметрии октаэдрического кристаллического поля Искажение правильного координационного полиэдра (например, октаэдра) обычно связывают либо с наличием в этом полиэдре разных лигандов, либо с действием электростатических сил, либо с эффектом Яна9–Теллера10. По Яну–Теллеру, если нижнему по энергии электронному состоянию системы соответствуют два эквивалентных (вырожденных) энергетических уровня, то из-за искажения геометрии комплекса (понижения симметрии) вырождение снимается и как следствие понижается общая энергия системы. Эффект Яна–Теллера обычно иллюстрируют на примере комплексов меди(II). Катион меди(II) имеет электронную конфигурацию d 9, при которой (в присутствии шести одинаковых лигандов) двукратно вырожденные орбитали типа eg содержат три электрона; это обусловливает тетр агональное искажение геометрии комплекса. Для иона Cu(II) не получено соединений с неискаженной шестикоординационной геометрией. Для шестикоординационных комплексов с центральными ионами Au2 и Ag2 также наблюдается либо сжатие, либо растяжение октаэдра (вдоль оси симметрии 4-го порядка). Часто образуются псевдооктаэдры с четырьмя короткими (в экваториальной плоскости) и двумя длинными (аксиальными) связями. В предельном случае возможно сильное удлинение аксиальных связей металл—лиганд и образование плоскоквадратных комплексов с КЧ = 4. Искажение по Яну–Теллеру характерно также для комплексов ионов с электронной конфигурацией d 4 (например, тетрагонально искаженный комплекс [Сr(Н2О)6]2). В тетраэдрических комплексах расщепление энергетических уровней отличается от описанного для октаэдрических комплексов. В этом случае орбитали dx2−y2 и dz2 энергетически более выгодны (e-уровень), орбитали dxy, dxz и dyz менее выгодны (t2g-уровень), а переход к антипризме приводит к расщеплению обоих энергетических уровней. При самой симметричной геометрии комплекса, когда формируется икосаэдр, d-орбитали полностью вырождаются (рис. 11.13). В тетраэдрическом поле параметр расщепления значительно меньше, чем в октаэдрическом (Δt = (4 / 9)Δo), поэтому низкоспиновые конфигу-  Рис. 11.13. Расщепление d-подуровня в кристаллическом поле тетраэдрической и родственной симметрии рации в тетраэдрических системах встречаются редко; в кубическом поле Δc = (8 / 9)Δo. Характер расщепления в различных полях заметно влияет на строение и свойства комплексов (прежде всего, на их устойчивость). Так, в отличие от слабого октаэдрического поля, где в соответствии со значениями ЭСКП наиболее стабильны комплексы металлов с электронными конфигурациями d 3 и d 8, в слабом тетраэдрическом поле максимальные значения ЭСКП наблюдаются для электронных конфигураций d 2 и d 7. Это проявляется, в частности, в предпочтительных значениях координационного числа и форме координационного полиэдра комплекса. Например, Со(II) (d 7) часто образует тетраэдрические комплексы, а Ni(II) (d 8) к этому не склонен. В отсутствие ЭСКП (при соответствующих d-конфигурациях комплексообразователей) для комплексов характерны лишь октаэдрические (шесть лигандов) и тетраэдрические (четыре лиганда) полиэдры. Например, в ионах [FеСl4]–, [Cd(NH3)4]2 реализуется тетраэдрическая координация. Параметр расщепления зависит не только от симметрии, но и от природы и степени окисления комплексообразователя и от свойств лиганда. С возрастанием степени окисления центрального атома параметр расщепления увеличивается, так как лиганды сильнее притягиваются к центральному атому и в бо[льшей степени расщепляют d-подуровень. Для большинства d-элементов четвертого периода при изменении степени окисления от М2 до М3 параметр расщепления увеличивается приблизительно в 1,5 раза (табл. 11.4). Таблица 11.4 Значения параметра расщепления Δo комплексов с центральными ионами М2 и М3
Различия в величине параметра расщепления в пределах одного периода невелики; вниз по группе наблюдается его заметное увеличение. Параметр расщепления в комплексах 4d-элементов на 50% выше, чем для 3d-элементов, а в комплексах 5d-элементов — на 75%. Поэтому большинство комплексов элементов пятого и шестого периодов низкоспиновые. По способности увеличивать параметр расщепления лиганды располагают в ряд, получивший название спектрохимического: I– < Br– < CrO24− < S2– < N3− < F– < ur < OH– < IO3− < C O2 42− < < O2– < H2O < O22− < SCN– < py < NH3 < en < SO32− < NO2− < < bipy < o-phen < CN– < PH3 < CO где ur — мочевина (карбамид); py — пиридин; en — этилендиамин; bipy — α,α'-дипиридил; o-phen — о-фенантролин. В теории кристаллического поля электронное строение лигандов не принимают во внимание, поэтому эта теория не объясняет последовательность изменения свойств лигандов в спектрохимическом ряду, который был составлен по экспериментальным данным. Для определения параметра расщепления обычно используют электронную спектроскопию, спектроскопию электронного парамагнитного резонанса и другие физико-химические методы, с помощью которых можно наблюдать переходы электронов с одних d-орбиталей на другие (например, для конфигураций d11 и d 6 в октаэдрических комплексах с t2g-орбиталей на egорбитали). Все электронные переходы с энергией, попадающей в видимую область спектра (от 13000 до 24000 см–1, т. е. от 750 до 430 нм, от 1,61 до 2,97 эВ, от 37,1 до 68,5 ккал / моль, от 155 до 286 кДж / моль), придают веществу определенную окраску. В простых случаях, когда в видимой области спектра наблюдаются только одна-две полосы поглощения, используя теорию КП, можно предсказывать и окраску комплекса, и ее изменение при замещении лигандов. Например, в спектре [Тi(Н2О)6]3 переходу t2g—eg отвечает максимум поглощения при λ = 497 нм. Замена в этом комплексе всех молекул воды на оксалат-ионы (комплекс [Ti(C2O4)3]3–) вызывает сдвиг полосы поглощения хромофора1 до λ = 416 нм, а замена на ацетилацетон (комплекс [Ti(acac)3]) — λ = 592 нм. Согласно табл. 11.5, следует ожидать следующую окраску этих комплексов титана: аквакомплекс красный, оксалатный — желтый, ацетилацетонатный — синий. Однако в действительности аквакомплекс титана(III) красно-фиолетовый, потому что кроме основной полосы поглощения в его спектре наблюдается дополнительная полоса при λ = 570 нм (с примерно такой же интенсивности), которая и вносит в окраску фиолетовый компонент12. В спектрах двух других комплексов присутствует только основная полоса, и окраска этих комплексов совпадает с той, которая здесь предсказана. Комплексы ионов с электронной конфигурацией d 0 или d10 (например, SсIII и ZnII), для которых d—d-переходы невозможны, бесцветны, если сами лиганды не окрашены. С помощью теории КП можно также предсказать распределение ионов в тетраэдрических и октаэдрических полостях плотнейшей упаковки атомов кислорода в сложных оксидах типа шпинелей М М O2+ 32+ 4. В «нормальных» шпинелях трехзарядные катионы занимают октаэдрические пустоты, Таблица 11.5 Окраска вещества и положение максимумов в спектрах поглощения
а двухзарядные — тетраэдрические. В «обращенных» шпинелях трехзарядные катионы расположены в тетраэдрических и октаэдрических полостях, а двухзарядные — в октаэдрических. Используя значения ЭСКП, можно рассчитать «энергии предпочтения к октаэдрической конфигурации» (ЭПОК), полагая, что ионы О2– в оксидах создают слабое кристаллическое поле. Проиллюстрируем расчет на шпинелях FеСr2O4 и Fе2Fе O4 (т. е. Fe3O4). В хромистом железняке FеСr2O4 ЭСКП для иона Fе2 (d 6) в октаэдрическом поле δ = 0,4Δo = 0,9Δt а ЭСКП в тетраэдрическом поле δ = 0,6Δt Для иона Fе2 ЭПОК = 0,3Δt. Для иона Cr3 (d 3) ЭСКП в октаэдрическом поле δ = 1,2Δo = 2,7Δt а ЭСКП в тетраэдрическом поле δ = 0,2Δt ЭПОК≈2,5Δt. Следовательно, в октаэдрическом окружении выгоднее находиться катиону Сr3, поэтому в FeCr2O4 структура нормальной шпинели. В шпинели Fе2Fе O4 ионы Fе2 (d 6, δ = 0,4Δo) стабилизируются в октаэдрических полостях сильнее, чем в тетраэдрических, а ионы Fе3 (d 5, δ = 0) дополнительной стабилизации не имеют. Поскольку ЭПОК для Fe2 больше, чем для Fe3, шпинель должна быть обращенной; это подтверждается экспериментально. Вопросы11.12. Определите число неспаренных электронов центрального иона и, используя теорию КП, предскажите магнитные свойства следующих октаэдрических комплексов: а) [Fе(Н2O)6]2; б) [Fе(CN)6]4–; в) [Сr(NO)(CN)5]3–; г) [Со(en)3]3; д) [Мn(CN)6]4–; е) [Со(NO2)6]4–; ж) [Fе(СN)6]3–; з) [Мn(CN)6]3–; и) [Сr(CN)6]6–; к) [Со(Н2O)2(CN)4]–. 11.13. Определите число неспаренных электронов в следующих ком- плексных ионах: a) [CoF6]3–; б) [Co(NH3)6]3; в) [Fe(H2О)6]3; г) [Сr(Н2O)6]2; д) [CoF6]3–; е) [Мn(Н2O)6]2; ж) [Мn(С2O4)3]3–. Используя теорию КП, предположите, какие из этих октаэдрических комплексов диамагнитны, а какие парамагнитны. 11.14. Объясните причину диамагнетизма гексацианокобальтат(III)иона и парамагнетизма гексафторокобальтат(III)-иона. 11.15. Используя теорию КП, объясните природу тетрагонального искажения оксида Mn3O4 (структурный тип шпинели). 11.16. Объясните, используя теорию КП плоскоквадратную геометрию комплекса [Ni(CN)4]2–. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
