|
|
Теория информационных систем. 13. Модели управления запасами
Цели
Возникновение теории управления запасами можно связать с работами Ф. Эджуорта и Ф. Харриса, появившимися в конце XIX — начале XX века, в которых исследовалась простая оптимизационная модель для определения экономичного размера партии поставки для складской системы с постоянным равномерным расходом и периодическим поступлением хранимого продукта.
Запасом называется любой ресурс, который хранится для удовлетворения будущих нужд. Примерами запасов могут стать полуфабрикаты, готовые изделия, материалы, различные товары, а также денежная наличность, находящаяся в хранилище.
Существуют причины, побуждающие фирмы создавать запасы:
1) дискретность поставок при непрерывном потреблении;
2) упущенная прибыль в случае отсутствия запаса;
3) случайные колебания:
А) спроса за период между поставками;
Б) объема поставок;
В) длительности интервала между поставками;
4) предполагаемые изменения конъюнктуры:
А) сезонность спроса;
Б) сезонность производства.
Существуют также причины, побуждающие предприятия стремиться к минимизации запасов на складах:
1) плата за хранение запаса;
2) физические потери при хранении;
3) моральный износ продукта.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь формулировать и использовать для экономического анализа следующие понятия:
• запас;
• заказ;
• издержки выполнения заказа (издержки заказа);
• издержки хранения;
• упущенная прибыль (издержки дефицита);
• срок выполнения заказа;
• точка восстановления.
Модели
Существует проблема классификации имеющихся в наличии запасов. Для решения этой задачи используется методика административного наблюдения. Цель ее заключается в определении той части запасов фирмы, которая требует наибольшего внимания со стороны отдела снабжения. Для этого каждый компонент запасов рассматривается по двум параметрам:
1) его доля в общем количестве запасов фирмы;
2) его доля в общей стоимости запасов.
Методика 20/80. В соответствии с этой методикой компоненты запаса, составляющие 20% его общего количества и 80% его общей стоимости, должны отслеживаться отделом снабжения более внимательно.
Методика АВС. В рамках этой методики запасы, имеющиеся в распоряжении предприятия, разделяются на три группы: А, В и С.
Группа А: 10% общего количества запасов и 65% их стоимости;
В: 25% общего количества запасов и 25% их стоимости;
С: 65% общего количества запасов и около 10% их стоимости.
Именно Наименьшая по объему и Наиболее ценная часть запасов может стать предметом особого контроля и математического моделирования.
Необходимо отметить, что классификация запасов может быть основана не только на показателях доли в общей стоимости и в общем количестве. Некоторые виды запасов могут быть причислены к более высокому классу на основании таких характеристик, как специфика поставок, качество и т. д. Преимущество методики деления запасов на классы заключается в том, что для каждого из них можно выбрать свой порядок контроля и управления.
Отметим некоторые моменты политики управления запасами, классификация которых проведена на основе АВС-анализа.
1. Запасы группы А требуют более внимательного и частого проведения инвентаризации; правильность учета запасов этой группы должна подтверждаться чаще.
2. Планирование и прогнозирование запасов группы А должно характеризоваться большей степенью точности, нежели планирование запасов групп В и С.
3. Для группы А нужно стараться создать страховой запас, чтобы избежать больших расходов, связанных с отсутствием запасов этой группы.
4. Методы и приемы управления запасами, рассмотренные далее, должны применяться прежде всего к группам А и В. Что касается запасов группы С, обычно момент возобновления заказа по ним определяют исходя из конкретных условий, а не на основе количественного метода, чтобы свести к минимуму расходы на их контроль.
Рассмотрим основные понятия теории управления запасами.
Издержки выполнения заказа (издержки заказа) — накладные расходы, связанные с оформлением заказа. В промышленном производстве такими издержками являются затраты на переналадку оборудования и подготовительные операции.
Издержки хранения — расходы, связанные с физическим содержанием товаров на складе, плюс возможные проценты на капитал, вложенный в запасы. Обычно они выражены в абсолютных единицах или в процентах от закупочной цены и связаны с определенным промежутком времени.
Упущенная прибыль (издержки дефицита) — издержки, связанные с неудовлетворенным спросом, возникающим из-за отсутствия продукта на складе.
Совокупные издержки за период представляют собой сумму издержек заказа, издержек хранения и упущенной прибыли. Иногда к ним прибавляются издержки на закупку товара.
Срок выполнения заказа — время с момента заказа до момента его выполнения.
Точка восстановления — уровень запаса, при котором делается новый заказ.
I. Детерминированные модели
1. Простейшая модель оптимального размера заказа.
Предположим, что:
1) темп спроса на товар известен и постоянен;
2) получение заказа мгновенно;
3) закупочная цена не зависит от размера заказа;
4) дефицит не допускается.
Исходные данные: темп спроса, издержки заказа, издержки хранения.
Результат: оптимальный размер заказа, время между заказами, количество заказов за фиксированный период времени, совокупные издержки.
Размер заказа является постоянным. Заказ выполняется мгновенно. Уровень запасов убывает с постоянной интенсивностью, пока не достигает нулевого значения. В этот момент времени делается и мгновенно выполняется заказ и уровень запаса восстанавливается до максимального значения. При этом Оптимальным решением задачибудет такой размер заказа, при котором минимизируются общие издержки за период, равные сумме издержек хранения и издержек заказа.
Динамика изменения количества продукта S на складе показана на рис. 1.
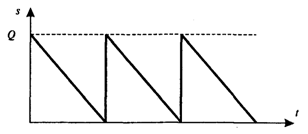
Рис. 1
Пусть Q — размер заказа;
Т — продолжительность периода планирования;
D, D — величина спроса за период планирования и в единицу времени соответственно;
К — издержки одного заказа;
Н, H — удельные издержки хранения за период и в единицу времени соответственно.
Тогда:
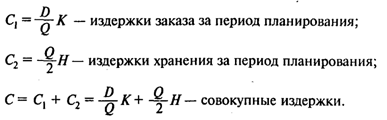
Кривые издержек заказа С1 издержек хранения С2 и совокупных издержек С показаны на рис. 2.
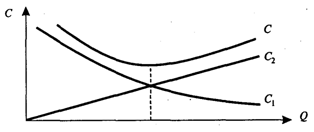
Рис.2
Определив минимум функции совокупных издержек, получаем:
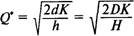 — оптимальный размер заказа; — оптимальный размер заказа;
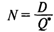 — оптимальное число заказов за период; — оптимальное число заказов за период;
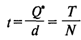 — время цикла (оптимальное время между заказами). — время цикла (оптимальное время между заказами).
Следует обратить внимание на то, что оптимальный размер заказа не зависит от цены продукта.
2. Модель оптимального размера заказа с фиксированным временем его выполнения.
Предположим, что:
1) темп спроса на товар известен и постоянен;
2) время выполнения заказа известно и постоянно;
3) закупочная цена не зависит от размера заказа;
4) дефицит не допускается.
Исходные данные: темп спроса, издержки заказа, издержки хранения, время выполнения заказа.
Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса, количество заказов за фиксированный период времени, совокупные издержки.
Размер заказа является постоянным. Время выполнения заказа постоянно. Уровень запасов убывает с постоянной интенсивностью, пока не достигает точки восстановления R. В этот момент делается заказ, который выполняется за время L. К моменту поступления заказа размер запаса на складе равен нулю. Оптимальным решением задачибудет такой размер заказа Q*, при котором минимизируются общие издержки за период, равные сумме издержек хранения и издержек заказа.
Динамика изменения количества продукта S на складе показана на рис. 3.
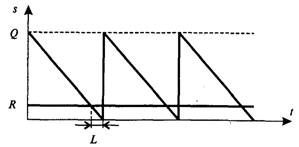
Рис.3
Пусть Q — размер заказа;
Т — продолжительность периода планирования;
D, D — величина спроса за период планирования и в единицу времени соответственно;
К — издержки одного заказа;
Н, H — удельные издержки хранения за период и в единицу времени соответственно;
L — время выполнения заказа. Тогда:
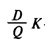 — издержки заказа за период планирования; — издержки заказа за период планирования;
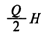 — издержки хранения за период планирования; — издержки хранения за период планирования;
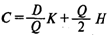 — совокупные издержки; — совокупные издержки;
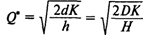 — оптимальный размер заказа; — оптимальный размер заказа;
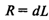 — точка восстановления запаса; — точка восстановления запаса;
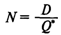 — оптимальное число заказов за период; — оптимальное число заказов за период;
 — время цикла (оптимальное время между заказами). — время цикла (оптимальное время между заказами).
Кривые издержек заказа С1, издержек хранения С2 и совокупных издержек С показаны на рис. 2.
3. Модель оптимального размера заказа с производством.
Предположим, что:
1) темп спроса на товар известен и постоянен;
2) темп производства товара известен и постоянен;
3) время выполнения заказа известно и постоянно;
4) закупочная цена не зависит от размера заказа;
5) дефицит не допускается.
Исходные данные: темп спроса, темп производства, издержки заказа, издержки хранения, время выполнения заказа.
Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса.
Фирма производит продукт самостоятельно, хранит его на складе и расходует с постоянным темпом. Если темп производства выше темпа спроса, то излишки продукта накапливаются на складе. Когда количество продукта на складе достигает максимального значения, производство прекращается и продукт расходуется со склада с постоянным темпом. Когда запас на складе достигает точки восстановления, производство возобновляется. При этом Оптимальным решением задачи будет такой размер заказа Q*, При котором минимизируются общие издержки за период, равные сумме издержек хранения и издержек на возобновление (запуск) производства.
Динамика изменения количества продукта S на складе показана на рис. 4, где tg a = Р – D, tg b = D.
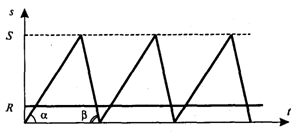
Рис.4
Пусть Q — размер заказа;
Р —темп производства;
Т — продолжительность периода планирования;
D, D — величина спроса за период планирования и в единицу времени соответственно;
К — фиксированные издержки на запуск производства;
Н, H — удельные издержки хранения за период и в единицу времени соответственно;
L — время, необходимое для запуска производства. Тогда:
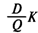 — издержки на запуск производства; — издержки на запуск производства;
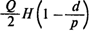 — издержки хранения; — издержки хранения;
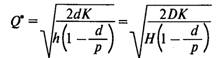 — оптимальный размер заказа; — оптимальный размер заказа;
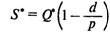 — оптимальный максимальный уровень запасов; — оптимальный максимальный уровень запасов;
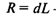 — точка восстановления; — точка восстановления;
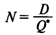 — оптимальное число заказов за период; — оптимальное число заказов за период;
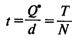 — время цикла (оптимальное время между заказами). — время цикла (оптимальное время между заказами).
В этой модели оптимальный размер заказа также не зависит от цены продукта.
4. Модель оптимального размера заказа с дефицитом.
Предположим, что:
1) темп спроса на товар известен и постоянен;
2) время выполнения заказа известно и постоянно;
3) закупочная цена не зависит от размера заказа.
Исходные данные: темп спроса, издержки заказа, издержки хранения, издержки дефицита.
Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса, совокупные издержки.
Размер заказа является постоянным. Уровень запасов убывает с постоянной интенсивностью. Допускается дефицит продукта. После получения заказа фирма компенсирует дефицит и восстанавливает запас продукта на складе. Заказ делается тогда, когда дефицит продукта на складе достигает оптимального размера. Оптимальным решением задачи будет такой размер заказа Q*, при котором минимизируются общие издержки за период, равные сумме издержек хранения, издержек заказа и издержек дефицита.
Динамика изменения количества продукта S на складе показана на рис.5.
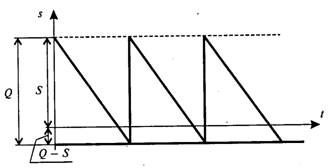
Рис.5
Пусть Q — размер заказа;
Т — продолжительность периода планирования;
D, d — величина спроса за период планирования и в единицу времени соответственно;
К — издержки одного заказа;
Н, h — удельные издержки хранения за период и в единицу времени соответственно;
В, B — упущенная прибыль, возникающая вследствие дефицита одной единицы продукта, за период и в единицу времени соответственно;
S — максимальный запас продукции;
L — время выполнения заказа.
Тогда:
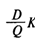 — издержки заказа за период планирования; — издержки заказа за период планирования;
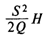 — издержки хранения за период планирования; — издержки хранения за период планирования;

5. Модель оптимального размера заказа с количественными скидками.
Предположим, что:
1) темп спроса на товар известен и постоянен;
2) время выполнения заказа известно и постоянно.
Исходные данные: темп спроса, издержки заказа, издержки хранения, цена товара, количественные скидки в случае закупки крупных партий товара.
Результат: оптимальный размер заказа, время между заказами, точка восстановления запаса, количество заказов за фиксированный период времени, совокупные издержки.
Пусть Q — размер заказа;
T — продолжительность периода планирования;
D, D —величина спроса за период планирования и в единицу времени соответственно;
К — издержки одного заказа;
Н, H — удельные издержки хранения за период и в единицу времени соответственно.
Предположим, что известны числа СI, АI, I = 1, ..., П, где СI — цена продукта при размере заказа Q в интервале AI–1 £ Q < аI. Будем считать, что A0 = 0 и An = +¥.
Тогда:

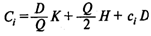
Оптимальный размер заказа определяется в результате решения П задач. Каждая из этих задач сводится к определению такого размера заказа Qi, I = 1,..., П, при котором функция совокупных (общих) издержек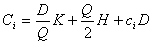 достигает минимума при ограничениях достигает минимума при ограничениях 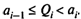
Решение исходной задачи определяется из условия
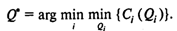
На рис. 6 изображены функции совокупных издержек для трех значений цен продукта. Значение цены C1 определено на интервале 0 £ Q < А1, цены С2 — на интервале A1 £ Q < А2, цены C3 — на интервале A2 £ Q < +¥.
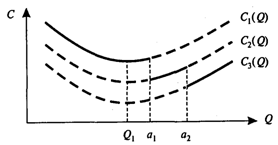
Рис. 6
Соответственно, функция общих издержек C1(Q) определена при значении цены С1 на интервале 0 £ Q < А1, функцияC2(Q) — при значении цены С2 на интервале A1 £ Q < А2, функция C3(Q) — При значении цены C3 на интервале A2 £ Q < +¥.
Минимальное значение функции C1(Q) в области ее допустимых значений достигается в точке Q1, функции C2(Q) — в точке А1, Функции C3(Q) — в точке А2.
Оптимальный размер заказа следует выбирать из величин Q1, A1 и A2 по формуле
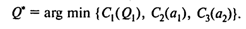
II. Стохастическая модель
6. Дискретная стохастическая модель оптимизации начального запаса.
Мы отказываемся от предположения о постоянстве и детерминированности величины спроса на товар и предполагаем известным распределение величины спроса.
Пусть S — размер запаса на начало периода планирования;
D — величина спроса за период планирования (целое число);
Н — удельные издержки хранения за период;
В — удельные издержки дефицита за период;
P(D)— вероятность того, что величина спроса за период планирования составит D.
Функция распределения величины спроса F(X) = Р (D < х) = 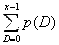 . .
В случае когда величина спроса за период планирования превышает размер запаса (D > S), возникает дефицит и соответствующие издержки дефицита. Если запас больше, чем величина спроса (S > D), то возникают издержки хранения. Математическое ожидание C1(S) величины издержек хранения за период планирования для размера начального запаса S можно оценить следующим образом:
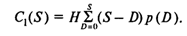
Математическое ожидание С2(S) величины издержек дефицита за период планирования для размера начального запаса S можно оценить следующим образом:
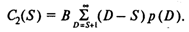
Математическое ожидание C(S) совокупных издержек в этом случае имеет вид
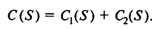
В стохастической модели Оптимальным является такой размер начального запаса S*, при котором математическое ожидание совокупных издержек C(S*) имеет минимальное значение, т. е. такой размер запаса S*,который удовлетворяет условию
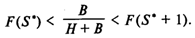
Если  и оптимальными являются как размер запаса S*, так и размер запасаS* + 1. и оптимальными являются как размер запаса S*, так и размер запасаS* + 1.
|
Тема 14 УПРАВЛЕНИЕ ЗАПАСАМИ И ЗАКУПКАМИ
Теоретические пояснения к решению задачи
Все широко применяемые в настоящее время логистические системы используют запасы. Следовательно, для каждого предприятия важной задачей является разработка оптимальной стратегии управления запасами. В качестве запасов можно рассматривать сырье, полуфабрикаты и готовую продукцию. Задача управления запасами напрямую связана с организацией процесса закупок, а также со сбытом готовой продукции. Методы и модели теории управления запасами позволяют определить оптимальные решения по управлению логистическими подсистемами снабжения запасов, и сбыта, обеспечить эффективную и согласованную работу этих подсистем.
Задача управления запасами в общем случае формулируется следующим образом: определить оптимальный размер запаса, размер, частоту и сроки поставки заказа, минимизирующие суммарные затраты. В затраты обычно входит стоимость закупки, доставки и хранения продукции.
Ниже будут рассмотрены различные модели или задачи управления запасами, соответствующие различным входным условиям и внутренним требованиям исследуемой системы Расчет моделей позволяет минимизировать затраты на закупку, доставку заказов и хранение запасов, то есть оптимизировать работу логистической системы предприятия.
Можно выделить следующие основные характеристики моделей управления запасами:
1. Спрос. Может быть детерминированным (определенным) или случайным.
2. Размер заказа. Запасы пополняются с помощью заказов. В общем случае размер заказа зависит от величины запаса в момент подачи заявки на заказ.
3. Точка заказа или уровень повторного заказа. Размер запаса, при котором подается заявка на заказ, называется точкой заказа.
4. Время доставки заказа. Это время, прошедшее от момента заказа в точке заказа до момента поставки заказа. Может быть детерминированным или случайным.
5. Стоимость закупки продукции.
6. Стоимость доставки заказа. Учитывает затраты на транспортное средство, заработную плату водителей, налоговые сборы при импортировании продукции или оплату фирмы-посредника, занимающейся перевозками.
7. Стоимость хранения запасов. Является суммарной величиной, учитывающей затраты на непосредственное содержание складов, оплату персонала, работающего на складе, затраты на электроэнергию, а также убытки, связанные с замораживанием капитала в запасах, порчу и утерю хранимых материальных единиц.
9. Штраф за дефицит. Убытки, связанные с отсутствием требуемой продукции, называются штрафом за дефицит.
Корректное определение последних трех величин во многом определяет верность решения при расчете моделей управления запасами.
10. Номенклатура запасов. Запас может однопродуктовым и многопродуктовым.
10. Структура складской системы. Склад может быть одиночным, может рассматриваться иерархическая система складов с различными периодами пополнения и возможностями обмена продукцией между складами.
Процесс управления запасами - циклический (рис. 13). Снижение уровня запасов определяется спросом В точке заказа для пополнения запасов делается заказ. По истечении времени доставки заказ будет получен и уровень запасов возрастает.
При рассмотрении модель управления запасами без дефицита в качестве ограничений модели рассматриваются постоянный спрос, равномерность расходования запаса, отсутствие дефицита (рис. 14). Эти условия не всегда исполнимы в реальности.
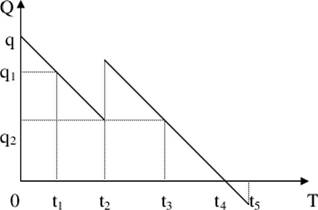
Рис. 13. Общая схема управления запасами на предприятии
Условные обозначения:
Q - количество единиц продукции; Т - период хранения запасов; t1 - момент времени, в который делается заказ; t2 - момент времени получения заказа; t2 - t1 - время доставки; t5 - t4- время, когда запас отсутствует; q - размер запаса; q1, q2 - точки заказа.
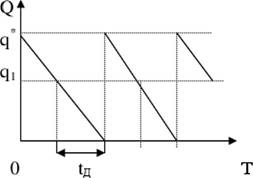
Рис. 14. Схема управления запасами без дефицита
В этой модели оптимальные размеры заказа и запаса совпадают.
Условные обозначения:
Q - количество единиц продукции; Т - период хранения запасов; D - спрос; q - размер заказа; q* - экономичный размер заказа; q1 - точка заказа; tд - время доставки заказа; n - число заказов за период Т; С1 - стоимость доставки одного заказа; С2 - стоимость хранения единицы продукции в единицу времени; Сд - стоимость доставки заказов за период Т; Сх - стоимость хранения запасов за период Т; С - стоимость логистической системы за период Т.
Оптимальный размер запаса и заказа определяется по формуле Вильсона или формуле экономичного размера заказа (EOQ - Economic Optimal Quantity). Для экономичного размера заказа EOQ стоимость доставки заказов равна стоимости хранения запасов (рис. 15).
При небольшом размере определяющей величиной является стоимость его доставки. Это означает, что заказы доставляются часто и небольшой величины. При увеличении размера заказа определяющей становится стоимость хранения запаса. Такие запасы поставляются редко и значительно увеличивают размер хранящейся на складе продукции.
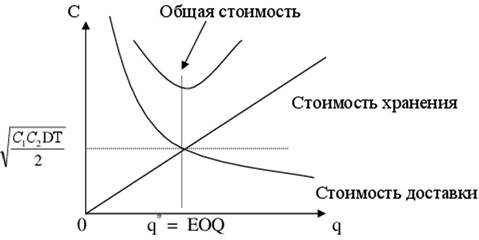
Рис. 15. График стоимости логистической системы
Расчет основных показателей модели управления запасами без дефицита:
1. Экономичный размер заказа:
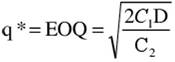 (1) (1)
2. Число заказов за время Т:
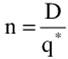 (2) (2)
3. Интервал времени между заказами:
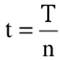 (3) (3)
4. Точка заказа или уровень повторного заказа:
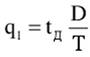 (4), (4),
где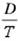 - потребление в единицу времени. - потребление в единицу времени.
5. Минимальная стоимость логистической системы управления запасами:
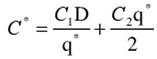 (5) (5)
При оптовых закупках стоимость логистической системы зависит от размера заказа. На большие заказы обычно предоставляются скидки. Заказы на крупные партии ведут к увеличению стоимости хранения запасов, которая может компенсироваться снижением закупочной цены.
Стоимость определяется формулой:
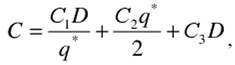 (6) (6)
где С3 - закупочная цена единицы продукции. Уровень заказа, начиная с которого устанавливается скидка, называется уровнем q0, нарушающим цену.
Если экономичный размер заказа не включается в интервал предоставления скидок, то следует пересчитать оптимальный размер заказа, соответствующий минимальной стоимости.
Пример решения задачи.
Магазин закупает товар в упаковках по 2 у.е. за одну упаковку. Спрос на товар составляет 500 упаковок в год. Величина спроса равномерно распределяется в течение года. Доставка одного заказа равна 10 у.е., время доставки составляет 12 рабочих дней. Предполагается, что в году 300 рабочих дней. Среднегодовая стоимость хранения одной упаковки оценивается в 20% от ее закупочной цены. Поставщик предоставляет следующие скидки на закупочные цены:
Следует ли администрации магазина воспользоваться одной из скидок?
Размер заказа, упаковок
|
Скидка, %
|
Цена за упаковку, у.е
|
Стоимость
хранения
|
0-199
|
0
|
2
|
|
200-499
|
10
|
1,8
|
|
500 и более
|
20
|
1,6
|
|
D - 500 (ед); Т - 300 (дн); С1 - 10 (у.е.); tд - 12 (дн.).
1. Расчет показателей логистической системы без учета скидок.
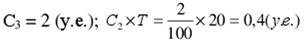
Экономичный размер заказа
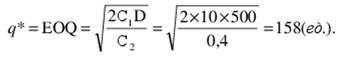
Для определения минимальной стоимости подставим в формулу (6) значения q*. Получим
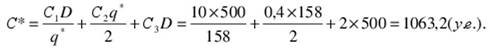
2. Пересчет показателей логистической системы для скидки 10%
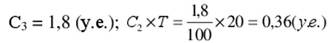
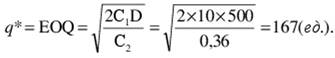
167 < 200, следовательно, расчет стоимости следует произвести для нижней границы предоставления скидки, равной 200.
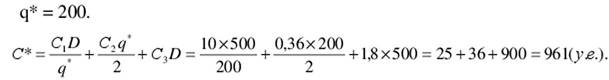
3. Пересчет показателей для скидки 20%.
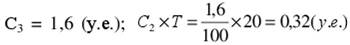
(среднегодовая стоимость хранения одной упаковки).
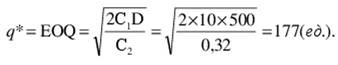
177 < 500. Минимально возможная стоимость будет получена для
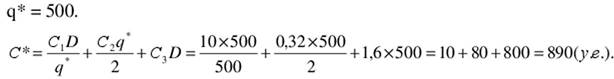
Минимальная стоимость логистической системы с учетом закупочной цены соответствует оптовой закупке в размере 500 единиц один раз в год.
Задача для самостоятельного решения
Предприятие-посредник, занимающееся продажей автомобилей, реализует в среднем 150 автомобилей в год. Стоимость доставки каждого заказа от производителя оценивается в 1500 у.е., а среднегодовая стоимость хранения одного автомобиля составляет 30% от закупочной цены. Если размер заказа меньше, чем 50 автомобилей, то цена закупки составляет 6000 у.е. Для заказов, имеющих размер от 50 до 99 автомашин, предоставляется скидка на закупочную цену в 3%, заказам при покупке 100 и более автомобилей - скидка, равная 5%. Определить оптимальный размер заказа и стоимость логистической системы.
|
|
|
|
 Скачать 269.01 Kb.
Скачать 269.01 Kb.