Учебник надежности. 2 Классические методы расчета надежности

• Название: 2 Классические методы расчета надежности
• Анкор: Учебник надежности
• Дата: 03.08.2022
• Размер: 0.88 Mb.
• Имя файла: Glava2.doc
• Тип: Документы; #639700
• страница: 2 из 3

Рис. 2.10. Пример образования соединения графа

Вес j-го соединения

,

где  – число независимых замкнутых контуров, образующих соединение, R(S_j) – множество независимых замкнутых контуров, образующих соединение.

Определитель графа
,
где S — множество всех возможных соединений графа.

Теперь рассмотрим методику расчета показателей надежности топологическим методом в установившемся режиме, где топологические коэффициенты С_i для каждой x_i вершины графа определяются непосредственно по графу, а затем вычисляется нужный показатель по ниже приведенным топологическим формулам.

Для определения коэффициента С_i необходимо:

– выбрать начальную вершину графа x_q отдельно для определения каждого из коэффициентов С_i ( ); начальная вершина может быть выбрана произвольно, однако выбор влияет на объем вычислений, поэтому ее надо выбирать так, чтобы были длинные прямые пути;

– построить множество К прямых путей из начальной вершины x_q в вершину x_i, для которой определяется коэффициент;

– для каждого k-го прямого пути построить множество замкнутых контуров подграфа G{X_k} и образовать возможные комбинации независимых замкнутых контуров (множество соединений S), где G{X_k} – подграф графа G{X, W}, образованный удалением множества вершин, входящих в k-й путь и прилегающих к нему дуг;

– записать коэффициенты C_i по найденным составляющим по формуле

гдe К – множество прямых путей из произвольно выбранной вершины х_q в х_i; Х_к - множество вершин, входящих в k-ый прямой путь.

Используя топологические коэффициенты, основные показатели надежности установившегося режима можно записать:

– вероятность нахождения системы в i-м состоянии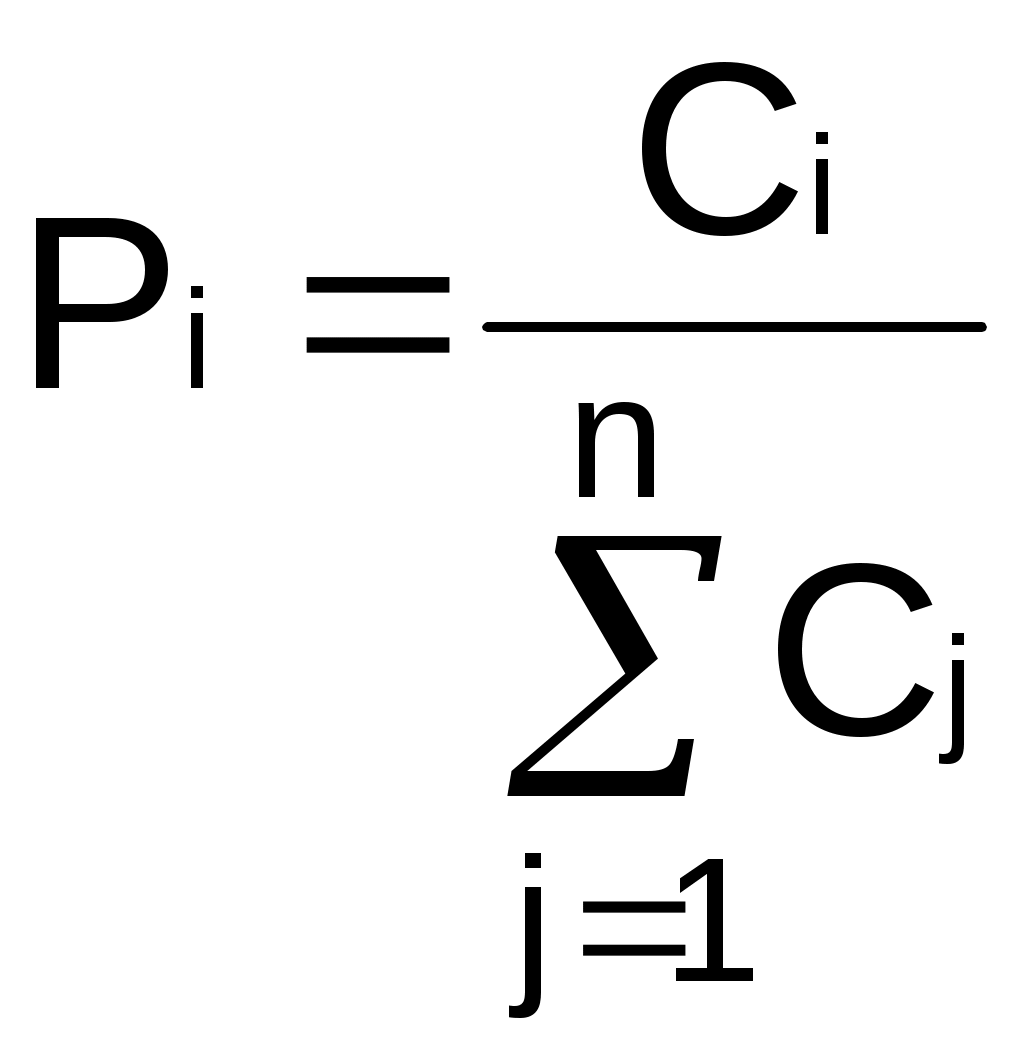

,

где n – число вершин графа;
– коэффициент готовности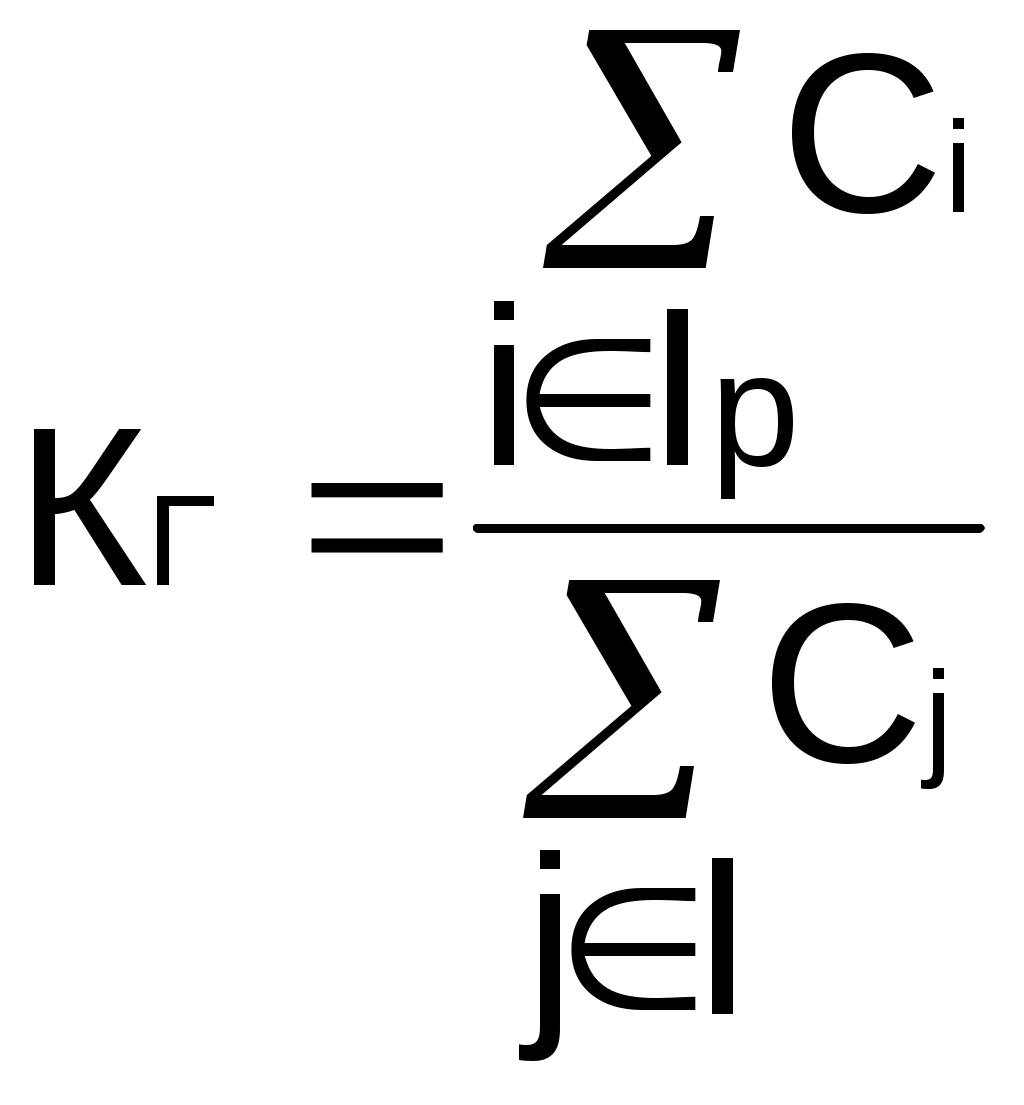

,

где I_p – множество индексов работоспособных состояний системы;
– коэффициент простоя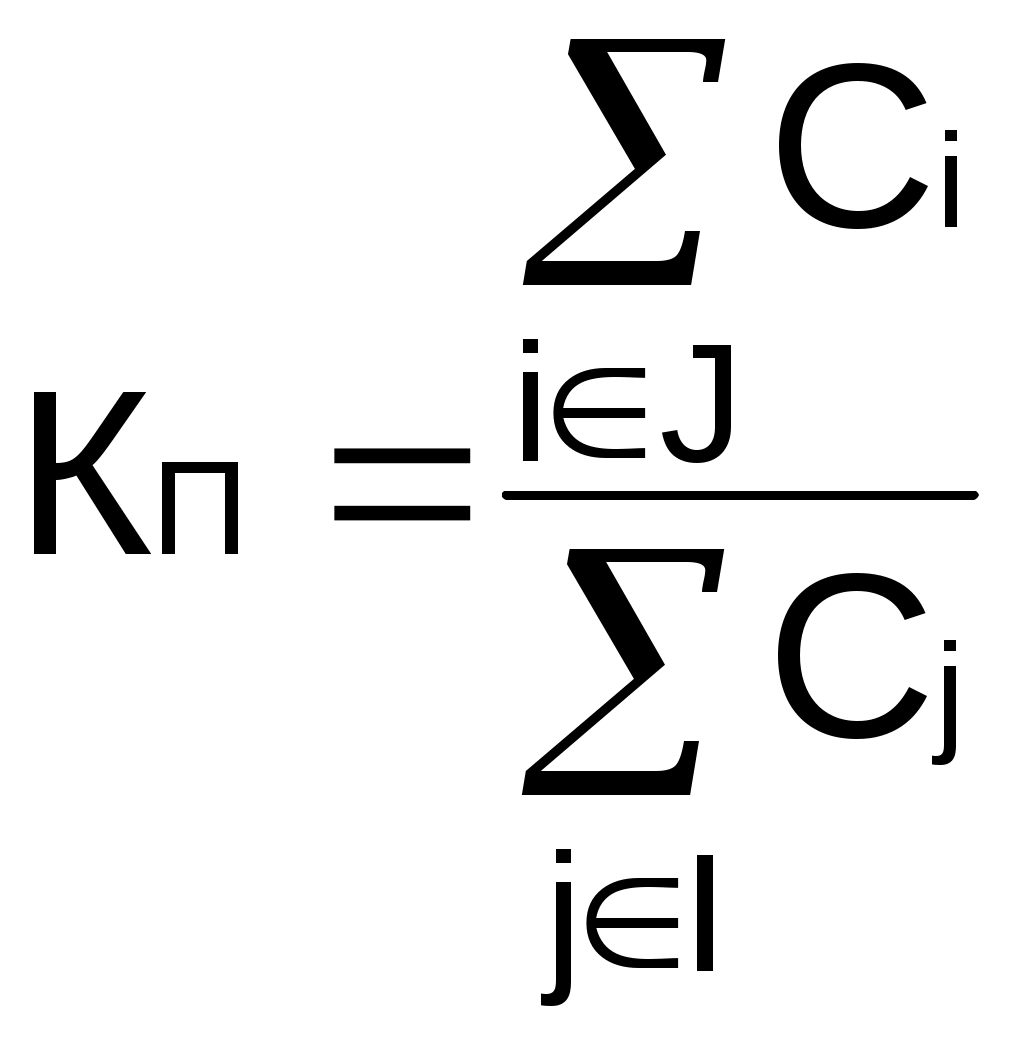

,

где J – множество индексов неработоспособных состояний системы;
– среднюю наработку на отказ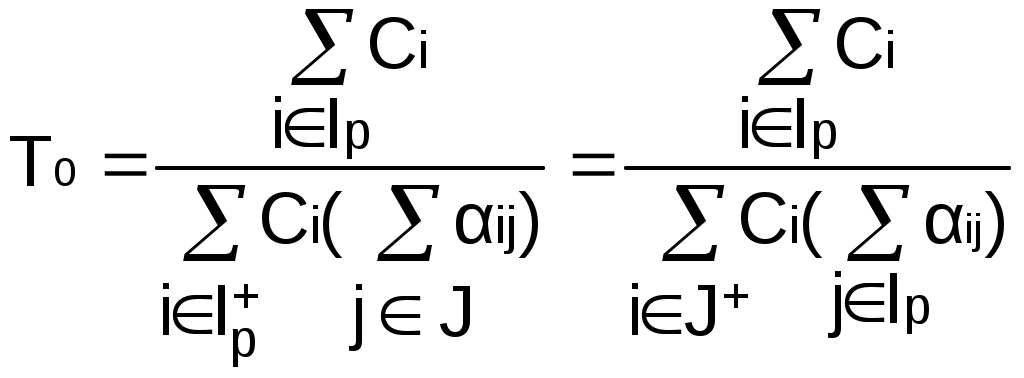

,

где – подмножество индексов граничных состояний из X_р, из которых в неработоспособное состояние можно попасть за один переход;

– среднее время восстановления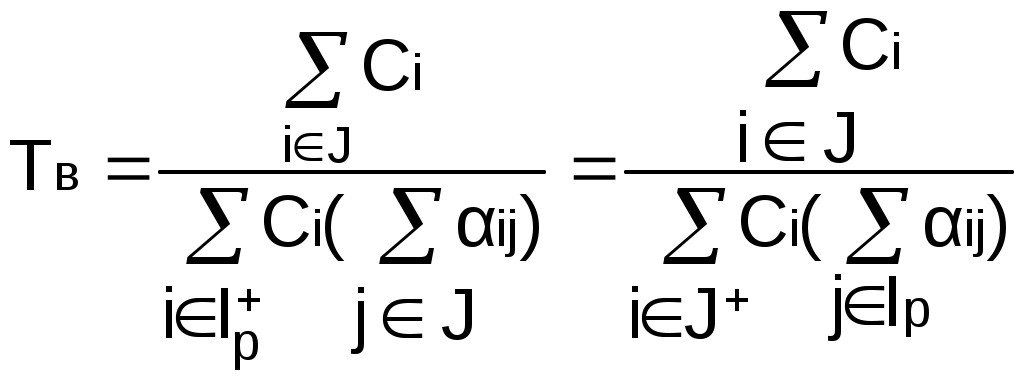

,

где J⁺ – подмножество индексов граничных состояний из , из которых в работоспособное состояние можно попасть за один переход.

Основные положения топологического метода могут быть применены для определения показателей надежности неустановившегося режима с использованием преобразований Лапласа.

Пример решения задачи

Имеется ИС, которая состоит из 2-х серверов. При работоспособности одного из серверов система работоспособна, так как каждый сервер может выполнять все функции.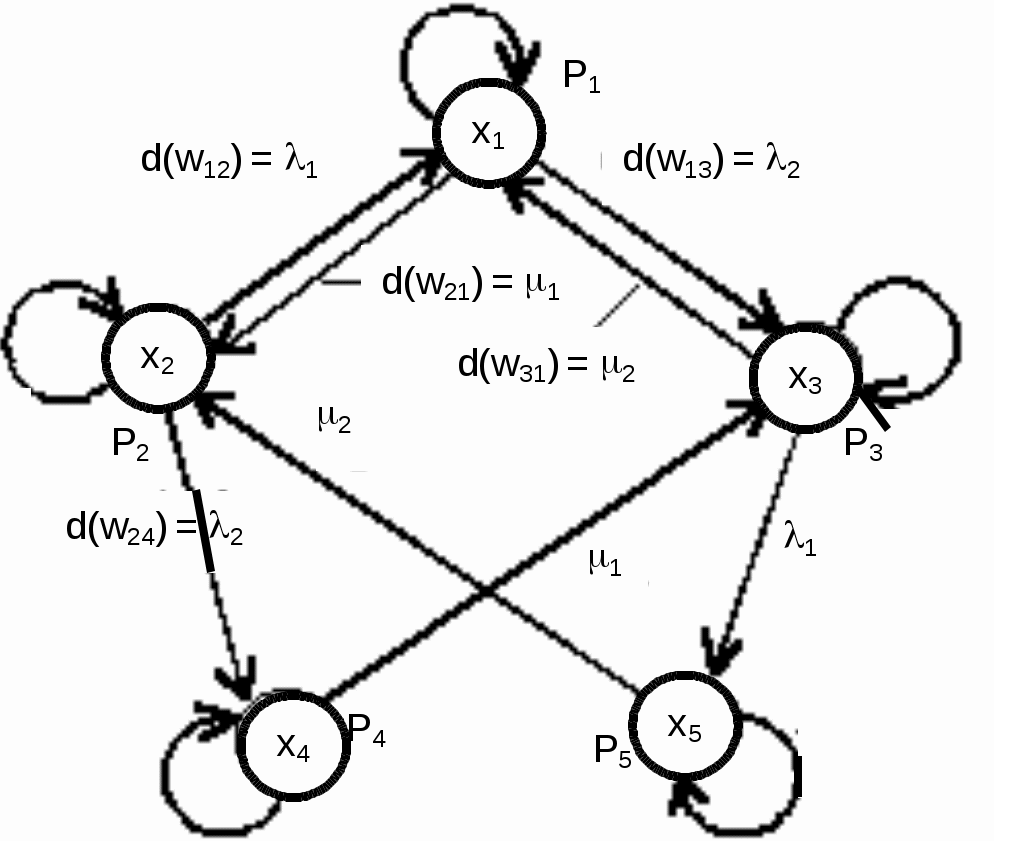







Рис. 2.11. Вероятностный граф состояний

Для обслуживания серверов существует одна бригада, ремонтирующая одновременно только один сервер, который отказал первым.

Необходимо определить топологическим методом показатели надежности.

Решение

Работоспособные состояния: x₁ – оба сервера в работоспособном состоянии; x₂ – отказ 1-го сервера и его восстановление, 2-й в работоспособном состоянии; x₃ – отказ 2-го сервера и его восстановление, 1-й в работоспособном состоянии.

Неработоспособные состояния: x₄ – при восстанавливающемся 1‑м сервере, отказал и 2-й; x₅ – при восстанавливающемся 2-м сервере, отказал 1-й сервер (рис. 2.11).

Вычисляем топологические коэффициенты. Для нахождения коэффициента C₁ в качестве начальной выбираем вершину x₅.
С₁=₅₂₂₄₄₃₃₁ + ₅₂₂₁(-1)^=2d(w₃₃)d(w₄₄) = ₅₂₂₁[-(₃₅+₃₁)]

(-₄₃) + ₅₂₂₄₄₃₃₁ = m₂m₁²(₁+m₂) + m₂²₂m₁ =

= m₂m₁(m₁₁ + m₁m₂ +m₂₂).
Для нахождения коэффициента C₂ в качестве начальной выбираем вершину x₄.

С₂=₄₃₃₅₅₂(-1)^=1d(w₁₁) + ₄₃₃₁₁₂(-1)^=1d(w₅₅) =

m₁₁m₂(₁ + ₂ ) + m₁m₂²₁ = m₁m₂(²₁+ ₁₂+ ₁ m₂),
С₃= m₁m₂(²₂+ ₁₂+ ₂ m₁),
С₄= ₁₂m₂(₁+ m₂ + ₂),
С₅= ₁₂m₁(₂+ m₁ + ₁).
Теперь можно определить искомые показатели надежности.

,
,
,
,
.

2.3. Логико-вероятностный метод расчета надежности
Метод основан на математическом аппарате алгебры логики. Расчет надежности системы управления предполагает определение связи между сложным событием (отказ системы) и событиями, от которых оно зависит (отказы элементов системы). Следовательно, расчеты на надежность основаны на проведении операций с событиями и высказываниями, в качестве которых принимаются утверждения о работоспособности или отказе элемента (системы). Каждый элемент системы представляется логической переменной, принимающей значение 1 или 0.

События и высказывания при помощи операций дизъюнкции, конъюнкции и отрицания объединяются в логические уравнения, соответствующие условию работоспособности системы. Составляется логическая функция работоспособности. Расчет, основанный на непосредственном использовании логических уравнений, называется логико-вероятностным и выполняется в семь этапов:

1. Словесная формулировка условий работоспособности объекта. Описывается зависимость работоспособности информационной системы от состояния ее отдельных элементов.

2. Составление логической функции работоспособности. Представляет собой логическое уравнение, соответствующее условию работоспособности системы управления

, (2.2)
которое выражено в дизъюнктивной форме, например:
,

где x_i – условие работоспособности i-го элемента Fл; X_i = 1 – работоспособное состояние, X_i = 0 – неработоспособное состояние.

3. Приведение логической функции работоспособности F_Л к ортогональной бесповторной форме F_ЛО. Сложную логическую функцию работоспособности необходимо привести к ортогональной бесповторной форме.

Функция вида (2.2) называется ортогональной, если все ее члены D_i попарно ортогональны (то есть, их произведение равно нулю), и бесповторной, если каждый ее член D_i состоит из букв х_i, с разными номерами (то есть отсутствуют повторяющиеся аргументы), например: произведение элементарных конъюнкций х₁, х₂, x₄ и х₃, x₂ равно нулю, так как одна из них содержит x₂, а другая – x₂, следовательно, они ортогональны; D₁ = x₁x₂x₂, где x₂ и x₂ имеют один и тот же номер, поэтому член D₁ не является бесповторным.
– ортогональная бесповторная форма;
– ортогональная, но не бесповторная форма.

Функцию F_л можно преобразовать к ортогональной бесповторной форме F_ло, используя законы и правила преобразования сложных высказываний. При расчетах наиболее употребительны правила:

1. 
   x₁x₂ = x₂x₁;
   
2. 
   ;
   
3. 
   ;
   
4. 
   ;
   
5. 
   ;
   
6. 
   x₁1 = 1;
   
7. 
   ;
   
8. 
   ;
   
9. 
   .
   

4. Арифметизация F_ло. По найденной ортогональной бесповторной логической функции работоспособности F_ЛО определяется арифметическая функция F_a (2.3).



(2.3)

где A_i – арифметическая форма членов D_i функции F_ло.
Арифметизация членов D_i, в общем виде содержащих операции дизъюнкции, конъюнкции и отрицания, осуществляется заменой логических операций арифметическими по правилам:

;

;

.

5. Определение вероятности безотказной работы системы.
Вероятность безотказной работы системы устанавливается как вероятность истинности логической функции работоспособности, представленной в ортогональной бесповторной форме, и вычисляется как сумма вероятностей истинности всех ортогональных членов этой функции алгебры логики. Все события (высказывания) заменяются их вероятностями (вероятностями безотказной работы соответствующих элементов).



6. Вычисление требуемых показателей надежности системы управления по найденному показателю P_c(t):

• 
  вероятность безотказной работы P_c(t);
  
• 
  вероятность отказа Q_c(t) = 1 – P_c(t);
  
• 
  интенсивность отказов ;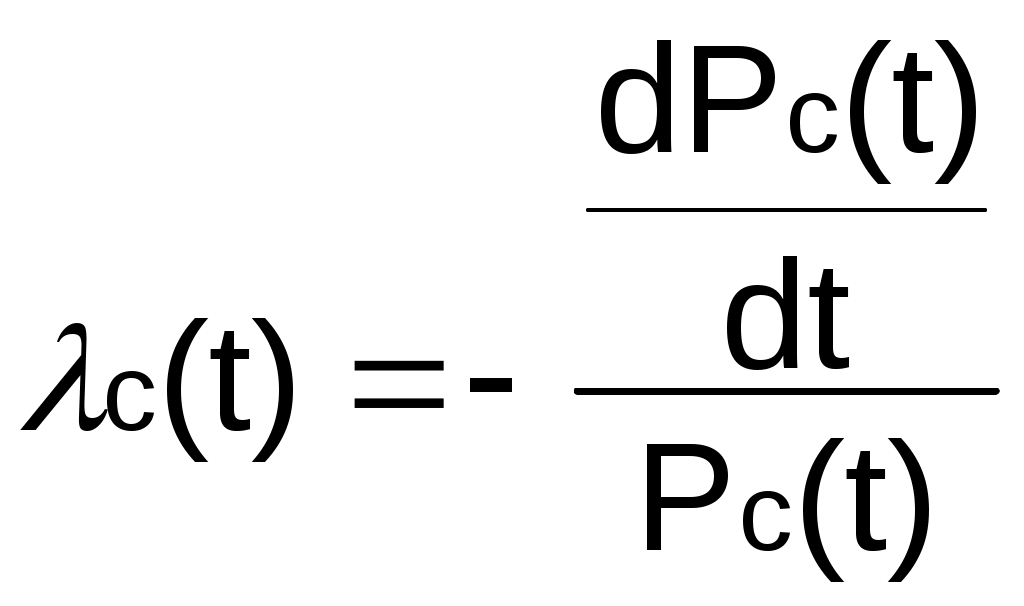
  
• 
  средняя наработка до отказа ;
  

7. Анализ соответствия полученных показателей надежности заданным техническим требованиям системы.

Допущения, принимаемые при логико-вероятностном методе: для элементов системы возможны только два состояния; метод применим для невосстанавливаемых систем; отказы элементов системы должны быть независимы.

Пример решения задачи

Имеется 2 автоматизированных рабочих места, между которыми есть 5 каналов связи, соединенных в виде мостиковой схемы. Определить вероятность безотказной работы каналов связи. Найти вероятность безотказной работы ИС, имеющей мостиковую структуру (рис. 2.4), если известны вероятности безотказной работы каждого элемента P₁= P₂=...= P₅= 0,9.

Решение

ИС будет работоспособна, если в работоспособном состоянии находятся каналы:

• 
  1,2,3,4,5;
  
• 
  1,2,3,4;
  
• 
  1,5,4;
  
• 
  2,5,3;
  
• 
  1,3;
  
• 
  2,4.
  

Составление логической функции работоспособности.



3. Приведение F_л к ортогональной бесповторной форме F_лo.

Применяя формулу (5) вышеприведенных правил (см. 3-й этап методики расчета), получаем:



Приводим к бесповторному виду, раскладывая согласно формуле (9) правил преобразования, функцию F_Л:

;

;

4. Арифметизация F_лo с целью нахождения F_а.

F_a = x₅[(x₃ + x₄ – x₃x₄)(x₁ + x₂ – x₁x₂)] +

+ (1 – x₅)(x₁x₃ + x₂x₄ – x₁x₃x₂x₄).

5. Вычисляем вероятность безотказной работы. Поскольку вероятности безотказной работы каналов не зависят от времени и равны по величине 0,9, вероятность безотказной работы ИС Р_с(t) определится как

P_c = P₅[(P₃ + P₄ – P₃  P₄)(P₁ + P₂ – P₁  P₂)] +

+ (1 – P₅)(P₁  P₃ + P₂  P₄ – P₁P₂P₃P₄).

Так как P_i= 0,9 для , то P_c = 0,978.

2.4. Структурный метод оценки надежности
Метод предназначен для оценки надежности человека-оператора в системах управления. С увеличением степени автоматизации роль человека как звена в системе управления постоянно возрастает, так как он переходит на более высокие уровни управления. Отказ человека-оператора в системе управления современным технологическим процессом приводит к значительным потерям.

Первые работы в области оценки надежности человека как звена в системе управления появились в СССР в 1964 – 1965 гг. Попытки первых исследователей перенести идеи и методы классической теории надежности на новый объект исследования – на человека – не увенчались успехом. Так, оказалось, что человеку свойственен принципиально новый тип отказа — ошибка в деятельности (временный неустойчивый отказ), а математические модели в рамках теории надежности технических систем этот тип отказа не учитывают.

Оценку надежности человека-оператора можно реализовать структурным методом[2]. В его основе лежит формализация деятельности человека-оператора в процессе решения в виде последовательной структуры. Структура – специальная логическая цепь, отображающая процесс функционирования системы человек-техника с количественными характеристиками единиц деятельности. Каждое звено имеет свои показатели надежности, которые потом используются в расчете надежности всей системы.

Деятельность человека последовательно представляется состоящей из операционных, функциональных и программных единиц.

Низший уровень рассмотрения деятельности человека-оператора – уровень операционных единиц.

Операционная единица – отдельный психофизиологический акт – является наименьшей единицей, до которой расчленяется деятельность человека-оператора, например, поворот ключа, нажатие кнопки и т. д.

Функциональная единица – группа операционных единиц, объединенных в структуре деятельности человека, в технологическом или смысловом отношении. Это специальные функциональные операции (блоки операций), подразделяемые на основные и вспомогательные функциональные единицы.

Основные единицы – единицы (блоки), в результате деятельности которых происходит достижение цели. К ним относят рабочий блок, блок задержки, блок принятия решений.

Вспомогательные блоки вводятся в структуру деятельности для увеличения безошибочности выполнения операций. При идеальной работе человека-оператора они не нужны (блок контроля ошибок, блок диагностического контроля).

Программная единица – совокупность функциональных единиц, объединенных в законченные блоки (программы), например, пуск насоса, подача топлива и т. д.

Рассмотрим показатели надежности функциональных единиц (функционально-программные надежности и функционально-временной надежности).

К основным блокам функциональных единиц относятся блоки, при невыполнении или ошибочном выполнении хотя бы одного из которых цель не будет достигнута. Основные блоки – рабочий блок, блок решения, блок задержки.

Рабочие блоки – блоки операций, в результате выполнения которых обеспечивается достижение цели (рис. 2.12).