синтез пид регулятора. прпарпр. 2. Разработка системы автоматического управления
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
2. Разработка системы автоматического управления 2.1. Описание объекта управления и оценка его динамических характеристик Объект управления (ОУ) представляет собой электромеханическую систему, состоящую из электродвигателя (ЭД) постоянного тока независимого возбуждения, силового пpеобpазователя (СП) напряжения и механизма с жесткой безpедуктоpной связью между электродвигателем и рабочим органом (РО). Предполагается наличие измерителей (датчиков) напряжения (ИН), тока (ИТ) и скорости (ИС), последний из которых содержит фильтрующий элемент (Ф) 1-го порядка. Функциональная схема объекта управления представлена на рис. 2.1.  Рис. 2.1. Функциональная схема объекта управления Исходные данные объекта управления. 1. Максимальная угловая скорость ЭД: Ωм = 314 150 рад/с. 2. Максимальный момент нагрузки: Mc = 8.39 8.8 Н∙м. 3. Суммарный момент инерции механической части (ЭД и РО): J = 0.1 0.08 кг∙м2. 4. Номинальное напряжение ЭД: Uн = 220 В. 5. Активное сопротивление якорной цепи: Ra = 0.81 4.66 Ом. 6. Индуктивность якорной цепи: La = 0.015 0.046 Гн. 7. Конструктивная постоянная ЭД: C = 0.67 1.21 Вб. 8. Номинальный ток ЭД: Iн = 13 А. 9. Максимальный ток ЭД: Iм = 3∙Iн. 10. Постоянная времени СП: Tсп = 0.0033 c при P > 2 3 кВт 11. Коэффициенты передачи а). датчика напряжения: Kдн = 0.05; б). датчика тока: Kдт = 0.5 В/А; в). датчика скорости: Kдс = 0.05 В∙с. 12. Постоянная времени фильтра ИС: Tф = 0.001 с. Технические требования к системе автоматического управления (САУ). 1. Максимально допустимая статическая ошибка стабилизации скорости: Δм = 0.5%(Ω = Ωм). 2. Полоса пропускания: 30 Гц для ЭМС с тиpистоpными 3-фазными СП (P > 2 кВт); 3. Время восстановления скорости при ступенчатом изменении момента нагрузки от нулевого до максимального значения (время возврата скорости к значению, равному 3∙Δм): Tв ≤ 1с. 4. Пеpеpегулиpование скорости: σ ≤ 20%. 2.1.1. Математическое описание ОУ в соотношениях «входа-выхода» (передаточных функциях) Для того чтобы исследовать автоматическую систему управления (АСУ), необходимо располагать её математическим описанием, характеризующим зависимости координат системы от внешних воздействий и друг от друга. Наиболее распространёнными способами математического описания, используемыми при проектировании и исследовании АСУ, являются дифференциальные уравнения, структурные схемы, представляющие графическую интерпретацию дифференциальных уравнений, векторно-матричное описание. Исходные дифференциальные уравнения объекта управления: 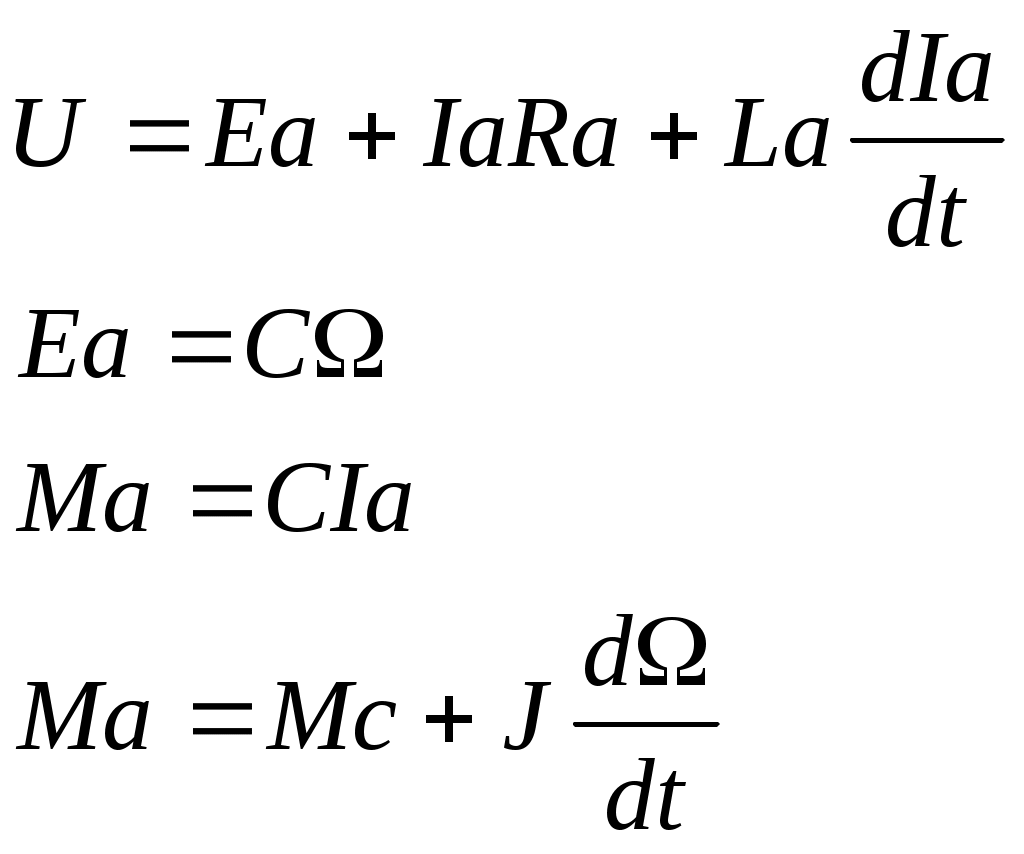 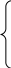 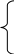 или или 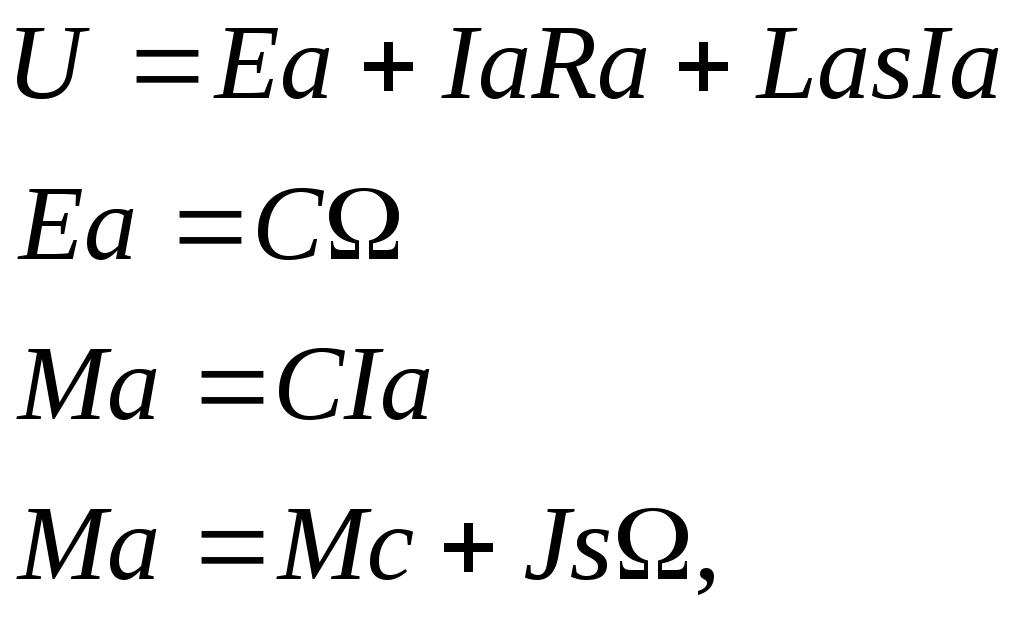 где U – номинальное напряжение двигателя, Ia – номинальный ток двигателя, Ra – активное сопротивление якорной цепи, La – индуктивность якорной цепи, С - конструктивная постоянная электродвигателя, Ω – скорость двигателя, Ma – движущий момент двигателя, Mc – максимальный момент нагрузки, J – момент инерции двигателя. Для удобства построения структурной схемы ОУ дифференциальные уравнения переписываются в следующем виде: 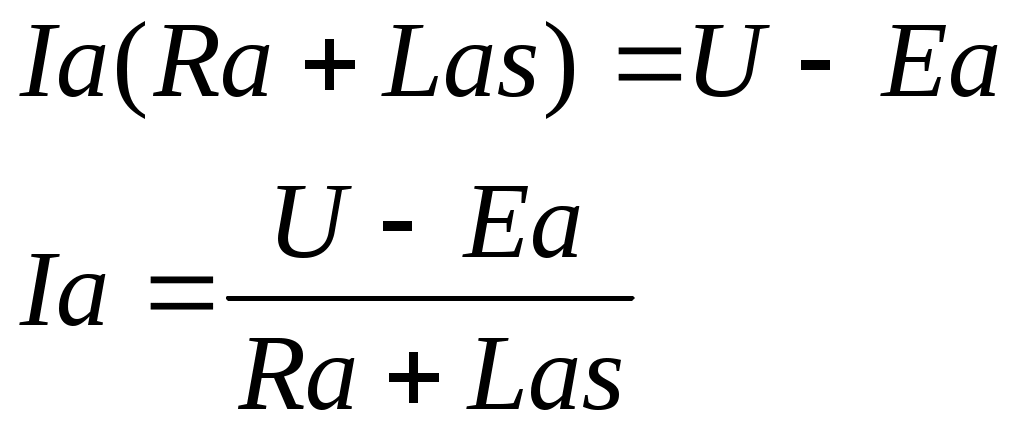  Силовой преобразователь представляется апериодическим звеном 1-го порядка с постоянной времени Tсп и коэффициентом передачи равным: где U = (0 – Uн) = (0 – 220) В, Uу = (0 – 10) В. Следовательно Структурная схема ОУ приведена на рис. 2.2. 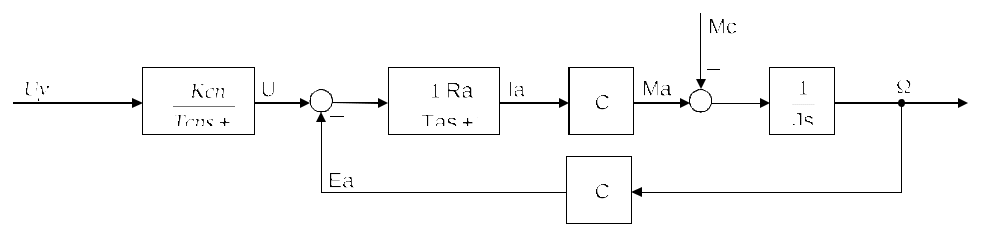 Рис. 2.2. Структурная схема объекта управления Рис. 2.2. Структурная схема объекта управленияПередаточная функция ОУ по управляющему воздействию Uу определяется по правилу Мейсона, которое применимо для систем любой сложности, т.к. не требует структурных преобразований и является универсальным:  Передаточная функция ОУ по возмущающему воздействию Mc: 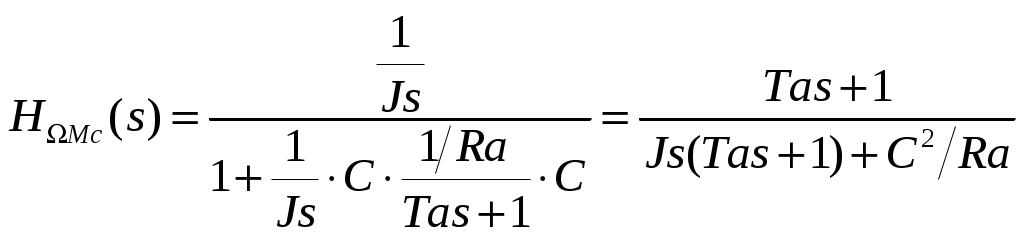 2.1.2. Оценка динамических характеристик ОУ корневыми, частотными и временными методами анализа Нули (корни числителя) и полюсы (корни знаменателя) передаточных функций ОУ. Передаточная функция по управляющему воздействию Uу: Полюсы 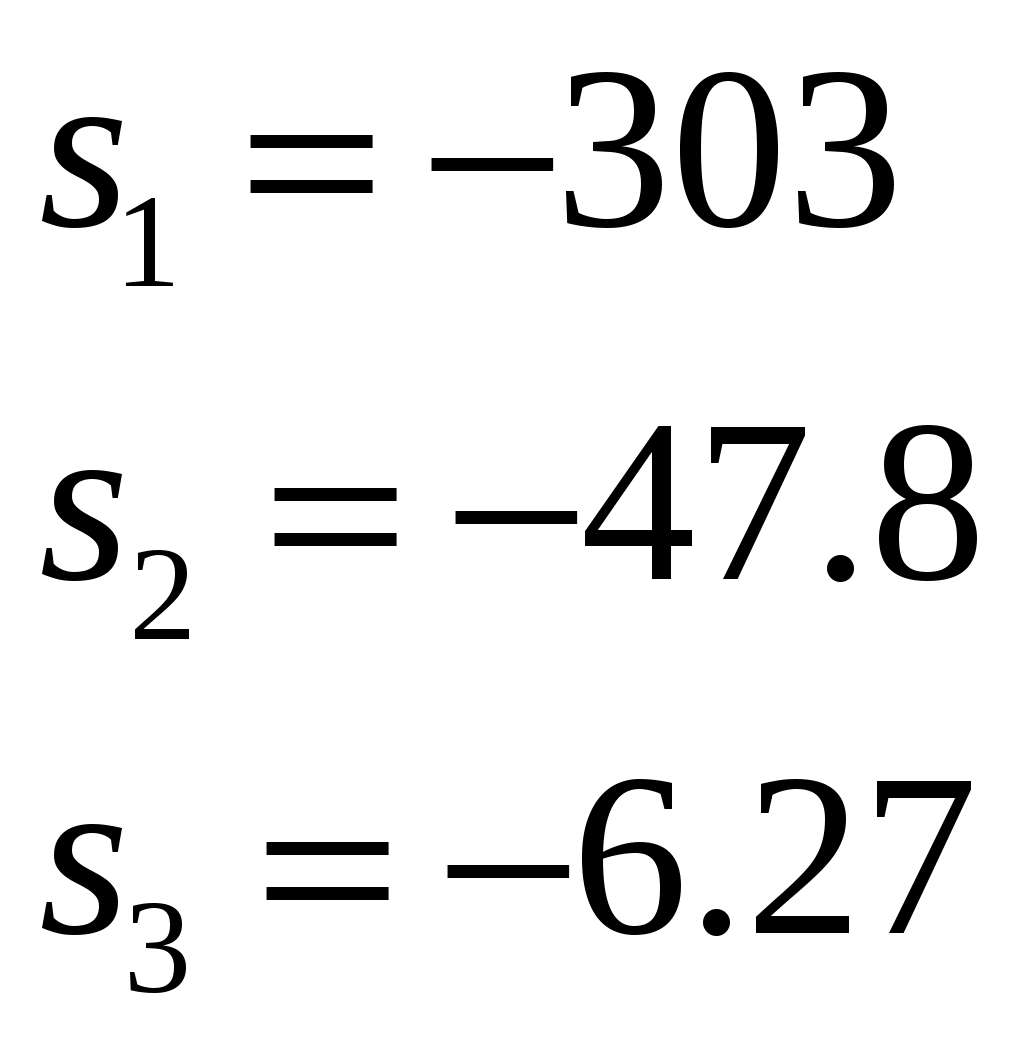 Передаточная функция по возмущающему воздействию Mc: Нули Полюсы Корневые показатели качества системы автоматического управления (САУ) приведены ниже. Среднегеометрический корень где a3 – коэффициент при старшей степени характеристического полинома, a0 – свободный член характеристического полинома. Степень устойчивости Колебательность Время переходных процессов Tп. Т.к. ближе к оси мнимых чисел Im находится пара комплексно-сопряжённых корней, то время переходных процессов определяется следующим образом где δ = 0.05. Величина затухания Для определения полосы пропускания системы и запасов устойчивости по фазе и по амплитуде строятся логарифмическая амплитудно-частотная характеристика (ЛАЧХ) и логарифмическая фазово-частотная характеристика (ЛФЧХ) (рис. 2.3). 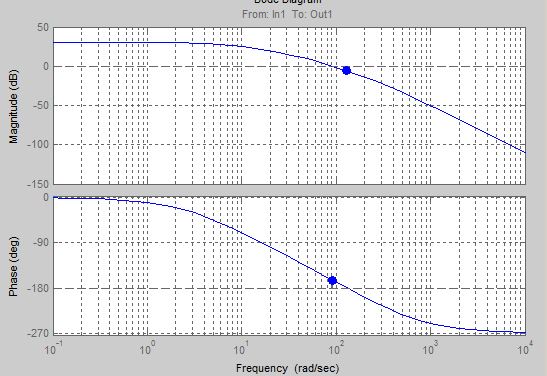 Рис. 2.3. ЛАЧХ и ЛФЧХ ОУ Ниже приведены частотные показатели качества объекта управления. Частота среза ωС = 91.2 рад/с. Полоса пропускания (0 – ωП) = (0 – 91.2) рад/с. 3. Запас устойчивости по амплитуде ΔA = 5.88 дб на частоте ω = 129 рад/с. Запас устойчивости по фазе Δφ = 14.8° на частоте ω = 91.2 рад/с. Также оценка динамических характеристик объекта проводится временными показателями качества. Для этого с помощью программного комплекса MatLab (рис. 2.4) строятся графики переходных процессов по скорости (рис. 2.5) и току (рис. 2.6). При этом на вход системы подаётся управляющее воздействие Uу = 1 В при t = 0 с и в установившемся режиме (в данном случае при t = 7 с) нагрузочный момент сопротивления Mc = 19.6 Н∙м. 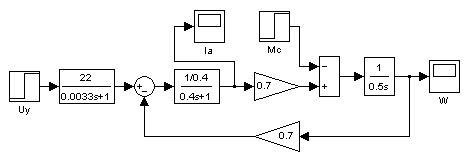 Рис. 2.4. Расчетная модель объекта управления 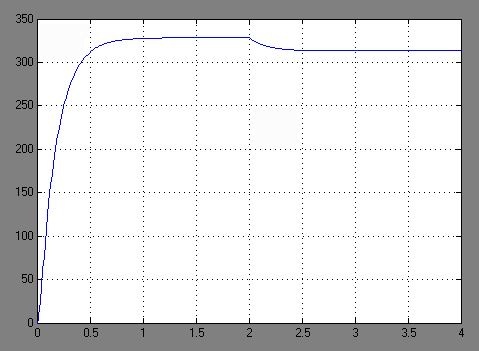 Рис. 2.5. Переходная характеристика ОУ по скорости 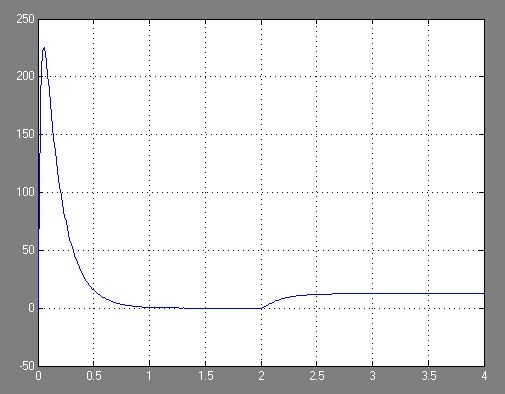 Рис. 2.6. Переходная характеристика ОУ по току По полученной характеристике ОУ по скорости (рис. 2.5) определяются временные показатели качества, которые должны удовлетворять заданным техническим требованиям к САУ. Время нарастания (время достижения установившегося значения первый раз): Tн = 0.5 с. Время достижения первого максимума: Tм = 1.1 с. Время регулирования или время переходного процесса (время вхождения в 5%-й коридор от установившегося значения): Tп = 0.5 с. Перерегулирование скорости Статическая ошибка стабилизации скорости 6. Время восстановления скорости при ступенчатом изменении момента нагрузки от нулевого до максимального значения (время возврата скорости к значению, равному Из графика переходного процесса по скорости видно, что статическая ошибка стабилизации скорости практически в 10 раз превышает максимально допустимую: Анализ статических и динамических характеристик ОУ показывает, что САУ соответствует не всем заданным техническим требованиям. Следовательно, для обеспечения желаемого качества переходных процессов в данной системе необходим синтез регулятора. Синтез последовательного корректирующего устройства (КУ) методом ЛАЧХ. Исследование качества переходных процессов замкнутой САУ 2.2.1. Синтез аналогового варианта последовательного корректирующего устройства ЛАЧХ исходной системы строится по передаточной функции ОУ: из характеристического полинома которой определяются сопрягающие частоты системы. 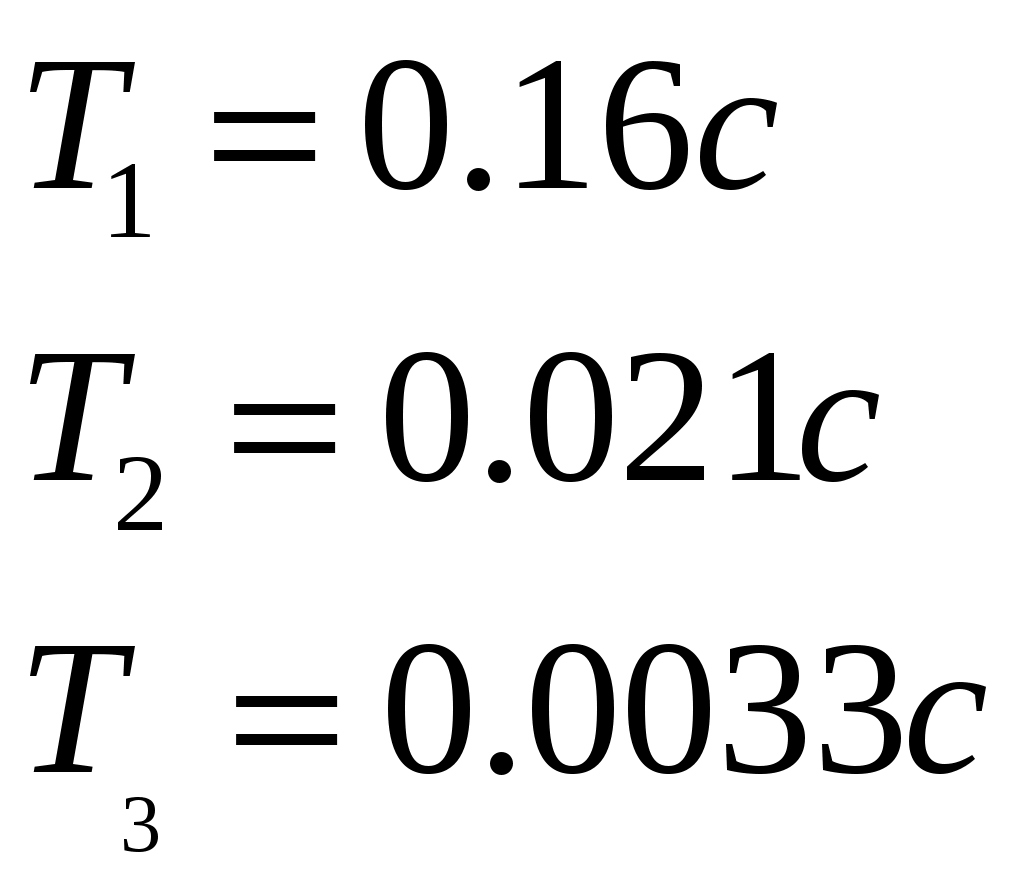 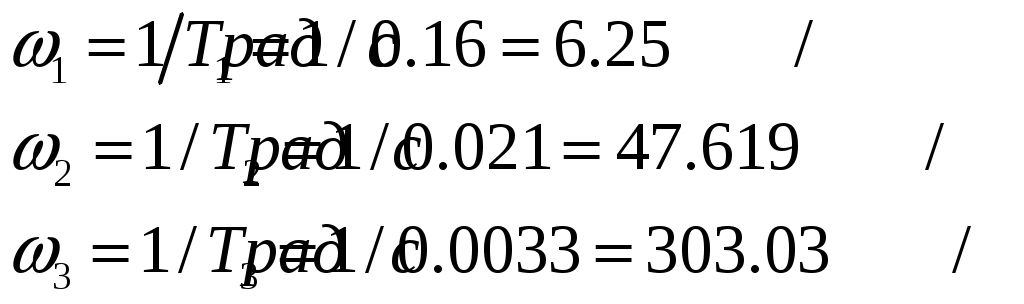 Сопрягающей частоте ω1, ω2, ω3 соответствует наклон -20 дб/дек, т.к. полином 1-го порядка. (рис. 2.7). Горизонтальный участок ЛАЧХ исходной системы проходит на уровне ЛАЧХ нескорректированной системы в низкочастотной (НЧ) области строится с таким петлевым усилением, который обеспечивает заданные требования к статической ошибке стабилизации скорости в установившемся режиме. По заданию статическая ошибка составляет Для получения требуемой статической ошибки стабилизации скорости коэффициент петлевого усиления системы должен составлять Исходя из этого, определяется коэффициент усиления регулятора (КУ) добавочный Горизонтальный участок ЛАЧХ нескорректированной системы проходит на уровне Далее ЛАЧХ нескорректированной системы идет параллельно ЛАЧХ исходной системы, т.е. имеет одинаковые с ней частоты точек перегиба и наклоны участков ЛАЧХ. Среднечастотная (СЧ) часть ЛАЧХ желаемой системы является наиболее важной, т. к. определяет качество переходных процессов. Основные параметры СЧ-асимптоты – это её наклон и частота среза ωС. Частота среза определяет быстродействие системы. Чем больше ωС, тем выше быстродействие, тем меньше время переходного процесса Tп. ЛАЧХ желаемой системы должна удовлетворять заданному быстродействию. По заданию полоса пропускания САУ составляет f = 30 Гц. Следовательно, соответствующая ей частота среза Чем больше наклон СЧ-асимптоты, тем труднее обеспечить хорошие динамические свойства системы. Поэтому для обеспечения требуемого качества переходного процесса наклон ЛАЧХ на частоте среза целесообразно выбрать равным -20 дб/дек (апериодическое звено первого порядка с нулевым перерегулированием). Наклон желаемой ЛАЧХ на частоте среза системы -20 дб/дек должен продолжаться как минимум на полдекады влево и полдекады вправо от частоты среза. В данном случае участок желаемой ЛАЧХ с наклоном -20 дб/дек продолжен влево до пересечения с уровнем горизонтального участка ЛАЧХ нескорректированной системы (частота Высокочастотная часть (ВЧ) желаемой ЛАЧХ незначительно влияет на динамические свойства системы. Вообще говоря, лучше иметь возможно больший наклон её асимптот, что уменьшает требуемую мощность исполнительного органа и влияние высокочастотных помех. Часто при расчёте ВЧ-часть ЛАЧХ не принимают во внимание и строят совпадающей с ВЧ-частью исходной системы. Построение ЛАЧХ приведено на рис. 2.7. 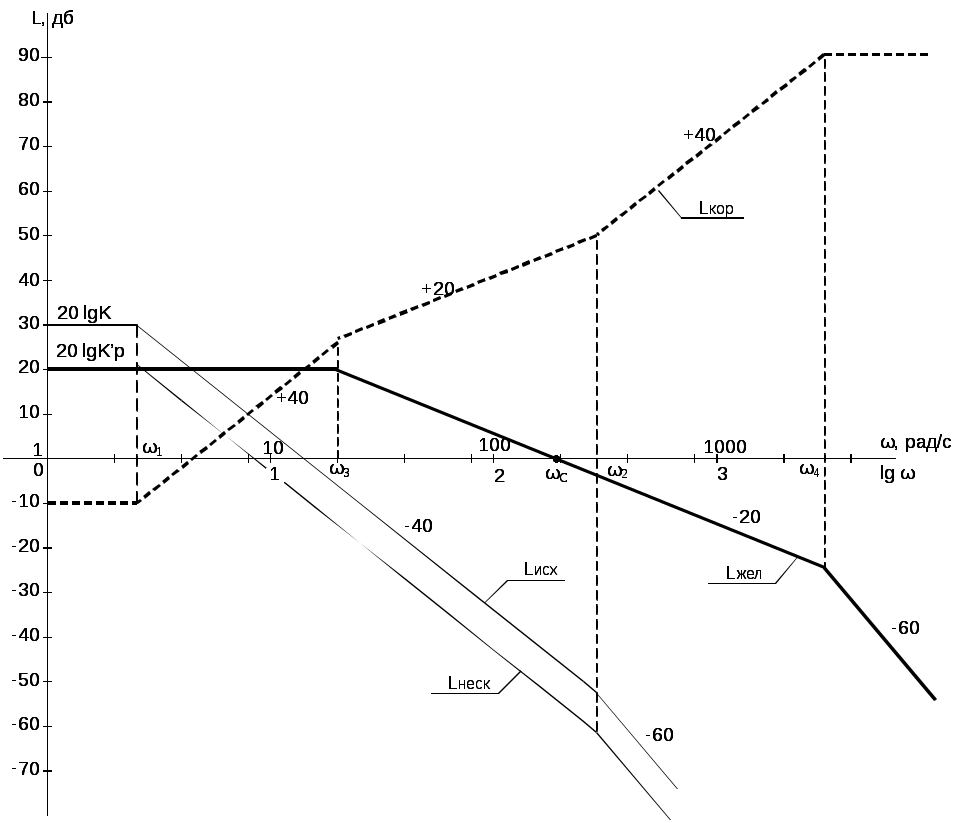 Рис. 2.7. Синтез корректирующего устройства методом ЛАЧХ ЛАЧХ корректирующего устройства получается путём вычитания из желаемой ЛАЧХ ЛАЧХ исходного объекта по участкам Сопрягающим частотам в точках перегиба ЛАЧХ корректирующего устройства соответствуют постоянные времени   В результате получается следующая передаточная функция корректирующего устройства КУ включается последовательно с ОУ. Для приближения системы к реальной в обратную связь ставится тахогенератор с фильтром, представленные апериодическим звеном 1-го порядка с коэффициентом передачи датчика скорости Kдс = 0.05 В∙с и постоянной времени фильтра Tф = 0.001 с. Для вывода системы на номинальную скорость Ω = 300 рад/с при максимальном управляющем воздействии Uy = 10 В выполняется перераспределение коэффициентов КУ и ветви отрицательной обратной связи. Для чего в прямой ветви коэффициент усиления регулятора умножается на 33,08, а сигнал обратной связи делится на этот же коэффициент. Расчетная модель полученной САУ представлена на рис. 2.8.  Рис. 2.8. Расчетная модель объекта управления с корректирующим устройством С помощью программного комплекса MatLab (рис. 2.8) строятся переходные характеристики системы автоматического управления по скорости (рис. 2.9) и току (рис. 2.10). При этом на вход системы подаётся управляющее воздействие Uу = 1 В при t = 0 с и в установившемся режиме (в данном случае при t = 3 с) нагрузочный момент сопротивления Mc = 19.6 Н∙м. 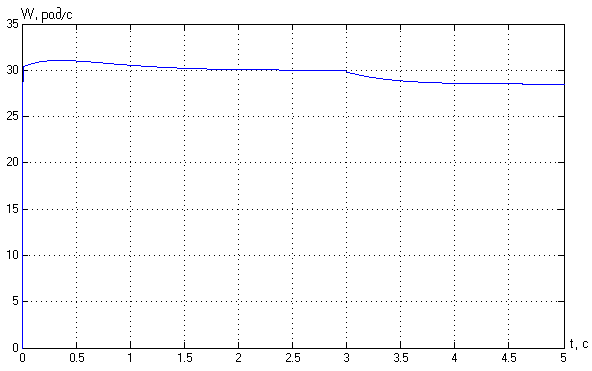 а)  б) 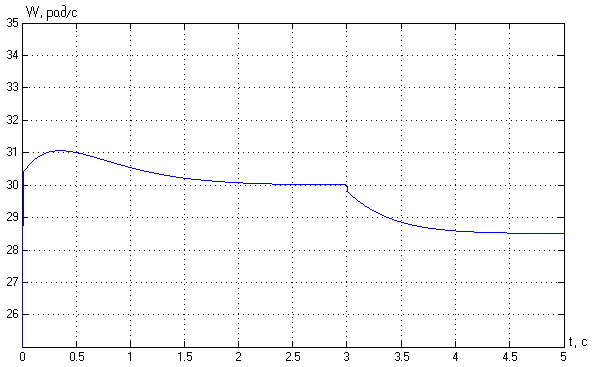 в) Рис. 2.9. Переходная характеристика по скорости ОУ с КУ: а) исходная характеристика; б) увеличенный фрагмент – отработка задания – увеличение по оси X начального участка; в) увеличенный фрагмент – отработка возмущения – увеличение по оси Y 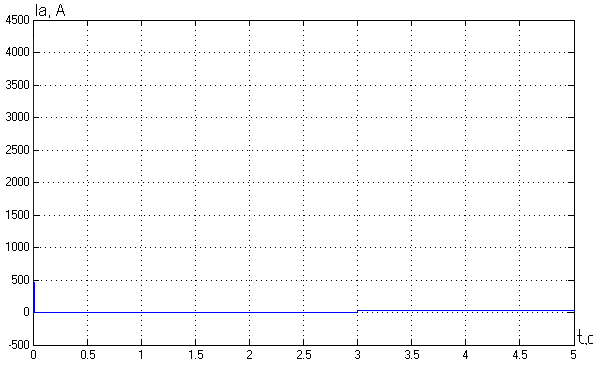 а) 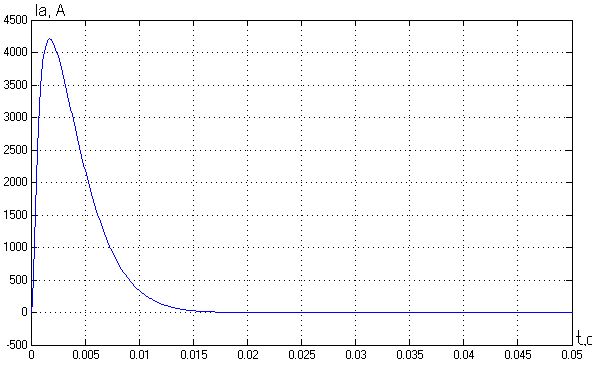 б) 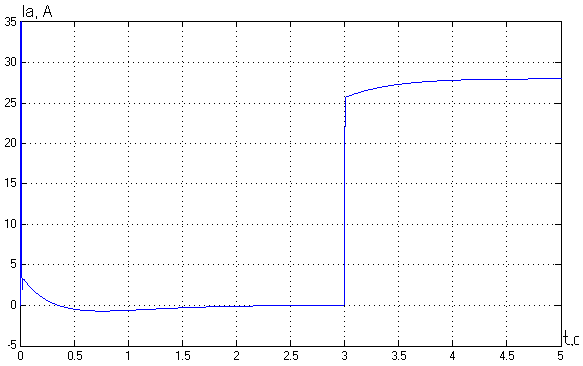 в) Рис. 2.10. Переходная характеристика по току ОУ с КУ: а) исходная характеристика; б) увеличенный фрагмент – отработка задания – увеличение по оси X начального участка; в) увеличенный фрагмент – отработка возмущения – увеличение по оси Y (при подаче момента нагрузки ток должен установиться на номинальном значении, в нашем случае Iн = 28 А !) По полученной переходной характеристике по скорости ОУ с КУ (рис. 2.9) определяются временные показатели качества. Статическая ошибка стабилизации скорости (определяется в процентах от максимальной скорости!) 2. Время переходного процесса: Tп = 0.009 с. 3. Время восстановления скорости при ступенчатом изменении момента нагрузки: Tв = 0. Перерегулирование скорости Заданным техническим требованиям удовлетворяют все временные показатели качества. В линейной зоне работы максимальный ток электродвигателя не должен превышать значения Iм = 3∙Iн = 3∙28 = 84 А при ступенчатом изменении управляющего сигнала. Для соблюдения этого условия на вход системы следует подавать управляющее воздействие, не превосходящее величины Uу = 0,02 В (определяется экспериментально). При этом скорость, на которую выходит двигатель, составляет Ω = 0,6 рад/с. (Здесь необходимо менять управляющее воздействие Uу, наблюдая за максимальным значением тока при пуске системы, до тех пор, пока максимальный бросок тока станет равным максимально допустимому току в электродвигателе Iм = 3∙Iн = 3∙28 = 84 А. !) 2.2.2. Синтез цифрового варианта последовательного корректирующего устройства и исследование влияния такта квантования по времени Осуществляется по аналоговому прототипу методом цифрового перепроектирования. Цифровое перепроектирование – это определение структуры и параметров цифрового регулятора по его аналоговому прототипу, обеспечивающих максимальное соответствие динамических характеристик непрерывной и дискретной систем. Это наиболее простой путь получения дискретного алгоритма управления. Переход к дискретному регулятору основывается на использовании z-форм для реализации динамической части регулятора. В данном случае используется приближённая формула Эйлера В результате подстановки для части КУ получается  . .Для целого КУ Дискретный регулятор будет эквивалентен непрерывному при выполнении теоремы Котельникова-Шеннона. Для этого такт квантования T0 должен быть хотя бы в два раза меньше, чем заданное время переходного процесса Tп = 0.033 с. Для более точного соответствия цифровой и аналоговой переходных характеристик при инженерных расчетах такт квантования выбирается в ( Расчётная модель полученной САУ с цифровым КУ приведена на рис. 2.11. (В программном комплексе MATLAB для дискретных передаточных функций используется блок Discrete Filter или Discrete Transfer Fcn. В этих блоках в настройках в последней строке «Sample time» необходимо указать такт квантования T0, который был использован для расчетов!) 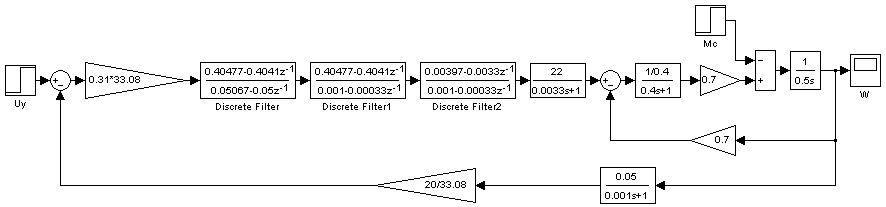 Рис. 2.11. Расчетная модель объекта управления с цифровым корректирующим устройством Получаем переходную характеристику системы автоматического управления по скорости (рис. 2.12). При этом, как и ранее, на вход системы подаётся управляющее воздействие Uу = 1 В при t = 0 с и в установившемся режиме (в данном случае при t = 3 с) нагрузочный момент сопротивления Mc = 19.6 Н∙м. Из полученного графика видно, что при выбранном такте квантования T0 = 0,00067 с переходный процесс в системе с цифровым корректирующим устройством (рис. 2.12) совпадет с переходным процессом в системе с аналоговым КУ (рис. 2.9, а). 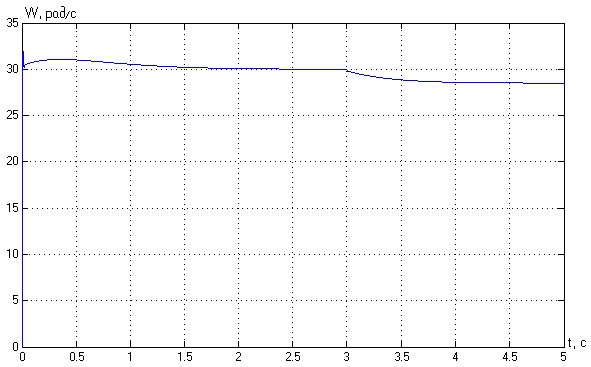 Рис. 2.12. Переходная характеристика ОУ с цифровым КУ (T0 = 0.00067 с) При увеличении такта квантования до T0 = 0.005 с качество процессов в системе с цифровым КУ существенно ухудшается, график переходного процесса по скорости в этом случае приведён на рис. 2.13. Следовательно, дальнейшее увеличение такта квантования в системе является нецелесообразным.  Рис. 2.13. Переходная характеристика ОУ с цифровым КУ (T0 = 0.005 с) Влияние нелинейностей регулятора, обеспечивающих ограничение тока электродвигателя и напряжения силового преобразователя Рассмотрим систему с непрерывным корректирующим устройством (рис. 2.8), полученным в п. 2.2.1. Как видно из графика переходного процесса (рис. 2.10, а, б) ток в системе при пуске значительно превышает максимально допустимое значение Iм = 3∙Iн = 3∙28 = 84 А. Для того чтобы при пуске электродвигателя на максимальную скорость ток не превышал максимально допустимого значения, на вход системы включают задатчик интенсивности, обеспечивающий линейное нарастание входного сигнала (рис. 2.14). Задатчик интенсивности состоит из двух блоков: - блок «Ramp» служит для получения необходимого темпа нарастания входного сигнала; - блок «Saturation» используется для ограничения входного сигнала по уровню, необходимо установить ограничение входного сигнала на уровне +/-10 В, что соответствует максимальной скорости вращения двигателя. Следует также обеспечить ограничение по напряжению электродвигателя, исходя из допустимого кратковременного превышения его номинального значения на 20 %. Для этого в схему на выход корректирующего устройства последовательно с ним включается ещё один блок «Saturation», но уже с параметрами +/-12 В, что соответствует максимальным броскам напряжения Uн = 220 В + 20 % = 220 + 0,2*220 = 264 В. Параметр «Slope» (наклон) блока «Ramp» определяется экспериментально. Его необходимо менять, наблюдая за максимальным значением тока при пуске системы, до тех пор, пока максимальный бросок тока станет равным максимально допустимому току в электродвигателе Iм = 3∙Iн = 3∙28 = 84 А. В нашем случае экспериментально было определено, что параметр «Slope» = 3,64. 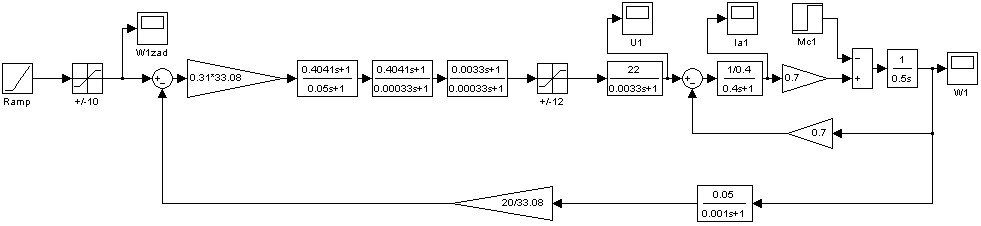 Рис. 2.14. Расчетная модель объекта управления с корректирующим устройством, задатчиком интенсивности и ограничением по напряжению С помощью программного комплекса MatLab (рис. 2.14) строятся графики переходных процессов системы по напряжению, току и скорости (рис. 2.15). При этом на вход системы подаётся управляющее воздействие Uу = 10 В при t = 0 с и в установившемся режиме (в данном случае при t = 7 с) нагрузочный момент сопротивления Mc = 19.6 Н∙м. 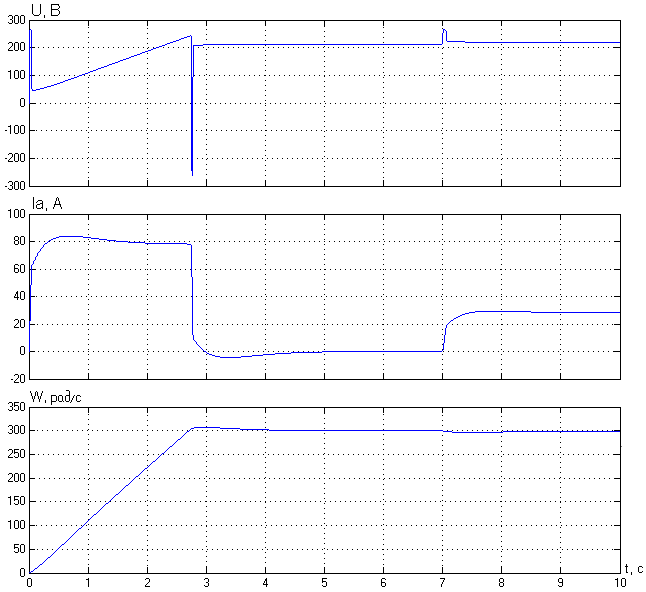 Рис. 2.15. Переходные характеристики по напряжению, току и скорости объекта управления с корректирующим устройством, задатчиком интенсивности и ограничением по напряжению Из полученных результатов видно, что при работе вне линейной зоны ток не превышает максимально допустимого значения Imax = 84 А, напряжение также находится в области допустимых значений ( Разработанная система управления будет реализована на микроконтроллере. |
