Практическое задание математика. 2. Решить уравнение, допускающее понижение порядка Пусть
 Скачать 66.05 Kb. Скачать 66.05 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Математика Группа Ив22ГУ171в Студент Кононова К.В МОСКВА 2023 1. Методом изоклин построить интегральные кривые уравнения 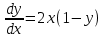 k=f(x, y) , где k=const Тогда k=2x(1-y) => 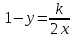 => =>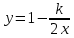 В данном случае, изоклины представляют собой семейство гипербол а) k = 0 =>y = 1 б) k = 1 => 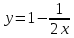 в) k = -1 => 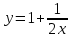 г) k=2 => 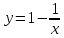 д) k=-2 => 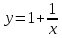 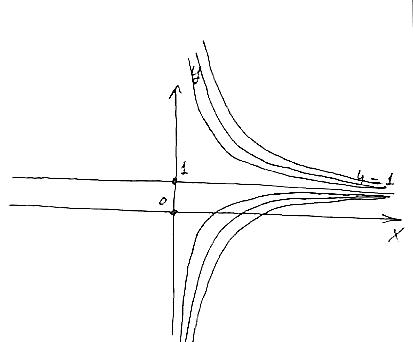 2. Решить уравнение, допускающее понижение порядка 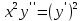 Пусть 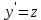 . Тогда . Тогда 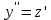 Получим 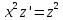 => =>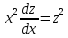 => =>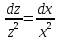 . .Проинтегрируем 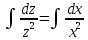 => =>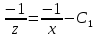 => =>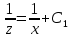 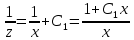 . . Отсюда 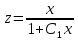 . . Так как 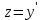 , то , то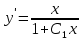 ; ; 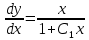 => =>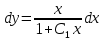 => =>y= 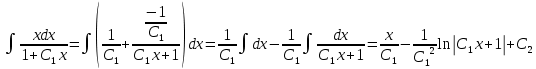 Ответ: 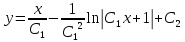 3. Решить систему уравнений 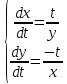 Находим 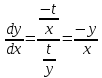 Отсюда 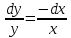 . . Интегрируем 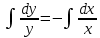 => =>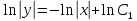 => =>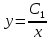 . Подставим в первое уравнение: . Подставим в первое уравнение: 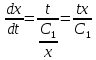 => =>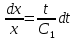 => =>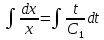 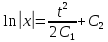 . . Отсюда 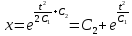 Подставляем во второе уравнение: 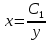 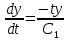 => =>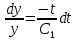 => =>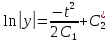 . .Отсюда 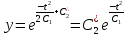 Ответ: 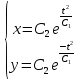 4.Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Для конкретного n наивероятнейшее число появлений события 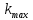 будет при условии: будет при условии: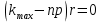 ; ; 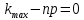 => =>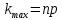 . .Отсюда: 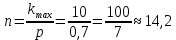 Ближайшее целое число к этому значению n=14 Ответ: 14 испытаний Здесь мы использовали формулу Муавра-Лапласа 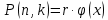 , где , где 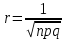 , , 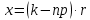 , , 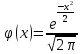 – функция Гаусса. – функция Гаусса.2 способ: Для нахождения n используем: 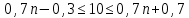 => =>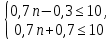 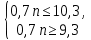 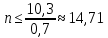 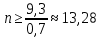 Т.е. 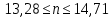 Целое число, которое находится в промежутке равно 14 Ответ: 14 испытаний. |
