Аннотация. 2 Второй способ заключается в определении модели температурного дрейфа и компенсирования его с помощью программных средств
 Скачать 2.68 Mb. Скачать 2.68 Mb.
|
|
Аннотация. Основные факторы, влияющие на температурный дрейф в волоконно-оптическом гироскопе, были проанализированы в этой статье. Была построена модель авторегрессии температурного дрейфа, связанная с температурой и скоростью изменения температуры. Коэффициенты модели могут быть получены путем наименьших квадратов. Эксперименты показывают, что модель была эффективна. В модели дрейфа тенденция дрейфа вызванная температурой может быть оценена. Температурный дрейф может быть компенсирован с помощь тенденции дрейфа. Результат эксперимента показывает, что ошибка дрейфа может быть уменьшена примерно на 87% после компенсации. Введение Волоконно-оптический гироскоп является новым видом измерительных приборов для измерения угловых скоростей, который основан на Эффекте Саньяка. С его преимуществом высокой точности, небольшими размерами, малым весом, ударопрочностью , устойчивым к вибрациям, и широким диапазоном измерения, волоконно-оптические гироскопы широко используются для измерения инерциальной системы наведения. Наряду с основным компонентам гироскопа чувствительные к температуре, так же на выходе гироскопа будут присутствовать шум и дрейф, зависящий от температуры окружающей среды. Для системы измерения отношение, которое принимает гироскоп в качестве основного компонента, шум, вызванный изменением температуры, может быть устранен после интегрирования, в то время как вызванный дрейф температуры принесет значительную ошибку в измерение угла ориентации [1]. Есть два способа компенсации температурного дрейфа гироскопа: 1) Первый способ основан на совершенствование аппаратной структуры по оптимизации гироскопа внутренней структуры и уменьшения чувствительности прибора к температуре [2]. 2) Второй способ заключается в определении модели температурного дрейфа и компенсирования его с помощью программных средств. На моделях температуры и компенсации ошибок для волоконно-оптического гироскопа Хан Bing и др. кратко представлена модель линейной и несколько моделей нейронных сетей [3,4]. Вэй Янь и Junpu Ван представили модель линейной регрессии между дрифтом и температурой [5,6]. Другие исследования также были сделаны для температурного дрейфа ВОГ, например, волна малой длительности чистой работы [7]. Из-за различной структуры и производственной процедуры оптоволоконных гироскопов, нет температурной модели, которая могла бы использоваться. В этой статье мы проанализировали основные факторы, которые вызывают температурный дрейф и построили модель для дрейфа, а затем предложили метод компенсации. Температурный эффект ВОГ Оптоволоконный гироскоп имеет высокую точность оптических компонентов, таким образом на него имеет большое влияние температура. Шьюп Д.М. когда-то указал, что в интерференционном оптоволоконном гироскопе изменение температуры, которое связано со временем, вызывает невзаимную ошибку фазы, и он также дает происхождение выражению о невзаимной ошибке фазы, которую называют Ошибкой Шупа [8,9].  Рисунок 1 Температурное возмущение катушки волокна Рис. 1 показывает что, когда два луча света интерферируют по часовой стрелке и против часовой стрелки соответственно, ошибка Shupe которая формируется на области dz далеко от конца: 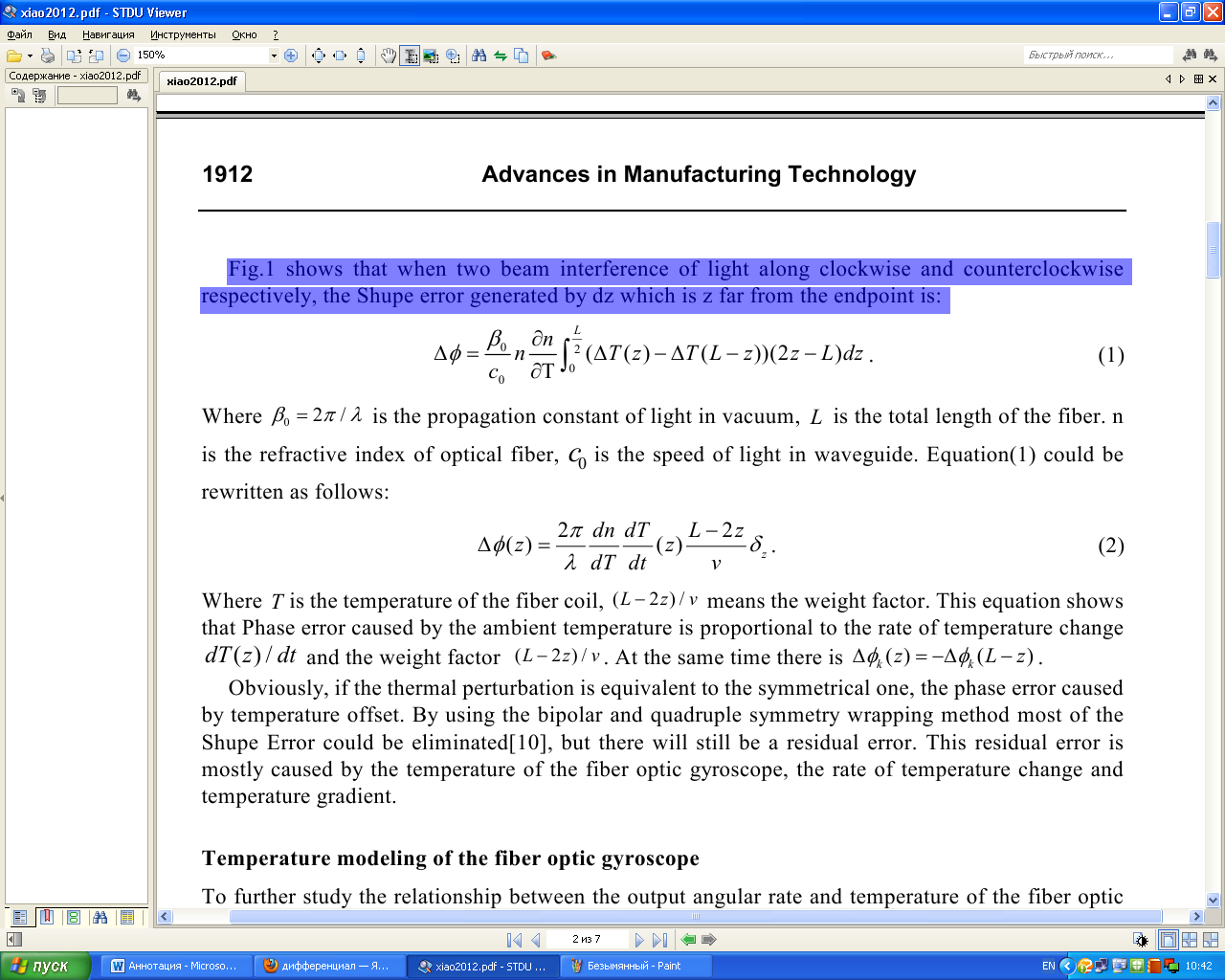 Где β0 = 2π / λ является распространением, постоянным света в вакууме, L - полная длина волокна. n - показатель преломления оптоволокна, c0 - скорость света в волноводе. Уравнение (1) может быть переписано следующим образом: 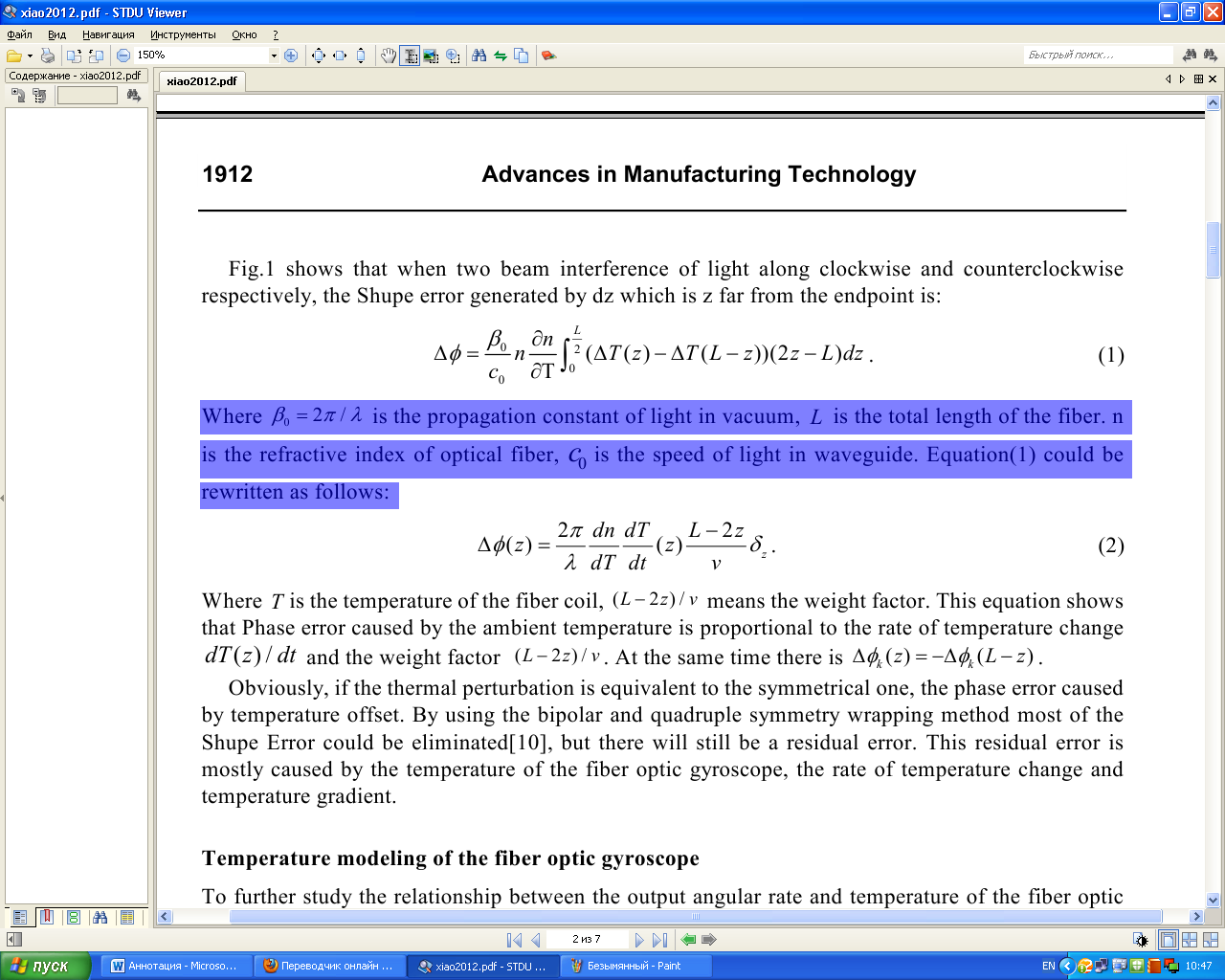 Где T - температура катушки волокна, (L − 2z) / v означает весовой фактор . Это уравнение показывает, что ошибка Фазы, вызванная температурой окружающей среды, пропорциональна уровню изменения температуры Td(z)/dt и фактору веса (L − 2z) / v. В то же время есть ∆ φk (z) = − ∆φk (L − z). Очевидно, что если тепловое изменение равноценно симметричному, то фазовая ошибка, вызванная температурой компенсируется. При помощи дипольного и квадрупольного метода симметричной намотки катушки ошибка Shupe может быть устранена [10], но все еще будет остаточная ошибка. Эта остаточная ошибка главным образом вызвана температурой оптоволоконного гироскопа, уровнем изменения температуры и температурного градиента. Температурное моделирование оптоволоконного гироскопа Чтобы далее изучить отношения между угловой скоростью и температурой оптоволоконного гироскопа, были проведены некоторые эксперименты. Как это показано на рисунке 2, одноосевой волоконно-оптический гироскоп был установлен на фиксированной горизонтальной плоскости и был запущен в течении часа, и в то же время мы варьируем температуру гироскопа от 15 ℃ до 70 ℃, используя температурное управляющее устройство. На выходе ВОГ содержится как сигнал угловой скорости, так и температурный сигнал, и они переведены в компьютер через интерфейс RS232 со скоростью передачи в бодах 38400 Bd/s.   Температура и угловая скорость Гироскоп Блок контроля температуры Инструкции по управлению Рисунок 2 Схема эксперимента Частота на выходе гироскопа составляет приблизительно 300 Гц с такой высокой скоростью передачи в бодах, которая вызовет большой объем данных, чтобы облегчить исследование, мы делаем обработку данных приблизительно в одну секунду для обоих. 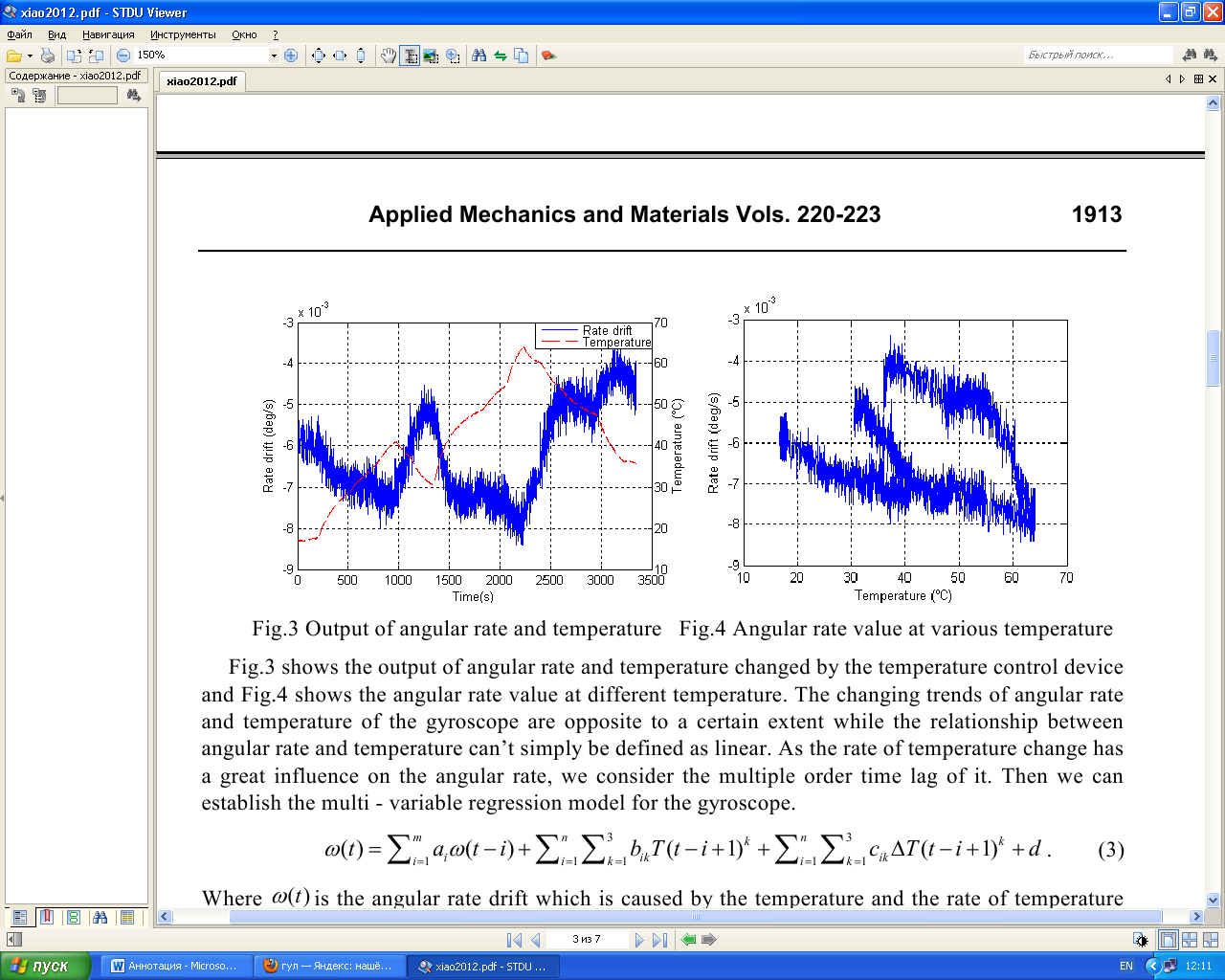 Рисунок 3 Температура и угловая скорость на выходе Рисунок 4 Угловая скорость при разной температуре На Рис. 3 показана угловая скорость и температура на выходе, измененный температурным управляющим устройством, на Рис. 4 показана угловая скорость при различной температуре. Изменяющиеся отклонение угловой скорости и температуры гироскопа известны, однако отношения между угловой скоростью и температурой не могут просто быть определены как линейные. Поскольку изменение температуры имеет большое влияние на угловую скорость, мы рассматриваем многократную временную задержку от нее. Тогда мы можем установить часто – изменяющуюся регрессионную модель для гироскопа. Где ω (т) является угловой скоростью дрейфа, которая вызвана температурой и скоростью изменения температуры; d является постоянной дрейфа; T (t) температура; ΔТ(т - j) является скоростью изменения температуры. Так как время выборки 1 секунда скорость изменения температуры могут быть вычислены по следующей формуле: Авторегрессия угловой скорости m порядка и регрессивная скорость изменения температуры n порядка имеет критическое значение для модели. Чем больше порядок, тем более точным является модель. Но чем больше порядка расчета , тем сложнее его рассчитать. Чтобы определить наилучшее значение m и n,для эксперимента необходимо использовать разные m и n. 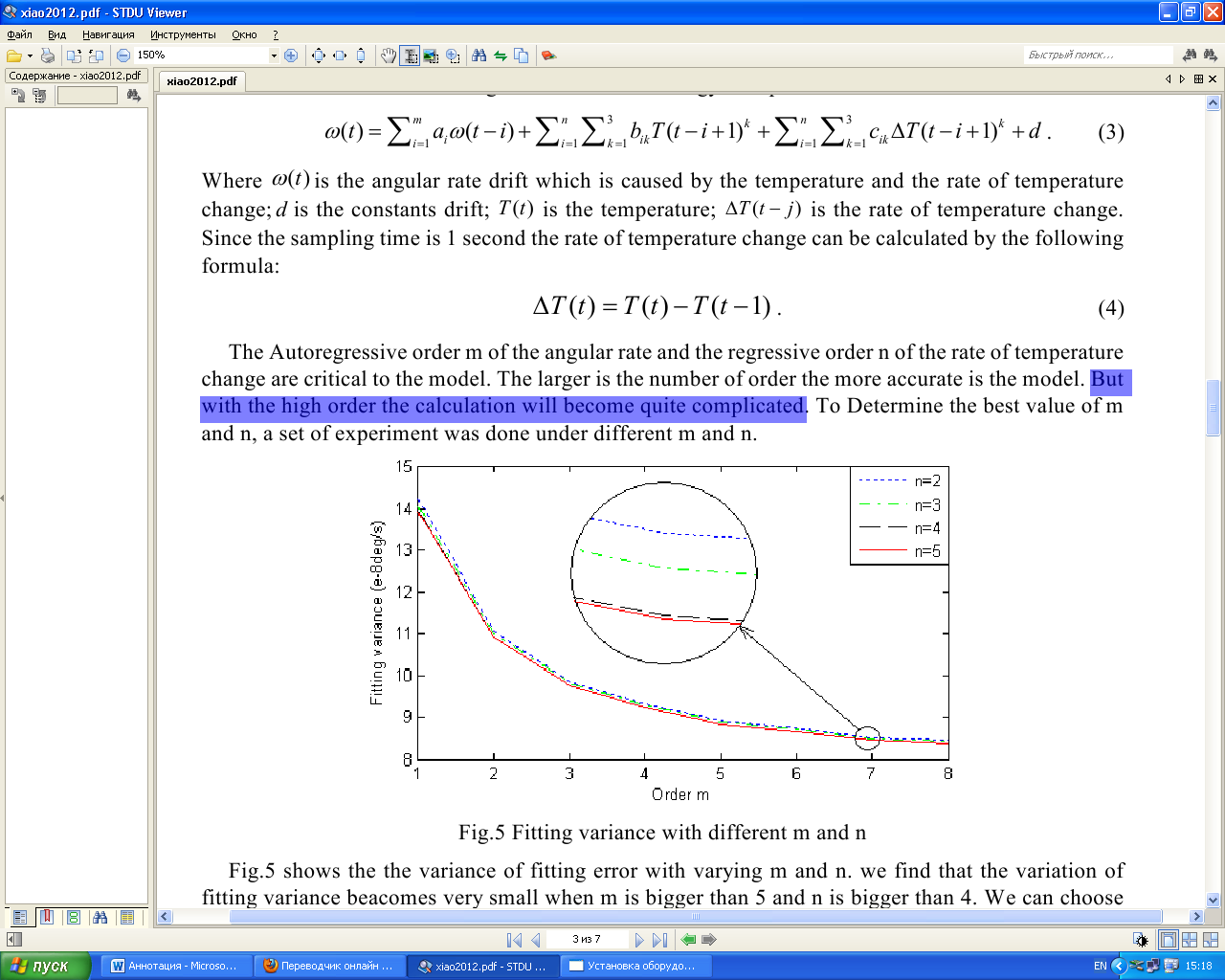 Порядок m  Рисунок 5 Дисперсия подгонки с различными n и m Рис.5 показывает изменение ошибки оборудования с переменным m и n. Мы видим, что изменение подгонки дисперсии становится очень маленький, когда m больше, чем 5 и n больше, чем 4. Мы можем выбрать количество регрессии со следующими порядками: M = 7, N = 4. Принимая нормальную температуру окружающей среды в качестве ориентира можно измерить константу дрейф нуля, который вызван вращением Земли и присущий смещению гироскопа. Значение измеренной постоянной дрейфа нуля является -0,0060107984690 град / с. После компенсации постоянного дрейфа нуля, мы можем получить угловую скорость дрейфа, которая зависит от температуры и от скорости изменения температуры. Красная прерывистая линия на рис.6 показывает реальную угловую скорость дрейфа после компенсации постоянной дрейфа нуля.  Время (с) 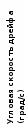 Рисунок 6 Реальная угловая скорость дрейфа и модель дрейфа З Таблица 1 начения параметров модели определенные температурой по формуле (3) могут быть получены из наименьших квадратов из реальных данных угловых скоростей. Рис.6 показывает результат многомерной регрессионной модели угловой скорости дрейфа. Это ясно видно из рисунка, что модель дрейфа хорошо соответствует реальному дрейфу, который доказывает высокую точность температурной модели дрейфа. 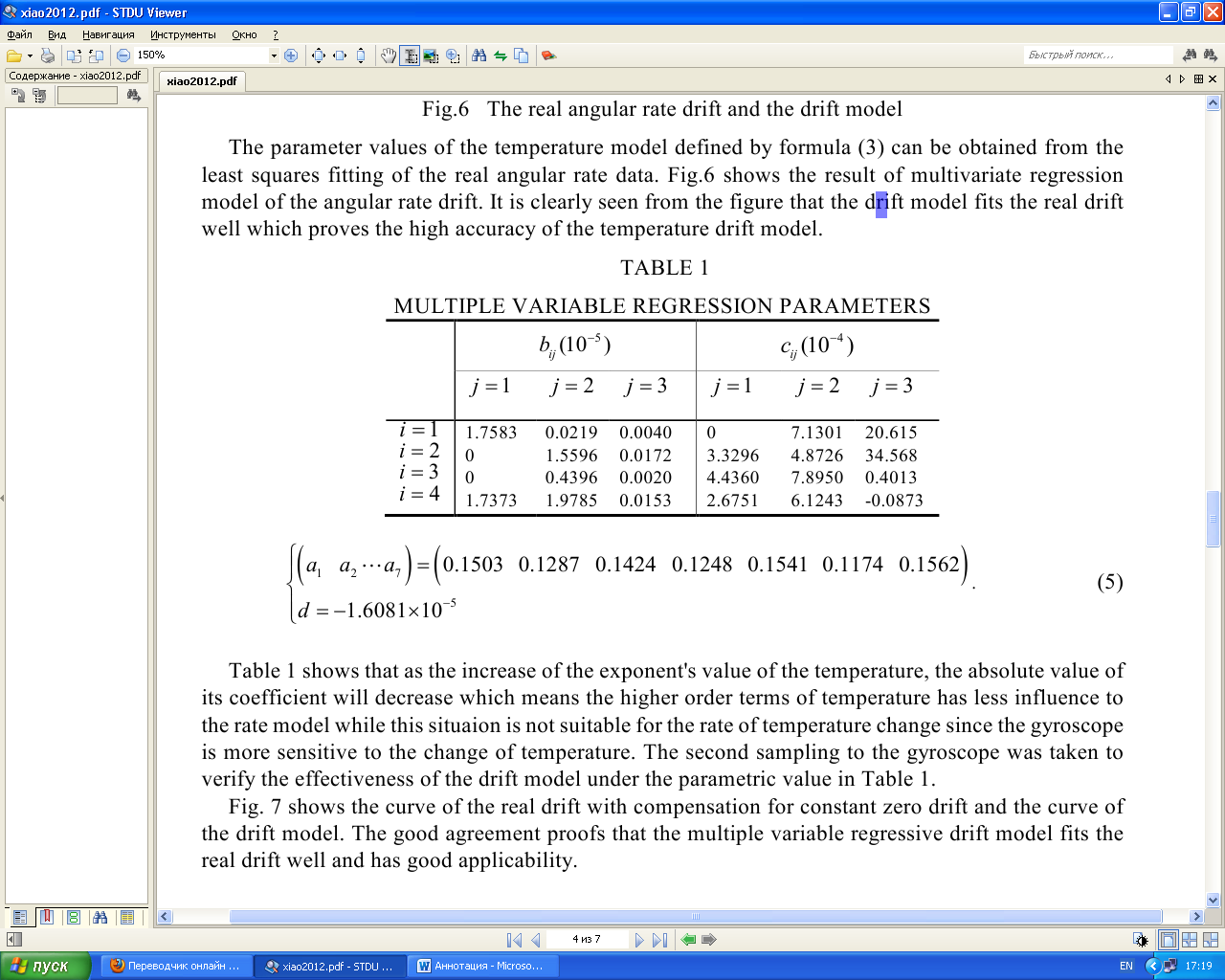 ПАРАМЕТРЫ ПЕРЕМЕННОЙ МНОГОКРАТНОГО РЕГРЕССА МНОГОКРАТНЫЕ ПЕРЕМЕННЫЕ ПАРАМЕТРЫ РЕГРЕССА МНОГОКРАТНЫЕ ПЕРЕМЕННЫЕ ПАРАМЕТРЫ РЕГРЕССА МНОГОКРАТНЫЕ ПЕРЕМЕННЫЕ ПАРАМЕТРЫ РЕГРЕССАМНОГОКРАТНЫЕ ПЕРЕМЕННЫЕ ПАРАМЕТРЫ РЕГРЕССА Таблица 1 показывает, что по мере увеличения значения показателя степени в части температуры, абсолютное значение его коэффициента снизится, который означает, что члены более высокого порядка температуры имеет меньшее влияние на модели скорости, а это положение не подходит для скорости изменения температуры так как гироскоп более чувствителен к изменению температуры. Вторая выборка в гироскопе была принята, чтобы проверить эффективность модели дрейфа по параметрическим значениям в таблице 1. На Рис. 7 показана кривая реального дрейфа с компенсацией для постоянного дрейфа нуля и кривой модели дрейфа. Хорошее доказательство того, что несколько переменных регрессионной модели дрейфа хорошо соответствуют реальной дрейфа и имеет хорошую применимость. 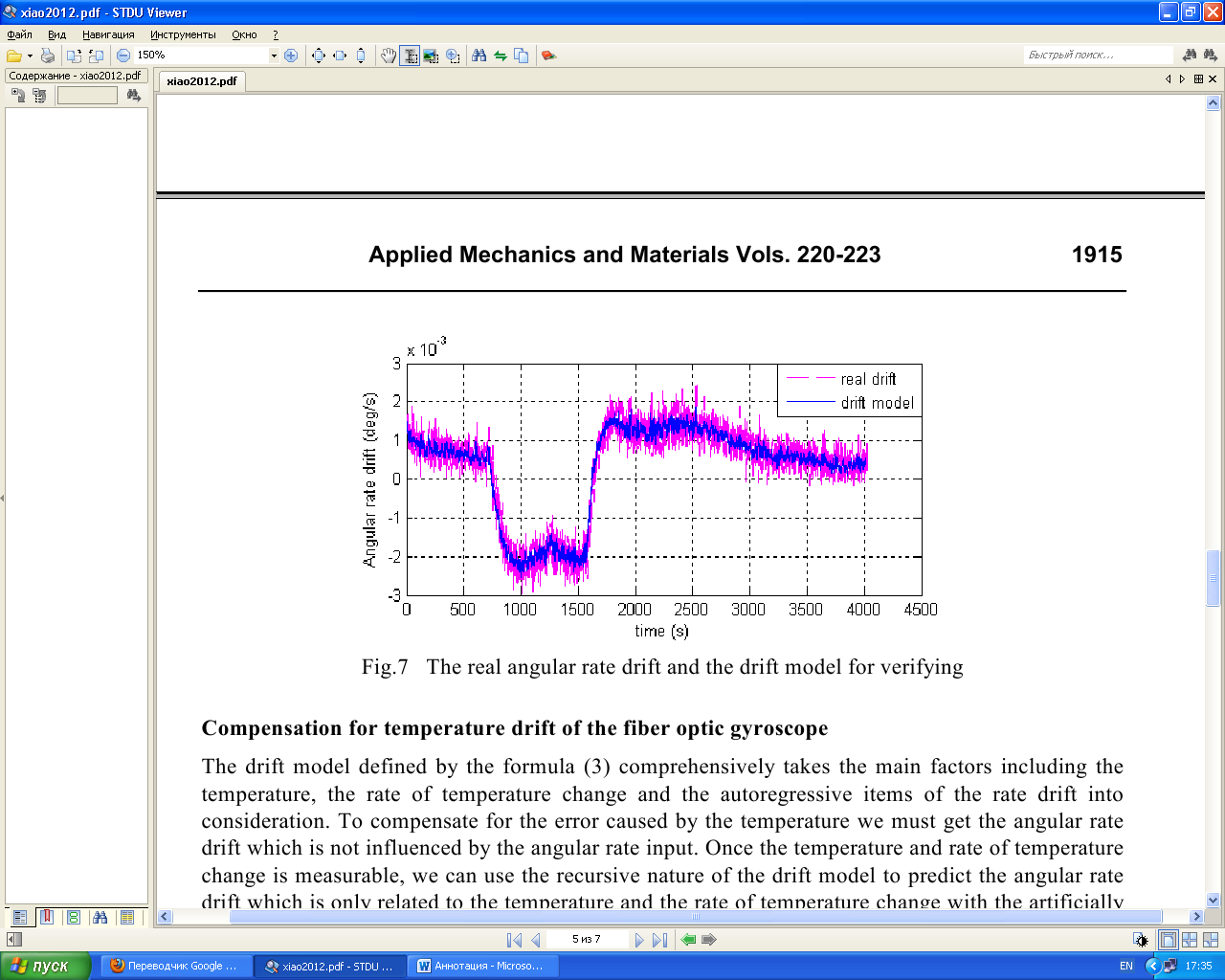 Рисунок 7 Реальная угловая скорость дрейфа и дрейфовая модель для проверки Компенсация температурного дрейфа волоконно-оптического гироскопа Модель дрейфа определяется по формуле (3) во внимание принимаются всесторонние основные факторы, включая температуру, скорость изменения температуры и авторегрессию, также скорость дрейфа. Чтобы компенсировать погрешности, вызванные температурой мы должны получить угловую скорость дрейфа, которая не зависит от входной угловой скорости. После того, как измерили температуру и скорость изменения температуры, мы можем использовать рекурсивную природу модели дрейфа предсказать угловую скорость дрейфа, которая связана с температурой и скоростью изменения температуры с заданными начальными данными угловой скорости. На Рис.8 показан процесс прогноза.  Прогнозная модель Рисунок 8 Прогнозная модель температурного дрейфа Для того чтобы проверить эффективность модели прогнозирования, мы проверили ее еще раз, чтобы гироскоп получил еще данные на выходе. И тогда мы должны проверить, соответствует ли модель прогнозирования реальному дрейфу. Принимая нормальную температуру окружающей среды в качестве точки отсчета, так же, как мы сделали это для моделирования угловой скорости позднее, мы продолжаем компенсировать постоянный дрейф нуля. В идеальном случае, если температура является постоянной, угловая скорость дрейфа должна быть равна нулю. Таким образом, начальное значение углового смещения может быть установлено в следующем виде: После рекурсивного вычисления, угловая скорость дрейфа модели прогнозирования может быть получена, как это показано на рис. 9. На рис.9 красная пунктирная линия представляет собой температуру на выходе гироскопа, а синей линией реальную расчетную скорость модели дрейфа. Сравнивая с реальной угловой скоростью дрейфа на выходе гироскопа на Рис.10 мы видим, что модель дрейфа можно точно прогнозировать дрейф угловой скорости. Рис. 10 показывает кривую ошибки после компенсации дрейфа скорости, вызванную температурой и скоростью изменения температуры. Средний дрейф до компенсации составляет около 1.366 град/ч, средний дрейф после компенсации 0.18 град / ч. Ошибка дрейфа уменьшается почти на 13% от исходной. По сравнению с результатами компенсации с линейной моделью компенсация улучшилась благодаря трех полиномиальной модели, особенно в ситуации температурных изменений. 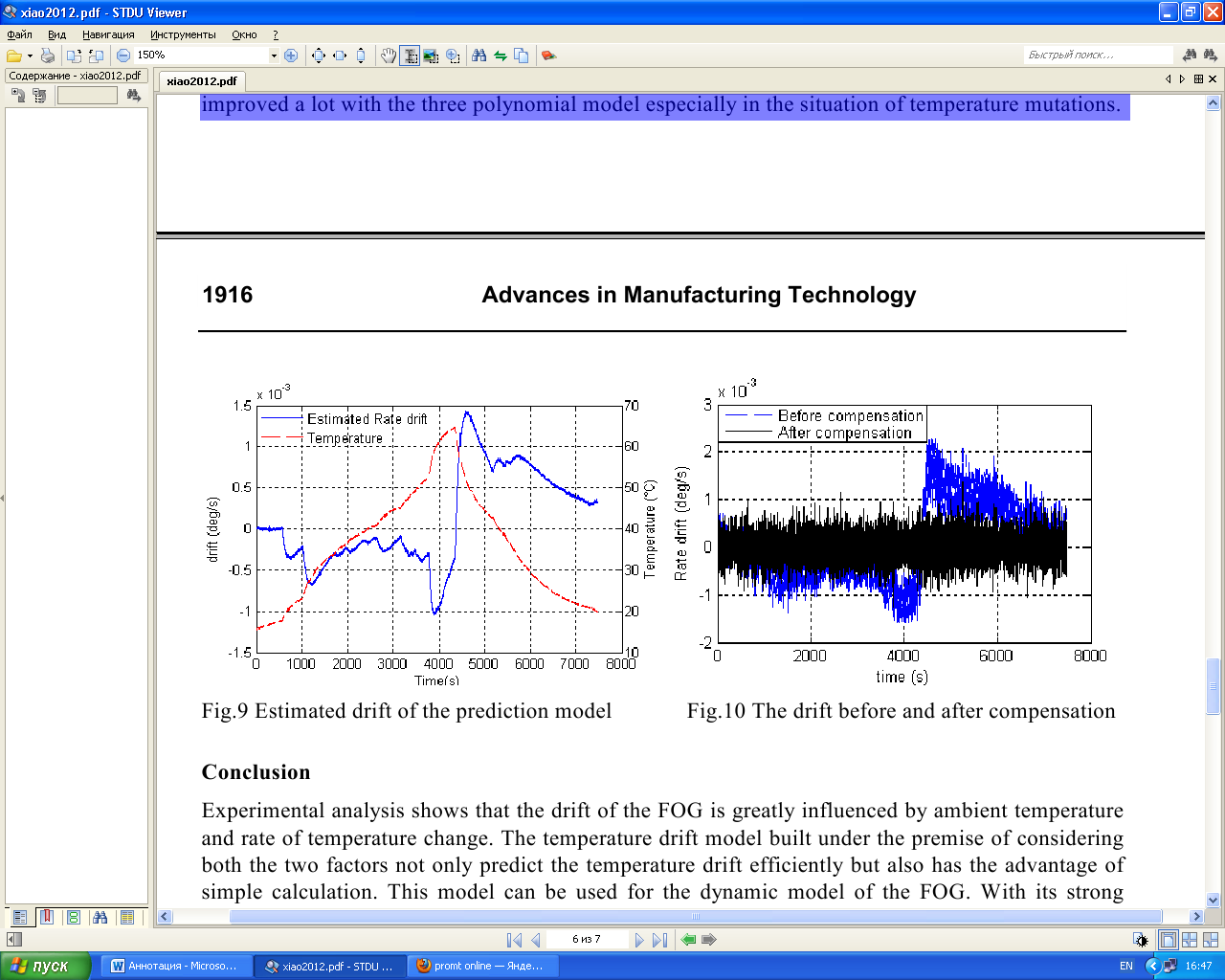 Рисунок 9 Расчетный дрейф модели прогнозирования Рисунок 10 Дрейф до и после компенсации Вывод Экспериментальный анализ показывает, что дрейф ВОГ сильно зависит от температуры окружающей среды и скорости изменения температуры. Температурная модель дрейфа, построенная принимая во внимание два фактора не только эффективно прогнозирует температурный дрейф, но также имеет преимущество простого расчета. Эта модель может быть использована для динамической модели ВОГ. Его сильные характеристики в режиме реального времени, могут быть широко использованы в инженерной практике. Исходя из эксперимента можно легко проанализировать, что эффект, вызванный изменением скорости температуры намного больше, чем эффект от температуры окружающей среды, так что изменение температуры ВОГ следует контролировать как можно больше в практическом применении. |
