финансовый менеджмент. Практическое задание Маскальчук. 2. Задача 1

• Название: 2. Задача 1
• Анкор: финансовый менеджмент
• Дата: 26.10.2022
• Размер: 200.54 Kb.
• Имя файла: Практическое задание Маскальчук.docx
• Тип: Документы; #755715
• страница: 5 из 9

Решение:

NPV определим по формуле: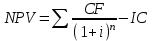

,

где 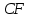- положительные денежные потоки по годам n;

i – ставка доходности;

IC – инвестиции.
Получаем:

- проект А: ;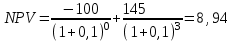

- проект Б: ;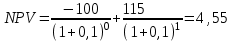

- проект В: ;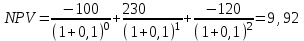

- проект Г: .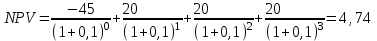
Ранжирование по NPV в порядке убывания:

1.Проект В;

2.Проект А;

3.Проект Г;

4.Проект Б.

Внутреннюю норму доходности (IRR) определим по формуле: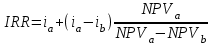

, где i – норма дисконта (i_a < IRR < i_b); NPV – чистая текущая стоимость (NPVa > 0 > NPVb).

Проект А. Рассчитаем NPV для ставок 13% и 14%.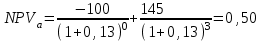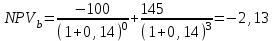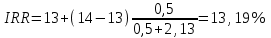

;

;



Проект Б. Рассчитаем NPV для ставок 15% и 16%.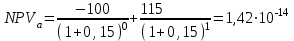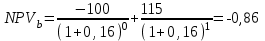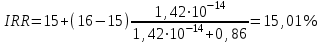

;

;

.

Проект В. Рассчитаем NPV для ставок 50% и 51%.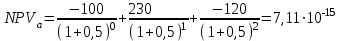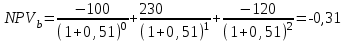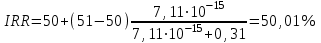

;

;

.

Проект Г. Рассчитаем NPV для ставок 15% и 16%.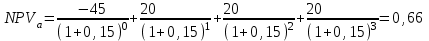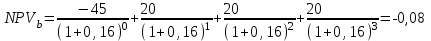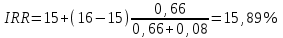

;

;

.

Ранжирование по IRR в порядке убывания:

1.Проект В;

2.Проект Г;

3.Проект Б;

4.Проект А.
Определим индекс рентабельности по формуле: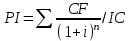



Получаем:

- проект А: ;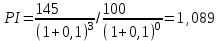

- проект Б: ;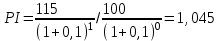

- проект В: ;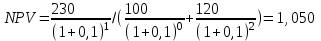

- проект Г: .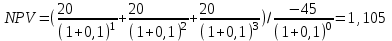
Ранжирование по PI в порядке убывания:

1.Проект Г;

2.Проект А;

3.Проект В;

4.Проект Б.

Таким образом, видно, что наиболее привлекательным проектом по критерию NPV оптимальным является проект В, по критерию PI – проект Г, по критерию IRR - проект В.
Анализ риска проекта

1. Корпорация рассматривает три возможных инвестиционных проекта на следующий год. Каждый проект рассчитан на один год, а доход от проекта зависит от состояния экономики в следующем году.

Ориентировочные оценки доходности проектов приведены ниже

Состояние экономики	Вероятность	Прогнозируемая доходность, %
		А	В	С
Спад	0,25	10	9	14
Средний уровень	0,5	14	13	12
Подъем	0,25	16	18	10

1) Рассчитайте ожидаемую доходность каждого проекта, дисперсию, среднее квадратическое отклонение и коэффициент вариации.

Решение:

Ожидаемую доходность каждого проекта определим по формуле:

d_ож=∑d_i×p_i, где d – доходность; р – вероятность.

Дисперсию определим по формуле:

σ²=∑(d_i- d_ож)²×p_i.

Среднее квадратическое отклонение определим по формуле: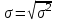

.

Коэффициент вариации определим по формуле: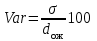

.

Получаем:

- для А: d_ож=0,25×10+0,5×14+0,25×16=13,5%;

σ²=0,25×(10-13,5)²+0,5×(14-13,5)²+0,25×(16-13,5)²=4,75;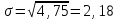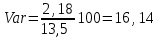

%;

%;

- для В: d_ож=0,25×9+0,5×13+0,25×18=13,25%;

σ²=0,25×(9-13,25)²+0,5×(13-13,25)²+0,25×(18-13,25)²=4,81;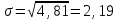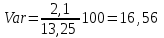

%;

%;

- для С: d_ож=0,25×14+0,5×12+0,25×10=12%;

σ²=0,25×(14-12)²+0,5×(12-12)²+0,25×(10-12)²=7;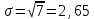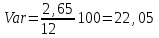

%;

%.
2. Проранжируйте альтернативы, исходя из:

i. Ожидаемой доходности;

ii. Риска.

Какой из предложенных альтернативных проектов следует принять?

Решение:

Проранжируем по ожидаемой доходности:

Проект А (13,5%) – 1

Проект В (13,25%) – 2

Проект С (12%) – 3.

Проранжируем по риску (коэффициент вариации):

Проект А (16,14%) – 1

Проект В (16,56%) – 2

Проект С (22,05%) – 3.

Из предложенных альтернативных проектов следует принять проект А, так как он имеет наибольшую ожидаемую доходность и наименьший относительный риск.
3.Имеются следующая информация по инвестиционному проекту:

Показатели	Год
	0	1	2	3	4
Инвестиции в основные средства, тыс. долл.	-240
Инвестиции в чистый оборотный капитал, тыс. долл.	-20
Объем реализации, ед.		1 250	1 250	1 250	1 250
Цена реализации, долл.		200	200	200	200
Валовой доход, тыс. долл.		250	250	250	250
Денежные операционные затраты (50%). тыс. долл.		-125	-125	-125	-125
Операционная прибыль, тыс. долл.		125	125	125	125
Амортизация, тыс. долл.		-79	-108	-36	-17
Прибыль до вычета процентов и налогов, тыс. долл.		46	17	89	108
Налоги (40%). тыс. долл.		-18		-36	-43
Чистый операционный доход, тыс. долл.		28	10	53	65
Амортизация, тыс. долл.		79	108	36	17
Ликвидационная стоимость, тыс. долл.		107	118	89	25
Налог на доходы от ликвидации имущества, тыс. долл.					-10
Возмещение вложений в оборотные средства, тыс. долл.					20
Чистый денежный поток, тыс. лолл.	-260	107	118	89	117