Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46
 Скачать 5.25 Mb.
|
Модель спроса и предложения и простейшая кейнсианская модель равновесия как системы одновременных уравнений.Ряд экономических процессов моделируется не одним, а несколькими уравнениями, содержащими как повторяющиеся, так и собственные переменные. В силу этого возникает необходимость использования систем уравнений. Кроме того, в одних уравнениях определенная переменная может рассматриваться как объясняющая (независимая), но в то же время она входит в другое уравнение как зависимая (объясняемая) переменная. Приведем ряд примеров таких систем. Модель 13.1. “спрос – предложение” Одна из простейших систем одновременных уравнений появляется при моделировании спроса – предложения в рыночной экономике. В этом случае в предположении, что спрос QD и предложение QS в момент времени t являются линейными функциями от цены P в этот же момент времени, мы получаем следующую систему: 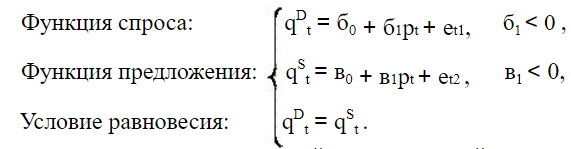 Очевидно, что наличие случайных отклонений в данных моделях связано в первую очередь с отсутствием в модели ряда важных объясняющих переменных (дохода, цен сопутствующих товаров, вкусов, ожиданий, цены ресурсов, налогов и т. д.). Изменение одного из этих факторов может отразиться на сдвиге одной либо обеих линий. Например, рост дохода потребителей может сдвинуть кривую спроса вверх (рис. 13.1). Это приводит к изменению равновесной цены и равновесного количества. 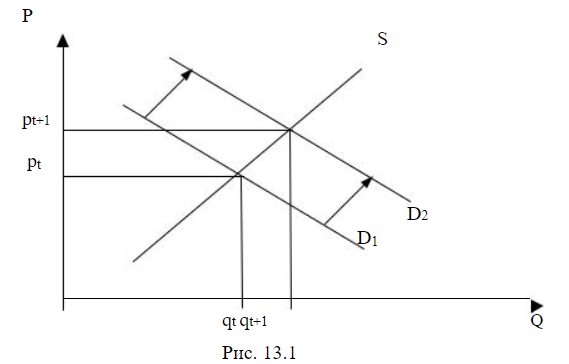 Модель 13.2. Кейнсианская модель формирования доходов Опишем простейшую модель данного типа в предположении, что рассматривается закрытая экономика без государственных расходов: 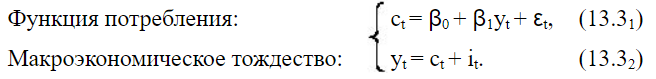 Здесь Y, C, I представляют совокупный выпуск, объемы потребления и инвестиций соответственно (yt, сt, it − значения этих переменных в момент времени t). Графическое представление систем одновременных уравнений.Систему взаимосвязанных тождеств ирегрессионных уравнений, в которой переменные могутодновременно выступать как эндогенные (результирующие) в однихуравнениях и как экзогенные (объясняющие) в других, принятоназывать системой одновременных эконометрических уравнений (СОУ). При этом в уравнения могут входить переменные, относящиеся к предшествующим моментам времени, которые называются лаговыми (запаздывающими). Классический МНК не применим к оцениванию параметров СОУ, поскольку нарушается предположение о независимости экзогенных и шоковых переменных. 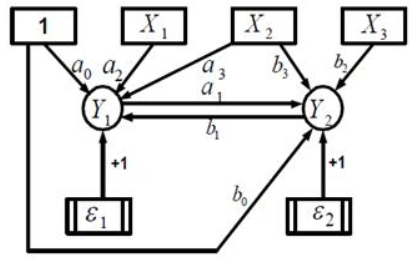 Приведем простой пример структурной СОУ, содержащей тождества. А на рис приведено удобное графическое изображение СОУ – причинная диаграмма, в которой экзогенные переменные помещаются в квадратах, а эндогенные – в кругах; взаимосвязи отмечаются стрелками с указанием коэффициентов при объясняющих переменных. 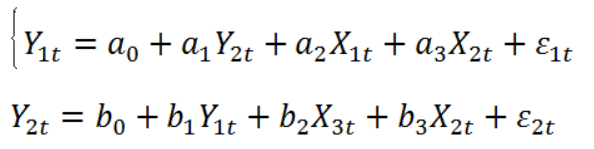 Заметим, что число уравнений и тождеств СОУ должно совпадать с числом эндогенных переменных. Структурная форма СОУ непосредственно неприменима для решения задач оценивания и прогнозирования, так как уравнения системы не разрешены относительно эндогенных переменных. Поэтому осуществляют преобразование структурной формы СОУ в так называемую приведённую форму, в которой правые части уравнений не содержат эндогенных переменных (т.е. выражаем Y). В общепринятом в литературе виде приведенная форма СОУ записывается: 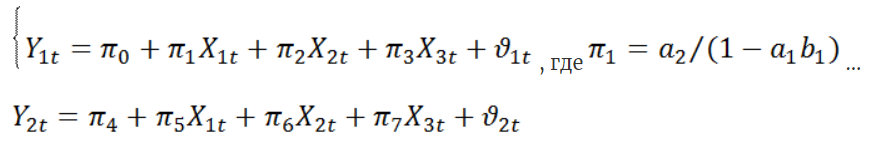 Здесь уже справедлива гипотеза о независимости шоковой и экзогенных переменных, и для оценивания мультипликаторовможно применить МНК, который носит название косвенного МНК,т.к. строит оценки для π, по которым надо еще пересчитатьоценки a и b. Напрмер:  .Однако, оценки, полученные по косвенному МНК, не являются несмещенными, поэтому разработан специальный двухшаговый МНК: 1 шаг) Преобразуем структурную форму СОУ к приведенной, к которой применим классический МНК. 2 шаг) Подставим в исходную структурную форму СОУ оценки эндогенных переменных и , полученные на предыдущем шаге алгоритма. К полученной СЭУ снова применим классический МНК, которые будут обладать свойствами несмещенности и асимптотической состоятельности. Коэфф приведенной формы наз-ют мультипликаторами, которые измеряют эффект воздействия стоящего при них сомножителя-экзогенной переменной на эндогенную, причем различают: •импульсные – измеряющие эффект воздействия экзогенной переменной на эндогенную в тот же период времени (t); •автономные - соответствуют свободному члену; •динамические - соответствуют коэфф при лаговой переменной. Матричное выражение СОМоделей, состоящих из n уравнений с n + m переменными: BY+CX=O; где  - вектор предопределенных (экзогенных и лаговыхэндогенных) переменных;  - вектор эндогенных переменных;  - матрица коэффициентов;  - матрица коэффициентов; O – нулевой вектор. |