Предположим, что значение заданной на отрезке 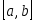 функции функции 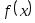 можно вычислить в произвольной точке можно вычислить в произвольной точке 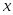 . Однако по некоторым причинам целесообразнее заменить прямое вычисление функции . Однако по некоторым причинам целесообразнее заменить прямое вычисление функции 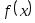 вычислением значений ее интерполяционного многочлена. Для такой замены необходимо один раз получить таблицу значений вычислением значений ее интерполяционного многочлена. Для такой замены необходимо один раз получить таблицу значений 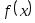 в выбранных точках в выбранных точках 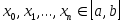 . При этом естественно стремиться к такому выбору узлов интерполяции, который позволит сделать минимальной величину . При этом естественно стремиться к такому выбору узлов интерполяции, который позволит сделать минимальной величину 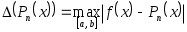 . .
Пусть о функции 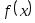 известно лишь то, что она непрерывно дифференцируема известно лишь то, что она непрерывно дифференцируема 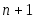 раз на отрезке раз на отрезке 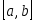 . Тогда . Тогда
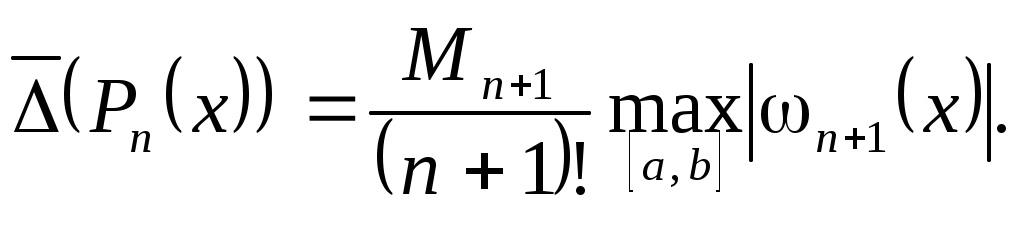 (3.6.1) (3.6.1)
Найдем теперь набор узлов интерполяции 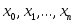 , при котором , при котором 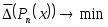 . Пусть сначала . Пусть сначала 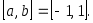 В этом случае величина (3.6.1) будет минимальна, если будет минимальна В этом случае величина (3.6.1) будет минимальна, если будет минимальна 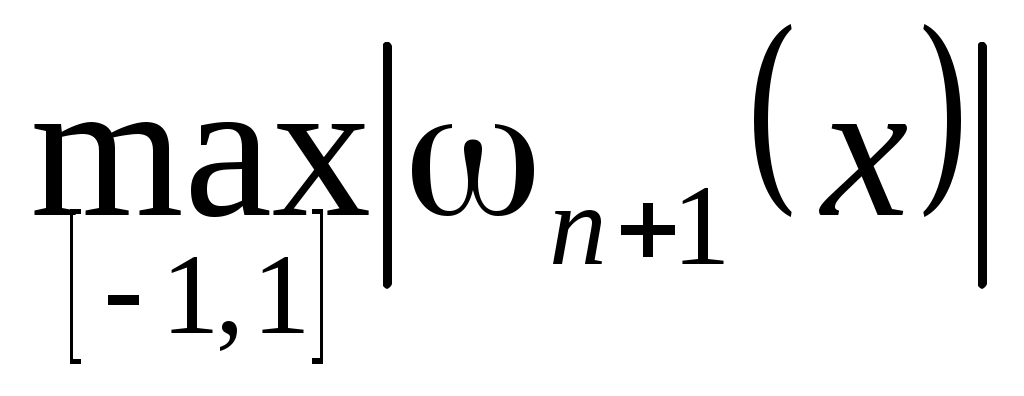 . Но этим свойством обладают полиномы Чебышева, следовательно, . Но этим свойством обладают полиномы Чебышева, следовательно, 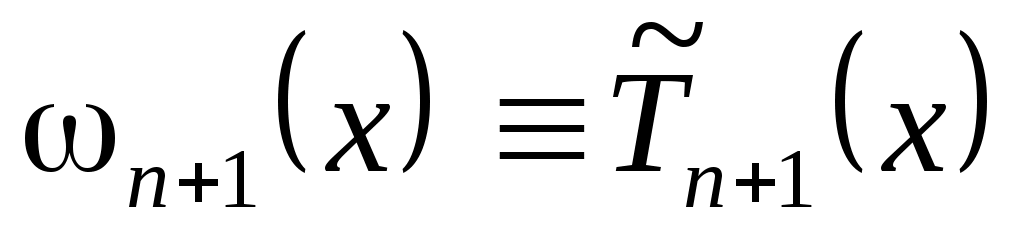 , и набор узлов определен , и набор узлов определен 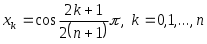 . Это нули многочлена . Это нули многочлена 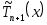 . При таком выборе . При таком выборе
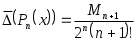 , (3.6.2) , (3.6.2)
причем любой другой выбор узлов дает большее значение верхней границы погрешности. Для формулы Тейлора, например, 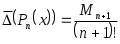 , то есть в , то есть в 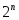 раз хуже. раз хуже.
Перейдем теперь к отрезку 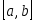 . Его можно преобразовать к стандартному отрезку . Его можно преобразовать к стандартному отрезку 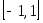 следующей заменой: следующей заменой: 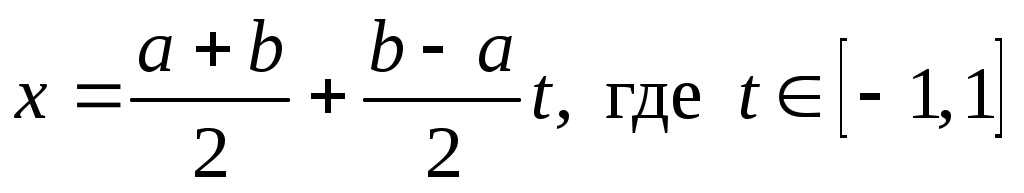 . В этом случае . В этом случае
 (3.6.3) (3.6.3)
Тогда 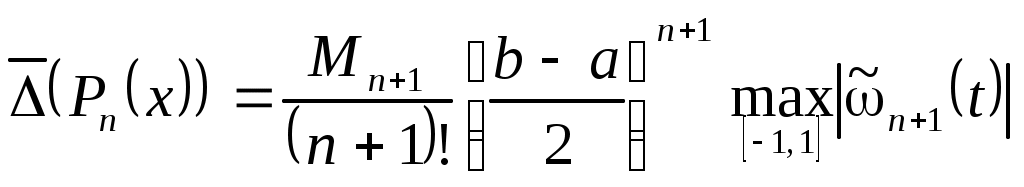 (3.6.4) (3.6.4)
и минимум этой величины достигается при значениях 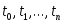 , совпадающих с нулями многочлена , совпадающих с нулями многочлена 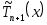 . Таким образом, решение поставленной задачи дает выбор узлов . Таким образом, решение поставленной задачи дает выбор узлов
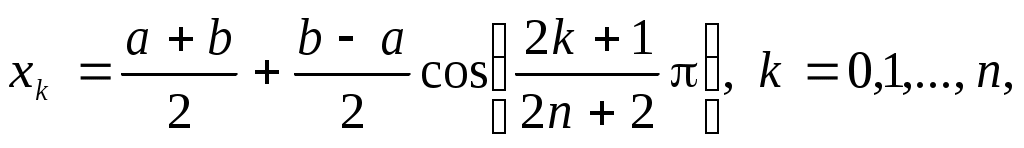 (3.6.5) (3.6.5)
и ему соответствует минимальное значение верхней границы погрешности интерполяции, равное: 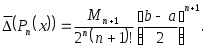 (3.6.6) (3.6.6)
|
 Скачать 2.21 Mb.
Скачать 2.21 Mb. (3.6.3)
(3.6.3)