методичка по КП. 3. Метод наименьших квадратов и специальные интерполяционные многочлены

• Название: 3. Метод наименьших квадратов и специальные интерполяционные многочлены
• Анкор: методичка по КП
• Дата: 18.05.2023
• Размер: 2.21 Mb.
• Имя файла: 3-3.7.doc
• Тип: Задача; #1142690
• страница: 3 из 6

3.3. Глобальная полиномиальная интерполяция

Пусть функция интерполируется на отрезке . Метод решения этой задачи единым для всего отрезка многочленом называется глобальной полиномиальной интерполяцией. Надежда приблизить везде на с заданной точностью единым многочленом базируются на теореме Вейерштрасса^.

Теорема 3.1. Пусть функция непрерывна на . Тогда для любого существует полином степени такой, что .

Однако существуют очень веские причины, по которым глобальная интерполяция многочленами высокой степени в вычислительной практике не используется. Обычный подход увеличения точности интерполяции - увеличение числа узлов. Однако не существует единой для всех непрерывных на отрезке функций стратегии выбора узлов интерполяции. Чаще всего узлы располагаются на равномерно. Но даже для очень гладких функций это иногда не приносит желаемого эффекта.

Классический пример - функция Рунге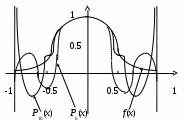^ . Если использовать глобальную аппроксимацию на с равномерным распределением узлов, то при больших n интерполяция дает очень хорошие результаты в центральной части отрезка. В то же время последовательность расходится при для (см. рисунок с лева). Таким образом, равномерное распределение узлов оказалось неудачным. Итак, не существует единой для всякой функции стратегии выбора узлов интерполяции. Об этом же говорит и теорема Фабера^.

Теорема 3.2. Какова бы ни была стратегия выбора узлов интерполяции,
найдется непрерывная на отрезке функция , для которой

Однако если функция гладкая (непрерывно дифференцируемая), то такая стратегия существует.

Теорема 3.3. Пусть в качестве узлов интерполяции на отрезке выбираются узлы полиномов Чебышева^. Тогда для любой непрерывно дифференцируемой на отрезке функции метод интерполяции сходится.

Практическая реализация стратегии выбора узлов интерполяции возможна и оправдана в довольно редких случаях и просто невозможна тогда, когда приходится иметь дело с заданной таблицей значений функции.