методичка по КП. 3. Метод наименьших квадратов и специальные интерполяционные многочлены
 Скачать 2.21 Mb. Скачать 2.21 Mb.
|
3.7. Ряд Фурье1 по многочленам ЧебышеваФункциональный ряд вида 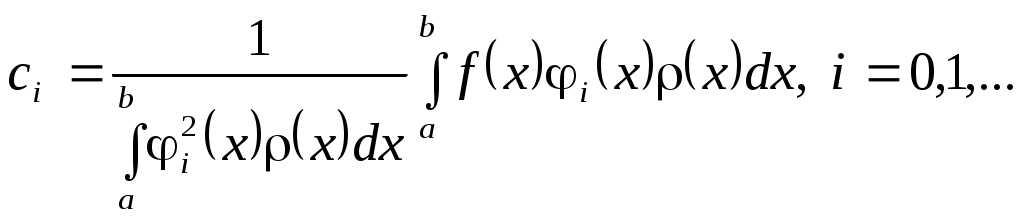 (3.7.1) (3.7.1)Так как для полиномов Чебышева весовая функция равна: то 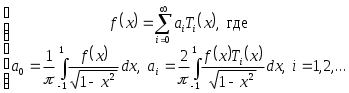 (3.7.2) (3.7.2)Пример. Разложить в ряд Фурье по полиномам Чебышева функцию Функция 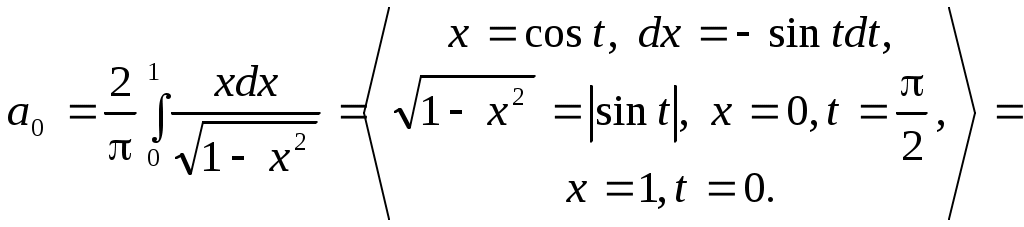  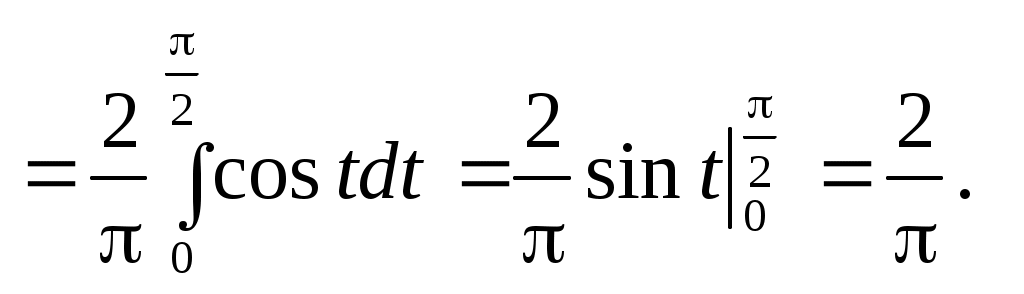 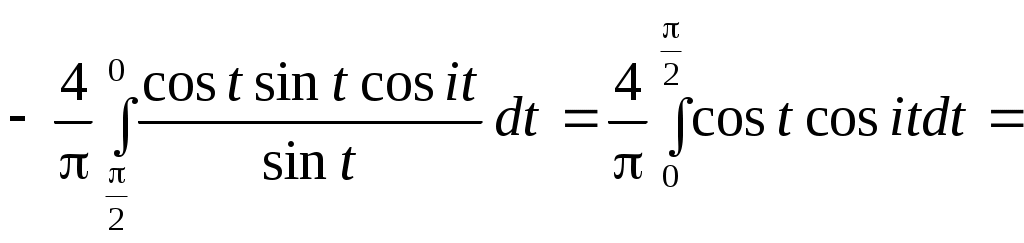 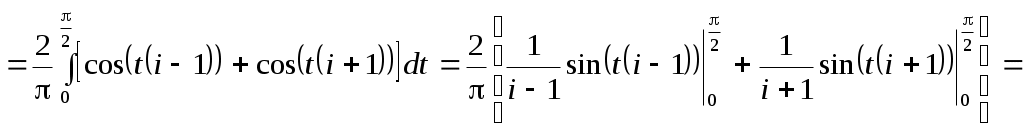 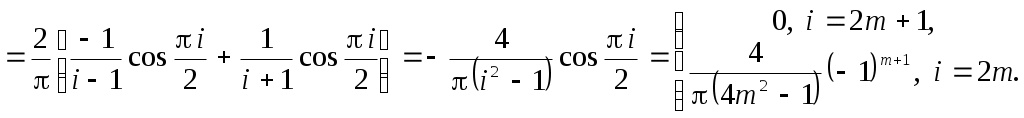 Итак, Пример. По равномерной (а) и специальной (б) таблице значений функции (а)
(б)
Так как таблицы короткие, то по ним можно вычислить разделенные разности лишь до четвертого порядка. Точки аргумента в таблице (б) - это нули многочлена Чебышева пятой степени, то есть точки, где     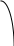 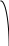 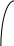 1 1    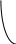      0.1 1.1 2.1 -1 1 -1 -1 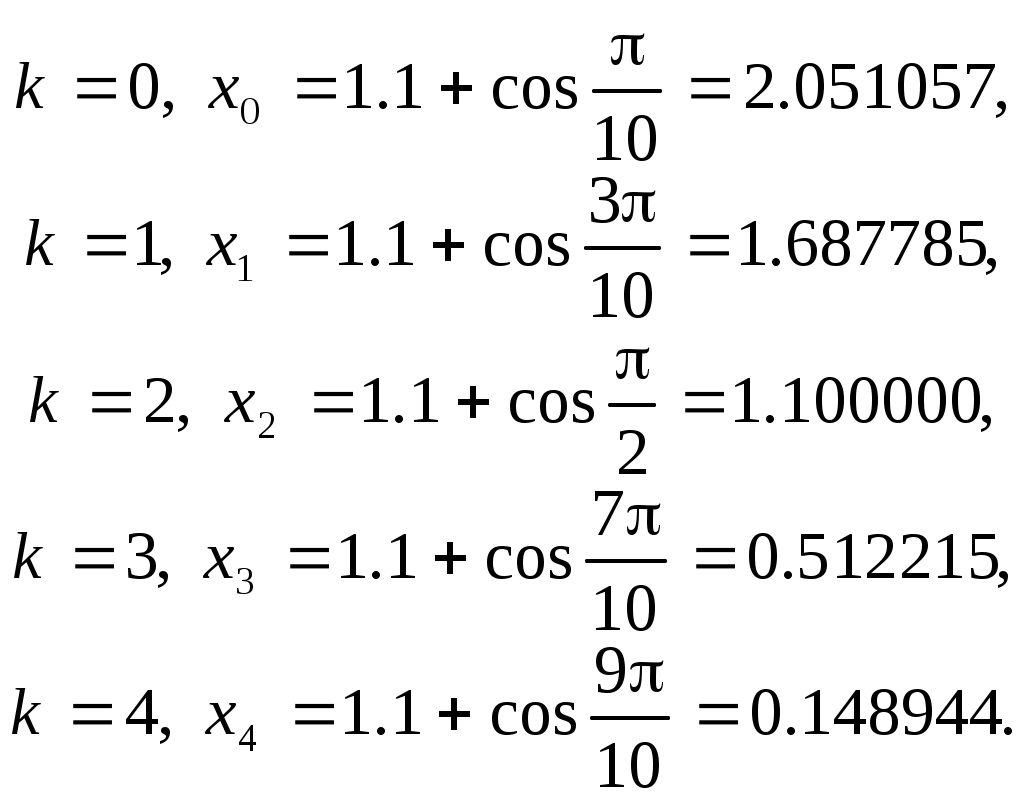 Согласно теории, в случае расположения узлов интерполяции в нулях многочлена Чебышева гарантирована минимальная погрешность интерполяции, равная Построим для случаев (а) и (б) таблицы разделенных разностей. (а)
(б)
Вычисления по этим таблицам дают: (а) 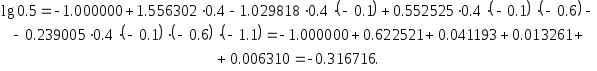 (б) 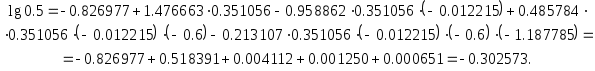 Истинное значение Так как таблица разностей очень короткая, а 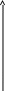  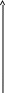 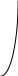                 0.1 2.1 0.1 0.6 1.1 1.6 2.1 функции 1 Иорген Педерсен Грам (1850-1916 ) - датский математик. Карл Вейерштрасс (1815-1897) – немецкий математик. Карл Давид Тольме Рунге (1856-1927) - немецкий физик и математик. Жорж Фабер (1877-1966) - швейцарский математик. Пафнутий Львович Чебышев (1821-1894) – русский математик и механик. Анри Леон Лебег (1875-1941) - французский математик. 1 Родриг; Бенжамен Оленд Родригес (1794-1851) - французский математик и экономист. 1 Жан Батист Жозеф Фурье (1768-1830) - французский математик. |
