|
|
методичка по КП. 3. Метод наименьших квадратов и специальные интерполяционные многочлены
Помимо погрешности от приближенной замены 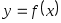 на на 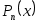 возникает еще дополнительная погрешность, связанная с тем, что значения интерполируемой функции тоже задаются с погрешностью. Пусть заданные в узлах возникает еще дополнительная погрешность, связанная с тем, что значения интерполируемой функции тоже задаются с погрешностью. Пусть заданные в узлах 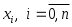 значения значения 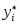 содержат погрешности содержат погрешности 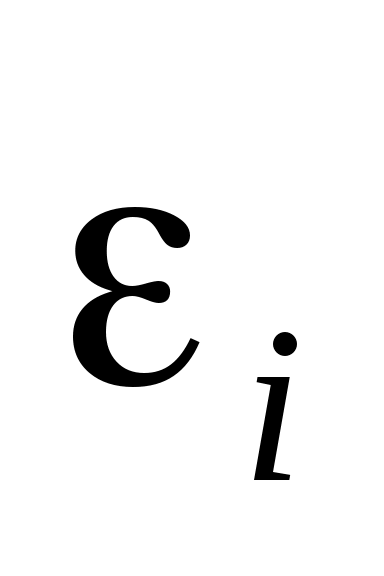 . Тогда . Тогда 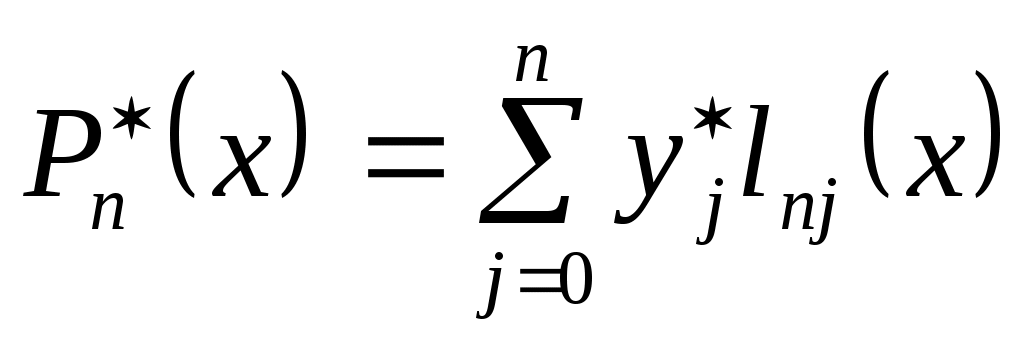 содержат погрешность содержат погрешность 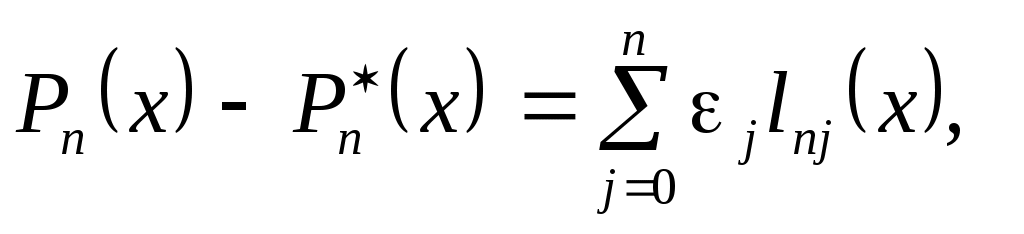 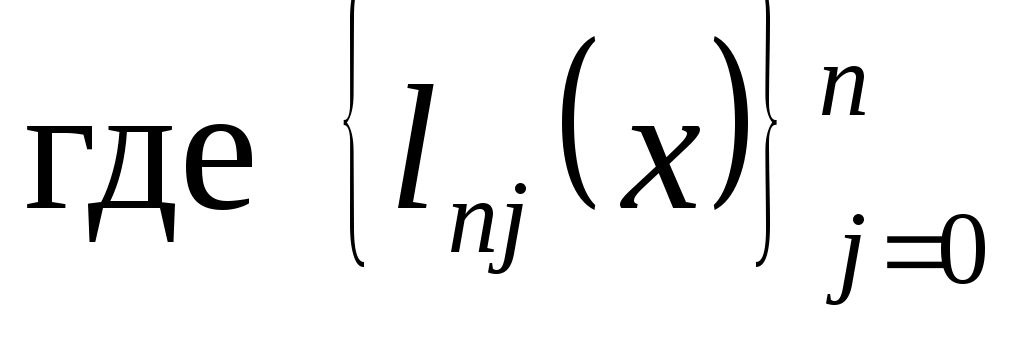 - Лагранжев базис. - Лагранжев базис.
Пусть известно, что верхняя граница погрешности 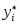 равна равна 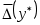 , то есть , то есть 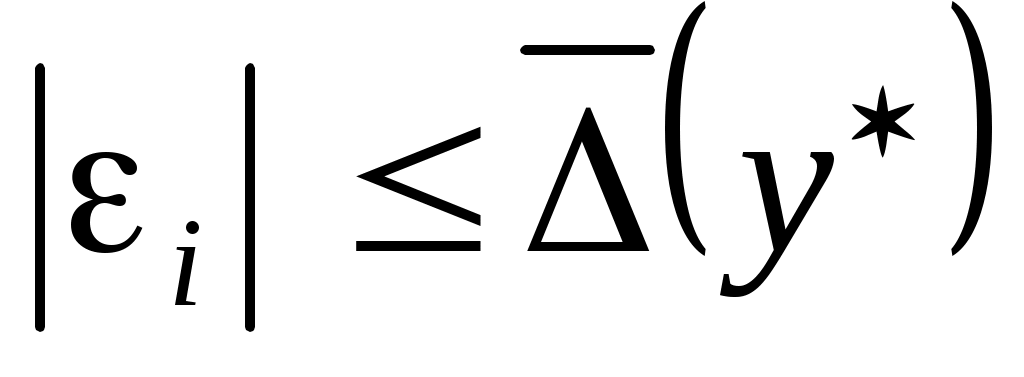 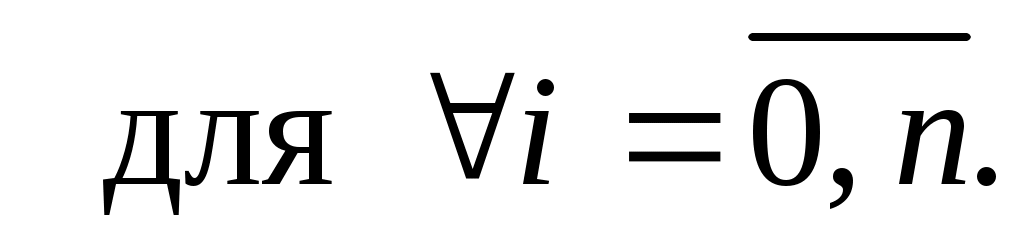 Тогда для верхней границы соответствующей погрешности многочлена Тогда для верхней границы соответствующей погрешности многочлена 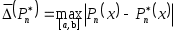 справедлива оценка справедлива оценка
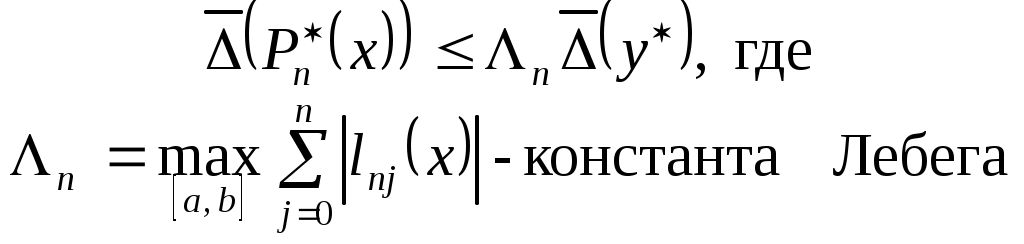 . (3.4.1) . (3.4.1)
В задаче интерполирования константа Лебега играет роль абсолютного числа обусловленности, то есть в самом неблагоприятном случае погрешность входных данных при интерполяции может возрасти в 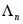 раз. Величина раз. Величина 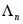 зависит от расположения узлов интерполяции. Например, если в качестве узлов интерполяции взяты нули многочленов Чебышева, то зависит от расположения узлов интерполяции. Например, если в качестве узлов интерполяции взяты нули многочленов Чебышева, то
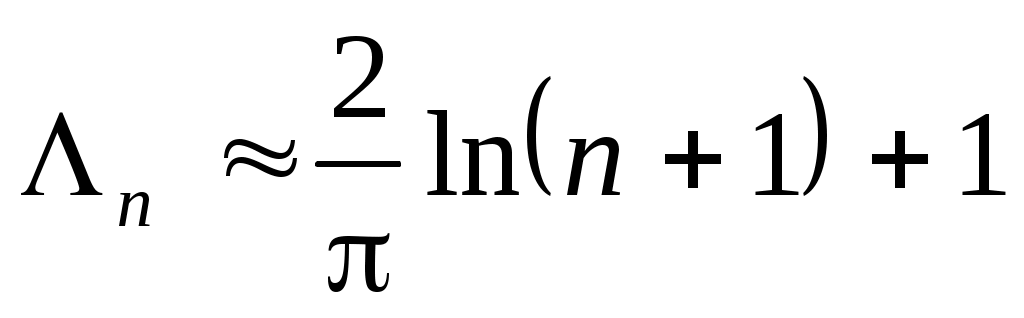 . (3.4.2) . (3.4.2)
Если же узлы равноотстоящие, то 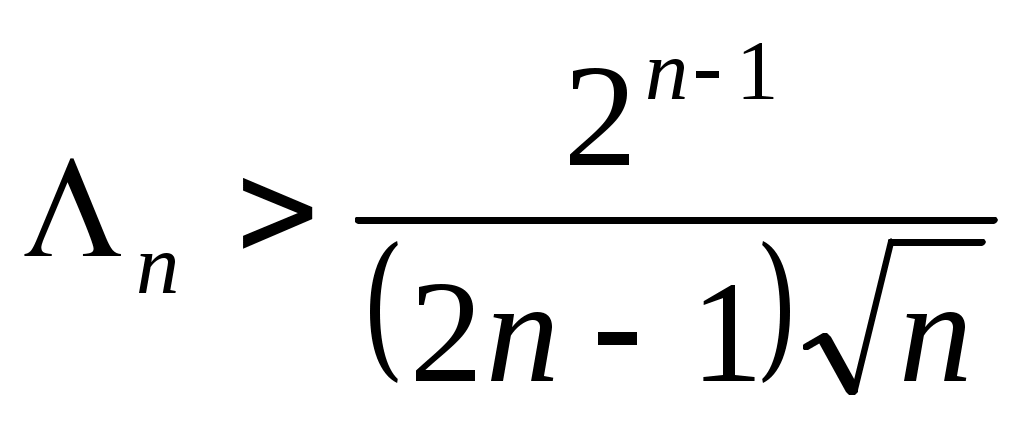 и уже при и уже при 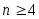 обусловленность задачи резко ухудшается. Из этого следует важный практический вывод: в вычисленияхне следует использовать интерполяционные многочлены высокой степени с равноотстоящими узлами. обусловленность задачи резко ухудшается. Из этого следует важный практический вывод: в вычисленияхне следует использовать интерполяционные многочлены высокой степени с равноотстоящими узлами.
3.5. Многочлены Чебышева
Система функций 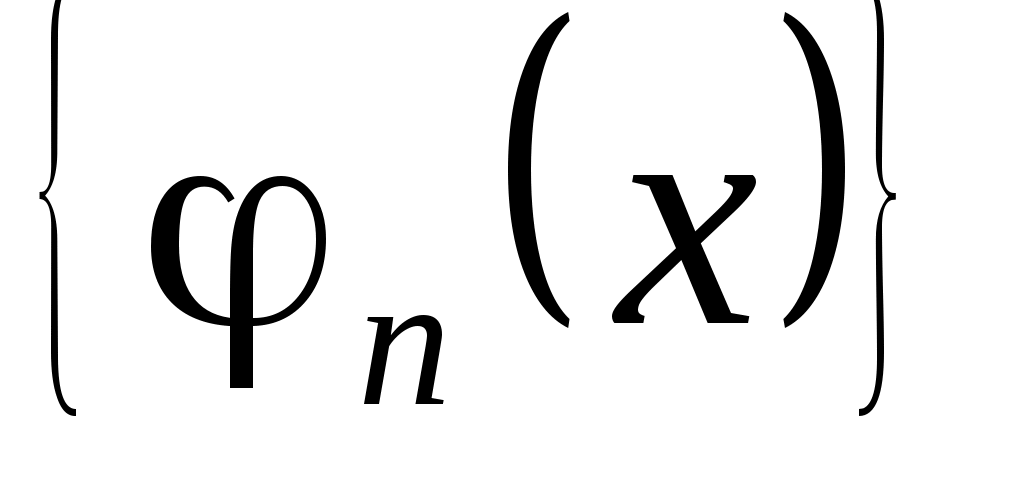 , заданных на , заданных на 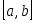 , называется ортогональной на , называется ортогональной на 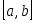 , если , если
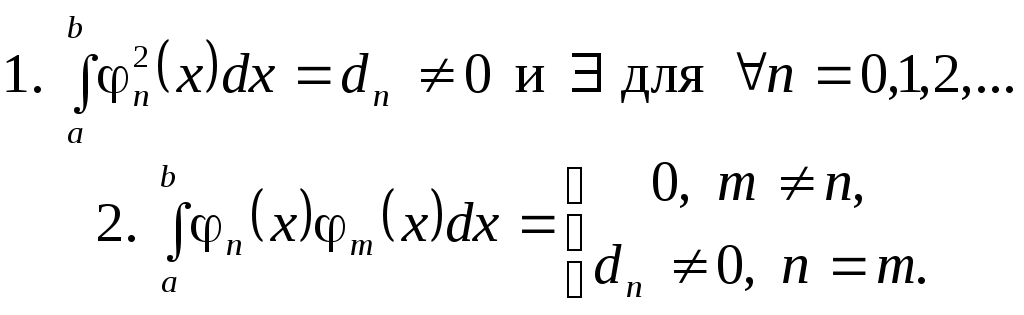 (3.5.1) (3.5.1)
Система функций 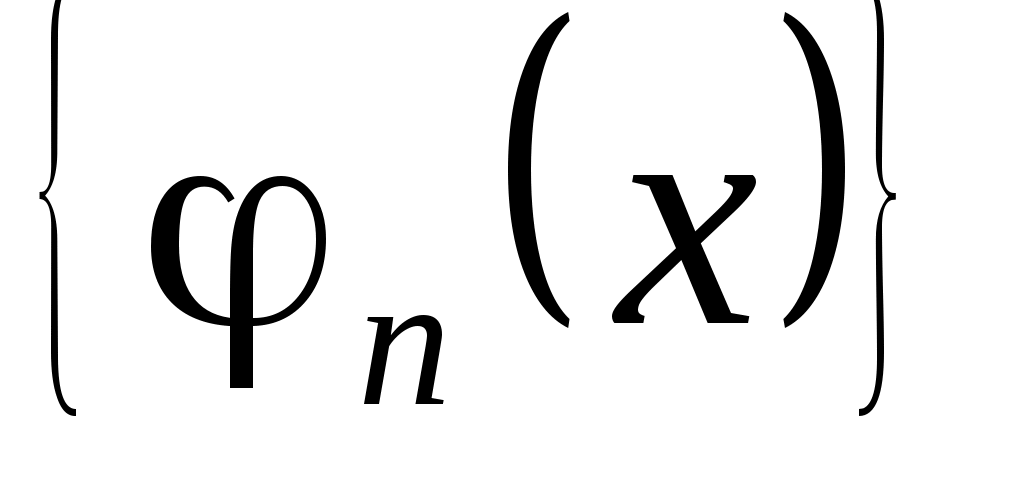 , заданных на , заданных на 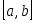 , называется ортогональной на , называется ортогональной на 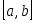 с весом с весом 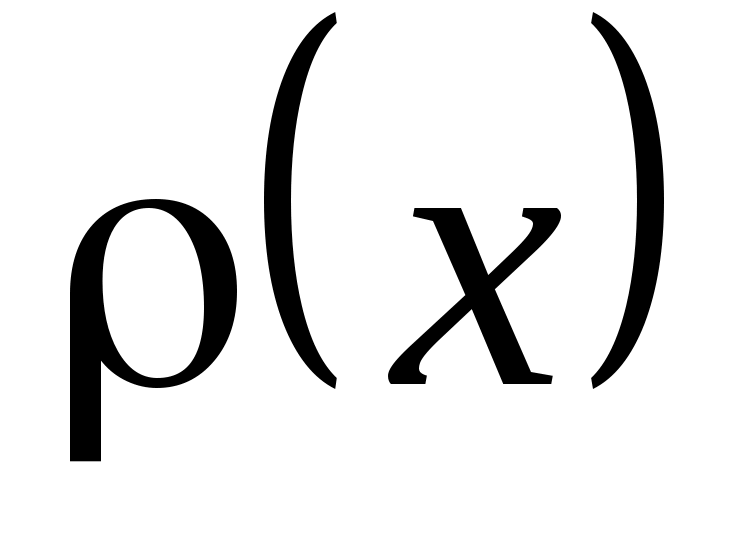 , если , если
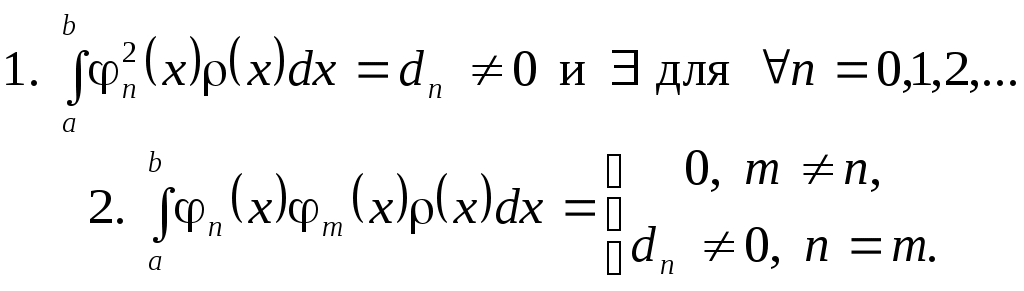 (3.5.2) (3.5.2)
Функция 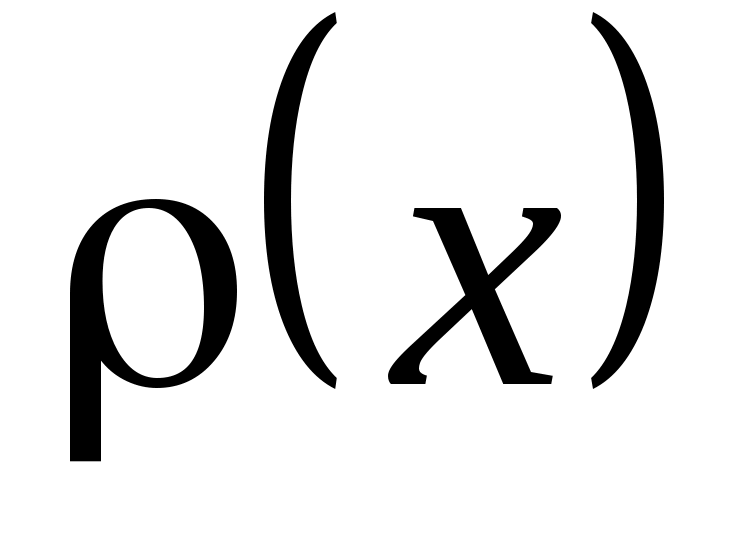 называется весовой функцией для системы называется весовой функцией для системы 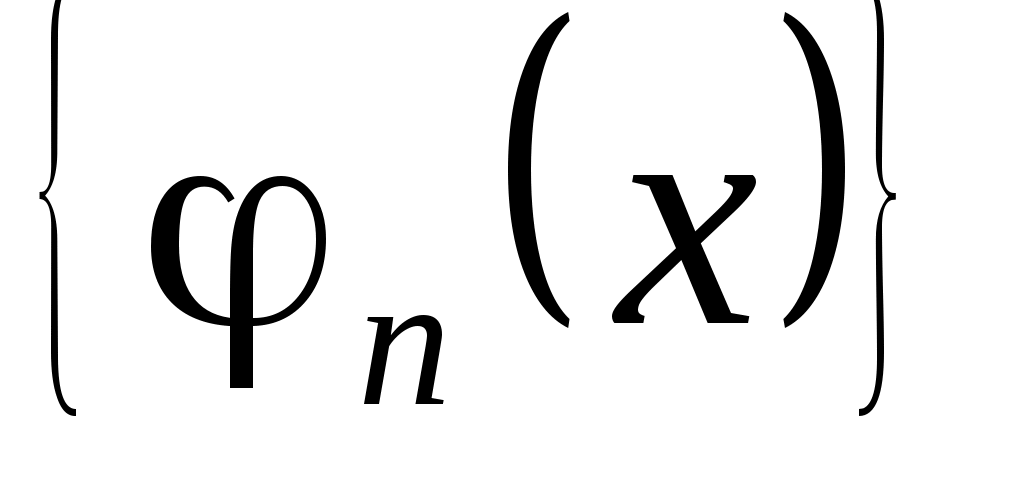 . Если . Если 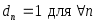 , то система функций , то система функций 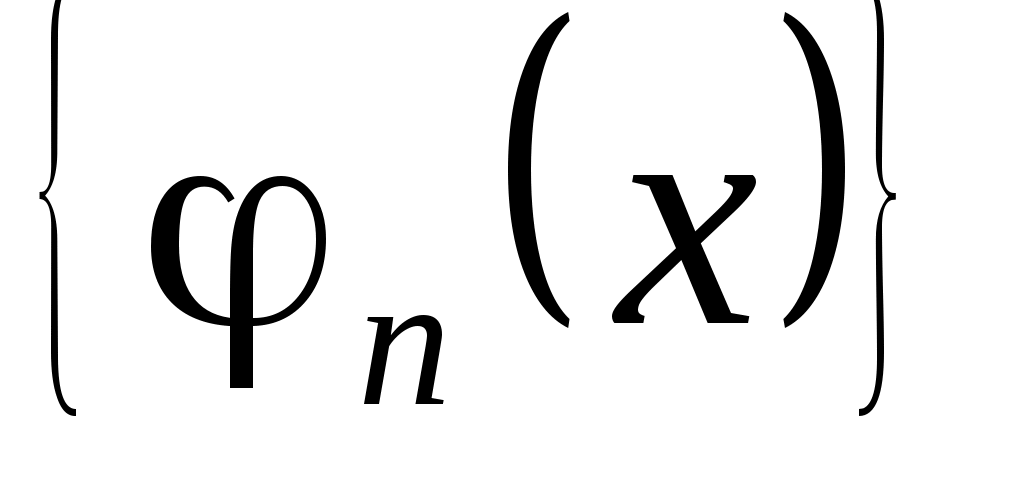 называется ортонормированной. называется ортонормированной.
В качестве примера системы функций, ортогональной с весом, приведем многочлены Чебышева, которые известны еще и тем, что являются полиномами, наименее уклоняющимися от нуля. Эти многочлены определяют разными способами. Например:
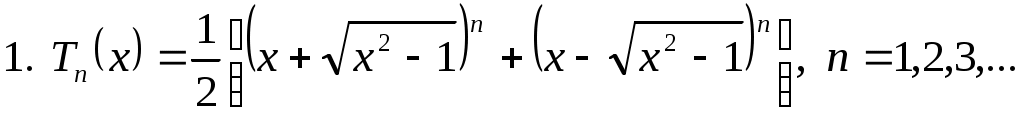 (3.5.3) (3.5.3)
2. Являются решениями следующего дифференциального уравнения:
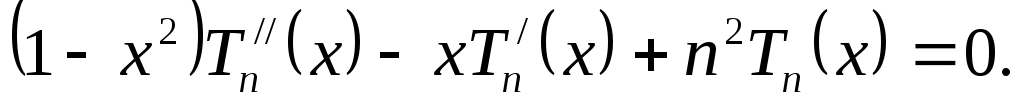 (3.5.4) (3.5.4)
3. Определяются из формулы Родрига1
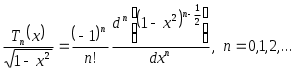 (3.5.5) (3.5.5)
4. Определяются рекуррентно:
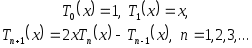 (3.5.6) (3.5.6)
Иногда в качестве полиномов Чебышева берут функции 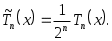
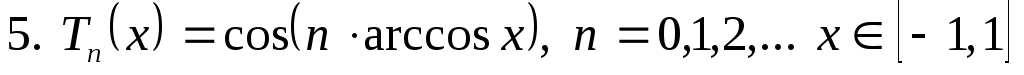 . (3.5.7) . (3.5.7)
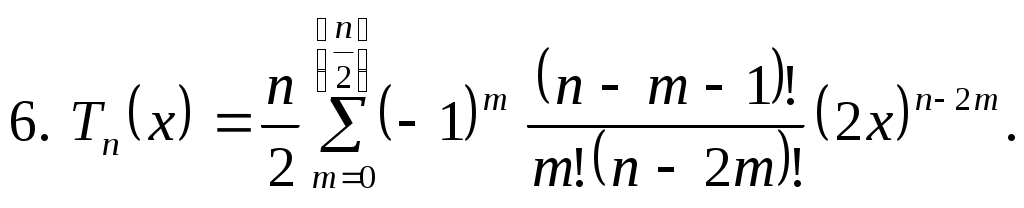 (3.5.8) (3.5.8)
Многочлены Чебышева обладают множеством замечательных свойств.
Теорема 3.4. Полиномы Чебышева 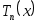 образуют на отрезке образуют на отрезке 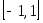 ортогональную систему с весом ортогональную систему с весом 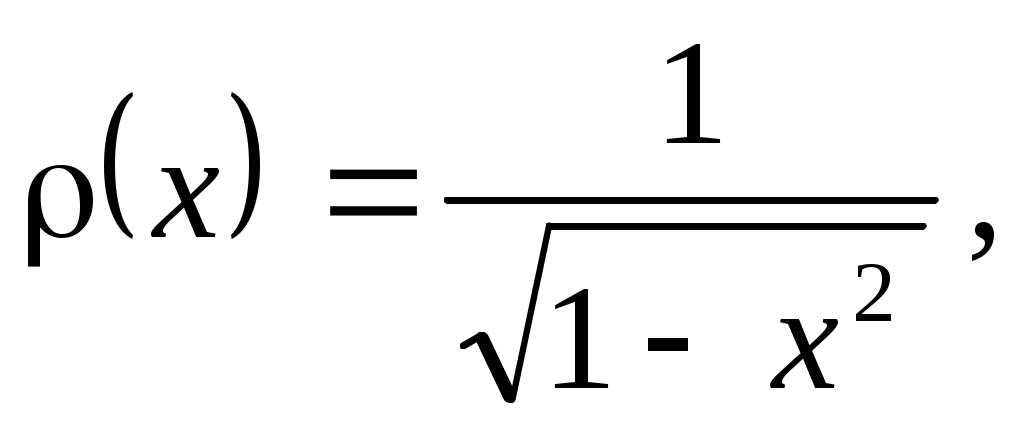 то есть то есть
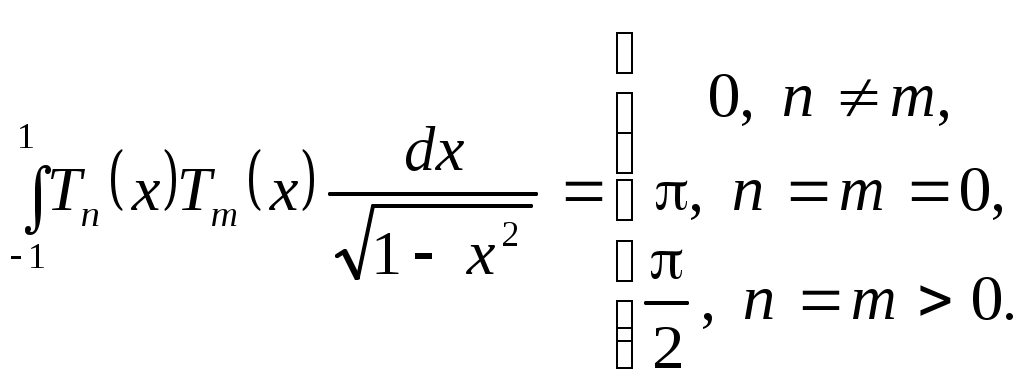 (3.5.9) (3.5.9)
Действительно, 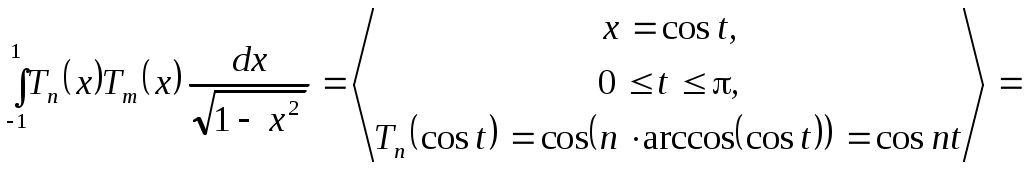
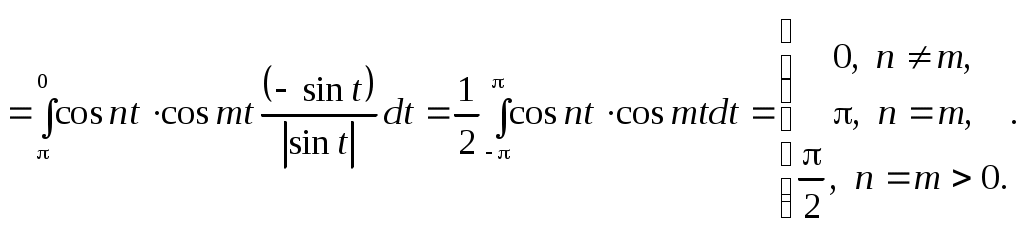
     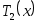 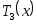 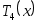 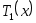 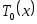
           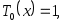
1 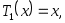
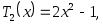
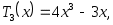
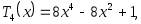
  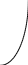  -1 1 -1 1 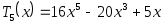
и так далее.
-1
Теорема 3.5. При четном 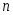 многочлен многочлен 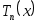 содержит только четные степени содержит только четные степени 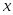 и является четной функцией, а при нечетном и является четной функцией, а при нечетном 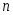 многочлен многочлен 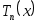 содержит только нечетные степени содержит только нечетные степени 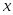 и является нечетной функцией. и является нечетной функцией.
Теорема 3.6. При 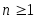 старший коэффициент многочлена старший коэффициент многочлена 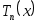 равен равен 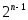 , то есть , то есть 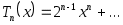
Теорема 3.7. При 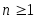 многочлен многочлен 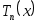 имеет ровно имеет ровно 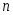 действительных корней, расположенных на отрезке действительных корней, расположенных на отрезке 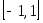 и вычисляемых по формуле и вычисляемых по формуле
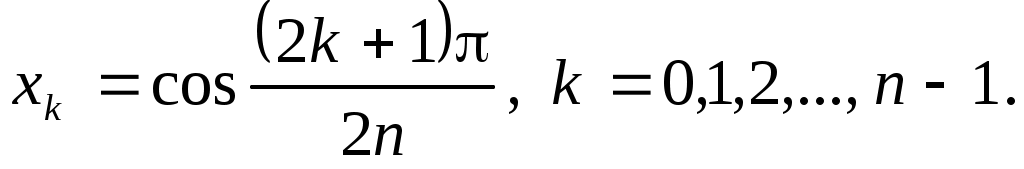 (3.5.10) (3.5.10)
Теорема 3.8. При 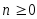 справедливо равенство справедливо равенство 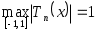 . Если . Если 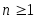 , то этот максимум достигается ровно в , то этот максимум достигается ровно в 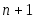 точках, которые находятся по формуле точках, которые находятся по формуле
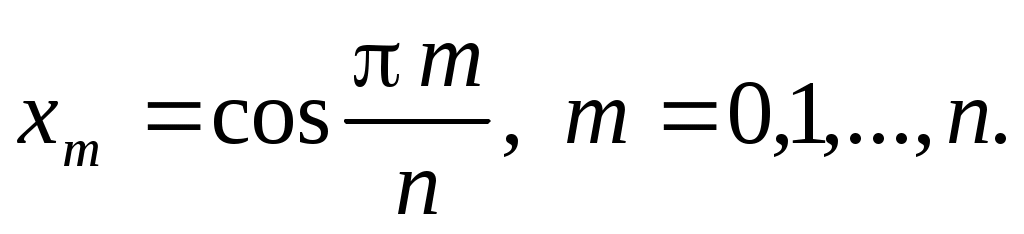 (3.5.11) (3.5.11)
При этом 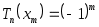 , то есть максимумы и минимумы многочлена Чебышева чередуются. , то есть максимумы и минимумы многочлена Чебышева чередуются.
Теоремы 3.7 и 3.8 легко доказываются с помощью формулы (3.5.7).
Назовем величину 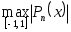 уклонением многочлена уклонением многочлена 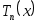 от нуля. Тогда справедлива следующая, доказанная П.Л. Чебышевым в 1854 г. теорема. от нуля. Тогда справедлива следующая, доказанная П.Л. Чебышевым в 1854 г. теорема.
Теорема 3.9. Среди всех многочленов фиксированной степени 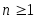 со старшим коэффициентом со старшим коэффициентом 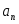 , равным единице, наименьшее уклонение от нуля, равное , равным единице, наименьшее уклонение от нуля, равное 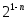 , имеет многочлен , имеет многочлен 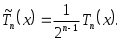
Последнее свойство имеет особую ценность для приложений. Действительно, тогда для любого многочлена 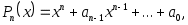 отличного от отличного от 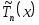 , справедливо неравенство , справедливо неравенство
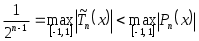 . (3.5.12) . (3.5.12)
В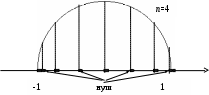 силу формул (3.5.10) и (3.5.11) нули и точки экстремума полинома силу формул (3.5.10) и (3.5.11) нули и точки экстремума полинома 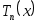 можно построить следующим образом: разделив полуокружность, опирающуюся на отрезок можно построить следующим образом: разделив полуокружность, опирающуюся на отрезок 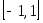 на на 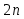 частей, спроецируем полученные точки на диаметр. Нумеруя проекции слева направо, получим, что все проекции с нечетными номерами являются нулями полинома частей, спроецируем полученные точки на диаметр. Нумеруя проекции слева направо, получим, что все проекции с нечетными номерами являются нулями полинома 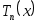 , а с четными – его точками экстремума. Из геометрических соображений вытекает, что как нули, так и точки экстремума полинома , а с четными – его точками экстремума. Из геометрических соображений вытекает, что как нули, так и точки экстремума полинома 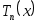 сгущаются к концам отрезка сгущаются к концам отрезка 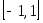 . .
|
|
|
 Скачать 2.21 Mb.
Скачать 2.21 Mb.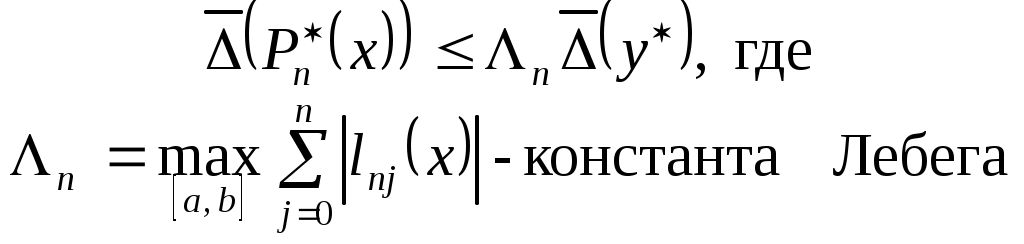 . (3.4.1)
. (3.4.1)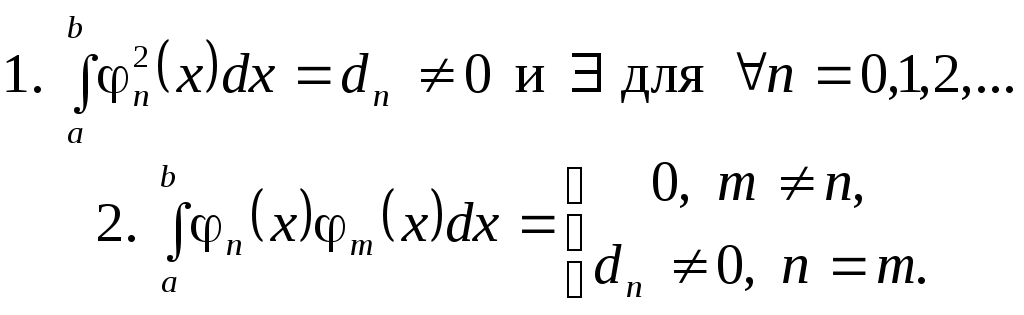 (3.5.1)
(3.5.1)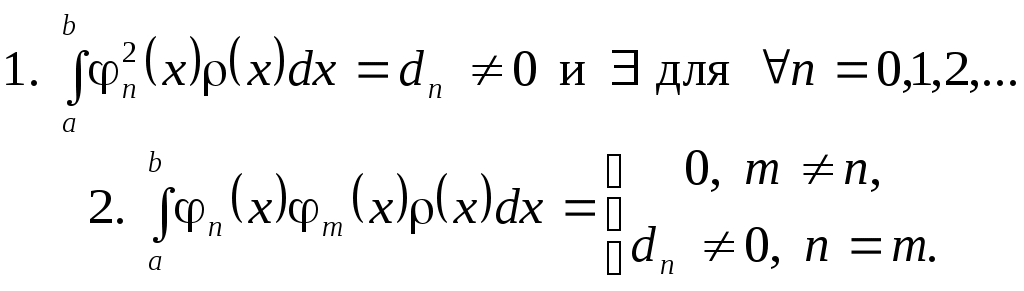 (3.5.2)
(3.5.2)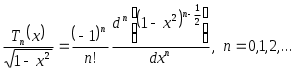 (3.5.5)
(3.5.5)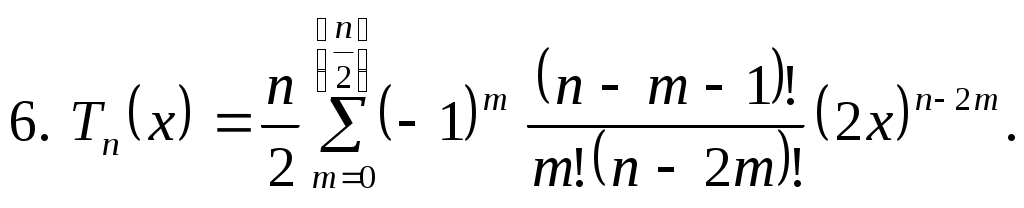 (3.5.8)
(3.5.8)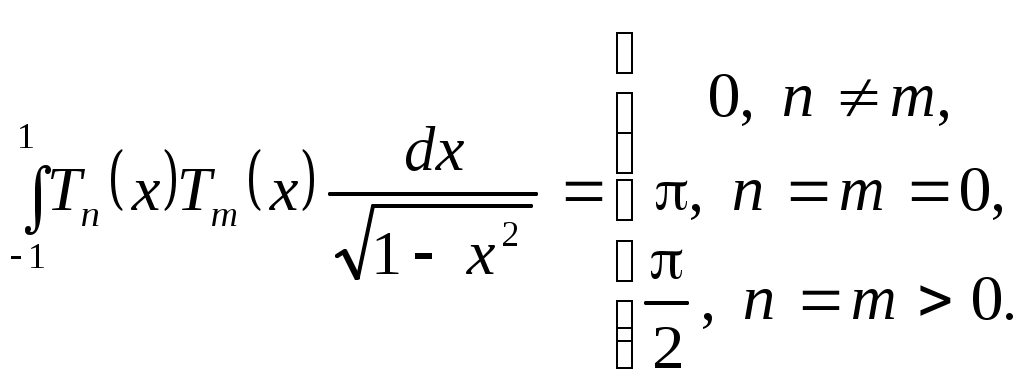 (3.5.9)
(3.5.9)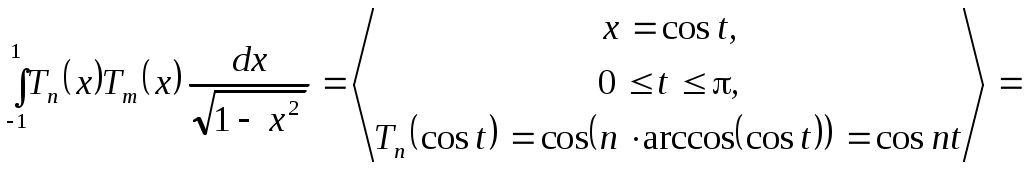
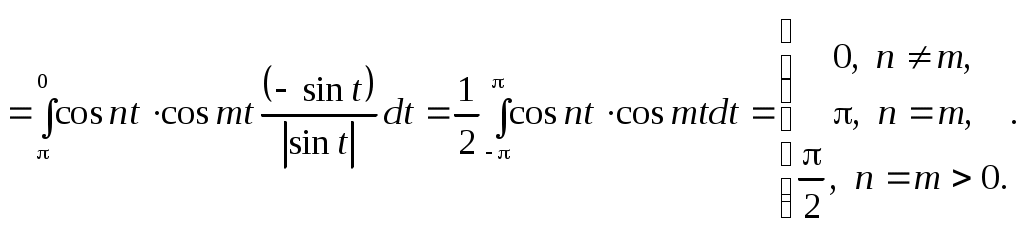







 -1 1
-1 1  силу формул (3.5.10) и (3.5.11) нули и точки экстремума полинома
силу формул (3.5.10) и (3.5.11) нули и точки экстремума полинома 