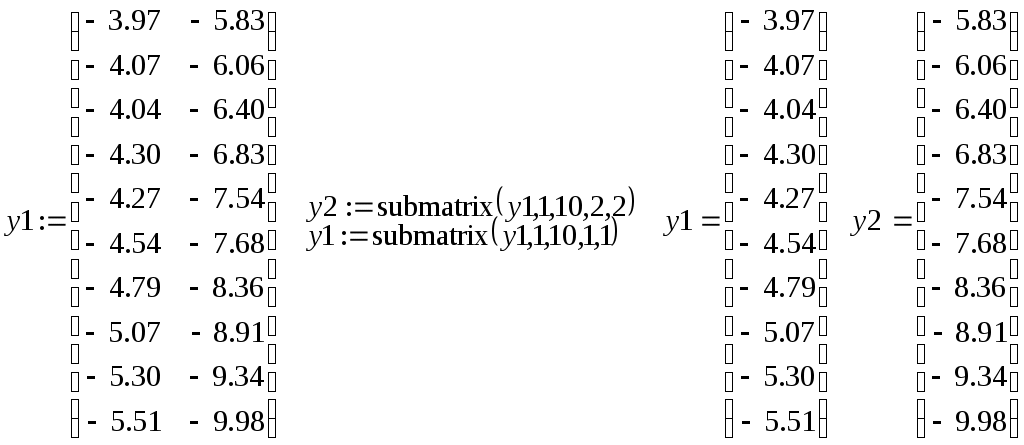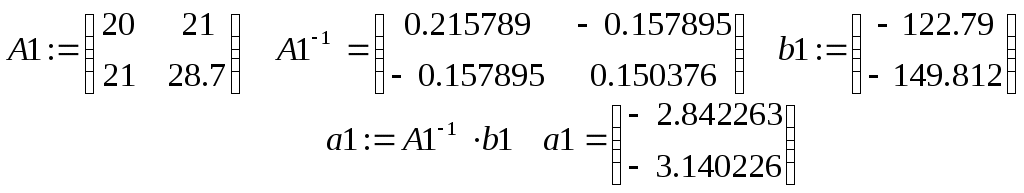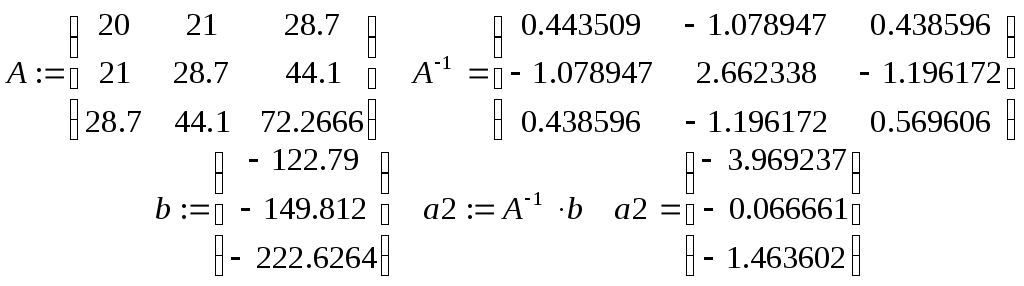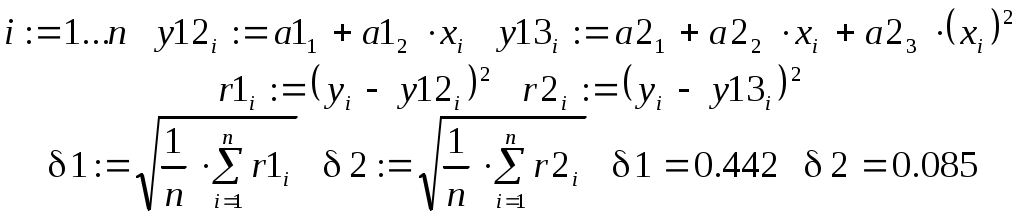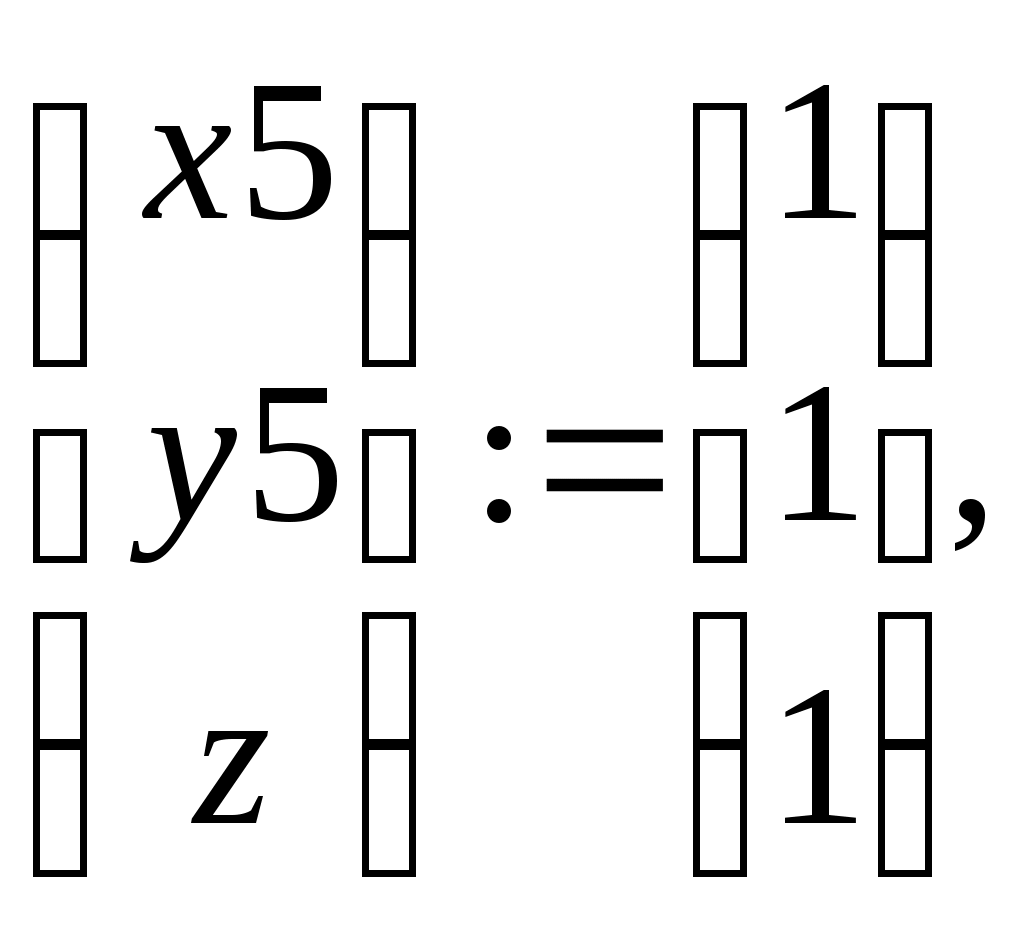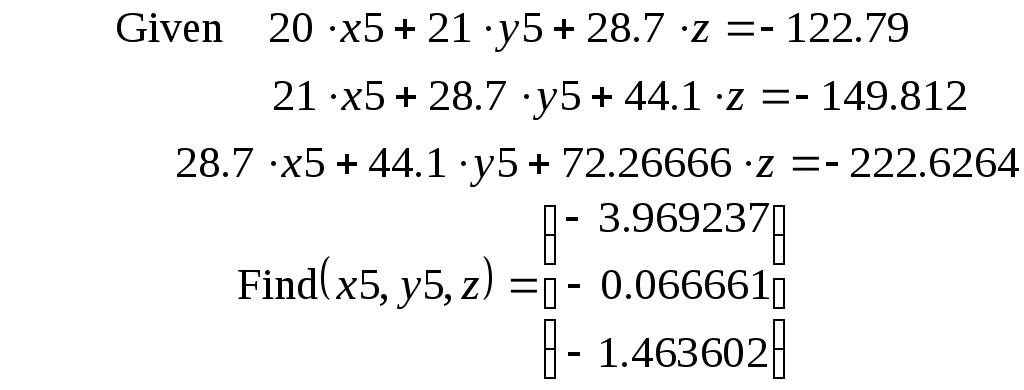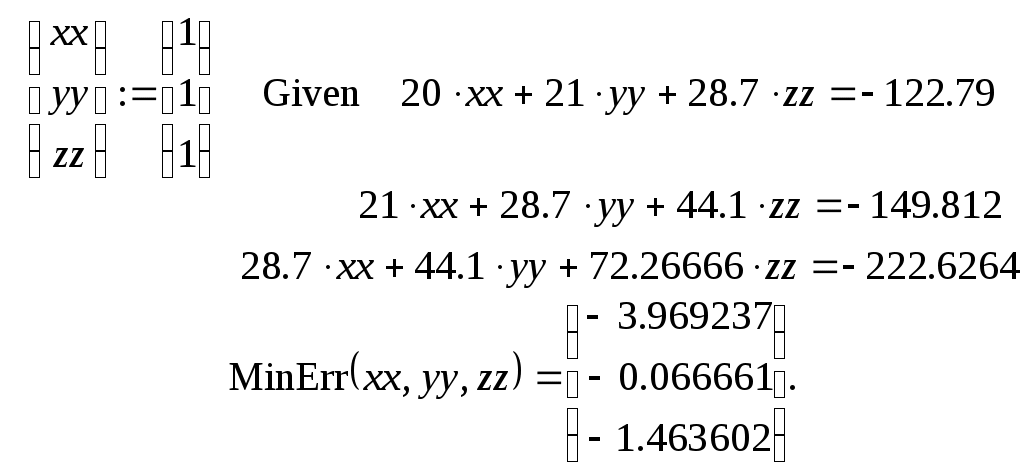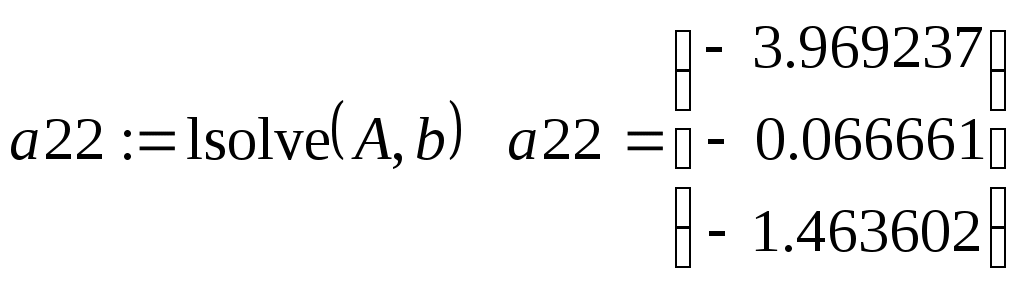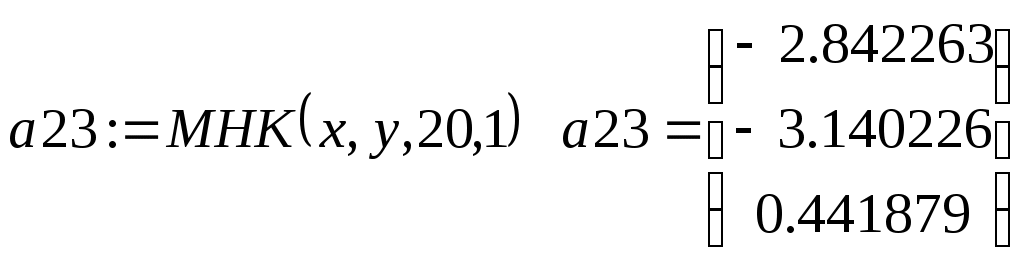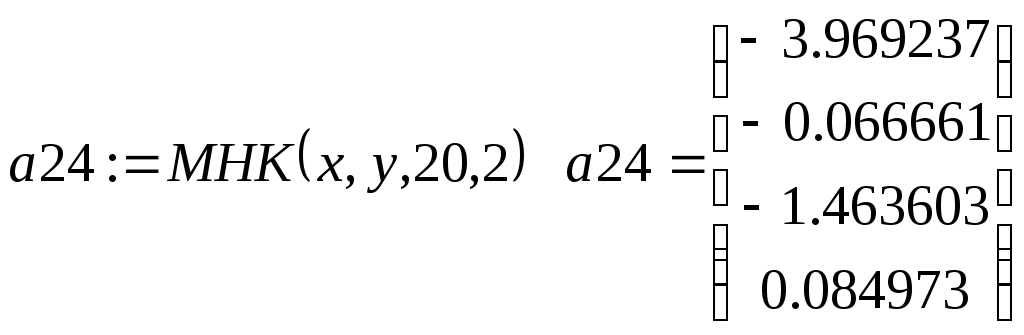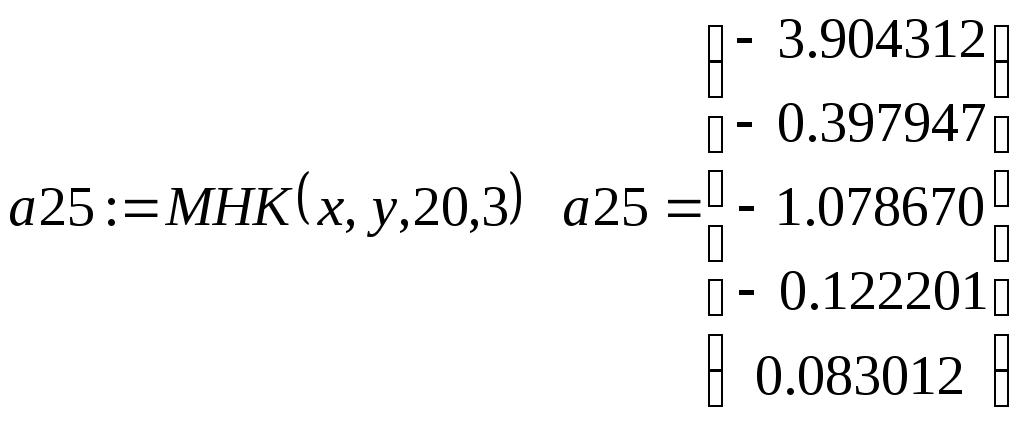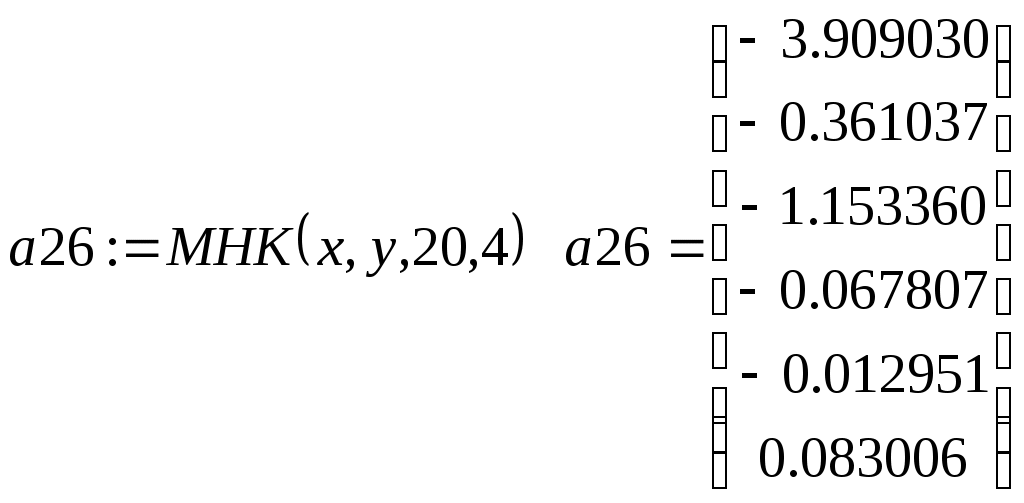|
|
методичка по КП. 3. Метод наименьших квадратов и специальные интерполяционные многочлены
Очень часто при анализе эмпирических данных необходимо найти явную функциональную зависимость между двумя величинами 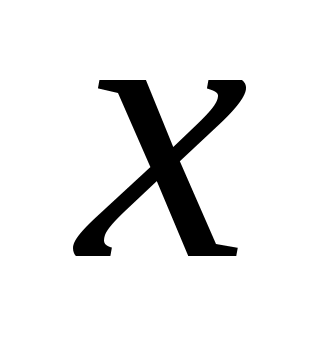 и и 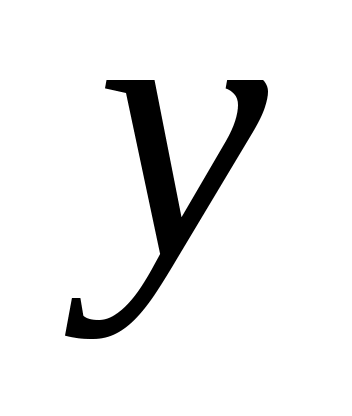 , полученными в результате измерений. Поскольку опытные данные всегда содержат ошибки, то строить интерполяционный многочлен , полученными в результате измерений. Поскольку опытные данные всегда содержат ошибки, то строить интерполяционный многочлен 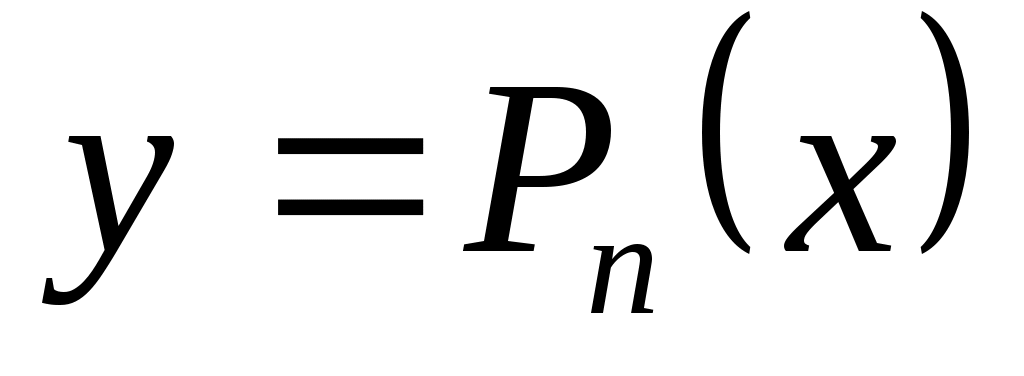 не рационально, так как при интерполяции ошибки повторяются. Желательно по возможности сгладить и минимизировать ошибки наблюдений. Этот результат достигается построением многочлена наилучшего среднего квадратического приближения по методу наименьших квадратов. не рационально, так как при интерполяции ошибки повторяются. Желательно по возможности сгладить и минимизировать ошибки наблюдений. Этот результат достигается построением многочлена наилучшего среднего квадратического приближения по методу наименьших квадратов.
Итак, если 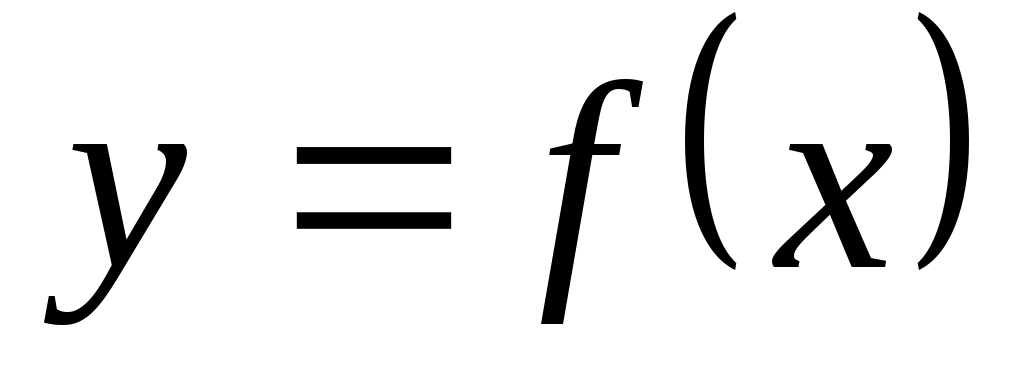 аппроксимируется многочленом вида аппроксимируется многочленом вида 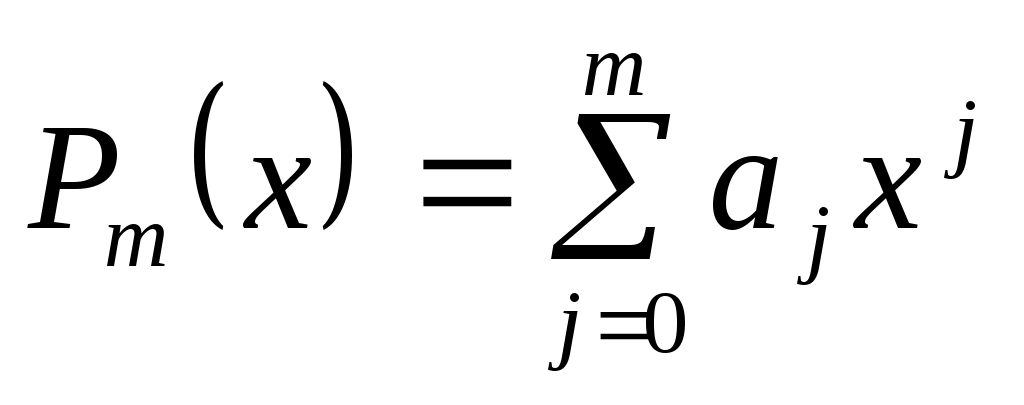 , так что система базисных функций имеет вид , так что система базисных функций имеет вид 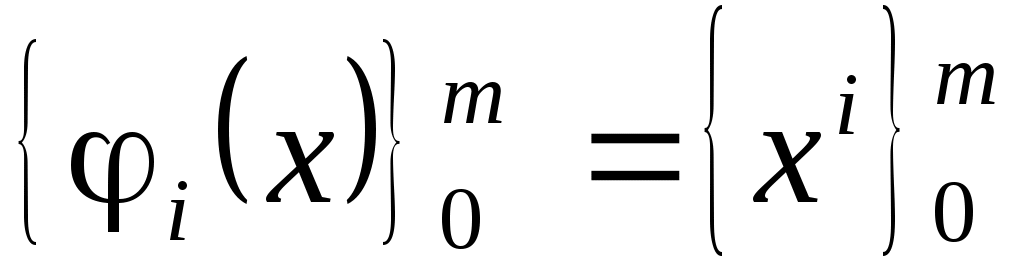 , то неизвестные коэффициенты многочлена , то неизвестные коэффициенты многочлена 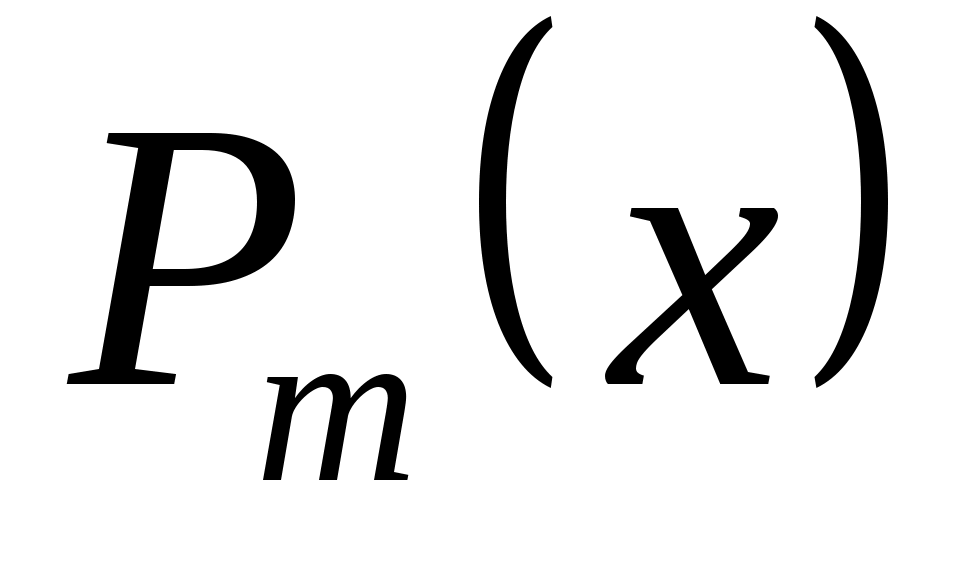 по методу наименьших квадратов определяются из решения системы (3.1.7). по методу наименьших квадратов определяются из решения системы (3.1.7).
В подразделе 3.1 описан пример «ручного» вычисления коэффициентов линейной и квадратичной модели по методу наименьших квадратов. Решим аналогичную задачу средствами пакета Mathcad различными способами. Сформируем вначале вектора исходных данных.
В алгебре матриц в среде Mathcad доступны несколько очень удобных встроенных функций, например, submatrix, stack и augment. Функция 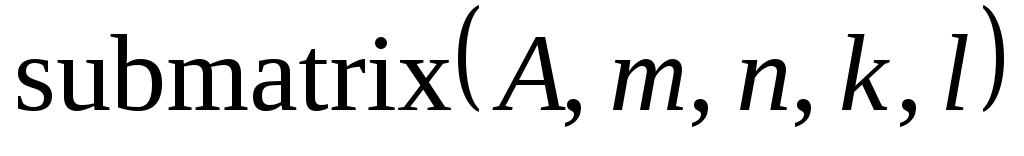 извлекает из матрицы извлекает из матрицы  подматрицу, содержащуюся в подматрицу, содержащуюся в  со строки со строки 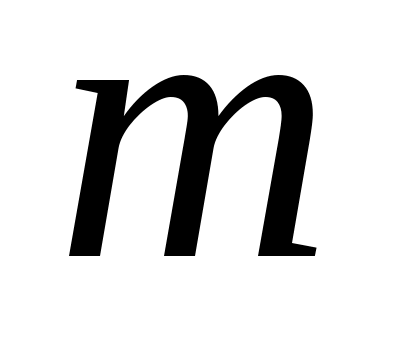 по строку по строку 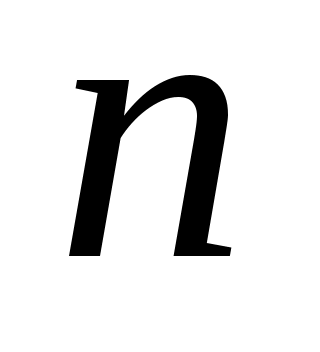 и со столбца с номером и со столбца с номером  по номер по номер 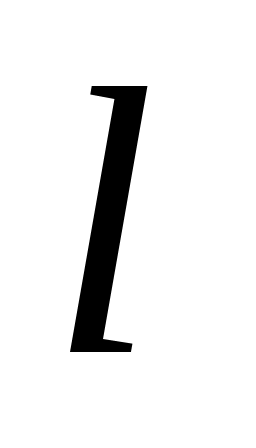 . Функции . Функции 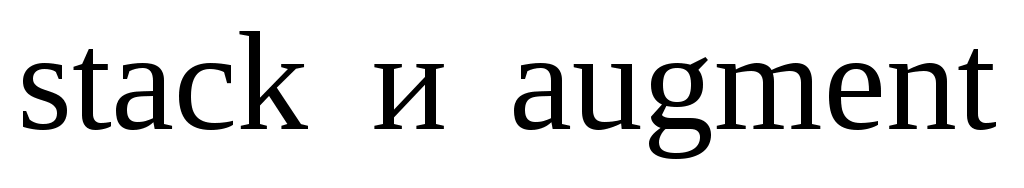 , наоборот, формируют одну матрицу из двух. После работы , наоборот, формируют одну матрицу из двух. После работы 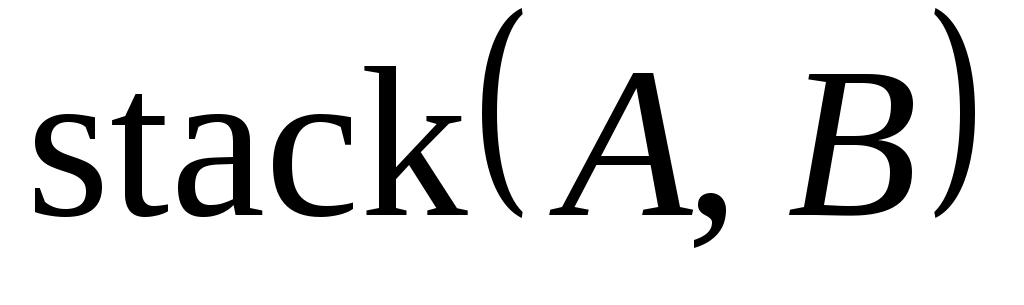 получается массив, сформированный расположением получается массив, сформированный расположением  над над 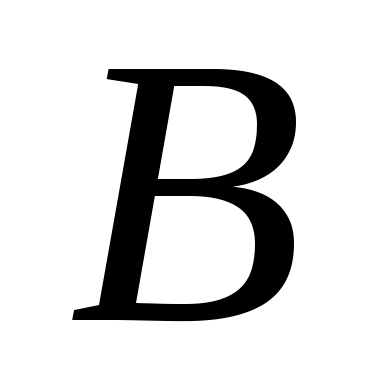 , при этом матрицы , при этом матрицы  и и 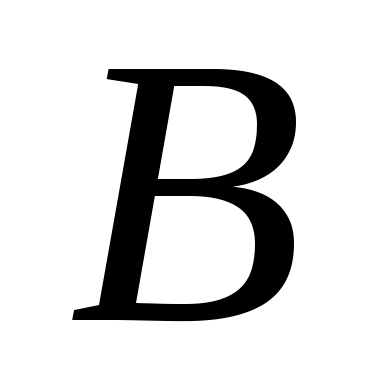 должны иметь одинаковое число столбцов. Функция должны иметь одинаковое число столбцов. Функция 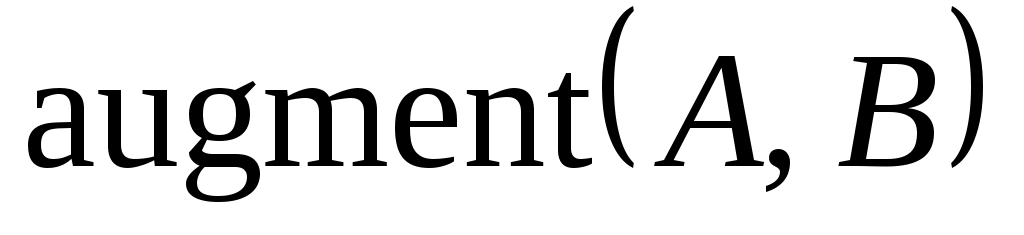 располагает матрицы располагает матрицы  и и  рядом, рядом,  справа от справа от  ; эти матрицы должны иметь одинаковое число строк. ; эти матрицы должны иметь одинаковое число строк.
Введем с клавиатуры
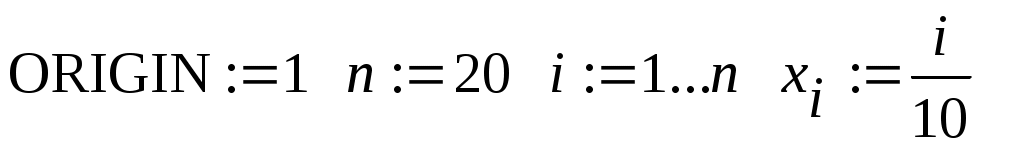
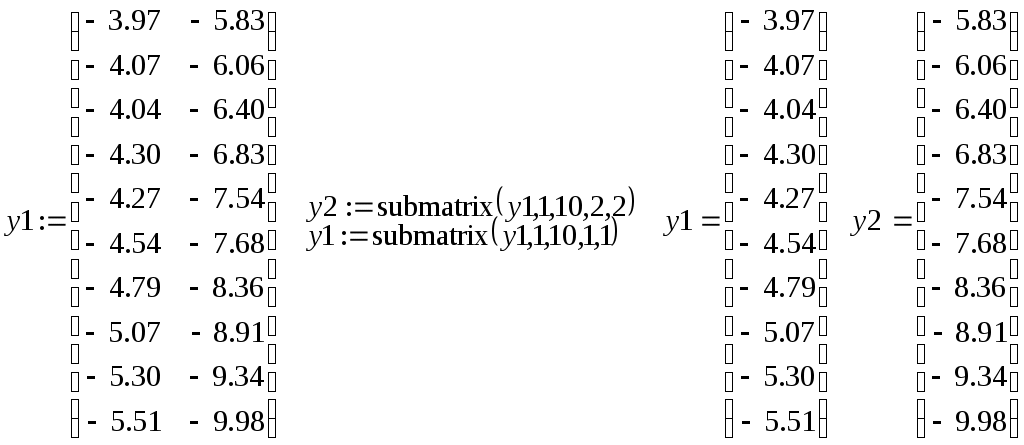

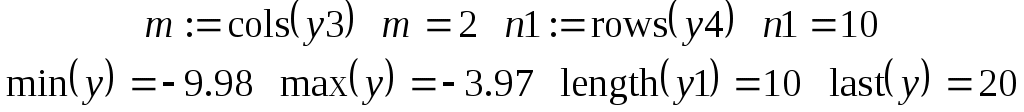
Функции 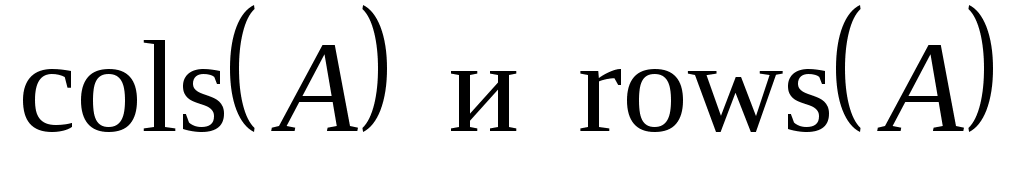 возвращают число столбцов и строк матрицы возвращают число столбцов и строк матрицы  , , 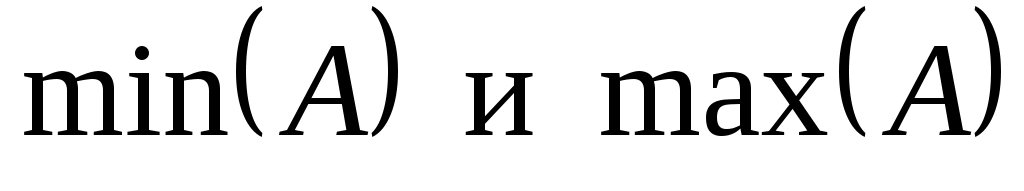 соответственно наименьшее и наибольшее значение элементов в соответственно наименьшее и наибольшее значение элементов в  , ,  - число элементов в векторе - число элементов в векторе 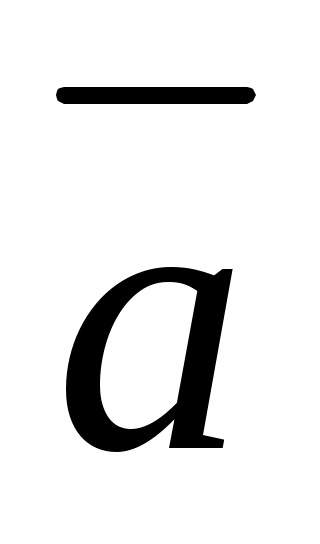 , , 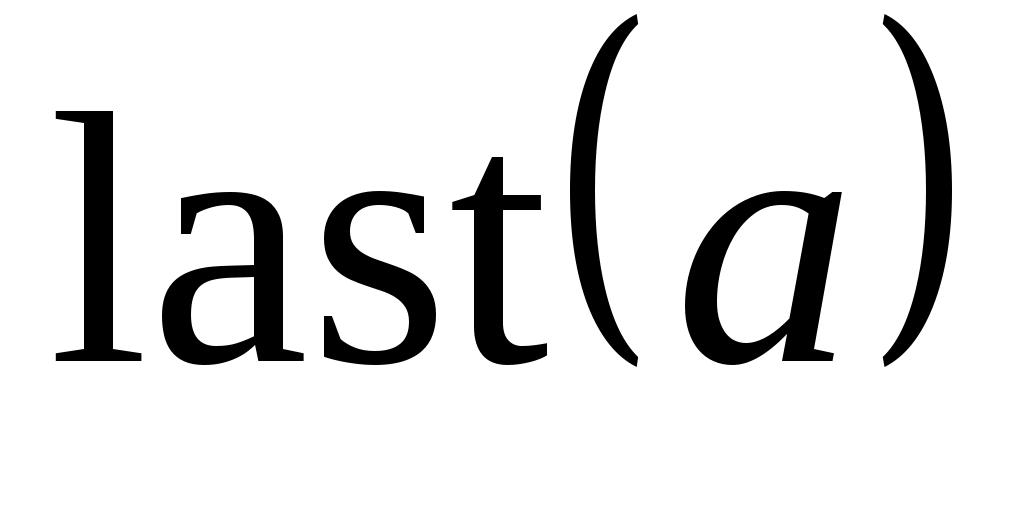 - индекс последнего элемента в векторе - индекс последнего элемента в векторе 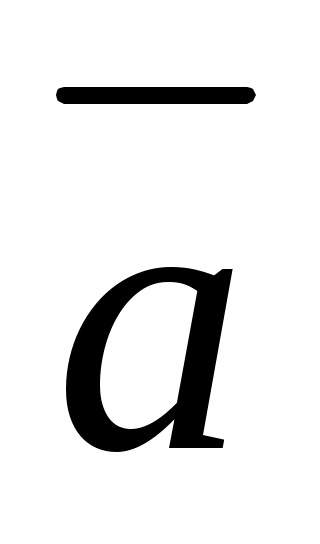 с учетом значения переменной с учетом значения переменной  . .
Построим линейную и квадратичную модель по формулам (3.1.8) и (3.1.9). Для этого вычислим следующие величины. Введем еще одну предопределенную переменную пакета Mathcad 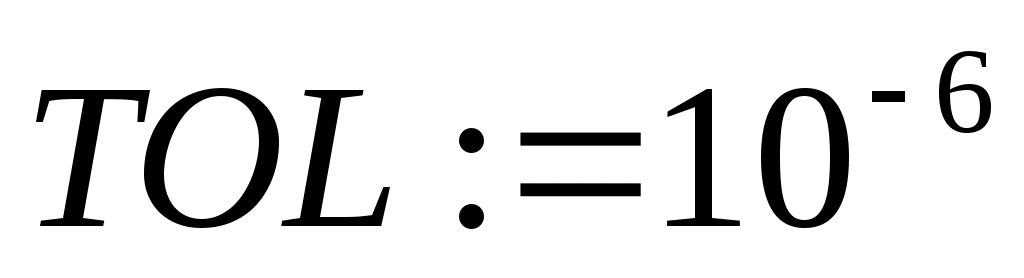 . Она определяет допустимую погрешность для различных алгоритмов аппроксимации, интегрирования, решения уравнений и так далее. По умолчанию . Она определяет допустимую погрешность для различных алгоритмов аппроксимации, интегрирования, решения уравнений и так далее. По умолчанию 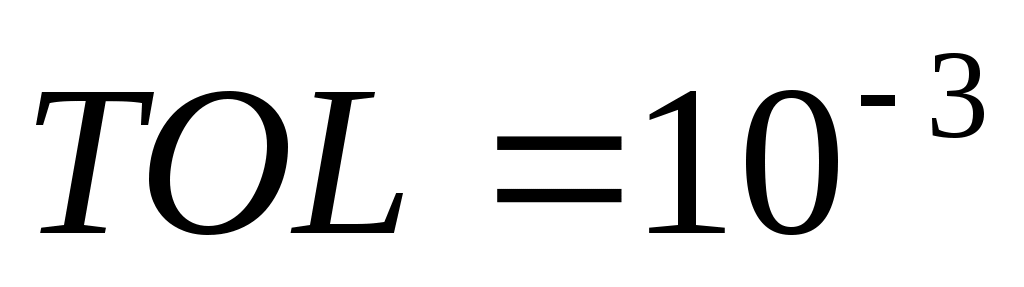 . Вычислим следующие величины: . Вычислим следующие величины:
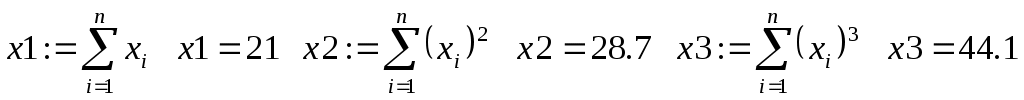
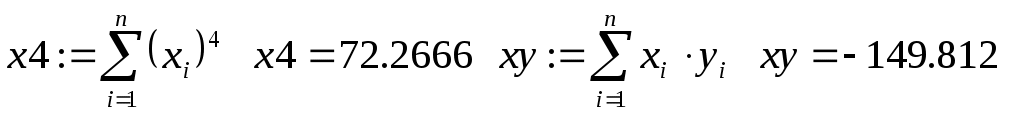
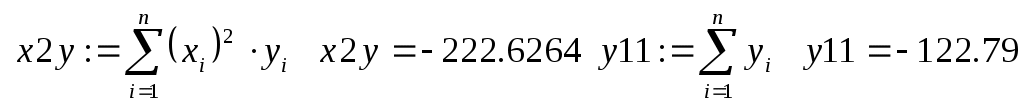
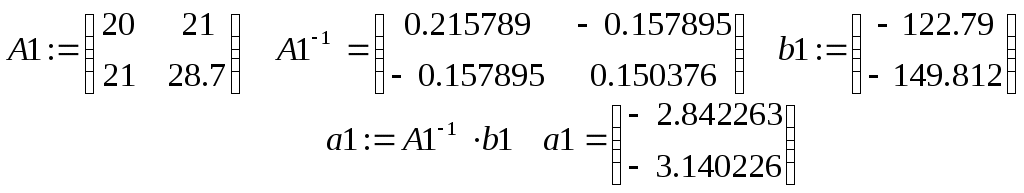
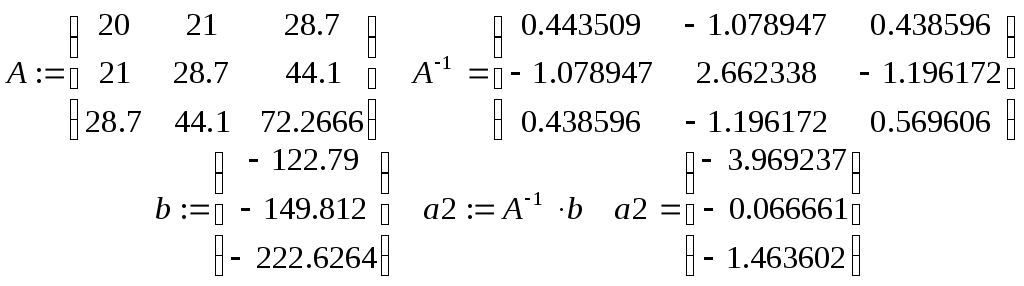
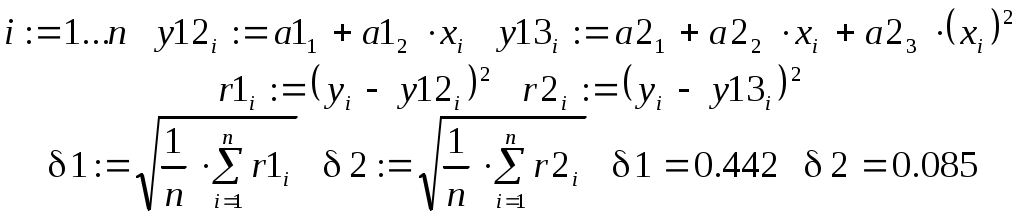
Коэффициенты системы нормальных уравнений линейной модели, то есть системы (3.1.8), находятся в матрице  , коэффициенты квадратичной модели (3.1.9) - в матрице , коэффициенты квадратичной модели (3.1.9) - в матрице  . Решение обеих систем линейных уравнений произведено с помощью обратной матрицы. Вектор . Решение обеих систем линейных уравнений произведено с помощью обратной матрицы. Вектор  содержит коэффициенты линейной модели, вектор содержит коэффициенты линейной модели, вектор 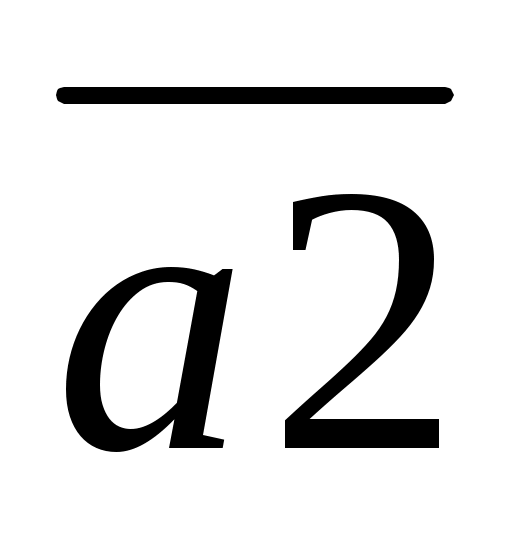 - квадратичной. - квадратичной.
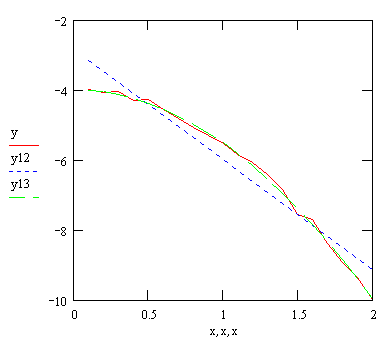
Далее вычисляются невязки по обеим моделям и находятся средние квадратические ошибки 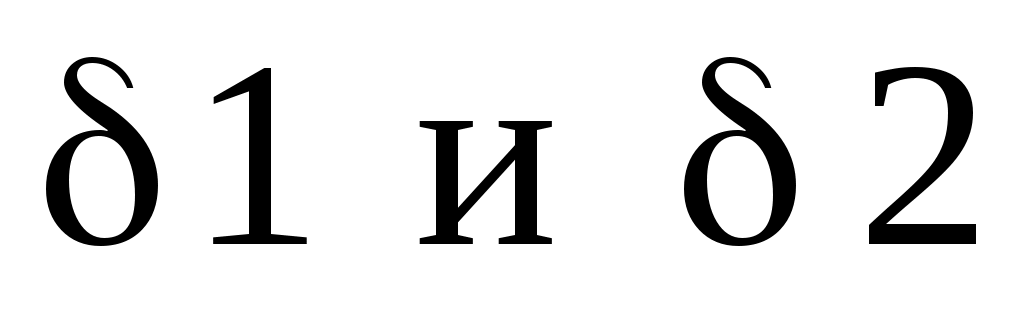 . Видно, что исходным данным хорошо удовлетворяет квадратичная модель . Видно, что исходным данным хорошо удовлетворяет квадратичная модель 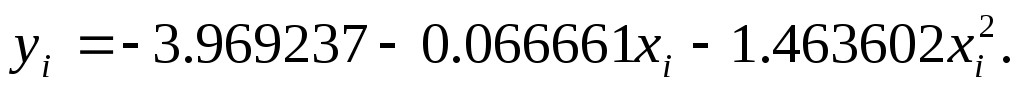 Этот факт отчетливо виден и на приведенном графике. Этот факт отчетливо виден и на приведенном графике.
Mathcad не назывался бы математическим пакетом, если бы не умел решать алгебраические системы различными, в том числе и более эффективными способами. Одним из таких способов является конструкция Given – Find. Это две команды: Given (Дано) и Find (Найти). Сначала задается какое-нибудь начальное приближение, например, для квадратичной модели
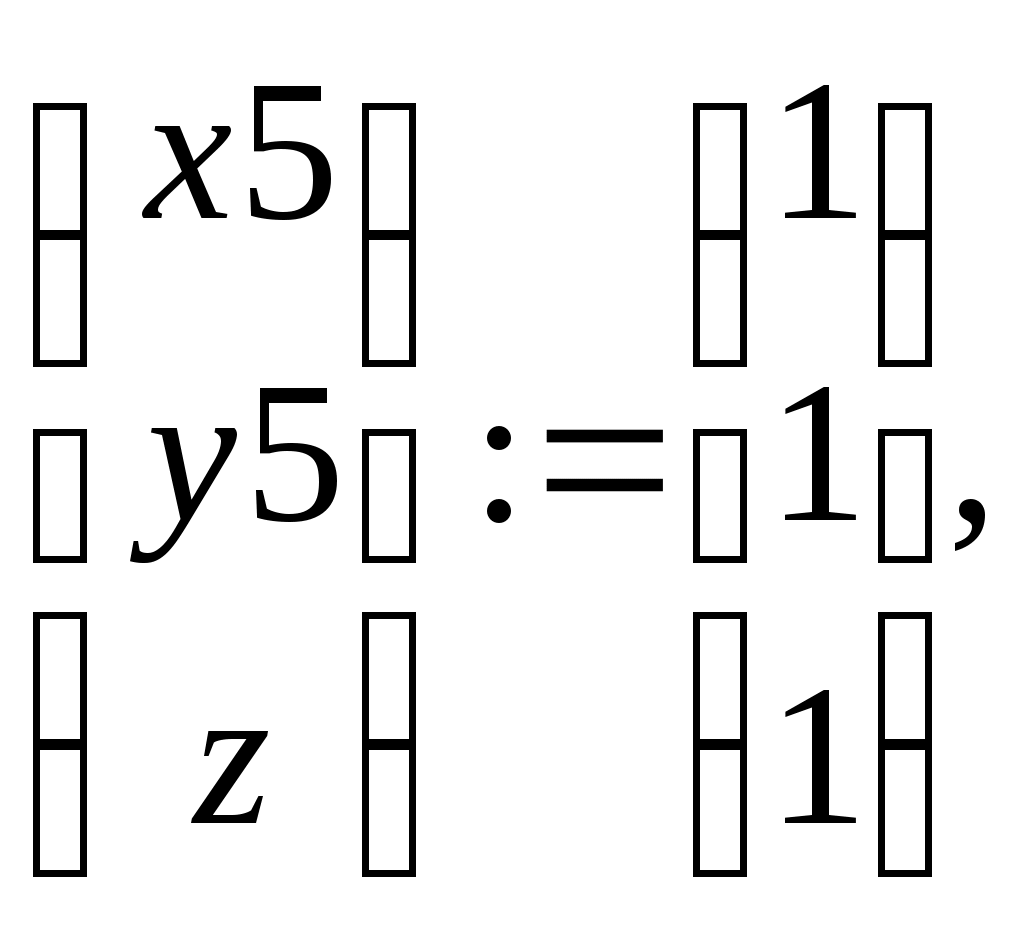
затем за ключевым словом Given нужно записать анализируемую систему, связывая левые и правые части уравнений знаком «эквивалентно» (жирным знаком «равно» из панели равенств и отношений или же нажимая сразу обе клавиши  ), после этого должно идти второе ключевое слово Find. Эта функция возвращает решение анализируемой системы: ), после этого должно идти второе ключевое слово Find. Эта функция возвращает решение анализируемой системы:
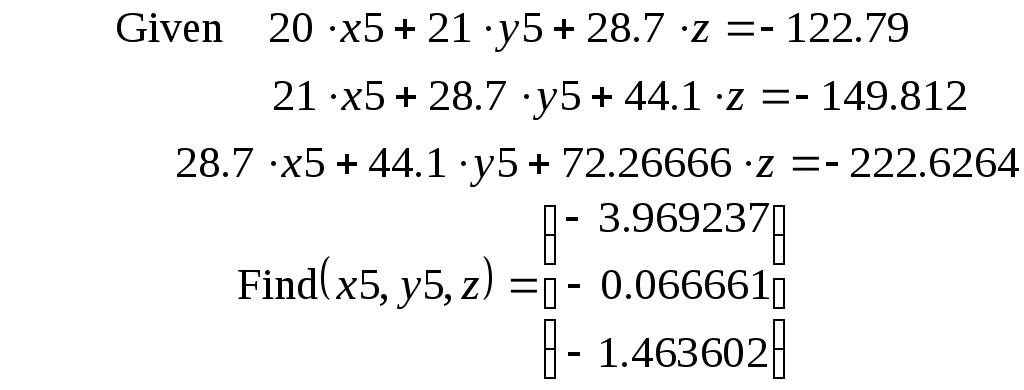
Неудобство применения пары Given – Find в том, что решаемая система уравнений должна быть записана в скалярной форме. Вместо функции Find можно использовать пару Given – MinErr. Функция 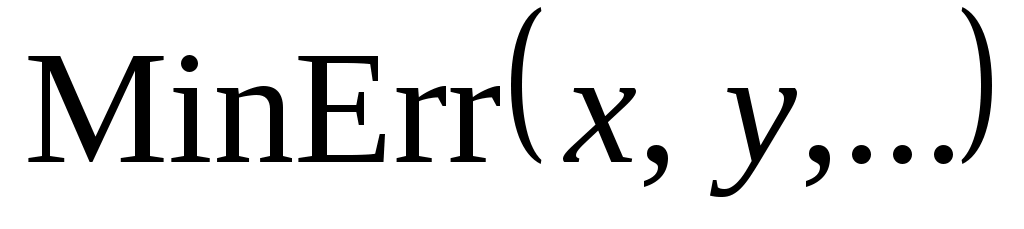 дает решение системы уравнений, которое приводит к минимальным невязкам. Число неизвестных системы должно быть равно числу аргументов функции MinErr. В нашем случае дает решение системы уравнений, которое приводит к минимальным невязкам. Число неизвестных системы должно быть равно числу аргументов функции MinErr. В нашем случае
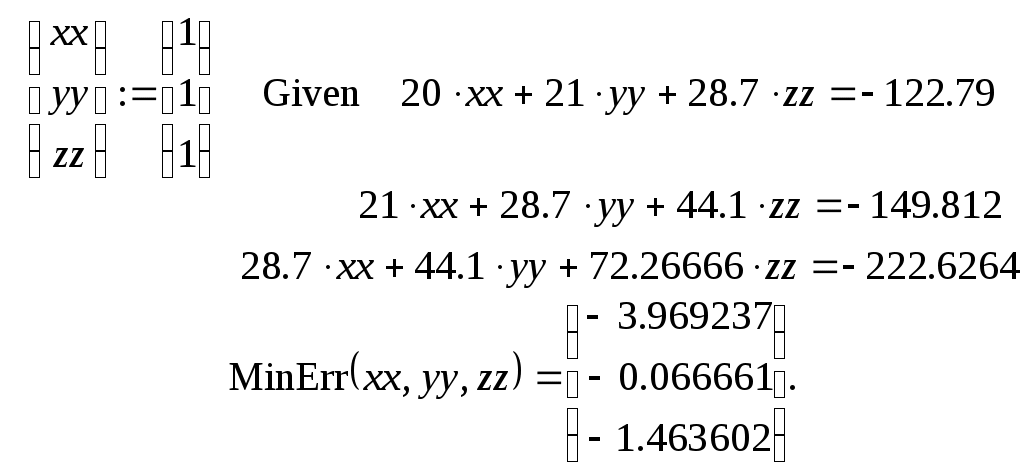
Наконец, для решения линейных систем алгебраических уравнений можно использовать встроенную функцию lsolve. Она возвращает вектор решения системы, записанной в матричном виде:
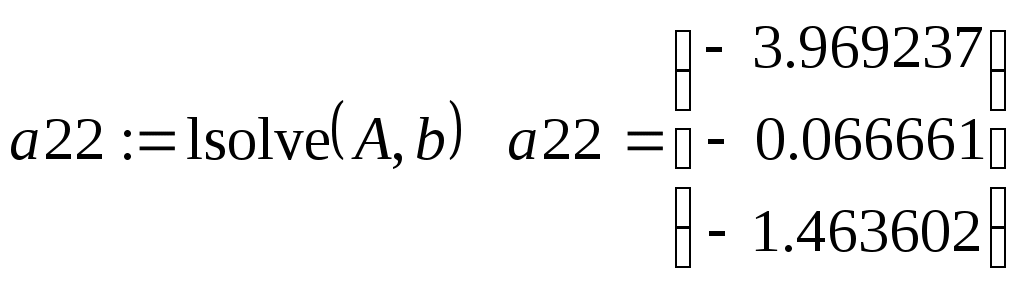
Заметим, что функцию lsolve можно использовать в программируемых конструкциях, тогда как пары Given – Find и Given – MinErr этого не допускают.
Приведем в заключение подпрограмму, реализующую вычисления по формуле (3.1.7) в общем случае коэффициентов сглаживающего многочлена заданной степени. Все операторы этой подпрограммы легко отождествляются с той или иной частью формулы (3.1.7). Параметры подпрограммы: 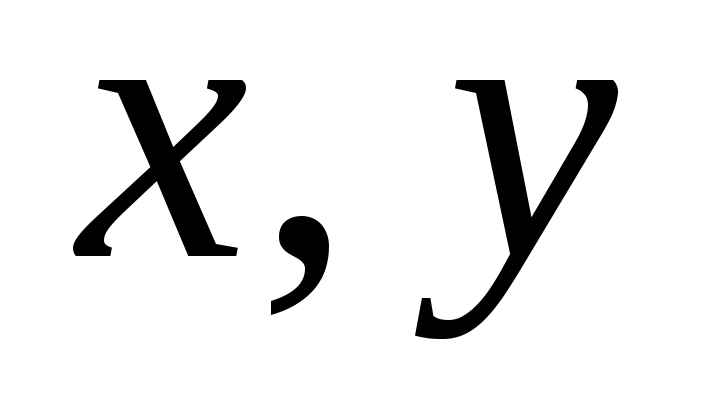 - вектора исходных данных, - вектора исходных данных, 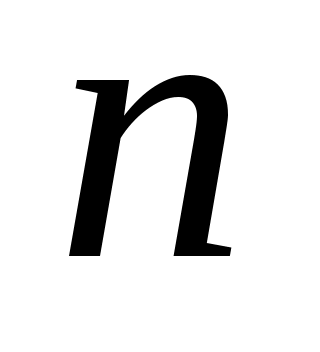 - число точек сетки таблично заданной функции, - число точек сетки таблично заданной функции, 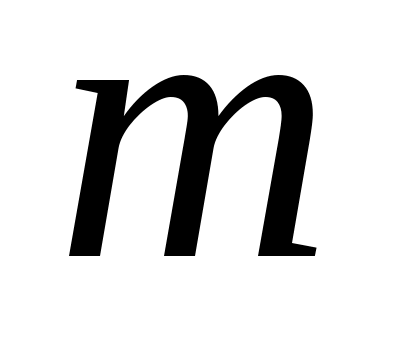 - требуемая степень сглаживающего многочлена. В результате работы подпрограмма МНК выдает вектор коэффициентов многочлена - требуемая степень сглаживающего многочлена. В результате работы подпрограмма МНК выдает вектор коэффициентов многочлена 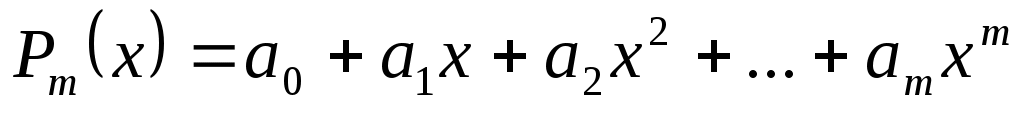 , записанных в следующем порядке: , записанных в следующем порядке: 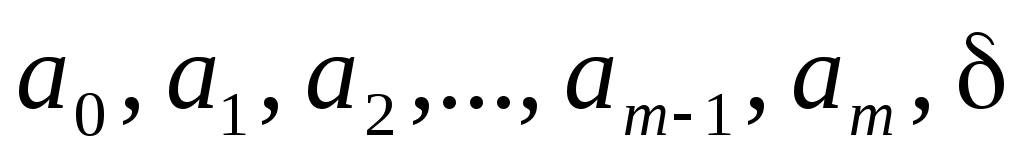 . Последняя . Последняя 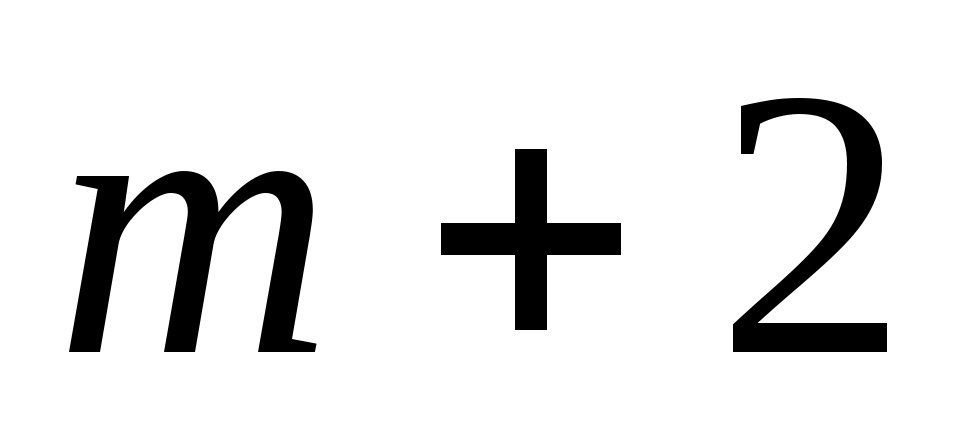 компонента вектора результата содержит среднюю квадратическую ошибку представления исходных табличных данных построенным сглаживающим многочленом: компонента вектора результата содержит среднюю квадратическую ошибку представления исходных табличных данных построенным сглаживающим многочленом:

Для нашего примера
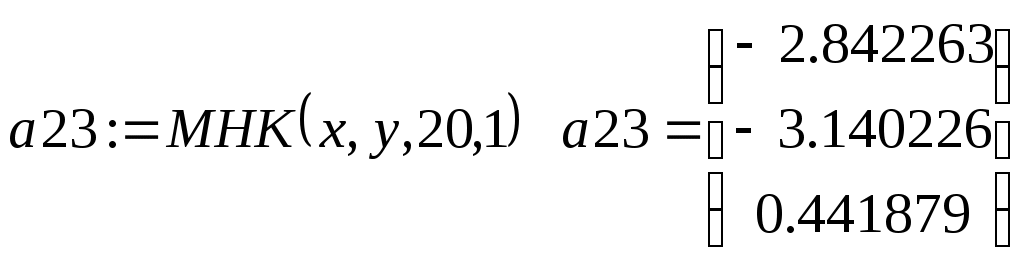 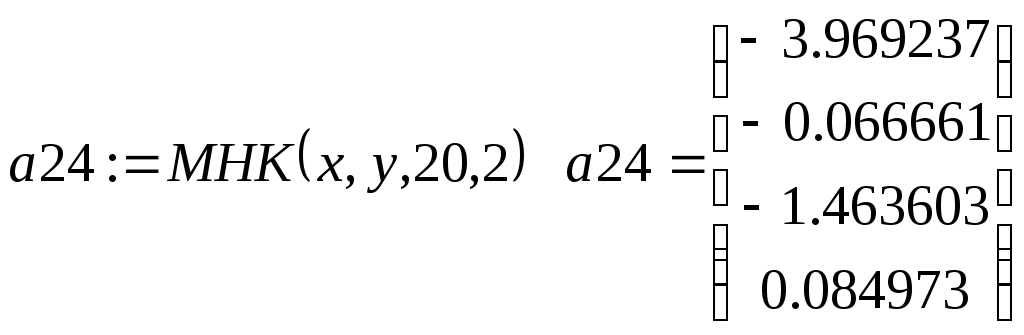
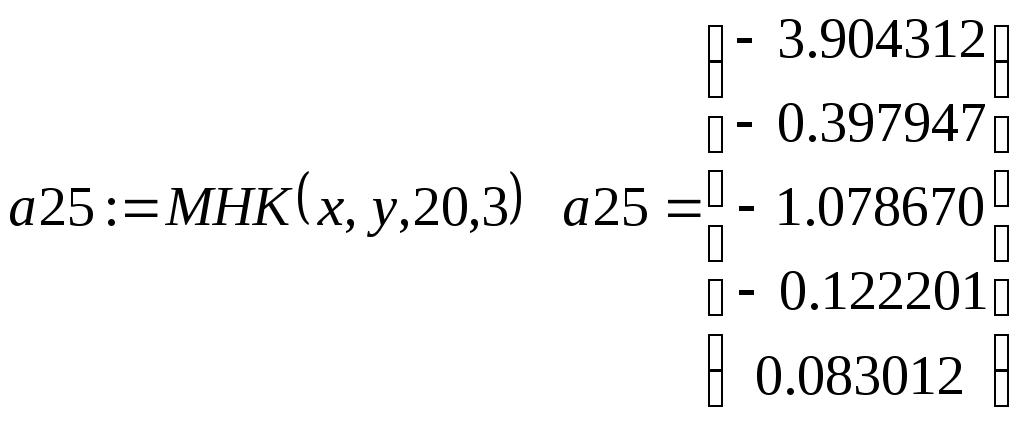 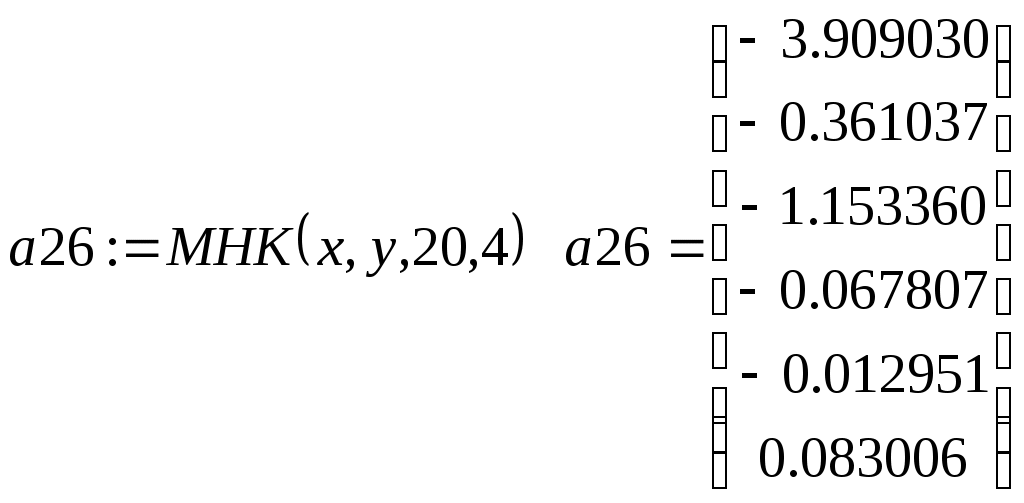
Видно, что для исходной таблично заданной функции многочленом наилучшего приближения является уже полученный ранее многочлен второй степени 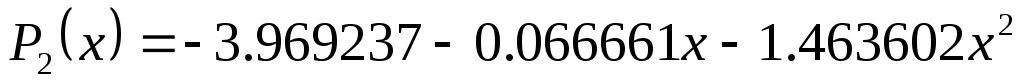 . Дальнейшее усложнение модели (повышение степени многочлена) практически не изменяет среднюю квадратическую ошибку и, следовательно, не является оправданным. . Дальнейшее усложнение модели (повышение степени многочлена) практически не изменяет среднюю квадратическую ошибку и, следовательно, не является оправданным.
Задание № 1. По методу наименьших квадратов аппроксимировать таблично заданную функцию 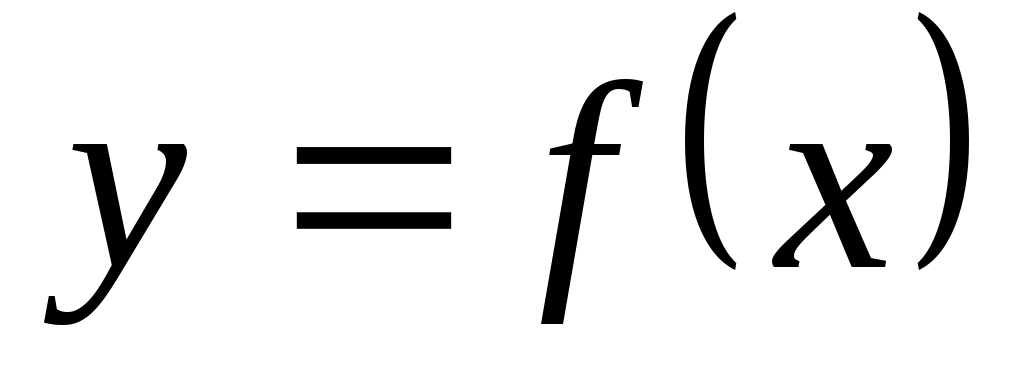 многочленом наилучшего среднеквадратического приближения многочленом наилучшего среднеквадратического приближения 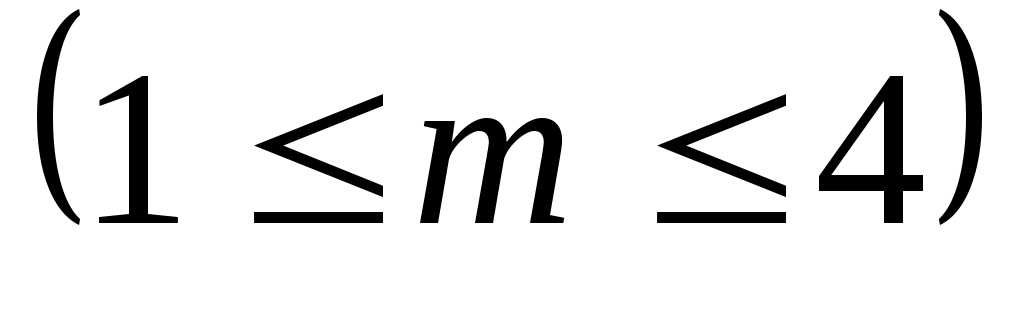 . .
Т а б л и ц а 1
-
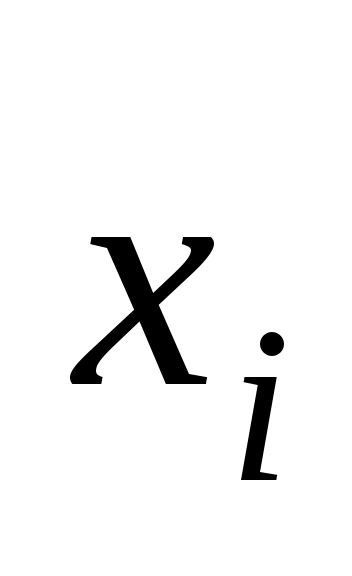
|
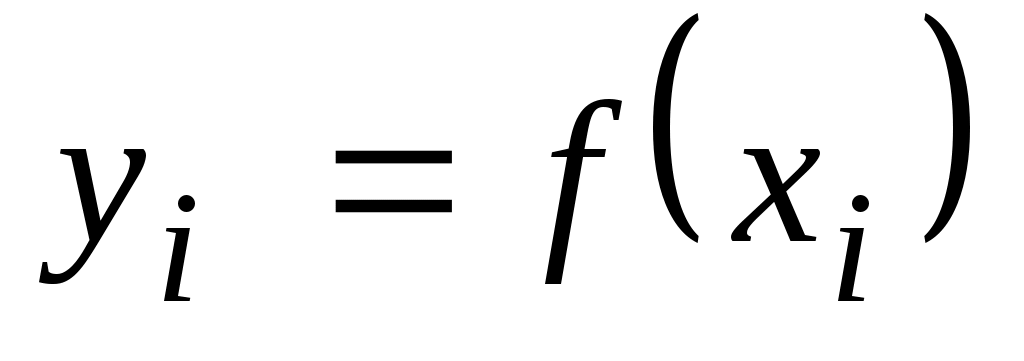
| |
Номера вариантов
| |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
0.1
|
3.15
|
20.95
|
2.20
|
6.00
|
3.13
|
0.07
|
12.28
|
-9.10
|
9.84
|
3.09
| |
0.2
|
3.04
|
20.51
|
2.18
|
7.04
|
3.19
|
0.17
|
12.53
|
-9.21
|
10.01
|
3.31
| |
0.3
|
3.02
|
21.96
|
1.87
|
7.21
|
3.17
|
0.21
|
12.50
|
-8.99
|
11.10
|
3.72
| |
0.4
|
2.97
|
21.83
|
1.85
|
7.40
|
3.52
|
0.31
|
12.53
|
-8.95
|
12.16
|
3.77
| |
0.5
|
2.87
|
21.79
|
1.77
|
7.20
|
3.62
|
1.10
|
12.75
|
-9.13
|
13.05
|
3.78
| |
0.6
|
2.98
|
22.72
|
1.62
|
7.70
|
3.72
|
1.09
|
12.85
|
-9.23
|
14.35
|
3.97
| |
0.7
|
2.81
|
25.80
|
1.57
|
7.36
|
4.03
|
1.12
|
12.77
|
-9.21
|
15.19
|
4.00
| |
0.8
|
2.70
|
27.33
|
1.27
|
7.61
|
4.39
|
-0.37
|
12.76
|
-9.43
|
15.50
|
4.51
| |
0.9
|
2.66
|
28.21
|
1.05
|
7.56
|
4.72
|
-0.22
|
12.73
|
-9.57
|
15.74
|
4.43
| |
1.0
|
2.50
|
30.45
|
0.68
|
7.50
|
4.85
|
-0.48
|
12.85
|
-9.44
|
16.03
|
4.58
| |
1.1
|
2.60
|
30.37
|
0.55
|
7.51
|
5.12
|
-0.84
|
12.51
|
-9.44
|
16.56
|
4.58
| |
1.2
|
2.36
|
34.51
|
-0.10
|
7.53
|
5.38
|
-0.93
|
12.34
|
-9.83
|
17.49
|
4.54
| |
1.3
|
2.09
|
36.29
|
-0.41
|
7.45
|
5.96
|
-1.15
|
12.22
|
-9.78
|
17.79
|
4.82
| |
1.4
|
2.07
|
38.53
|
-1.00
|
7.27
|
6.40
|
-1.44
|
11.84
|
-9.81
|
18.03
|
4.90
| |
1.5
|
2.01
|
41.90
|
-1.19
|
7.20
|
6.58
|
-1.90
|
11.67
|
-10.06
|
18.82
|
4.77
| |
1.6
|
1.81
|
44.52
|
-1.56
|
7.25
|
7.09
|
-2.25
|
11.27
|
-10.41
|
19.50
|
4.81
| |
1.7
|
1.53
|
48.91
|
-2.08
|
7.35
|
7.32
|
-2.65
|
11.06
|
-10.40
|
20.28
|
5.00
| |
1.8
|
1.64
|
50.68
|
-2.61
|
6.97
|
7.94
|
-3.06
|
10.73
|
-10.70
|
21.21
|
4.97
| |
1.9
|
1.29
|
56.36
|
-3.37
|
7.20
|
8.47
|
-3.66
|
10.35
|
-10.96
|
22.63
|
5.08
| |
2.0
|
1.11
|
59.14
|
-3.86
|
7.06
|
9.00
|
-4.01
|
10.09
|
-11.91
|
22.90
|
5.08
|
Т а б л и ц а 2
-
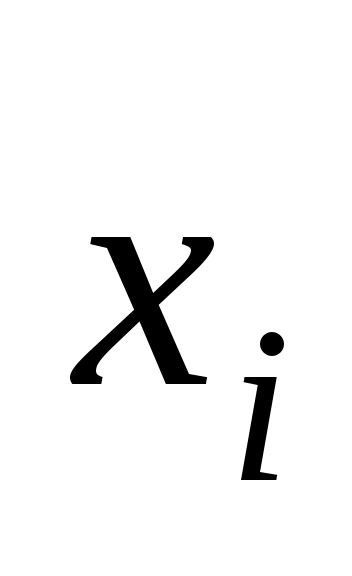
|
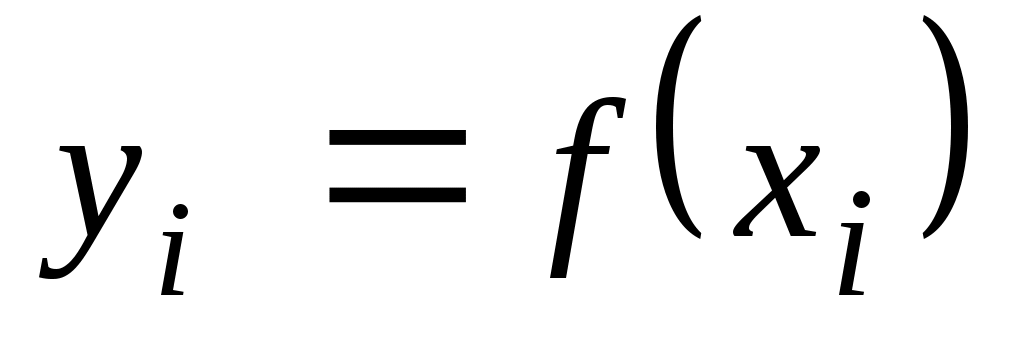
| |
Номера вариантов
| |
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
0.1
|
8.15
|
-6.90
|
0.17
|
3.30
|
1.04
|
0.08
|
3.09
|
-0.86
|
0.00
|
-0.65
| |
0.3
|
8.41
|
-7.01
|
0.07
|
2.49
|
1.47
|
0.14
|
3.25
|
-0.77
|
-0.09
|
-1.00
| |
0.5
|
8.58
|
-7.19
|
0.17
|
3.02
|
1.78
|
0.37
|
3.48
|
-0.56
|
-0.26
|
-0.87
| |
0.7
|
8.84
|
-7.11
|
0.05
|
3.27
|
2.01
|
0.36
|
3.47
|
-0.46
|
-0.20
|
-0.89
| |
0.9
|
9.28
|
-7.31
|
0.12
|
3.43
|
2.19
|
0.44
|
3.55
|
-0.28
|
-0.29
|
-0.75
| |
1.1
|
9.46
|
7.78
|
0.00
|
3.70
|
2.60
|
0.48
|
3.59
|
-0.24
|
-0.14
|
-0.59
| |
1.3
|
10.02
|
-7.64
|
0.01
|
3.70
|
2.93
|
0.27
|
3.28
|
-0.36
|
-0.26
|
-0.44
| |
1.5
|
10.11
|
-7.85
|
-0.05
|
3.85
|
3.22
|
0.39
|
3.50
|
-0.43
|
-0.45
|
-0.61
| |
1.7
|
10.61
|
-8.18
|
-0.21
|
3.89
|
3.50
|
0.50
|
3.61
|
-0.56
|
-0.43
|
-0.17
| |
1.9
|
11.03
|
-8.39
|
-0.50
|
3.98
|
4.01
|
0.48
|
3.59
|
-0.59
|
-0.71
|
0.13
| |
2.1
|
11.34
|
-8.79
|
-0.50
|
4.02
|
4.22
|
0.69
|
3.80
|
-0.70
|
-0.70
|
0.53
| |
2.3
|
11.86
|
-9.02
|
-0.86
|
4.21
|
4.71
|
0.50
|
3.61
|
-1.01
|
-1.00
|
0.67
| |
2.5
|
12.33
|
-9.48
|
-1.24
|
4.22
|
5.23
|
0.31
|
3.42
|
-1.03
|
-1.01
|
1.00
| |
2.7
|
12.81
|
-9.93
|
-1.47
|
4.37
|
5.78
|
0.37
|
3.48
|
-1.47
|
-1.17
|
1.34
| |
2.9
|
13.21
|
-10.26
|
-1.79
|
4.36
|
6.27
|
0.43
|
3.54
|
-1.68
|
-1.39
|
1.49
| |
3.1
|
13.67
|
-10.91
|
-2.25
|
4.39
|
6.75
|
0.33
|
3.44
|
-1.93
|
-1.22
|
1.81
| |
3.3
|
14.23
|
-11.41
|
-2.55
|
4.54
|
7.16
|
0.31
|
3.42
|
-2.28
|
-1.43
|
2.37
| |
3.5
|
14.68
|
-11.91
|
-3.18
|
4.33
|
7.76
|
0.09
|
3.20
|
-2.53
|
-1.81
|
2.72
| |
3.7
|
15.35
|
-12.30
|
-3.60
|
4.54
|
8.30
|
0.08
|
3.19
|
-2.93
|
-1.84
|
3.03
| |
3.9
|
15.93
|
-13.00
|
-3.93
|
4.53
|
9.00
|
0.03
|
3.14
|
-3.07
|
-1.99
|
3.51
|
Т а б л и ц а 3
-
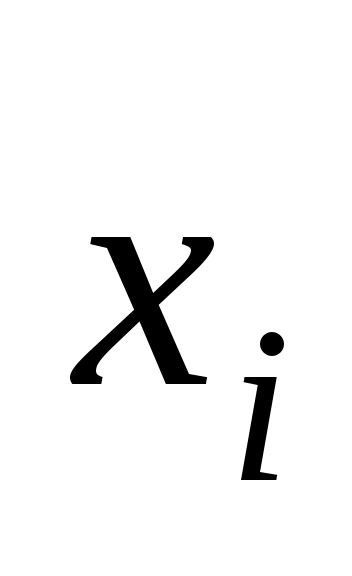
|
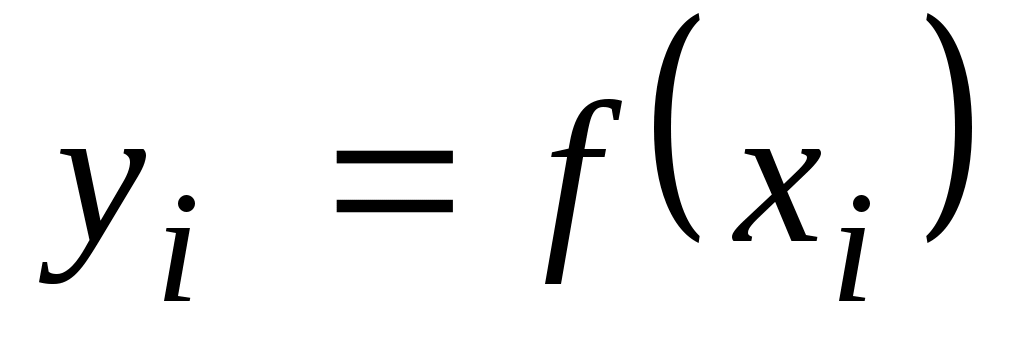
| |
Номера вариантов
| |
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
0.15
|
0.16
|
1.89
|
-1.92
|
1.10
|
-2.80
|
0.00
|
4.01
|
0.12
|
4.13
|
2.97
| |
0.30
|
0.02
|
2.07
|
-1.60
|
1.20
|
-2.66
|
0.01
|
4.06
|
0.31
|
4.11
|
3.07
| |
0.45
|
0.28
|
2.30
|
-1.57
|
1.18
|
-2.36
|
0.24
|
3.88
|
0.48
|
3.87
|
3.04
| |
0.60
|
0.42
|
2.26
|
-1.41
|
1.14
|
-2.41
|
0.74
|
3.98
|
0.45
|
3.74
|
3.30
| |
0.75
|
0.31
|
2.34
|
-1.36
|
1.17
|
-2.13
|
1.02
|
4.36
|
0.84
|
3.85
|
3.27
| |
0.90
|
0.41
|
2.66
|
-0.97
|
1.00
|
-1.82
|
1.31
|
4.18
|
0.73
|
3.71
|
3.54
| |
1.05
|
0.42
|
2.88
|
-0.59
|
0.99
|
-1.74
|
1.53
|
4.16
|
0.77
|
3.53
|
3.79
| |
1.20
|
0.36
|
2.85
|
-0.71
|
0.95
|
-1.76
|
1.90
|
4.51
|
0.64
|
3.56
|
4.07
| |
1.35
|
0.45
|
3.16
|
-0.15
|
0.54
|
-1.64
|
2.29
|
4.53
|
0.74
|
3.19
|
4.30
| |
1.50
|
0.65
|
3.49
|
0.01
|
0.32
|
-1.46
|
2.61
|
4.38
|
0.53
|
3.04
|
4.51
| |
1.65
|
0.67
|
3.88
|
0.22
|
0.15
|
-1.30
|
3.15
|
4.76
|
0.28
|
2.83
|
4.83
| |
1.80
|
0.53
|
4.22
|
0.63
|
0.02
|
-1.27
|
3.42
|
4.66
|
0.24
|
2.54
|
5.06
| |
1.95
|
0.50
|
4.45
|
1.07
|
-0.30
|
-1.22
|
3.89
|
4.82
|
0.00
|
2.41
|
5.40
| |
2.10
|
0.35
|
4.99
|
1.42
|
-0.40
|
-1.11
|
4.58
|
4.77
|
0.03
|
1.97
|
5.83
| |
2.25
|
0.35
|
5.36
|
1.68
|
-0.90
|
-1.02
|
4.82
|
5.12
|
0.35
|
1.78
|
6.54
| |
2.40
|
0.13
|
5.71
|
2.49
|
-1.37
|
0.89
|
5.42
|
5.23
|
0.46
|
1.53
|
6.68
| |
2.55
|
0.39
|
6.51
|
2.57
|
-1.65
|
0.89
|
6.07
|
5.40
|
0.88
|
1.04
|
7.36
| |
2.70
|
0.14
|
7.35
|
3.09
|
-2.00
|
-1.02
|
6.44
|
5.84
|
1.27
|
0.86
|
7.91
| |
2.85
|
0.14
|
8.02
|
3.40
|
-2.42
|
0.97
|
7.15
|
5.86
|
1.68
|
0.48
|
8.39
| |
3.00
|
0.09
|
8.96
|
4.00
|
-3.13
|
0.99
|
7.66
|
6.01
|
1.98
|
-0.09
|
8.98
|
|
|
|
 Скачать 2.21 Mb.
Скачать 2.21 Mb.