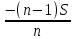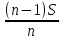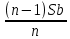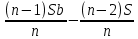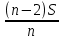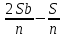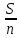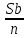Экономические задачи. эк зад. 50 экономических задач

• Название: 50 экономических задач
• Анкор: Экономические задачи
• Дата: 20.03.2022
• Размер: 206.56 Kb.
• Имя файла: эк зад.docx
• Тип: Документы; #405720
• страница: 1 из 8

ПРОЕКТ ПО МАТЕМАТИКЕ

«50 ЭКОНОМИЧЕСКИХ ЗАДАЧ»

Выполнила: Позднякова Полина,

ученица 11 «А» класса

МБОУ Щёлковский лицей №7.

Руководитель: Позднякова Ольга Вячеславовна.

2018 год

Оглавление

1. 
   Введение 3
   
2. 
   Теория
   
   1. 
      Проценты 5
      
   2. 
      Платежи 5
      
   3. 
      Таблицы 5
      
   4. 
      Арифметическая и геометрическая прогрессии 7
      
   5. 
      Производная 8
      
3. 
   Практическое решение экономических задач
   

3.1 Кредиты

1 тип: Нахождение количества лет (месяцев) выплаты кредита. (Аннуитетные платежи) 10

2 тип: Вычисление процентной ставки по кредиту. (Фиксированные платежи) 13

3 тип: Нахождение суммы кредита. (Аннуитетные платежи) 16

4 тип: Нахождение ежегодного ( ежемесячного) транша.(Аннуитетные платежи) 19

5 тип: Нахождение разницы. (Аннуитетные платежи) 22

6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи) 25

7 тип: Задачи, связанные с дифференцированными платежами 28

8 тип: Нестандартные задачи, связанные с кредитом 32

3.2 Вклады 36

3.3 Задачи на оптимизацию 44

4. 
   Нестандартные задачи 56
   

4.Заключение 61

5.Список литературы 61

1. 
   Введение
   

Экономическую задачу ввели в экзамен ЕГЭ «Профиль по математике» только с 2015 года. Она стала называться заданием номер 17 и по своей сложности находится на одном уровне с заданиями на параметры и теорию чисел.

Приведу примеры статистики сдачи ЕГЭ по математике (профильный уровень) за 2016 и 2017 годы (использовала данные с сайта ФИПИ)

Год	Не сдали экзамен	Сдали экзамен	Средний балл	Количество 100-бальников
2017	14,34%	85,66%	47,1 балл	224 учащихся
2016	15,33%	84,67%	46,3 балла	296 учащихся

Решение задания номер 17

Год	Набрали ненулевой балл (от сдавших экзамен учащихся)	Набрали ненулевой балл (от всех учащихся)	Набрали максимальный балл (от сдавших экзамен учащихся)	Набрали максимальный балл (от всех учащихся)	Доля учащихся
2017	14,8%	12,68%	8%	6,85%	Каждый 15
2016	13%	11%	Нет данных	Нет данных	Нет данных

Такая статистика решения экономической задачи объясняется и сложностью задания и просто тем, что такой темы просто нет в наших учебниках по алгебре. Поэтому у меня и появилась идея написать методичку «50 экономических задач для подготовки к сдаче ЕГЭ «Профиль по математике»», целью которой является подготовка учащихся к ЕГЭ.

Конечно, на различных сайтах и в математической литературе можно найти решения таких задач, но зачастую либо они содержат много лишней информации, либо они решены непонятным для меня способом. Я же использовала табличный метод, так как считаю его самым наглядным и простым.

Из необходимых знаний и умений мне понадобились:

1. 
   Определение понятия «Процент»
   
2. 
   Определение понятий «Фиксированные платежи», «Аннуитетные платежи» и «Дифференцируемые платежи».
   
3. 
   Виды мною созданных таблиц
   
4. 
   Определение, формулы n-ого члена и суммы n первых членов арифметической и геометрической прогрессий
   
5. 
   Знание алгоритмов нахождения промежутков возрастания (убывания) функций и точек экстремума.
   

Каждую неделю, начиная с сентября 2016 года, я решала по две экономических задачи. Условия таких задач я брала:

1. 
   ЕГЭ 2018 под редакцией А. Л. Семенова, И.В. Ященко
   
2. 
   Открытый банк заданий ЕГЭ fipi.ru
   
3. 
   Сайт «Решу ЕГЭ»
   
4. 
   И мой любимый сайт «Алекс Ларин»
   

Всего я решила примерно 152 задачи, выбрала из них 50 задач, разделив их условно на типы:

Кредиты.

1 тип: Нахождение количества лет (месяцев) выплаты кредита. (Аннуитетные платежи) - 3 задачи

2 тип: Вычисление процентной ставки по кредиту. (Фиксированные платежи) – 3 задачи

3 тип: Нахождение суммы кредита. (Аннуитетные платежи)- 3 задачи

4 тип: Нахождение ежегодного (ежемесячного) транша. (Аннуитетные платежи)- 3 задачи

5 тип: Нахождение разницы. (Аннуитетные платежи) – 3 задачи

6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)- 3 задачи

7 тип: Задачи, связанные с дифференцированными платежами.- 3 задачи

8 тип: Нестандартные задачи, связанные с кредитом.- 4 задачи

Вклады. – 8 задач

Задачи на оптимизацию. -12 задач

Нестандартные задачи.-5 задач

Конечно, наиболее трудными среди экономических задач считаются задачи на тему «Оптимизация» и нестандартные задачи с сайта «Алекс Ларин».

2.Теория.

Решение финансовых задач основывается на использовании различных математических моделей: уравнений, неравенств, их систем с привлечением процентов, арифметической и геометрической прогрессий и производной. Приведу основные определения, понятия, таблицы и формулы.

2.1 Проценты.

Определение: один процент – это одна сотая доля. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.

Пример: 5% от 80 это будет 0,05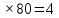

r% от 14 это будет 0,01r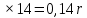

При решении задач необходимо понимать механизм начисления процентов по вкладам или кредитам. Например, если банк выдаёт кредит (S) клиенту, то через год клиент должен банку не только сумму кредита, но и некий процент (r). Возникает необходимость введения нового коэффициента b, b=1+0,01r. С учётом этого , долг клиента банку через год можно записать следующим образом:

S + r% от S = S + 0,01r 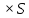= S (1 + 0,01r) = bS

2.2 Платежи.

В задачах по теме «Кредит» используют о три основных вида платежа:

1. 
   Фиксированные платежи (платежи, которые чётко оговариваются в условии задачи)
   
2. 
   Аннуитетные платежи (постоянные ежемесячные или ежегодные платежи, которые не меняются на протяжении всего периода кредитования)
   
3. 
   Дифференцируемые платежи (ежемесячные или ежегодные платежи, уменьшающиеся к концу срока кредитования и обеспечивающие уменьшение суммы долга на одну и ту же величину)
   

2.3 Таблицы.

При решении задач, связанных с аннуитетными платежами мне было очень удобно заполнять следующую таблицу:

S – сумма кредита

r% - годовые (ежемесячные) проценты

b=1+0,01r – коэффициент

х – ежегодная (ежемесячная) выплата

Год	Долг с %	Выплата	Долг после выплаты
0			S
1 год	Sb	x	Sb-x
2 год	(Sb-x)b=Sb2-xb	x	Sb2-xb-x
3 год	(Sb2-xb-x)b=Sb3-x b2-xb	x	Sb3-x b2-xb-x
4 год	(Sb3-x b2-xb-x)b= Sb4-xb3-xb2-xb	x	Sb4-xb3-xb2-xb-x
5 год	(Sb4-xb3-xb2-xb-x)b= Sb5-xb4-xb3-xb2-xb	x	Sb5-xb4-xb3-xb2-xb-x
6 год	(Sb5-xb4-xb3-xb2-xb-x)b= Sb6-xb5-xb4-xb-3xb2-xb	x	Sb6-xb5-xb4-xb-3xb2-xb-x
n год	Sbn-xbn-1-xbn-2-…-xb2-xb	x	Полная выплата, долг равен 0

При решении задач, связанных с дифференцированными платежами я использовала следующую таблицу:

Месяц	Долг с %	Выплата	Долг после выплаты
0			S
1	Sb	Sb
2
n-1
n			0

При решении задач по теме «Вклады»:

Год	Вклад с %
0
1	Sb
2	Sb2
n	Sbn

При решении задач, в которых осуществлялись какие-либо действия (пополнение или снятие денег с вклада):

х – действие

Год	Вклад с %	Действие	Вклад после действия.
0			S
1 год	Sb	+х	Sb+x
2 год	b(Sb+x)= Sb2+xb	+х	Sb2+xb+x
3 год	b(Sb2+xb+x)=Sb3_+хb2+xb	Снял вклад

2.4 Арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Определение. Последовательность чисел, в которой каждое следующее отличается от предыдущего ровно на одну и ту же величину, называется арифметической прогрессией.

Любой член арифметической прогрессии вычисляется по формуле: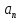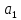

= + (n-1)d

Формула суммы n-первых членов арифметической прогрессии

S_n =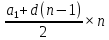

С учётом этой формулы : (n-1) + (n-2) +…+3+2+1 = =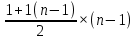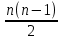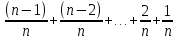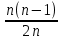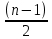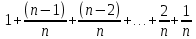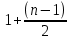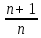

= =

= =

Геометрическая прогрессия

Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Любой член геометрической прогрессии вычисляется по формуле:

b_n =b₁· q^n-1

Формула суммы n-первых членов геометрической прогрессии

S_n=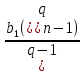

Из этой формулы следует: b^n-1+b^n-2 +…+b²+b+1=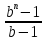

2.5 Производная.

Достаточные признаки возрастания и убывания функции:

Если производная данной функции положительна для всех значений х в интервале (а; в), т.е. f'(x) > 0, то функция в этом интервале возрастает.  
Если производная данной функции отрицательна для всех значений х в интервале (а; в), т.е. f'(x) < 0, то функция в этом интервале убывает

Порядок нахождения промежутков монотонности:

 Найти область определения функции.

1. Найти производную функции.

2. Найти критические точки (точки, в которых производная не существует) и стационарные (точки, в которых производная равна нулю). Исследовать знак производной в промежутках, на которые найденные точки делят область определения функции.

 Достаточное условие существования максимума состоит в смене знака производной при переходе через критическую точку с "+" на "-", а для минимума с "-" на "+". Если при переходе через критическую точку смены знака производной не происходит, то в данной точке экстремума нет

Пример:

f(x) =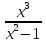

Найдём производную.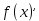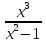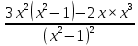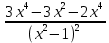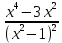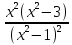

=( )^, = = = =
Критические точки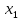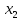 = 1, = -1

Стационарные точки 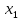= = 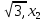- 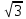, 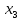= 0



Ответ: возрастает (- ;+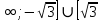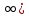

убывает ; -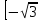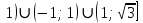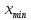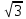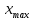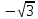

= ; = .