ГОСЫ. ГОСы. 76. каскадная модель жизненного цикла ис (основные этапы разработки по каскадной модели. Достоинства и недостатки каскадной модели)
 Скачать 5.37 Mb.
|
|
Рисунок 1. Различные множества подзадач для задачи А 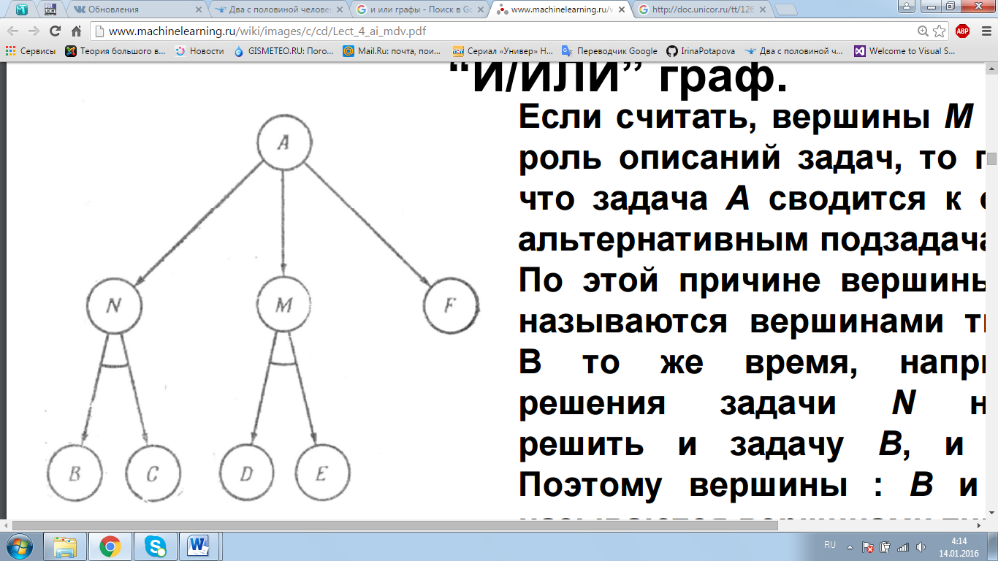 Рисунок 2 И-ИЛИ граф Если считать, вершины M и N играют роль описаний задач, то получается, что задача A сводится к одиночным альтернативным подзадачам N, M и F. По этой причине вершины N, M и F называются вершинами типа “ИЛИ”. В то же время, например, для решения задачи N необходимо решить и задачу B, и задачу C. Поэтому вершины: B и C, D и E называются вершинами типа “И”. Структура на рис.2 носит название “И/ИЛИ” графа. Такой граф характеризуется тем, что если вершина имеет непосредственно следующие за ней вершины, то либо все они являются “ИЛИ” вершинами, либо все они –“И”. Если вершины “И” отсутствуют, то получаем обычный граф перебора в пространстве состояний. На языке “И/ИЛИ” графов применение одиночного оператора fi∈F к некоторому описанию задачи будет означать, что по очереди сначала будет построена промежуточная “ИЛИ” вершина, а затем непосредственно следующие за ней “И” вершины. Разрешимость вершин в “И/ИЛИ” графе. Начальная вершина “И/ИЛИ” графа соответствует описанию исходной задачи. Те вершины, которые соответствуют описаниям элементарных задач, называются заключительными вершинами. Цель поиска на “И/ИЛИ” графе – показать, что начальная вершина разрешима. Определение разрешимости вершины в “И/ИЛИ” графе дается рекурсивно следующим образом •Заключительные вершины разрешимы как соответствующие элементарным задачам. •Если у вершины, не являющейся заключительной, непосредственно следующие за ней вершины оказались вершинами “ИЛИ”, то она разрешима только тогда, когда разрешима по крайней мере одна из этих вершин. •Если у вершины, не являющейся заключительной, непосредственно следующие за ней вершины оказались вершинами “И”, то она разрешима только тогда, когда разрешима каждая из этих вершин. Определение. Решающий граф определяется как подграф из разрешимых вершин, который показывает, что начальная вершина разрешима в соответствии с приведенным определением. Неразрешимые вершины в “И/ИЛИ” графе. Определение неразрешимой вершины – дается рекурсивно: •Вершины, не являющиеся заключительными и не имеющие следующих за ними вершин, неразрешимы. •Если у вершины, не являющейся заключительной, непосредственно следующие за ней вершины оказались вершинами “ИЛИ”, то она неразрешима тогда и только тогда, когда неразрешима каждая из этих вершин. •Если у вершины, не являющейся заключительной, непосредственно следующие за ней вершины оказались вершинами “И”, то она неразрешима тогда и только тогда, когда неразрешима по крайней мере одна из этих “И” вершин. Аналогично решению задач в пространстве состояний, граф “И/ИЛИ”, как правило, определяется неявно посредством описания исходной задачи и операторов редукции задачи. Как и для поиска в пространстве состояний, удобно ввести оператор γ построения непосредственно следующих (дочерних) вершин, его применение означает применение всех применимых операторов fi∈F.  128. СИСТЕМНЫЙ ПОДХОД К ПРОЕКТИРОВАНИЮ ИИС. Системный подход — это методология специального научного познания и социальной практики, а также объяснительный принцип, в основе которого лежит исследование объектов как систем. 1)Выбор и изучение предметной области, изучение основных понятий, проблем, задач. 2)Формулирование цели 3) Определение связей с внешней средой и выявление внешних факторов подлежащих учету (определяется какая система статическая или динамическая возможности интеграции с другими БД для получения данных). 4) Выявление всех неопределенностей (та информация, на основании которой …) 5) Проектирование БЗ (выбор модели представления знаний, обоснование полученных данных) 6) Выбор формальной модели машины вывода(решатель) формирование заключительного вывода (как будет организован вывод). 7) Выбор диалоговой системы- предполагает общение с разработчиками и потребителем. Необходимо при диагностике системы создателем и должна объяснять потребителю полученное решение на доступном языке (указания на ошибки пользователя). 8) Построение концептуальной модели ИС на уровне структурной схемы и функциональной системы. 9) Разработка ПО … диагностика работы, тестирование => прототип системы. 10) Тестирование прототипа в реальных условиях. 129. ПРИНЯТИЕ КОЛЛЕКИВНЫХ РЕШЕНИЙ. ОРГАНИЗАЦИОННЫЕ СТРУКТУРЫ (КОМИТЕТ, ИЕРАРЗИЯ, ПОЛИАРХИЯ). МНОЖЕСТВО АЛЬТЕРНАТИВ. ПРЕДПОЧТЕНИЕ ЭКСПЕРТА. КОЛЛЕКТИВНОЕ ПРЕДПОЧТЕНИЕ. Групповое принятие решений - это ситуация, с которой люди коллективно делают выбор из имеющихся альтернатив. Таким образом, решение больше не может быть приписано какому-либо отдельному человеку, который является членом группы. КЛПР – Коллективное лицо принимающее решение ОЛПР – ответственное лицо, принимающее решение ГЛПР – группа лиц, принимающих решение Сложности принятия коллективного решения - неоднозначность выбора при наличии нескольких показателей качества полученного решения. Гипотезы принятия коллективного решения: • КЛПР представляет собой 2х уровневую структуру ( 1 – рабочая группа - Группа Лиц Принимающих Решение, 2 – ответственное лицо , - Лицо Принимающее Решение) • ГЛПР совокупность лиц(экспертов) представляющие все заинтересованные стороны в разрешении данной ситуации. • Частные показатели качества могут иметь разную важность для принятия решения. Для организации Коллективного принятия решения формируется одна из важных структур – Комитеты • В комитете рассматриваемый проект дается на ознакомление всем экспертам, далее проводится голосование (каждый эксперт дает свое предпочтение всем альтернативам) решение, у которого наибольшее число голосов, становится коллективным. • При иерархии эксперты выстроены в последовательность (знакомятся с проектом последовательно) ! любое решение отклоняется, если его отклонил хотя бы 1 эксперт, или направляется дальше, если предыдущий его одобрил. ! данный вид организации возможен при высокой квалификации экспертов. • При полиархии каждое решение отправляется одному из экспертов случайным образом. Решение принимается при его положительном заключении. Множество альтернатив – множество допустимых вариантов решения с набором числовых значений качества данного решения. Предпочтение эксперта – субъективное мнение эксперта относительно множества альтернатив. Коллективное предпочтение – групповое предпочтение на множестве альтернатив. Считается, что наилучшее решение соответствует наилучшему набору числовых показателей решения. 130. ПОСТАНОВКА ЗАДАЧИ ПРИНЯТИЯ КОЛЛЕКТИВНОГО РЕШЕНИЯ. ГОЛОСОВАНИЕ И ВЫБОР. МОЕЛИ КОНДОРСЕ И БОРДА. ПАРАДОКС КОНДОРСЕ. ПРИМЕРЫ Постановка задачи принятия коллективного решения. Голосование и выбор X- конечное множество альтернатив xj принадлежитX, j = 1..n Альтернатива – допустимый вариант решения с набором числовых значений качества данного решения. J_k^i , k =1..r, где r число показателей качества Наилучшему решению соответствует наилучшему набору J_k^i Считается что Группа Лиц Принимающих решение состоит из m экспертов, при этом известны предпочтения iго эксперта на множестве альтернатив X(>_ ^i, i = 1..m на X). Требуется найти коллективное решение, под которым понимается групповое предпочтение на множестве альтернатив X. Голосование используется, когда нет показателей качества и нет известных значений квалификации каждого из экспертов. Известны только предпочтения экспертов (Модель Кондорсе). Выбор применяется, если известны как предпочтения, так и показатели качества, а так же квалификации экспертов (Линейная модель) Модель Кондорсе Есть конечное множество альтернатив. Х, хj э Х, j э (1…n) Альтернатива – допустимый вариант решения с набором числовых значений количества.(J_k^i k=1….r число показателей) считается что Группа Лиц, принимающих решение. Состоит из m экспертов, при этом известны предпочтениям i-го эксперта на множ. альтернатив Х. Х>^i X,i=1…m Требуется найти коллективное решение. -Проводится ранжирование всех Хj и для каждой пары Xj и Xk считается число экспертов, которые предпочли j-ую k-ой. Наилучшей считается Xj для которой l(Xj, Xk) > l(Xk, Xj), ∀j,k=1…n j≠k Суть парадокса Кондорсе (парадокс голосования) состоит в выявлении предпочтений общества, где не существует единодушия по поводу принятия тех или иных альтернативных программ, т. е. в выборе оптимальной программы общественных предпочтений. Пример Множество альтернатив Х=(Х1….Х10) Число экспертов = 5 Предпочтения i-го эксперта, i=1…5 x2>x1>x3>x4>x5>x6>x7>x8>x9>x10 x2>x1>x3>x4…10 x1>x3>x4…10>x2 x3>x1>x4…10>x2 x4>x1>x3>x5…10>x2 Считаем число экспертов, которые предпочли Xj. Xk-ый l(x1>x2)=3 l(x1>x3)=4 l(x2>x1)=2 l(x3>x1)=1 x1 лучше х2 х1 лучше х3 х1>x3>x2>x4…10 Парадокс Кондоре Х=(х1, х2,х3) Эксперты=3 Считаем предпочтения экспертов l(x1>x2)=2 l(x2>x1)=1 => x1>x2 l(x2>x3)=2 l(x3>x2)=1 =>x2>x3 l(x1>x3)=1 l(x3>x1)=2 =>x3>x1 Предпочтения: 1. x1>x2>x3 2. x3>x1>x2 3. x2>x3>x1 Модель Борда - Согласно данной модели рез-ты голосования экспертов выражаются в виде числа баллов, набранных каждой альтернативой. Для этого вводится функция Борда в (Xj) В (X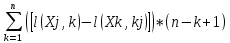j )=  , j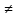 k, j=1*n, n- число альтернативИдея в том, что за 1 место дается n баллов, за последнее 1 балл. Пример: X=x1….x3 Эксперты=10
    Баллы за Места В (х1)=(4+2)*(3)+(2+1)*(2)+(0+1)*1=25 В (х2)=(2+0)*3+(4+1)*2+(2+1)*1=19 В (х3)=(1+1)*3+(2+0)*2+(4+2)*1=16 P.S. Не учитывает объективные оценки. Базируется на субъективной оценке экспертов 131. ЛИНЕЙНАЯ МОДЕЛЬ МНОГОКРИТЕРИАЛЬНОГО ВЫБОРА НАИЛУЧШЕЙ АЛЬТЕРНАТИВЫ. ПРИМЕР. Данная модель учитывает частные показатели качества каждой альтернативы, а также квалификацию эксперта в данной области. Обозначения: i = 1..m число экспертов; j =1..n число альтернатив xj; 1..r число частных показателей качества; Каждый эксперт может иметь свою оценку квалификации по данному критерию. 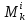 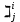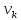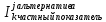– оценка квалификации iго эксперта по kму показателю качества (i = 1..m, k = 1..r); – предпочтение iго эксперта на множестве jх альтернатив( i =1..m, j =1..n);0  – важность kго критерия численное значение показателяБудем считать что наилучшее значение для каждого частного показателя достигается при его максимальном значении, выделим функцию предпочтительности jй альтернативы 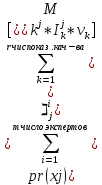 j = 1..n число альтернатив, Если считать что квалификация эксперта не связана с экономическим смыслом частного показателя, то выбор не будет зависеть от квалификации и M = 1. В качестве лучшей альтернативы Xj для которой pr(xj)>pr(xt) для любой t=1..n ! 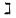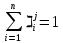каждый из  ,М,v э [0;1]; должно выполнятся условие  для всех j=1..mЕсли нужно найти минимальный показатель то нужно пересчитать 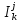 = ( 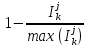)Пример Необходимо обосновать выбор наилучшего варианта производства (ООП)при заданном главном плане производства (ГППП) ГППП – количество продукта в определенное время ОПП – оперативно производственное планирование Заданы 3 показателя качества: I1 – комфортность производства операции одного типа запускались максимальными порциями I2 – равномерность производства , загрузка рабочих центров I3- минимальность срока изготовления, цикл производства каждой позиции должен быть минимальный
Число экспертов = 10, 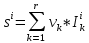 , тогда получим таблицу
Наилучшим является х1. Минусы В реальной жизни возникает множество Pr которые лежат в окрестности какого то значения Чувствителен к 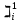 Линейность, использует теорию нечетких множеств В реальной жизни применяют модели коллективных решений, реализованных в информационных системах, которые получены с помощью ситуационного центра. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
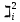*S(s=1.15)
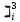*S(s=1.23)