|
МАТАН (шпоры). 8. Линейная зависимость и линейная независимость векторов. Векторы назыв коллинеарными,если лежат на
№19. Общее уравнение плоскости. П усть Q проходит через точку М0(х0,у0,z0) перпендикулярно вектору n=(А,В,С). Этими условиями определяется единственная плоскость в пространстве Охуz. Вектор , n назыв нормальным вектором плоскости Q. Возьмем в плоскости Q произвольную точку М(х,у,z). Тогда вектор М0М==(х-х0. у-у0, z- z0) будет перпендикулярен вектору n=(А,В,С). Следовательно, скалярное произведение этих векторов равно 0, т.е (n, М0М)=0. Полученное уравнение представим в координатной форме: А(х-х0) + В(у-у0) + С(z- z0)=0 – данное уравнение представляет уравнение плоскости, перпендикулярной данному вектору n=(А,В,С) и проходящей через данную точку М0(х0,у0, z0). Уравнение плоскости, записанное в виде Ах+Ву+Сz+D=0 (где D= -А х0 -В у0-С z0) назыв-ся усть Q проходит через точку М0(х0,у0,z0) перпендикулярно вектору n=(А,В,С). Этими условиями определяется единственная плоскость в пространстве Охуz. Вектор , n назыв нормальным вектором плоскости Q. Возьмем в плоскости Q произвольную точку М(х,у,z). Тогда вектор М0М==(х-х0. у-у0, z- z0) будет перпендикулярен вектору n=(А,В,С). Следовательно, скалярное произведение этих векторов равно 0, т.е (n, М0М)=0. Полученное уравнение представим в координатной форме: А(х-х0) + В(у-у0) + С(z- z0)=0 – данное уравнение представляет уравнение плоскости, перпендикулярной данному вектору n=(А,В,С) и проходящей через данную точку М0(х0,у0, z0). Уравнение плоскости, записанное в виде Ах+Ву+Сz+D=0 (где D= -А х0 -В у0-С z0) назыв-ся
|
общим уравнением плоскости. Условия парал-ти и перпен-ти плоскостей определяются условиями коллинеарности и перпендикулярности нормальных векторов n1=(А1,В1,С1) и n2=(А2,В2,С2). Условием пар-ости двух плоскостей явл пропорциональность коэффициентов при одноименных переменных А1/А2=И1/В2=С1/С2, а условием их перпендикулярности
А1А2+В1В2+С1С2=0. Если уравнение плоскости Ах+Ву+Сz+D=0 ни один из коэффициентов А, В, С, D не равен нулю, то это уравнение может быть преобразовано к виду х/а+у/в+z/с=1, где а=- D/А, в+- D/В, с=- D/С суть величины отрезков, которые плоскость отсекает на координатных осях. Уравнение данное назыв уравнением плоскости в отрезках. Нормальным уравнением плоскости назыв-ся ее уравнение, написанное в виде хcosα+уcosβ+z cosγ-р=0,
|
№19. Нормальным уравнением плоскости. где cosα, cosβ, cosγ-направляющие косинусы нормали плоскости, р- расстояние от начала координат до плоскости. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости. Расстояние от точки до плоскости. Пусть М*-какая угодно точка пространства, d – расстояние от нее до данной плоскости. Отклонение δ точки М* от данной плоскости назыв число + d, если точка М* и начало координат лежат по разные стороны от данной плоскости, и число – d, если они лежат по одну сторону от данной плоскости. Если точка М* имеет координаты х*,у*, z*, а плоскость задана нормальным уравнением хcosα+уcosβ+z cosγ-р=0, то отклонение точки М* от этой плоскости дается формулой δ=х* cosα+у*cosβ+z *cosγ-р. Очевидно, d= ׀δ׀. Уравнение плоскости Ах+Ву+Сz+D=0 приводится к
| нормальному виду умножением на нормирующий множитель, определяемый формулой μ=+- 1/√А2+В2+С2 знак нормирующего множителя берется противоположным знаку свободного члена нормируемого уравнения. Уравнение плоскости проходящей через три точки. Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат.
Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы 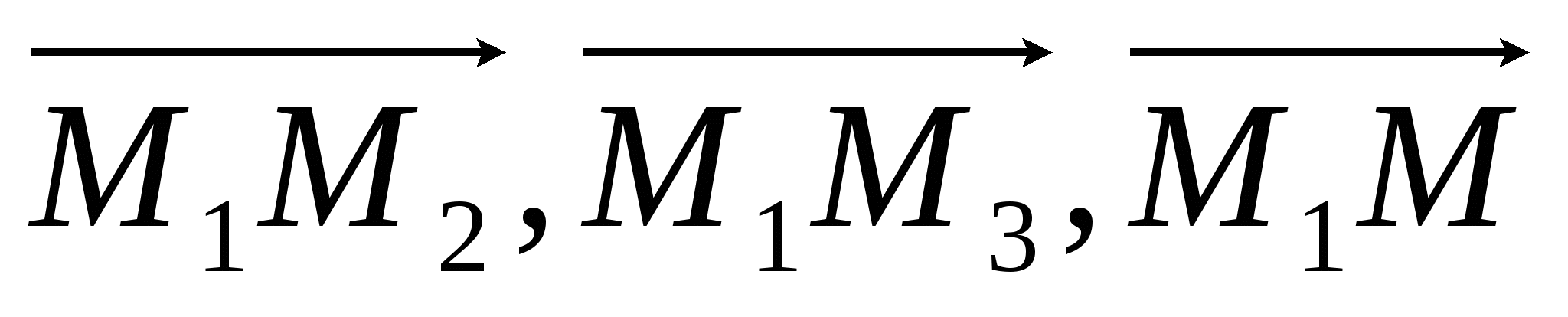 были компланарны. были компланарны. 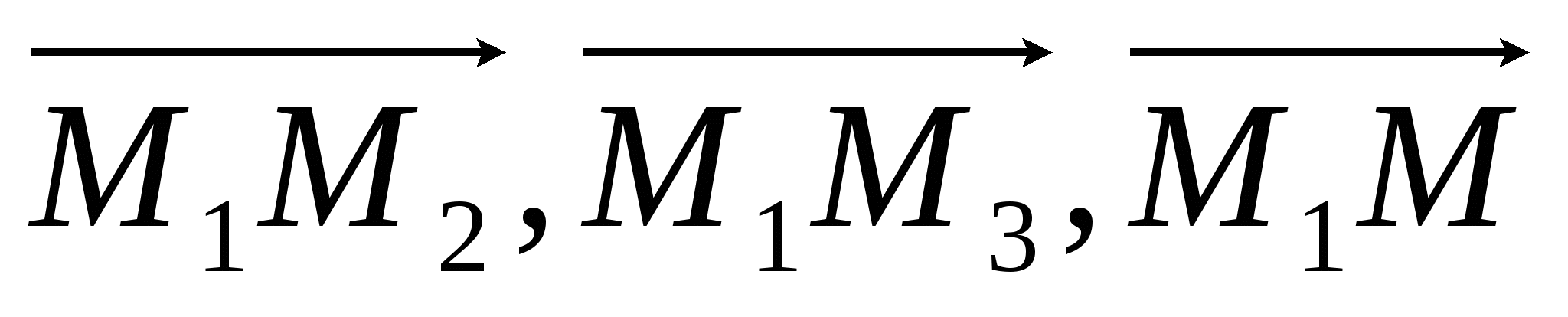 ) = 0 ) = 0
|
№19.Уравнение плоскости проходящей через три точки. Таким образом, 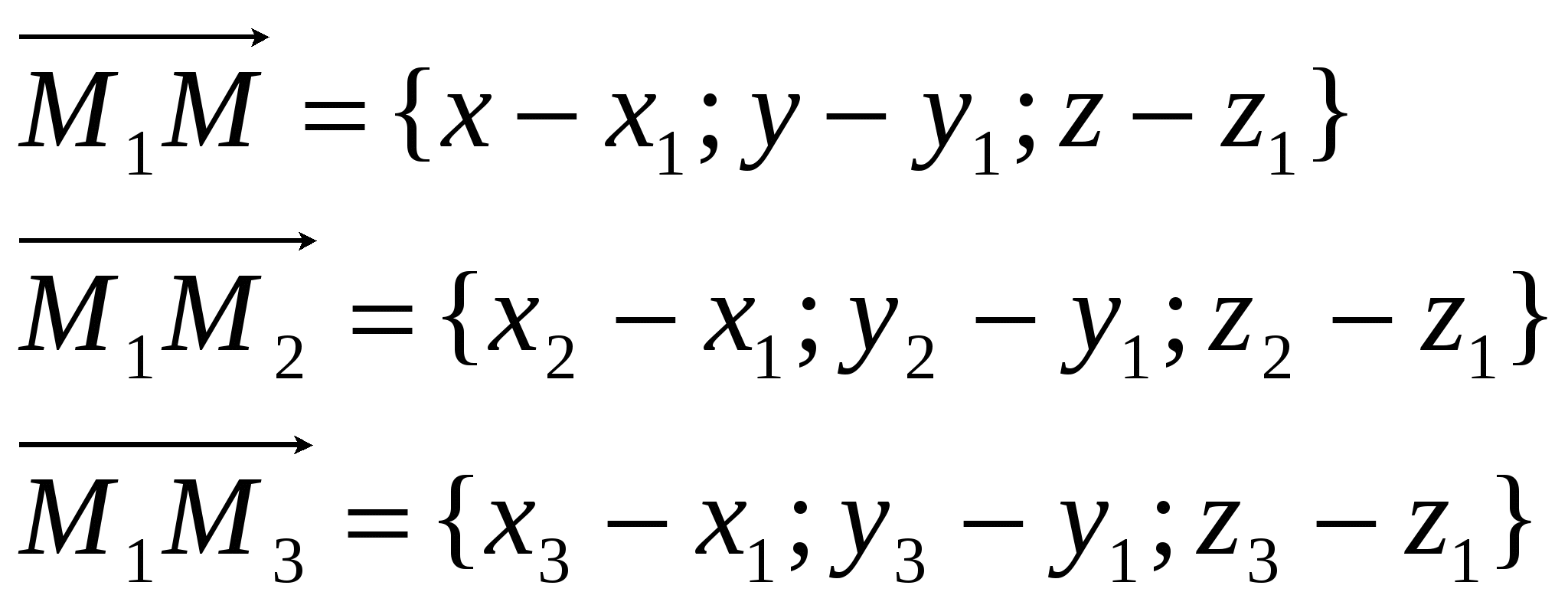
Уравнение плоскости, проходящей через три точки:
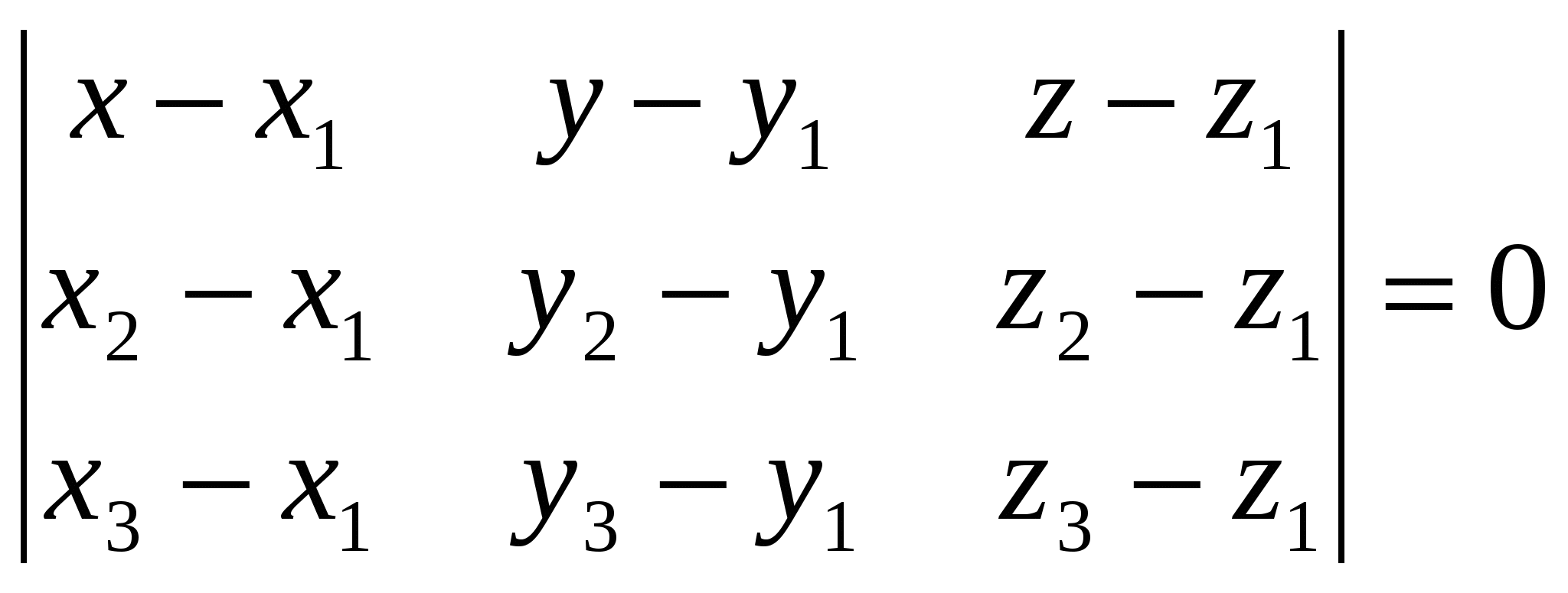
|
|
№ 20. Каждый не равный нулю вектор, лежащий на данной прямой или пар-ый ей, назыв направляющим вектором этой прямой. Направляющий вектор произвольной прямой обознач а, а его координаты l.m.n. а=( l.m.n). Если известна точка М0 (х0,у,z0) прямой и направляющий вектор а=(l.m.n), то прямая может быть определенна (двумя) уравнениями вида х-х0/ l = у-у0/ m = z-z0/ n – каноническое уравнение прямой. Канонич уравн прямой проход-ие через данные точки М1(х1,у1,z1) и М2(х2,у,z2) имеют вид х-х1/ х2-х1 = у-у1/у2-у1= z-z1/z2-z1. Обозначим буквой t каждое из равных отношений в канонических уравнениях получим х-х0/ l = у-у0/ m = z-z1/ n = t. Отсюда х= х0+lt, у=у0+mt z=z0+nt –это параметрические уравнения прямой, проходящей через точку М0 в направлении вектора а=(l.m.n).
|
|
№7. Опред линейного векторного пространства. Линейная комбинация векторов. Линейное векторное пространство это множество элементов произвольной структуры для которых заданы условия равенства и две операции, а именно сложение этих элементов и умножение на число. Св-ва: 1)для любых х и у принадлежащих v 2)? (λх) принадлежит v.
Линейная комбинация векторов. Вектор аm назыв линейной комбинацией векторов а1,а2,,,аm-1 векторного пространства R если он равен сумме произведений этих векторов на произведение действительного числа. аm= λ1а+ λ2а2,,,,+ λ m-1а m-1.
|
|
№21. Взаимное расположение L и П. 1) L׀׀ П следовательно n перпендикулярен П 2) L перпендикулярна П следовательно n ׀׀ а 3) L принадлежит П 4) L пересекает П=М
Угол между L и П. cosα=( n, а) / ׀ n׀ ׀а׀ =sin φ , где а- направляющий вектор. Расстояние от точки L до v3. Если прямая r=r1+at, где t параметр а-направляющий вектор, то h= S/ ׀а׀ = ׀ (r0-r1, a) ׀ S- площадь пар-ма построенного наь векторах r0- r и а, приведенных к общему началу.
|
|
№1. Матрицы, виды, действия с ними. Задачи.
№2.Определители квадратных матриц
№3.Обратная матрица. Критерии существования обр матрицы. Алгоритм вычислен обр матр.
№4. Умножение матриц. Транспонирование произведения матриц. Св-ва опред-ля от произведения матриц.
№5. Решение СЛАУ с помощью обратной матрицы.
№6. Определение геометрического вектора. Нулевой, противоположный вектор, коллинеарные и компланарные векторы. Равенство векторов.
№7. Опред линейного векторного пространства. Линейная комбинация векторов.
|
8.Линейная зависимость и линейная независимость векторов.
9.Определение базиса и размерности линейн.пространства.
10.Определение базисного минора матрицы. Лемма.Ранг.Вычисление ранга.
11. Системы линейных алгебраических уравнений (СЛАУ).Координатная и матричная формы записи.Равносильность СЛАУ.
12.Теорема Кринекера-Капелли о совместности СЛАУ.Решение СЛАУ с помощью обратной матрицы.Крамер.Гаусс.Критерий определен.слау
13.Решение однородных СЛАУ.Критерий существования ненулевого решения. Фундаментальная система.
|
14.Декартова прямоуг.система координат.Линейные операции над векторами.Вычисление длины вектора.
№15.Опр скал-ого произв-я. Его св-ва. Вывод формулы скал пр. Признак ортогональности векторов. Ортог проекция вект-а на ось.
№16.Правые и левые тройки геометр-их вект-ов. Опред вектор-ого произв-я.Его св-ва.Признак коллин-сти.
№17.Определение смешанного произведения трех векторов. Его св-ва. Признак компланарности 3 векторов. Нахождение объема тетраэдра.
№18. Уравнение прямой, проходящей через две данные точки. Уравнением прямой с угловым коэф-от. Уравнение прямой в отрезках.
|
№18 Уравнение прямой, проходящей через две данные точки. Взаимное расположение прямых на плоскости. Условия пар-сти и перпендикулярности прямых. Расстояние от точки до прямой. Нормальный вектор. Направляющий вектор. Каноническое уравнение. Параметрическое уравнение. Нормальное уравнение прямой на плоскости.
№19. Общее уравнение плоскости. нормальным вектором. общим уравнением плоскости. Условием пар-ости двух плоскостей. Нормальным уравнением плоскости. Расстояние от точки до плоскости. Уравнение плоскости проходящей через три точки. Уравнение плоскости проходящей через три точки.
каноническое уравнение прямой. параметрические уравнения прямой.
|
21.Взаимное расположение L и П. Угол между L и П.
Расстояние от точки L до v3.
22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. Определения,вывод их канонических ур-ий.Фокусы,эксцентриситет,директр.
23.Общие ур-ие кривых второго порядка на плоскости. Инварианты кривых второго порядка на плоскости.Классификация и виды каноническихь ур-ий(9)кривых второго порядка.
24.Поверхности второго порядка.Эллипсоиды,гиперболоиды,Параболоиды, цилиндры,конусы.Канонич.ур-я.Инварианты.
25.Линейные операторы в линейном пространстве. Матрица линейного оператора.
26.Преобразование координат вектора при переходе к новому базису. Изменение координат вектора при изменении базиса.
|
27.Собственные векторы и собственные значения линейного оператора. Характеристический многочлен линейного оператора.
| |
|
|
 Скачать 0.57 Mb.
Скачать 0.57 Mb.