|
|
МАТАН (шпоры). 8. Линейная зависимость и линейная независимость векторов. Векторы назыв коллинеарными,если лежат на
8.Линейная зависимость и линейная независимость векторов.
Векторы назыв.коллинеарными,если лежат на | |
прямых или на одной прямой.
Векторы назыв.компланарными,если они лежат на | | плоскостях или на одной плоскости.
Нулевой вектор считается коллинеарным любому другому вектору. Нулевой вектор считается компланарным любой паре векторов. Векторы 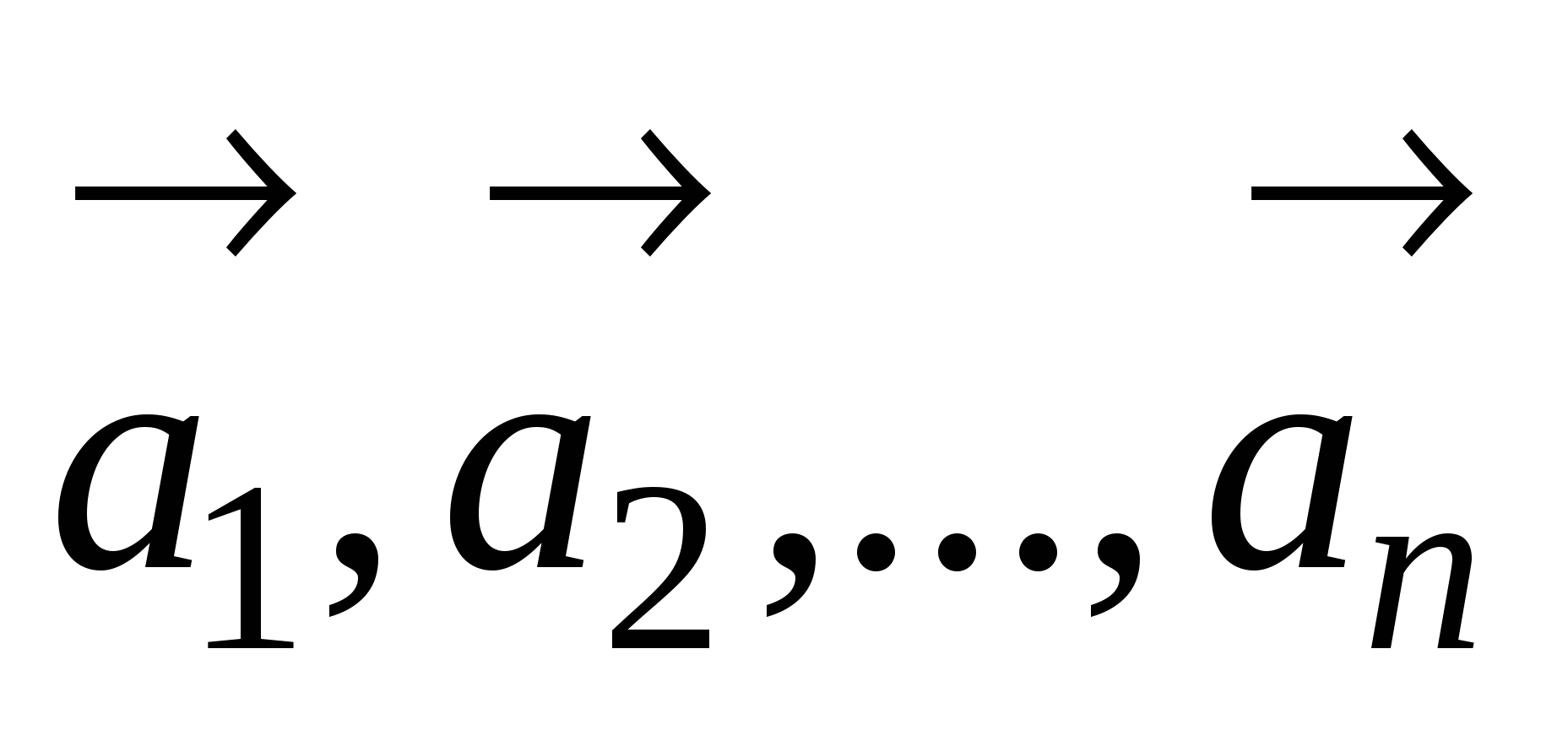 называются линейно зависимыми, если существует такой набор коэффициентов называются линейно зависимыми, если существует такой набор коэффициентов
из которых хотя бы один отличен от нуля, т.е.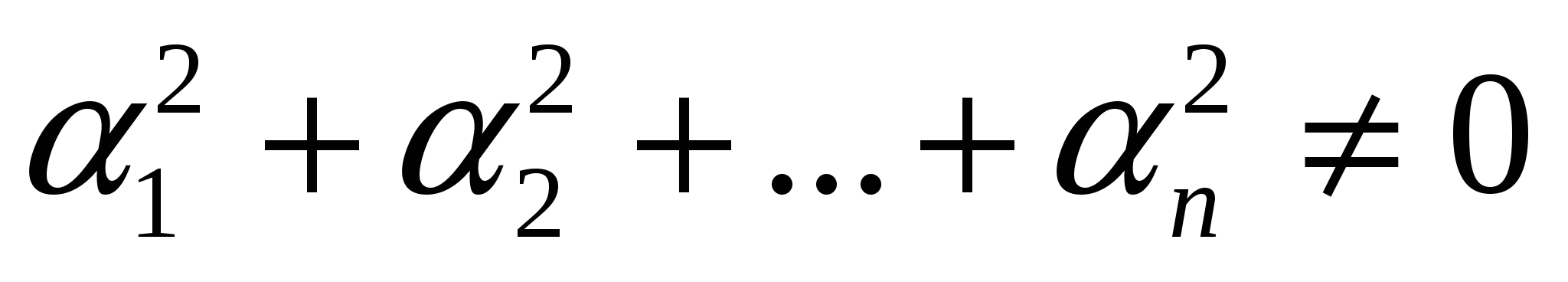
В ектор an назыв.линейн.комбинацией векторов ектор an назыв.линейн.комбинацией векторов 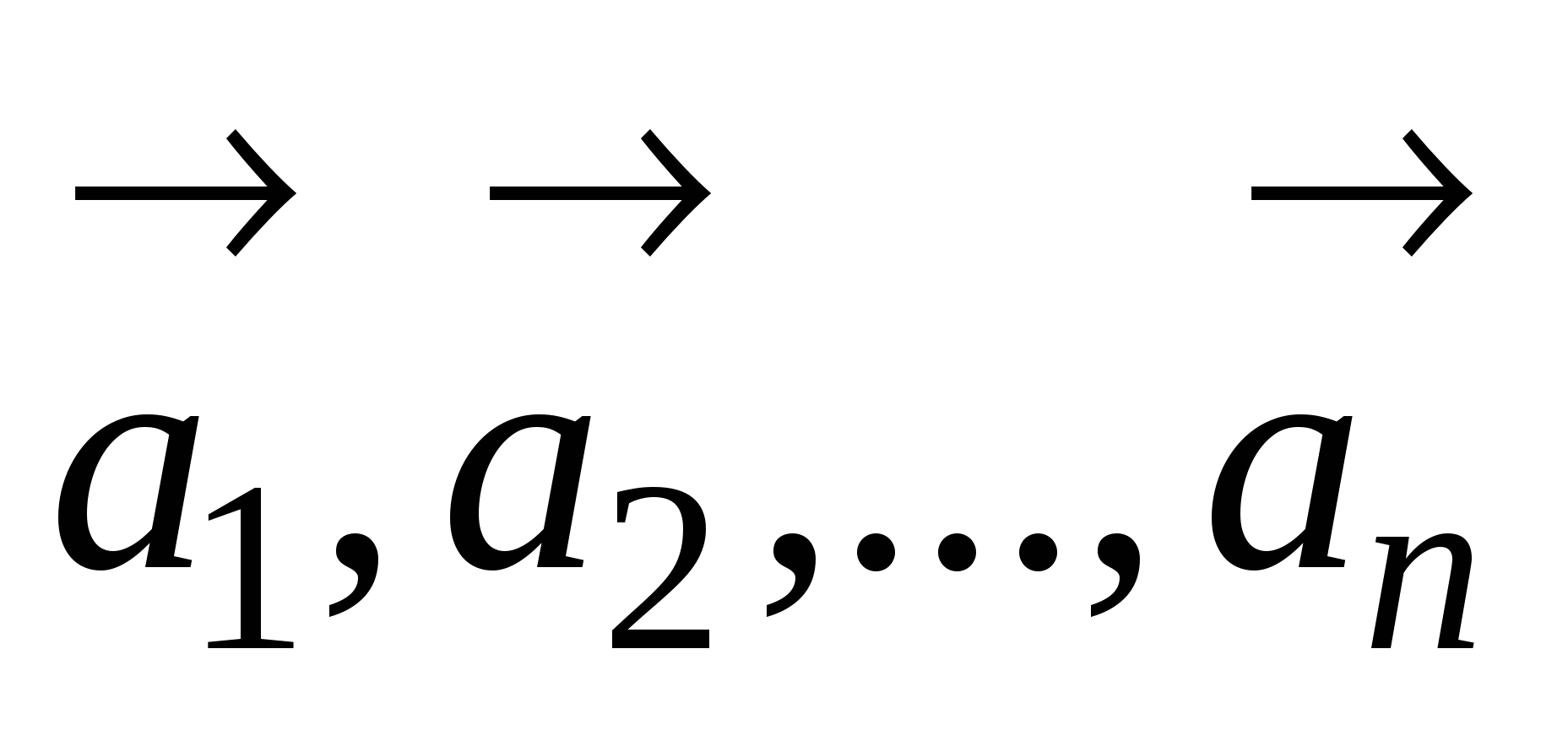 ,векторного пространства R,если он равен сумме произведений этих векторов на произвольн.числа. ,векторного пространства R,если он равен сумме произведений этих векторов на произвольн.числа. 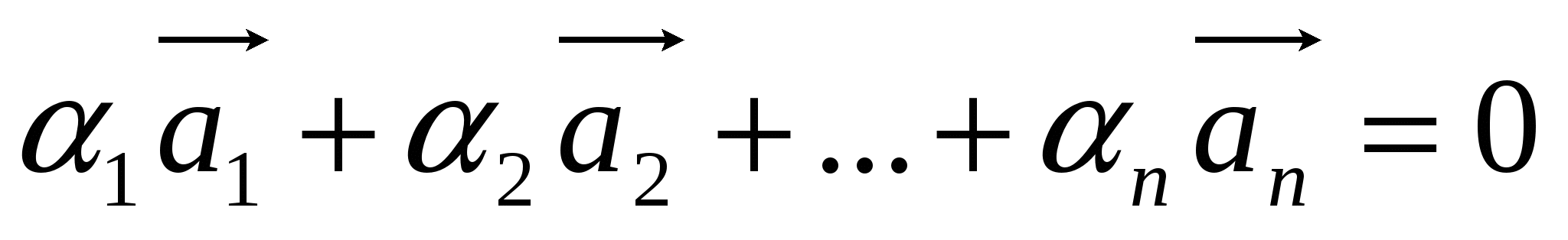
|
Система векторов называется линейно независимой,если равенство 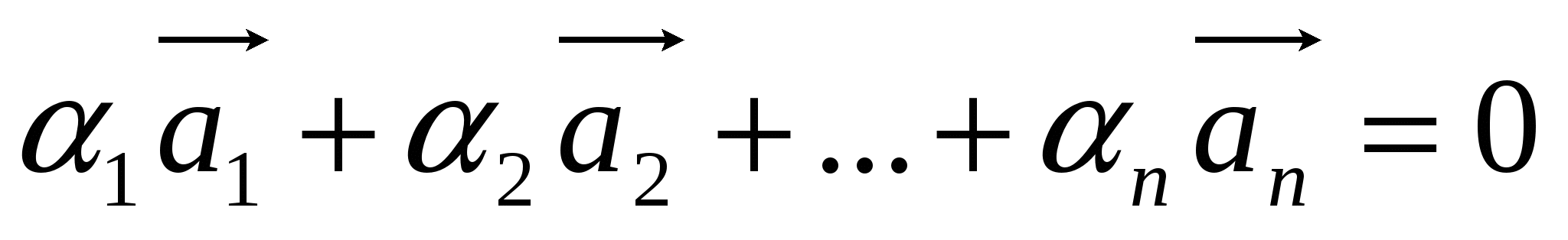 ,возможно только при ,возможно только при
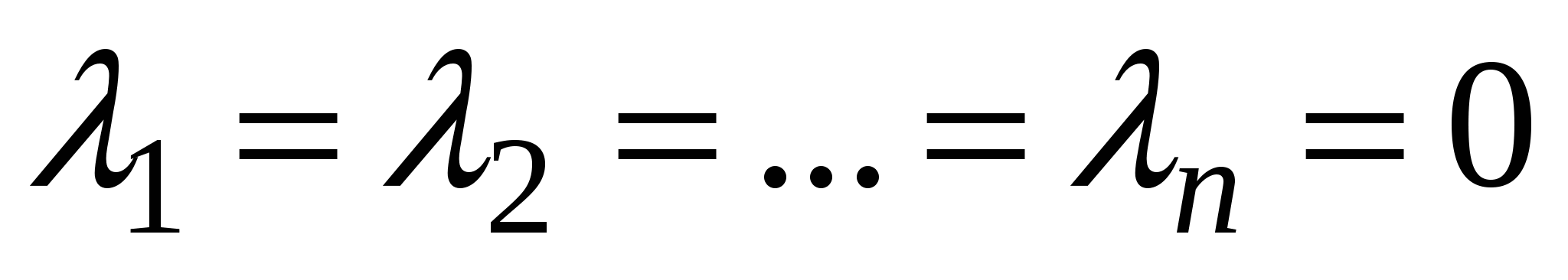 . .
Критерий. Для линейной зависимости векторов 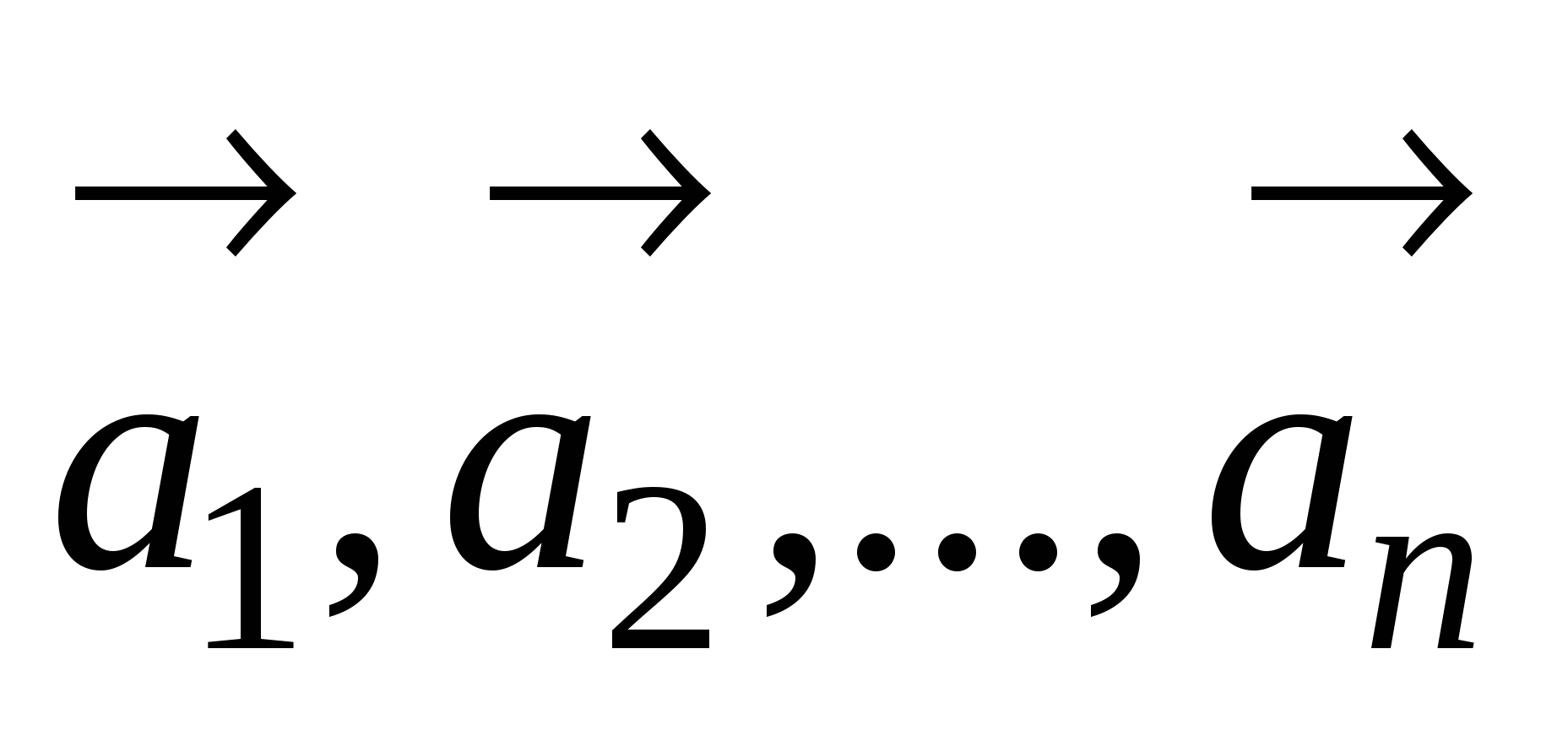 , необходимо и достаточно, чтобы один из них был линейной комбинацией остальных. , необходимо и достаточно, чтобы один из них был линейной комбинацией остальных.
Св-ва: 1.Если среди векторов имеется нулевой вектор,то эти векторы линейно независимы.
2.Если часть векторов являются линейно зависимыми,то все эти векторы-линейно зависимые.
1.Один вектор линейно независим тогда и только тогда, когда он ненулевой. 2.Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны.3.Три вектора линейно независимы тогда и только тогда, когда они некомпланарны.
|
|
9.Определение базиса и размерности линейн.пространства.
Базисом в пространстве называется любая упорядоченная тройка линейно независимых векторов.
n-мерным пространством назыв.упорядоченная совокупность n действительных чисел,записываемых в виде X=(X1,X2...Xn),где
Xi-i-я компонента вектора X.
1.x+y=y+x-коммутативное св-во суммы
2.(x+y)+z=x+(y+z)-ассоциативное(сочетательное)
3. ассоциативное относительно числового множителя св-во
4. дистрибутивное(распределит.)
относительно суммы векторов св-во
5. дистрибутивное относит.суммы
|
числовых множителей св-во
6.Существует нулевой вектор 0=(0,0,…0) такой, что х+0=х для любого вектора х
7. Для любого вектора х существует противопол.
Вектор(-х) такой,что х+(-х)=0
8.1*х=х для любого вектора х(особая роль числового множителя 1).
Множество векторов с действительн.компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее 8 св-ам,назыв.векторным пространством.
Линейное пространство R назыв.n-мерным,если в
нём существует n линейно независимых векторов,
а любые из (n+1)векторов уже явл.зависимыми.
|
|
9.Определение базиса и размерности линейн.пространства.
Размерность пространства-это максим.число содержащихся в нём линейно независимых векторов. Число n назыв.размерностью пространства R и обозначается dim(R). Совокупность n линейно независимых векторов n-мерного пространства R назыв.базисом.Скалярным произведением двух векторов X=(X1,X2,...Xn) и Y=(Y1,Y2,...Yn)называется число (X,Y)=X1Y1+X2Y2+...+XnYn=
Св-ва скалярного произведения:
1.(x,y)=(y,x)-коммутативное св-во
2.(x,y+z)=(y,x)+(x,z)- дистрибутивное
3.
4.(x,x)>0,если х-ненулев.вектор;(х,х)=0,если х-нулевой вектор.
|
Линейное(векторное)пространство,в котором задано скалярное произведение векторов, удовлетв.4ем св-ам,назыв.евклидовым пространством.Длиной(нормой)вектора х в евклид.пространстве назыв.корень квадратный из его скалярного квадрата:|x|=…
Св-ва:1.|x|=0 тогда и т.т.,к. х=0 2.
3.|(x,y)| |x||y| 4.|x+y| |x|+|y| (неравенство тр-ка).
Два вектора называются ортогональным,если их скалярное произведение равно нулю.
Векторы l1,l2,...ln n-мерного евклид.пространства
Образуют ортонормированный базис,если эти векторы попарно ортоганальны и норма каждого из них равна единицы,т.е.если (li,lj)=0 при i j и |li|=1 при i=1,2,...n.
|
|
9.Определение базиса и размерности линейн.пространства. Пусть дан базис 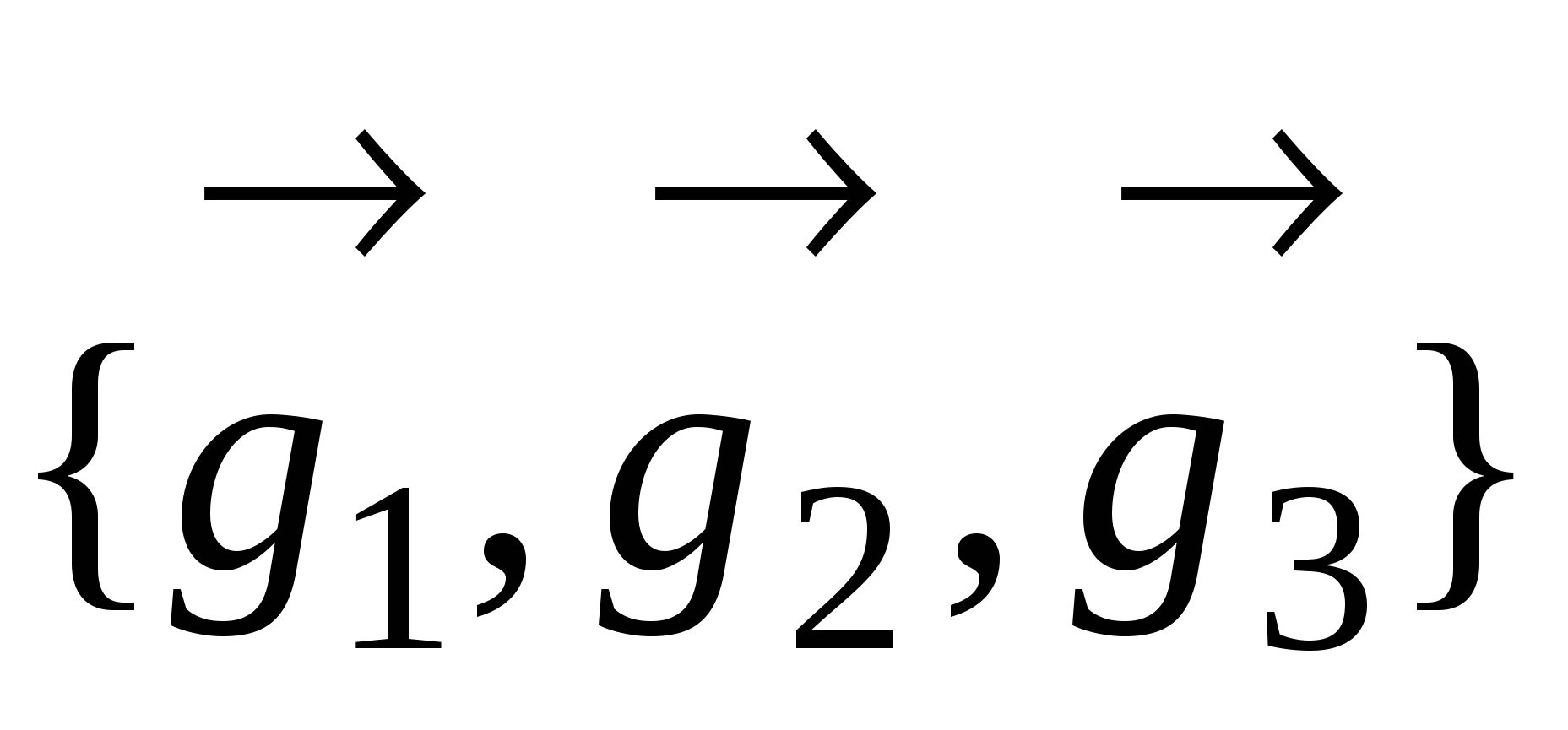 , тогда любой вектор , тогда любой вектор 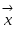 в пространстве может быть представлен, и притом единственным образом, в виде в пространстве может быть представлен, и притом единственным образом, в виде 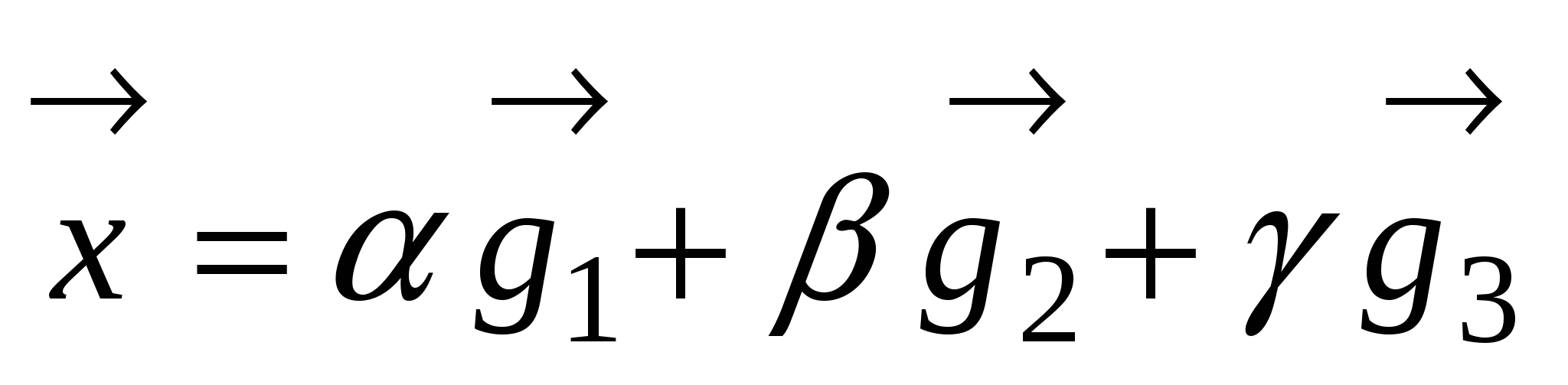 , где , где 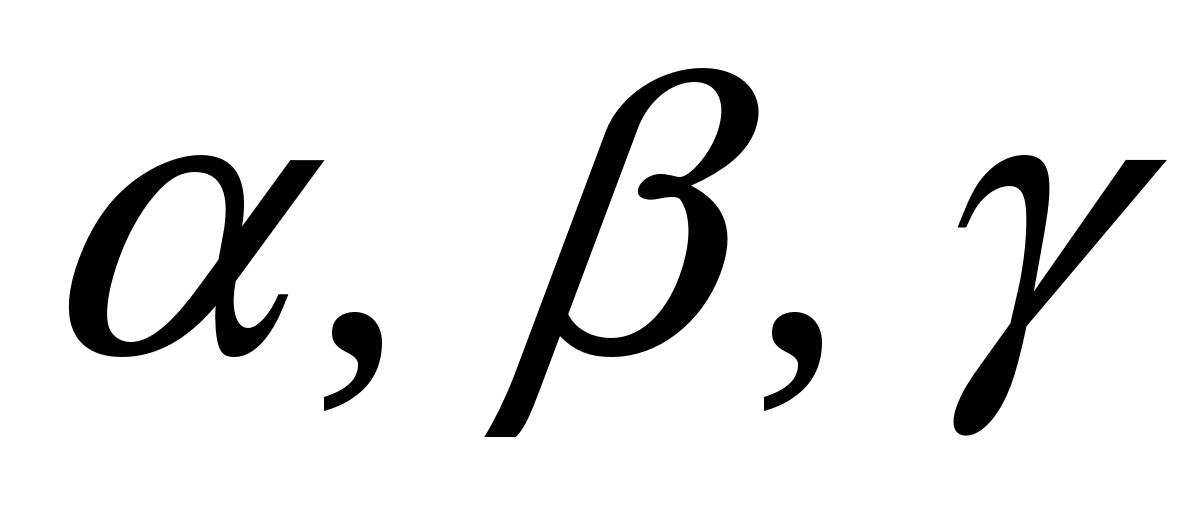 - некоторые числа. Совместим начала всех векторов - некоторые числа. Совместим начала всех векторов 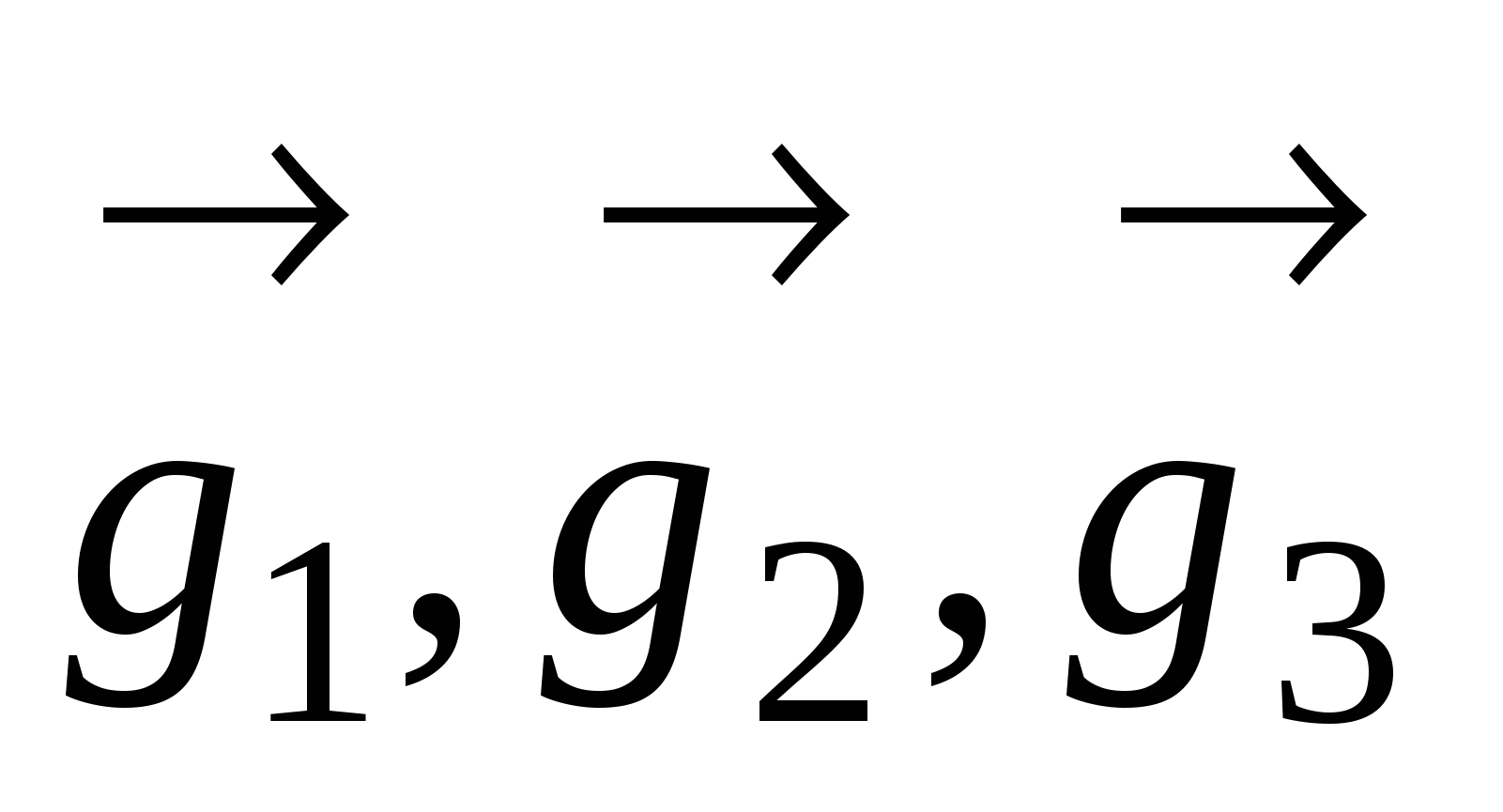 и и 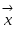 в точке O и проведем через конец вектора в точке O и проведем через конец вектора 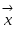 плоскость, параллельную плоскости плоскость, параллельную плоскости 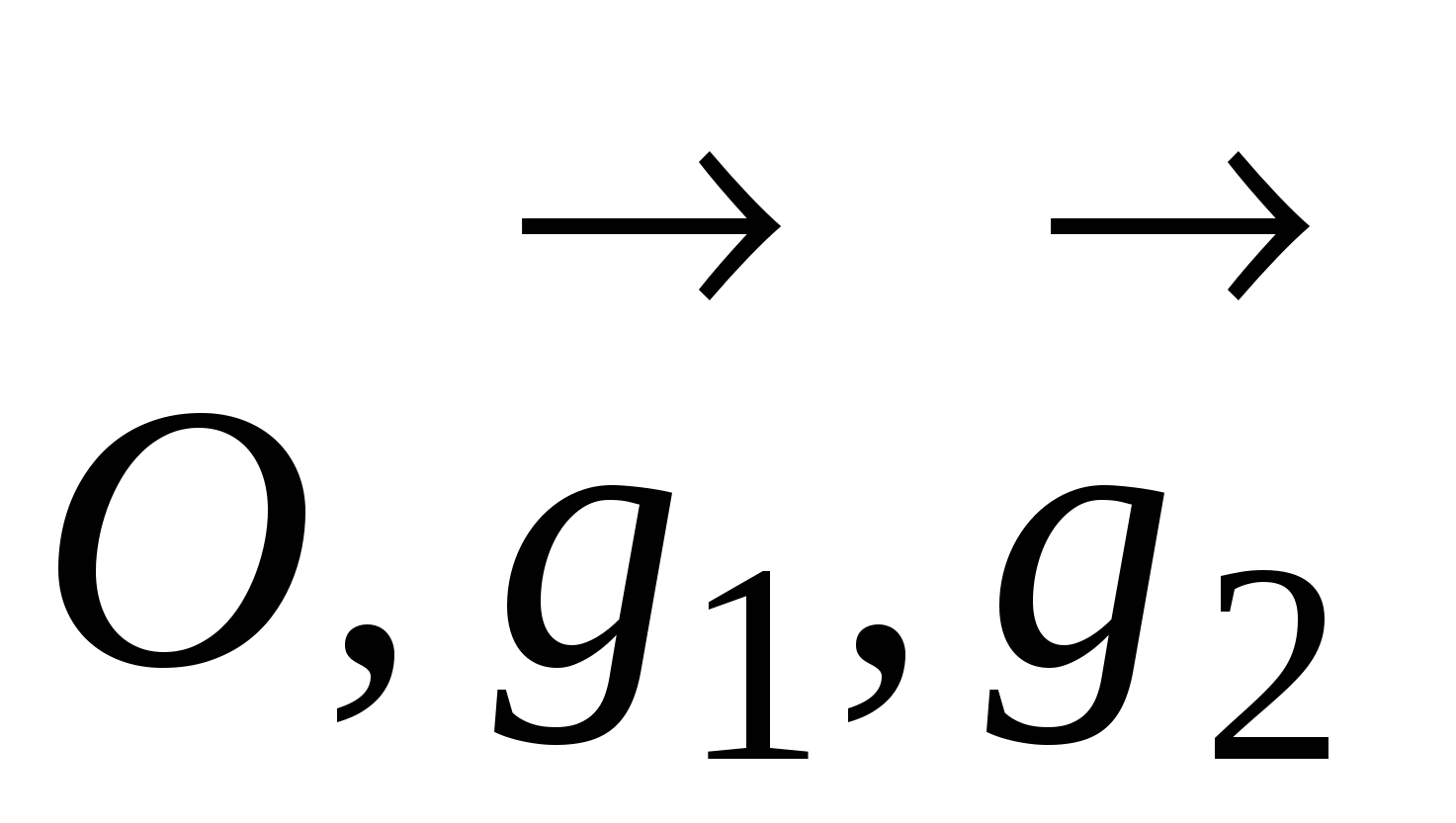 . .
|
Построим новые векторы 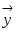 и и 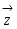 так, чтобы так, чтобы 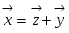 , а , а 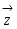 и и 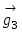 были коллинеарны, тогда, в силу коллинеарности вектора были коллинеарны, тогда, в силу коллинеарности вектора 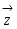 вектору вектору 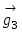 , , 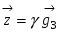 . Перенеся начало вектора . Перенеся начало вектора 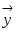 в точку O и рассуждая как при доказательстве теоремы 1.4.3., получим в точку O и рассуждая как при доказательстве теоремы 1.4.3., получим 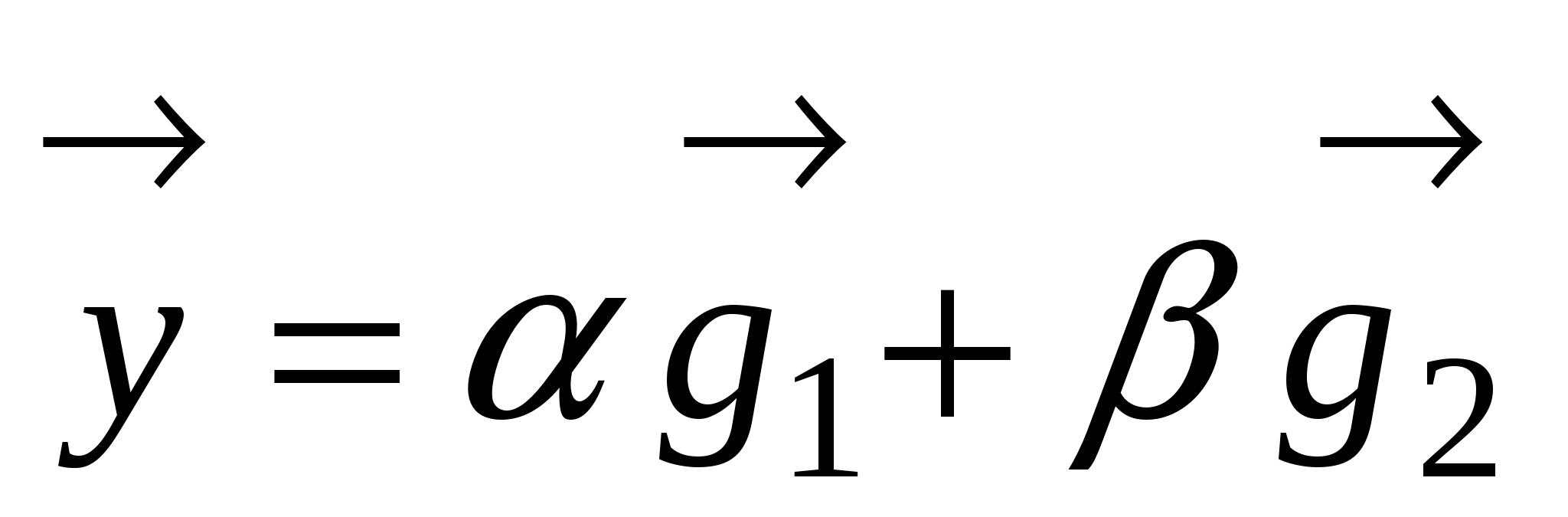 и, следовательно, и, следовательно, 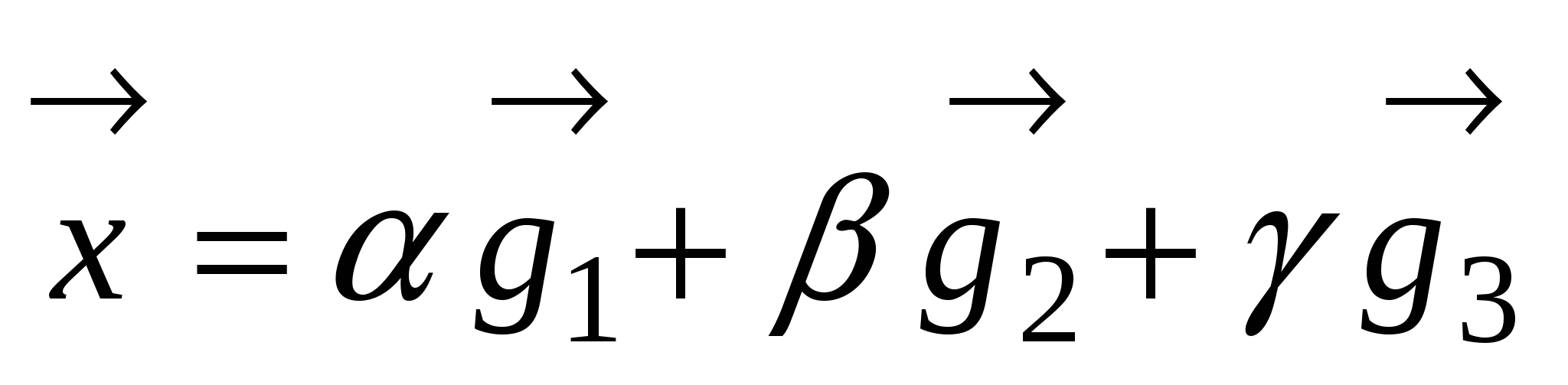 , что и доказывает существование разложения. , что и доказывает существование разложения.
|
|
9.Определение базиса и размерности линейн.пространства.
Числа 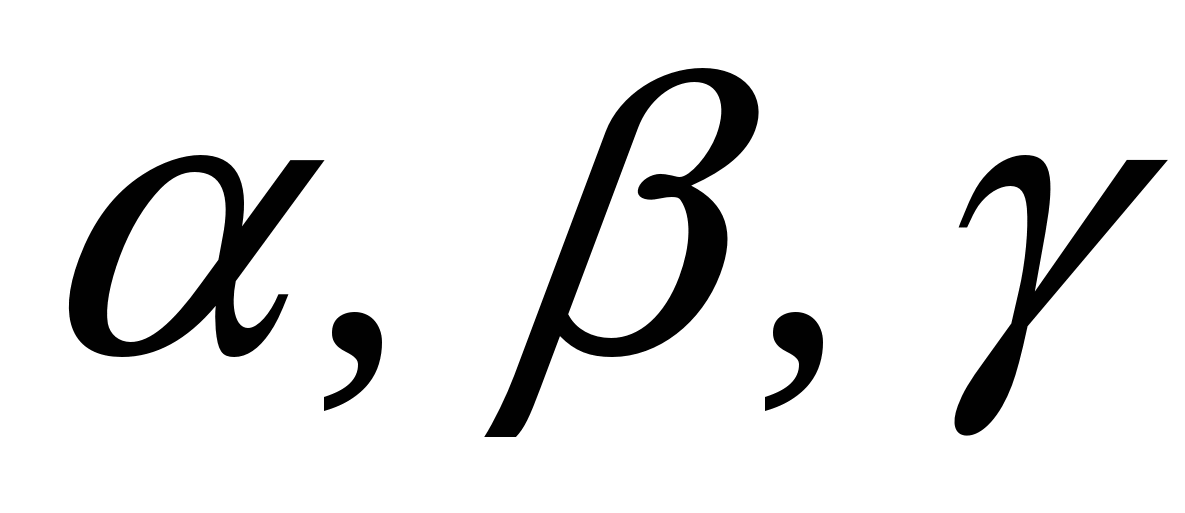 - коэффициенты в разложении - коэффициенты в разложении 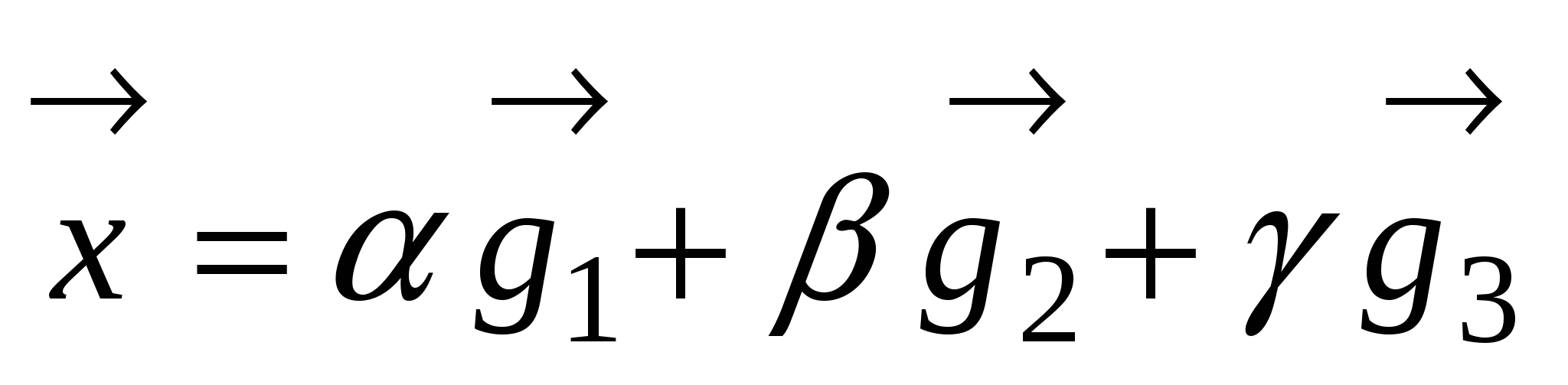 , называются координатами (или компонентами) вектора , называются координатами (или компонентами) вектора 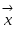 в базисе. Для записи вектора в базисе. Для записи вектора 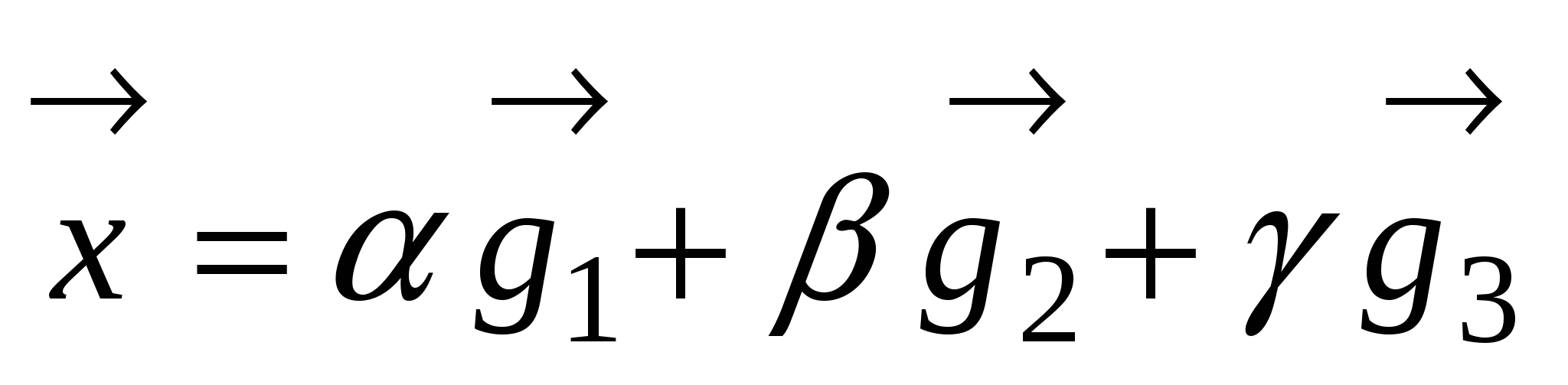 в координатном представлении используются формы: в координатном представлении используются формы:
1.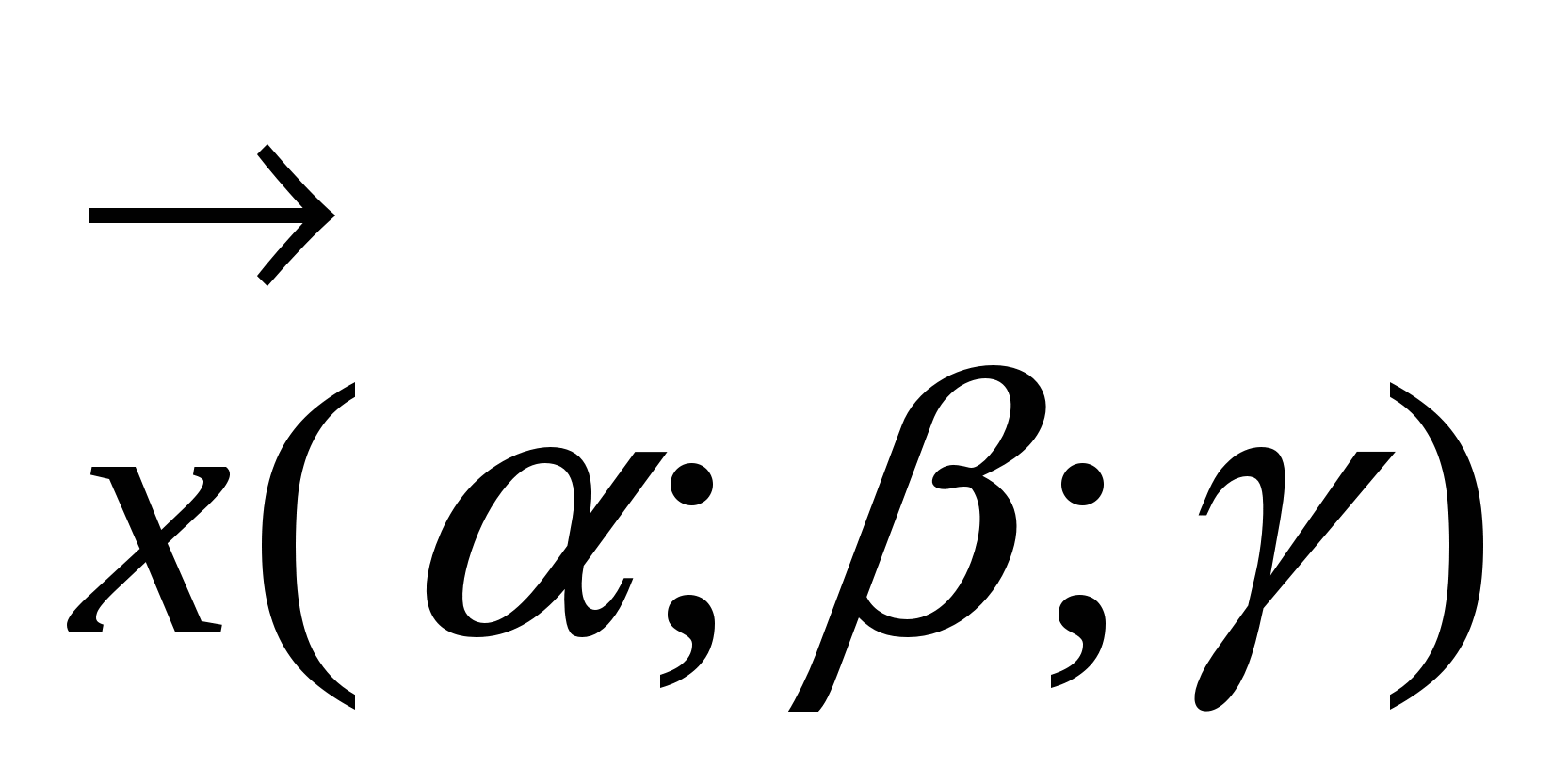 2. 2.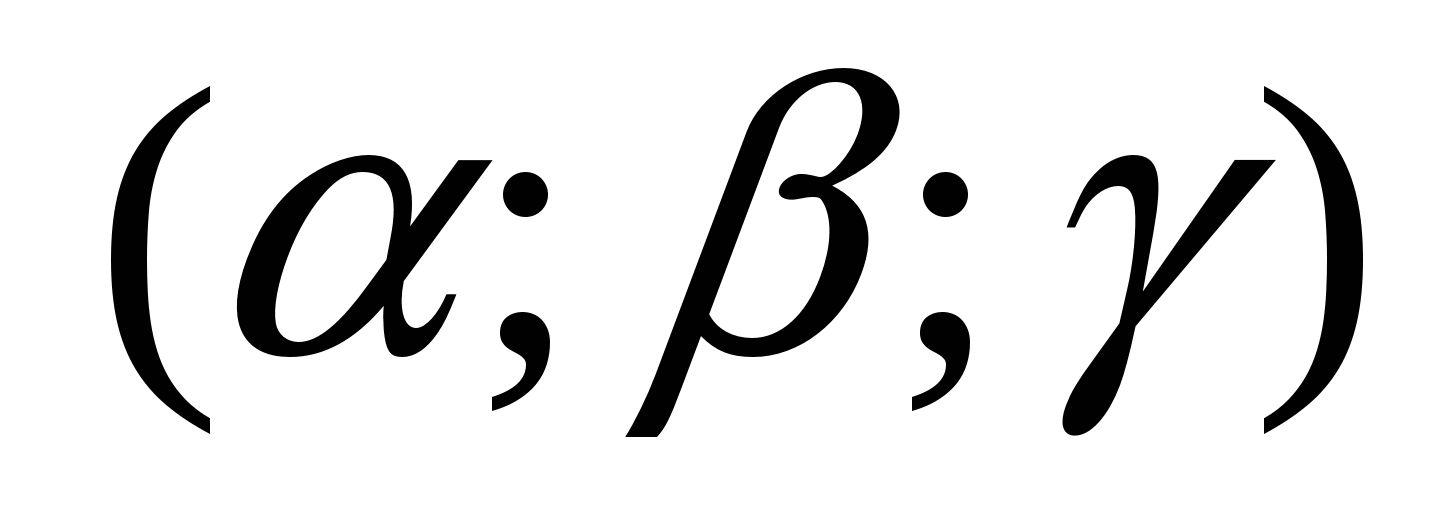 3. 3. 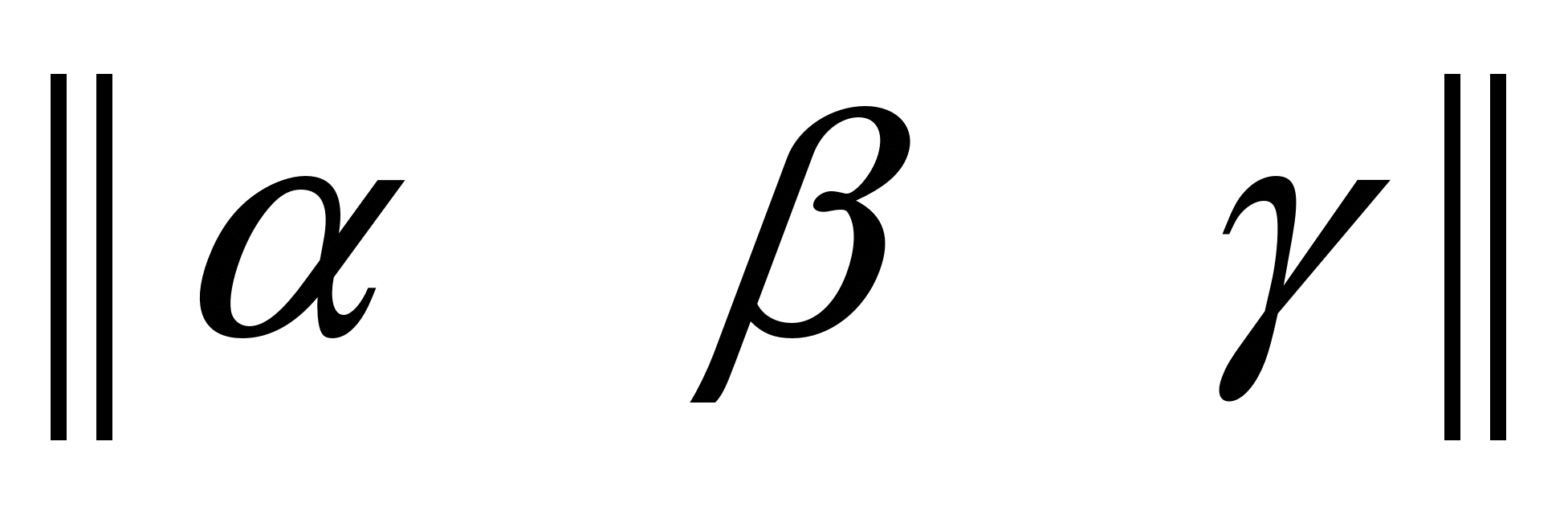
|
В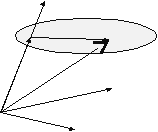 общем случае утверждение "вектор общем случае утверждение "вектор 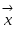 в базисе в базисе 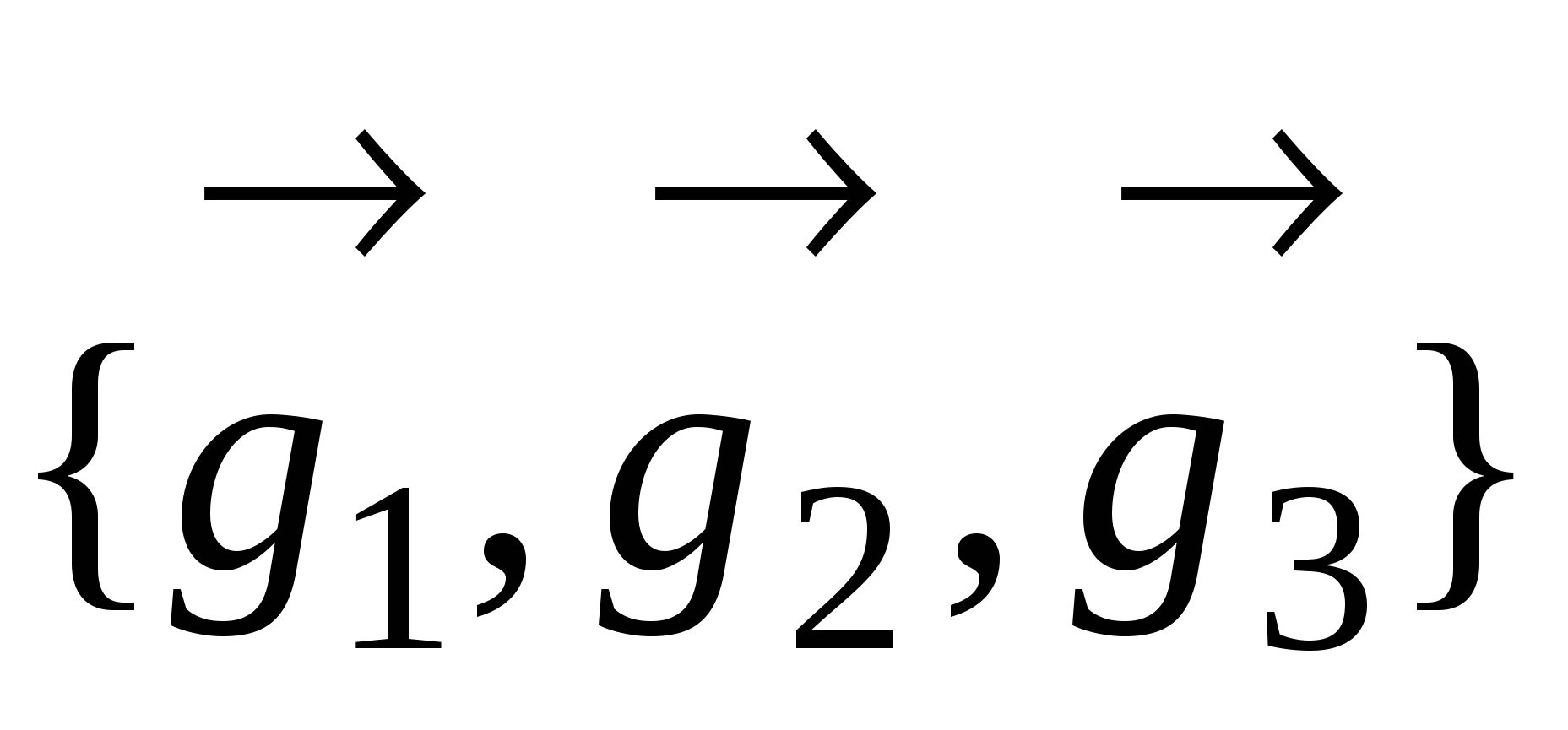 имеет координатное представление имеет координатное представление 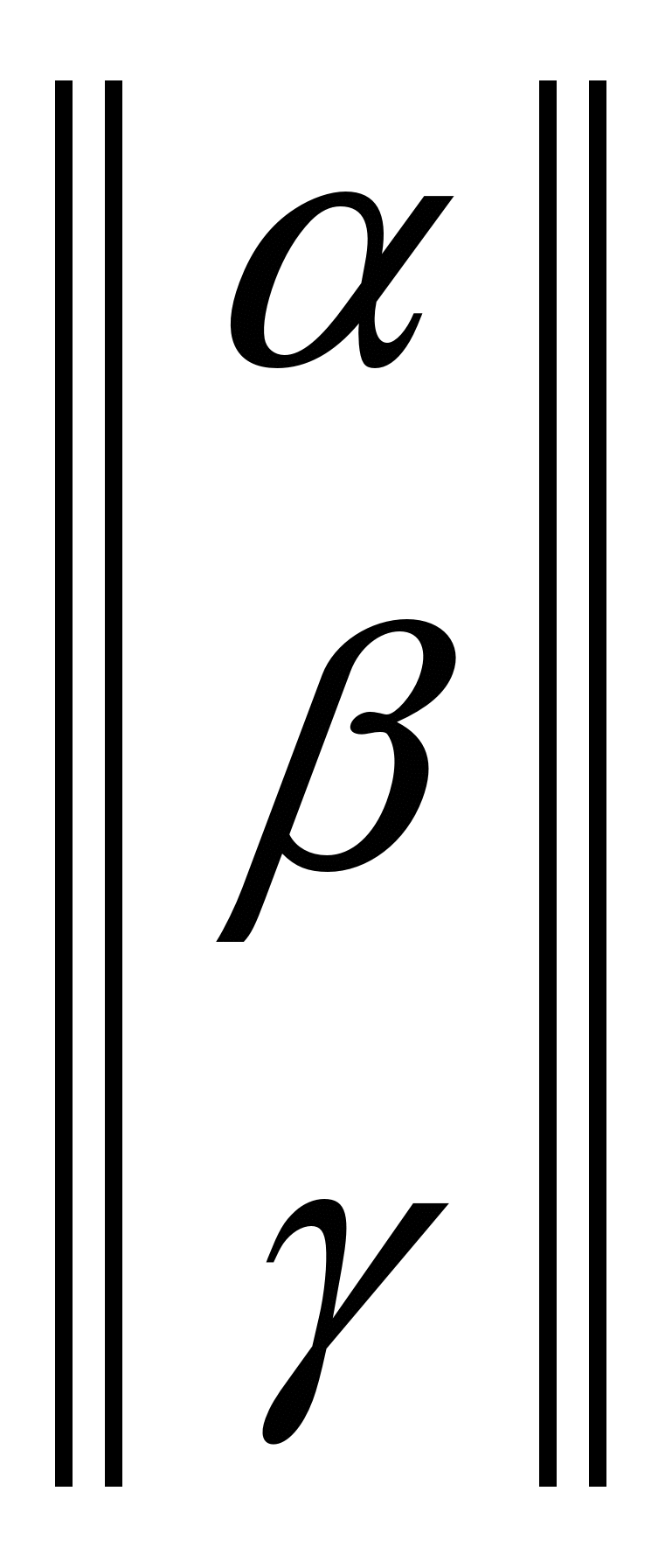 " записывается как " записывается как 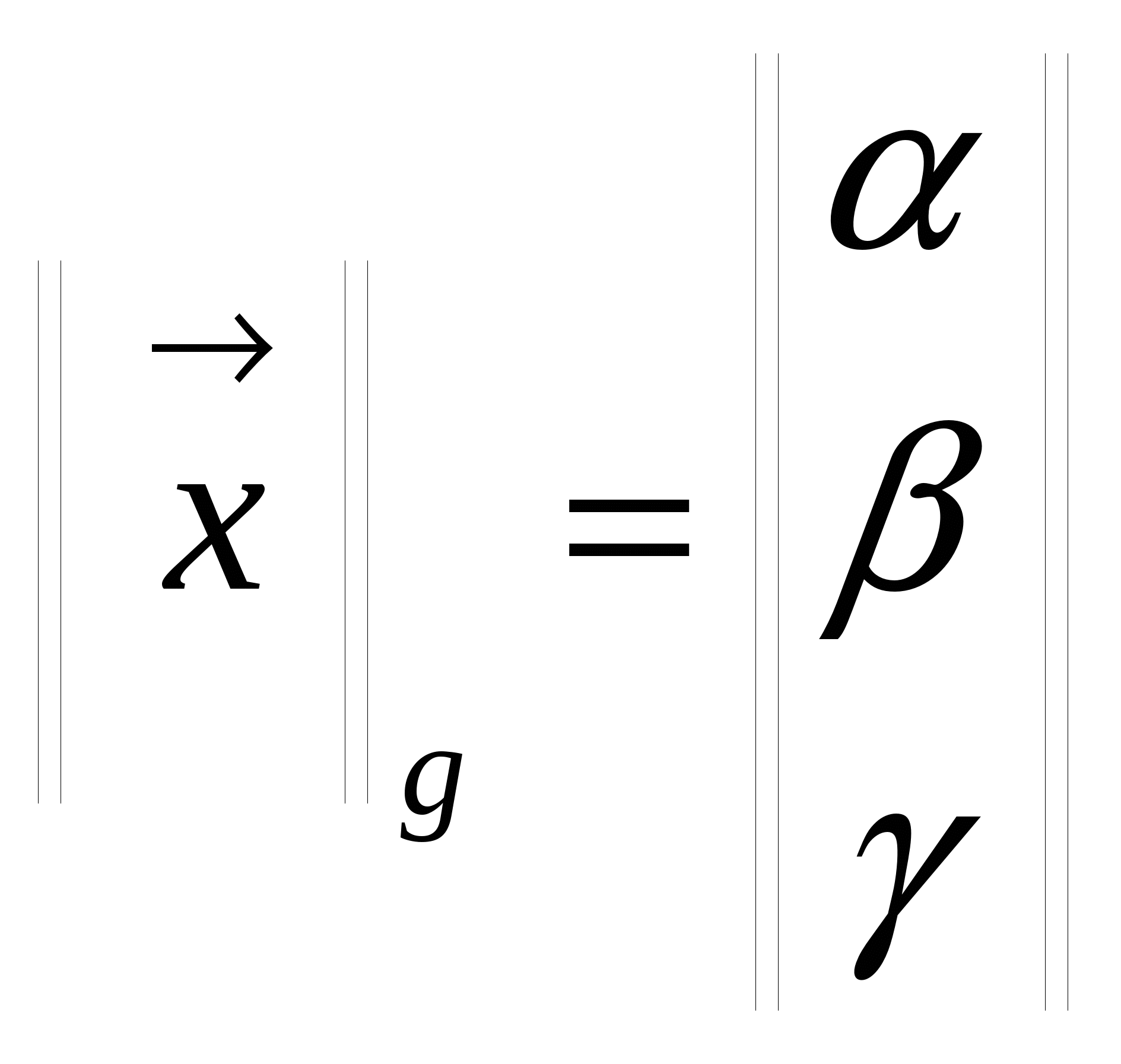 . . 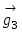
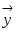
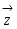 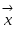 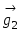
О
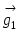
|
|
10.Определение базисного минора матрицы. Лемма.Ранг.Вычисление ранга.
Матрицей размера mxn называется упорядоченная прямоугольная таблица (или массив) чисел, содержащая m строк и n столбцов. Минором Mij элемента aij матрицы n-го порядка назыв.определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.Базисным минором матрицы называется любой её ненулевой минор максим. порядка.Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю.Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.
|
Теорема о базисном миноре.В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор. Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.Если А- квадратная матрица и detA = 0, то по крайней мере один из столбцов – линейная комбинация остальных столбцов. То же самое справедливо и для строк. Данное утверждение следует из свойства линейной зависимости при определителе равном нулю.
Если 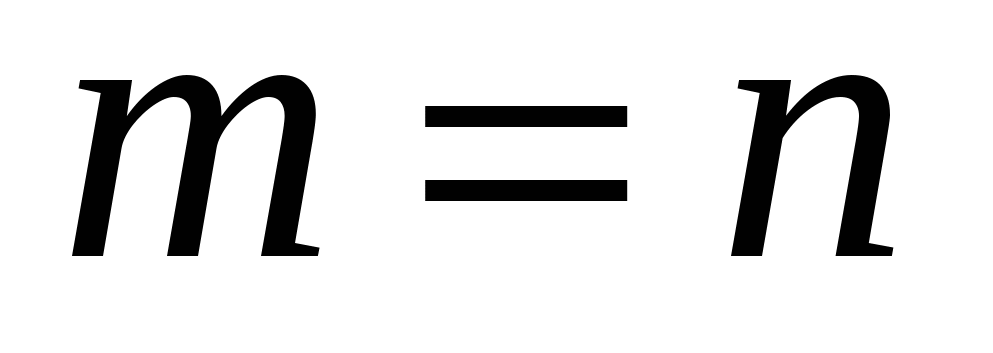 , то матрица называется квадратной, порядка n . , то матрица называется квадратной, порядка n .
Рангом матрицы А назыв.наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы А обознач.rang A или r(A).1)ранг матрицы Аm*n не превосходит меньшего из её размеров, т.е.
r(A) min(m,n).2)r(A)=0тогда,кога все элементы матрицы равны нулю,т.е. A=0. 3)для квадратной
|
|
10.Определение базисного минора матрицы. Лемма.Ранг.Вычисление ранга.
матрицы n-го порядка r(A)=n тогда и т.т.к. матрица А-невырожденная.Невырожденная матрица ― квадратная матрица, определитель которой отличен от нуля
Элементарные преобразование матрицы:
1.Отбрасывание нулевой строки(столбца)
2.Умножение всех элементов строки(столбца) матрицы на число,не равное нулю.
3.Изменение порядка строк(столбцов) матрицы
4.Прибавление к каждому элементу одной строки
(столбца) соответствующих элементов другой строки(столбца),умноженных на любое число.
5.Транспонирование матрицы.
Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
|
Рангматрицы-кол-во ненулевых строк ступенчатой матрицы,которые получаются из исходной с помощью элементарных преобразований.
|
|
11. Системы линейных алгебраических уравнений (СЛАУ).Координатная и матричная формы записи.Равносильность СЛАУ.
Система m уравнений с n неизвестными в общем виде записывается следующим образом:
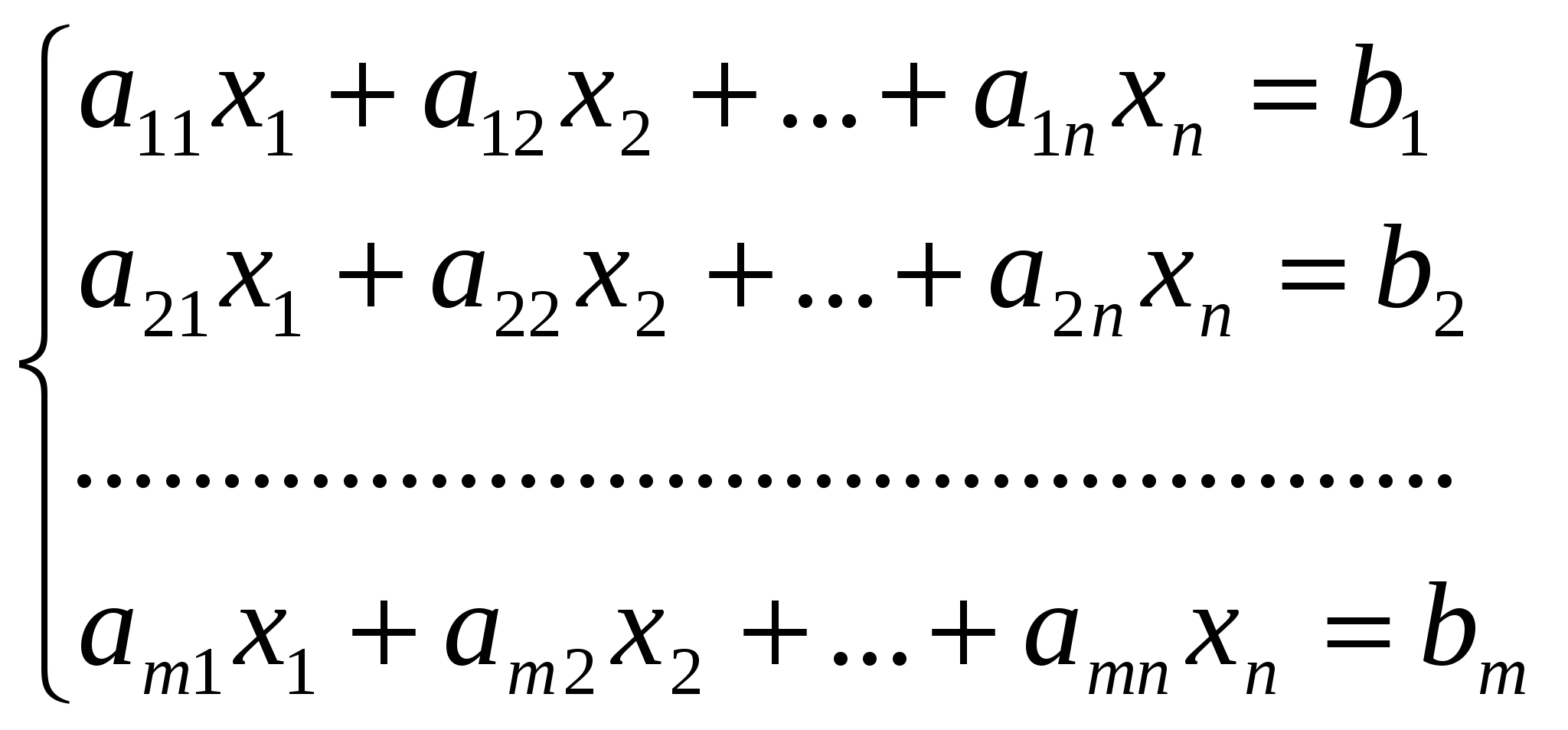
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.
Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
|
Система называется определенной, если она имеет только одно решение и неопределенной, если более одного. Матрица 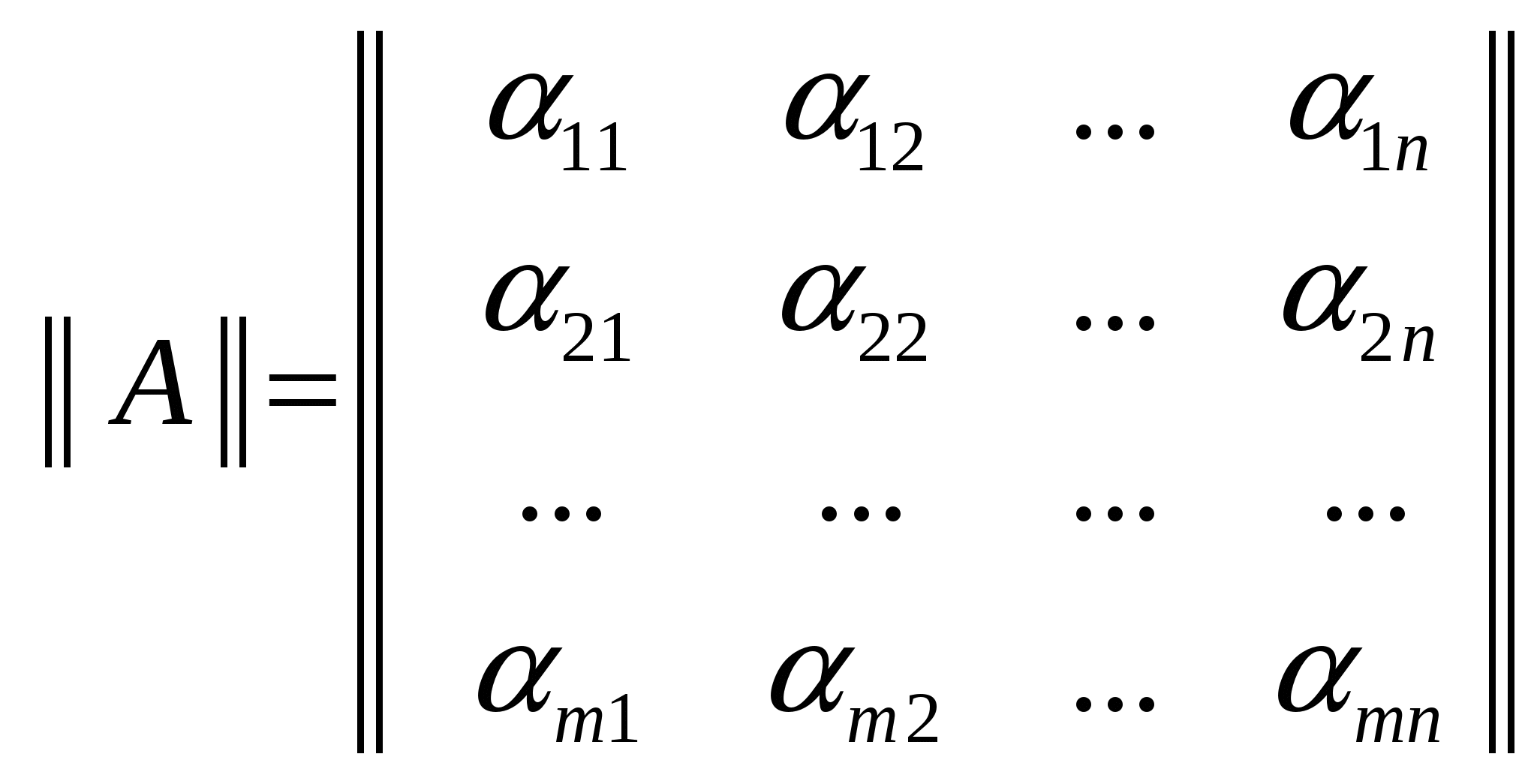 называется основной матрицей системы, а матрица называется основной матрицей системы, а матрица 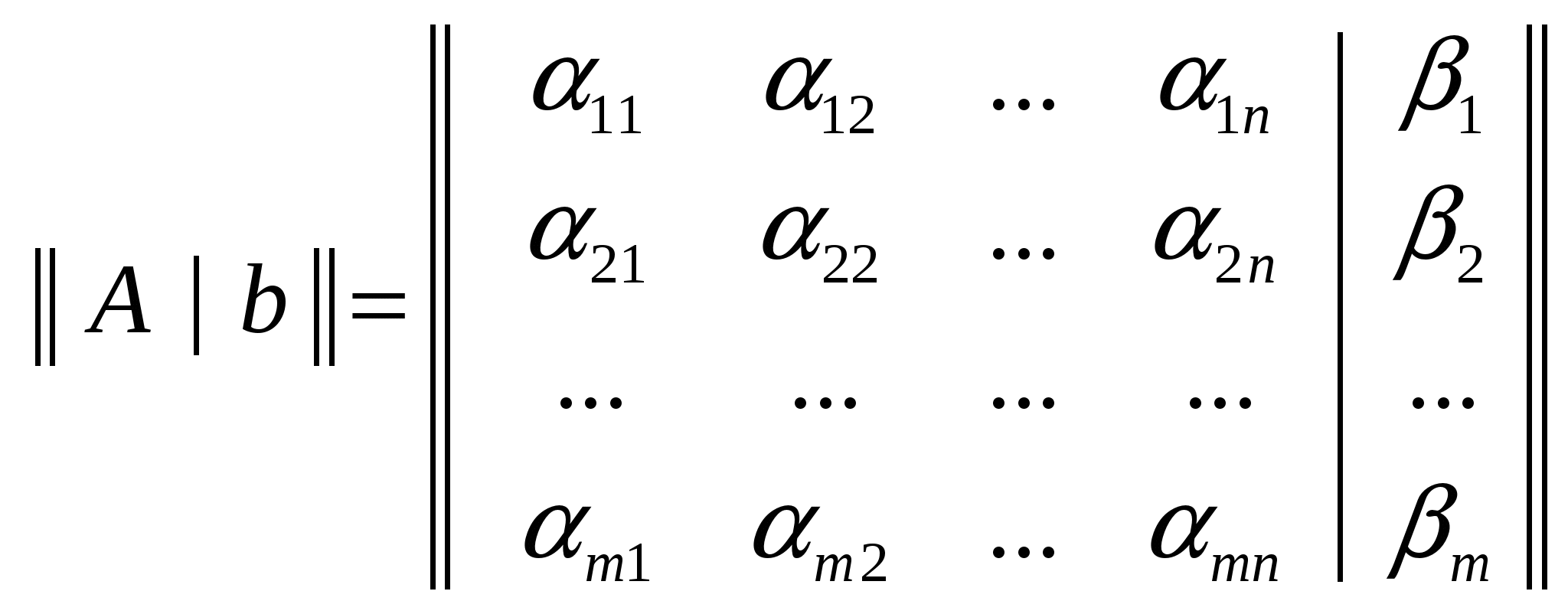 - расширенной матрицей этой системы. - расширенной матрицей этой системы.
|
|
11. Системы линейных алгебраических уравнений (СЛАУ).Координатная и матричная формы записи.Равносильность СЛАУ.
Однородная система уравнений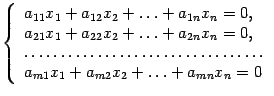
всегда является совместной. Для этой системы набор чисел Х1=0,Х2=0…Хn=0 является решением. Рассмотрим неоднородную систему m линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn:
В отличие от однородной системы, эта система совместна не всегда.
Справедливо утверждение (теорема Кронекера-Капелли).
|
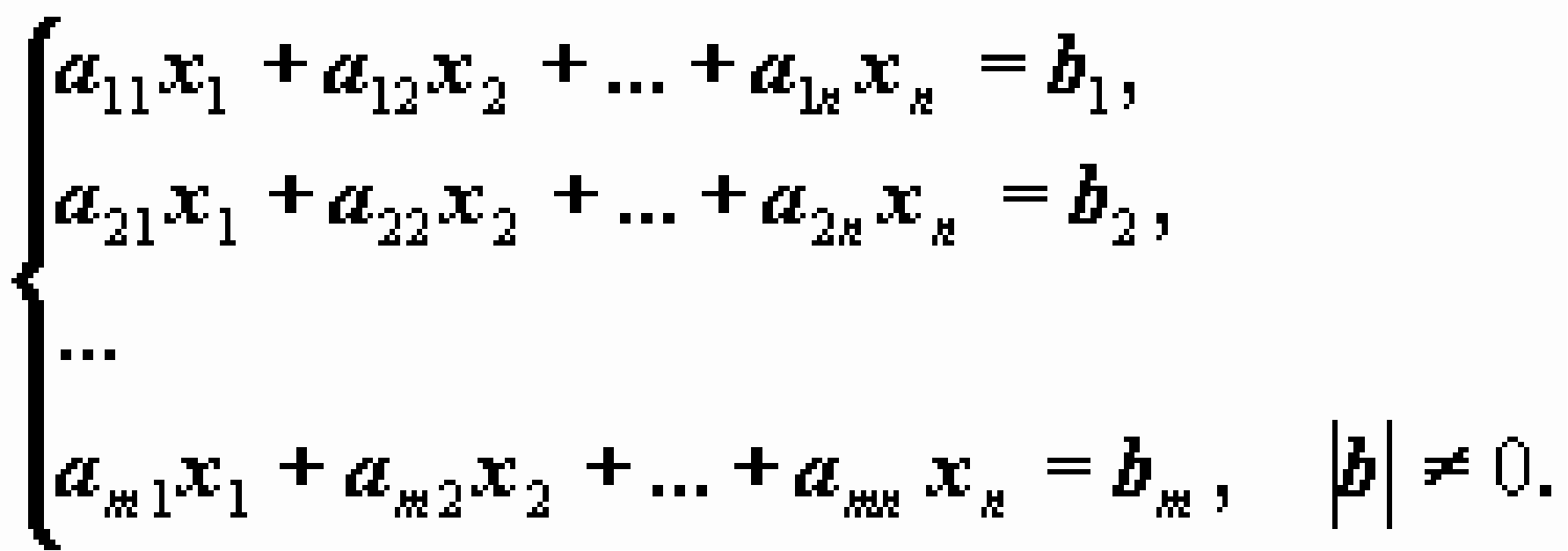
Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы. Исследовать неоднородную систему — это значит установить, является ли она совместной, и если является — найти выражение для общего решения системы.
Две системы равносильны (или эквивалентны), если у них одно и то же множество решений: любое решение первой системы является решением второй и любое решение второй является решением первой.
|
|
12.Теорема Кринекера-Капелли о совместности СЛАУ.Решение СЛАУ с помощью обратной матрицы.Крамер.Гаусс.Критерий определен.слау
Теорема Кронекера-Капелли: Система линейных уравнений совместна тогда и только тогда.когда ранг матрицы системы равен рангу расширенной матрицы этой системы. RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1 + x2 + x2  + … + xn + … + xn 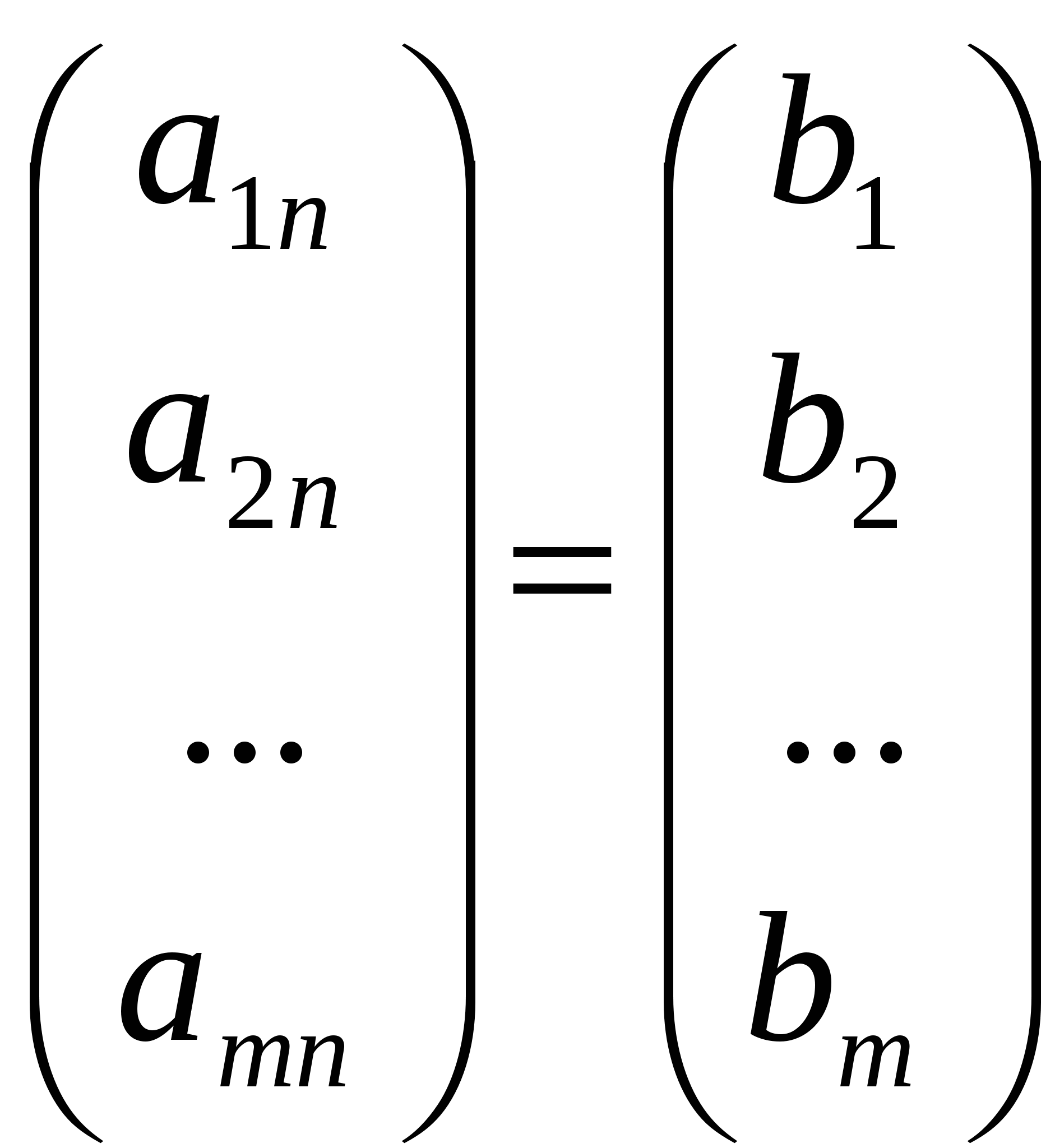
|
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.базисн.минор(билет10).
Для совместных систем линейных ур-ий равны следующие теоремы:1.Если ранг матрицы совместн.системы равен числу переменных,т.е. r=n, то система имеет единственное решение.
2.Если ранг матрицы совместной системы меньше числа переменных,т.е. r
|
| |
|
|
 Скачать 0.57 Mb.
Скачать 0.57 Mb.