МАТАН (шпоры). 8. Линейная зависимость и линейная независимость векторов. Векторы назыв коллинеарными,если лежат на
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
| 12.Теорема Кронекера-Капелли о совместности СЛАУ.Решение СЛАУ с помощью обратной матрицы.Крамер.Гаусс.Критерий определен.слау н  еопределенная и имеет бесконечное множество решений. еопределенная и имеет бесконечное множество решений. R Системы Сис-ма неопредел.    Зависимые несовместная (множ.реш.) Зависимые несовместная (множ.реш.)Система m Л    инейных инейныхУравнений с n Пременными R=m ур-ия r(A)=r(A1)=r r=n Сис-ма  Системы Сис-ма определенная Системы Сис-ма определеннаянезависим. Совместная ( 1 решение) | Решение СЛАУ с помощью обратной матрицы. Д  ля получения системы при m=n в общем виде предположи,что квадратн.матрица системы An*m невырожденная,т.е.её определитьель |A|=0.В этом случае существ.обратная матрица. Умножая слева обе части матричного равенства на матрицу обратную,получим … ля получения системы при m=n в общем виде предположи,что квадратн.матрица системы An*m невырожденная,т.е.её определитьель |A|=0.В этом случае существ.обратная матрица. Умножая слева обе части матричного равенства на матрицу обратную,получим …Т 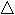 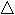 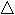 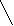   еорема Крамера.Пусть -определитель матрицы системы А,а j-определитель матрицы,получаемый из матрицы А заменой j-го столбца столбцом свободных членов. Тогда,если =0 ,то система имеет единственное решение,определяемое по формулам:Xj= j / , (j=1,2…n) еорема Крамера.Пусть -определитель матрицы системы А,а j-определитель матрицы,получаемый из матрицы А заменой j-го столбца столбцом свободных членов. Тогда,если =0 ,то система имеет единственное решение,определяемое по формулам:Xj= j / , (j=1,2…n)Метод Гаусса.-метод последовательных исключений переменных-с помощью элементарных преобразований система ур-ий приводится к равносильной системе. Ступенчатого(ии тр-го вида) После отбрасывания «лишних»ур-ий возможны два случая:а)число ур-ий системы равно числу переменных т.е.r=n(тр-ый вид)б)r | | ||||
| 13.Решение однородных СЛАУ.Критерий существования ненулевого решения. Фундаментальная система. Система m линейных ур-ий с n переменными назыв.системой линейных однородных ур-ий,если все их свободные члены равны нулю.Имеет вид: 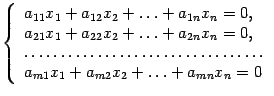 Всегда является совместной.Решение однородн.СЛАУ обладают следующ.св-ами: 1.Если строка l1=(k1,k2,...kn)-решение системы,то и строка …. -также решение этой системы.2.Если строка l1=(k1,k2,...kn) и l2=(l1,l2,...ln)-решения системы,то при любых c1 и c2 их линейная комб-ия c1,l1+c2,l2=(c1k1+c2l1,c1k2+c2l2+...c1kn+c2ln) также решение данной системы. | Критерийненулевого решения однор.СЛАУ: Система линейных однородных уравнений имеет ненулевые решения тогда и только тогда,когда ранг её матрицы коэффициентов при переменных меньше числа переменных,т.е. при r(A) Система линейно независимых решений l1,l2,...lk назыв.фундаментальной,если каждое решение системы является линейной комбинацией решений l1,l2,...lk. Если ранг r матрицы коэффициентов при переменных системы линейных однородных ур-ий меньше числа переменных n,то всякая фундаментальная система решений системы состоит из n-r решений. Поэтому общее решение системы линейных однородных ур-ий имет вид: c1,l1+c2,l2…+сklk,где l1,l2,...lk-любая фундаментальная система решений, с1,с2…сk-произвольные числа и k=n-r. | | ||||
| 14.Декартова прямоуг.система координат.Линейные операции над векторами.Вычисление длины вектора. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат. 1-я OX – ось абсцисс 2-я OY – ось ординат 3-я OZ – ось аппликат. Базис-множество векторов в линейном пространстве, таких, что любой вектор пространства может быть представлен в виде некоторой их конечной линейной комбинации (полнота базиса), при этом ни один из базисных векторов не представим в виде конечной линейной комбинации остальных (линейная независимость). Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат. 1.Проекция суммы векторов на какую-нибудь ось равна сумме их проекции на эту же ось… | 2.При умножении вектора на число проекция умножается на это же число… Векторы назыв.коллинеарными,если лежат на | | прямых или на одной прямой.Признаком коллинеарности 2-х векторов является пропорциональность их координат. Х1 =Y1 =Z1 Х    2 Y2 Z2 2 Y2 Z2Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала. Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то | | ||||
| 14.Декартова прямоуг.система координат.Линейные операции над векторами.Вычисление длины вектора. Если точка М(х, у, z) делит отрезок АВ в соотношении /, то координаты этой точки определяются как: В частном случае координаты середины отрезка находятся как: x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2. Приложение.Пример. Даны векторы | 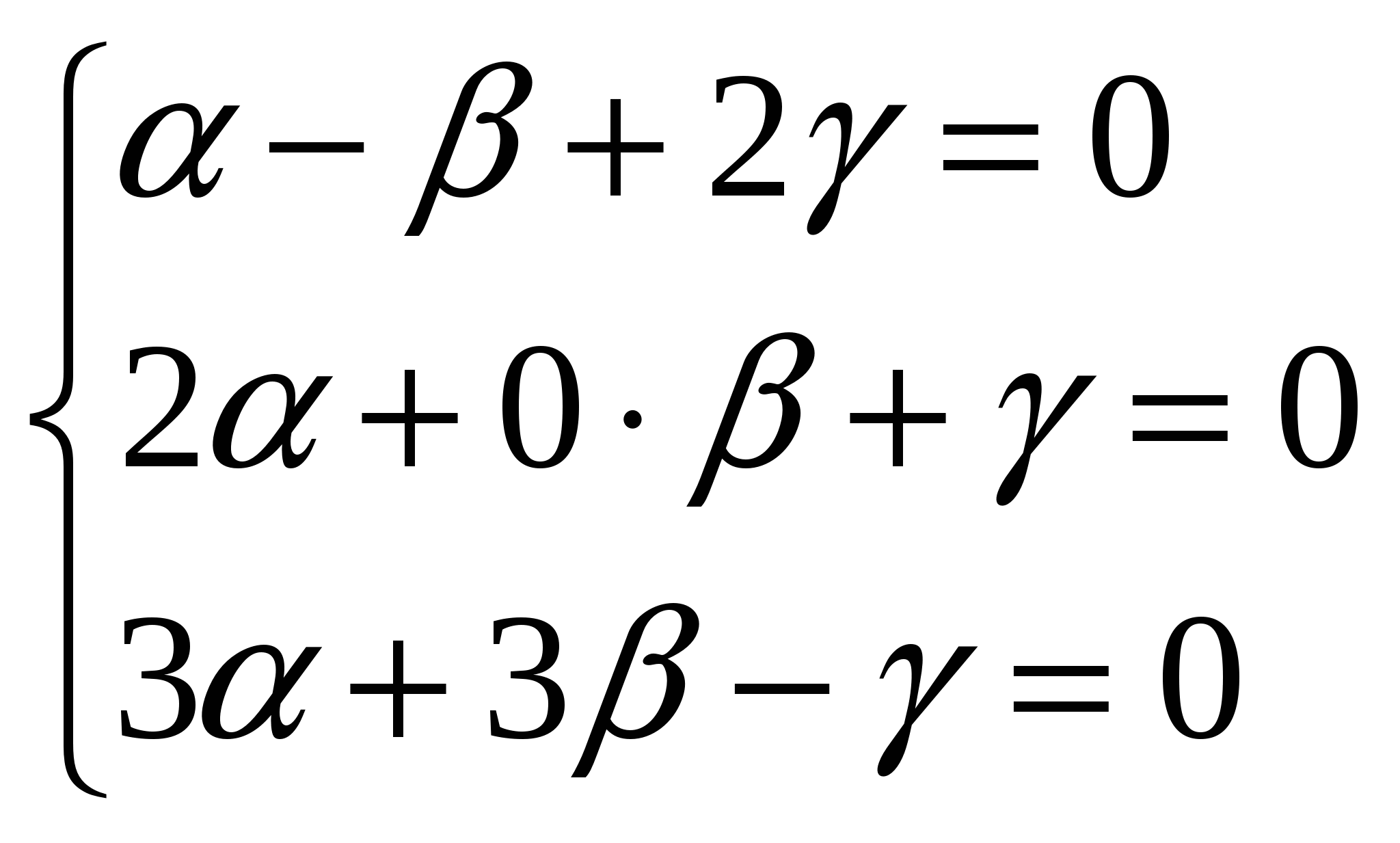 линейно независимы. линейно независимы.Тогда 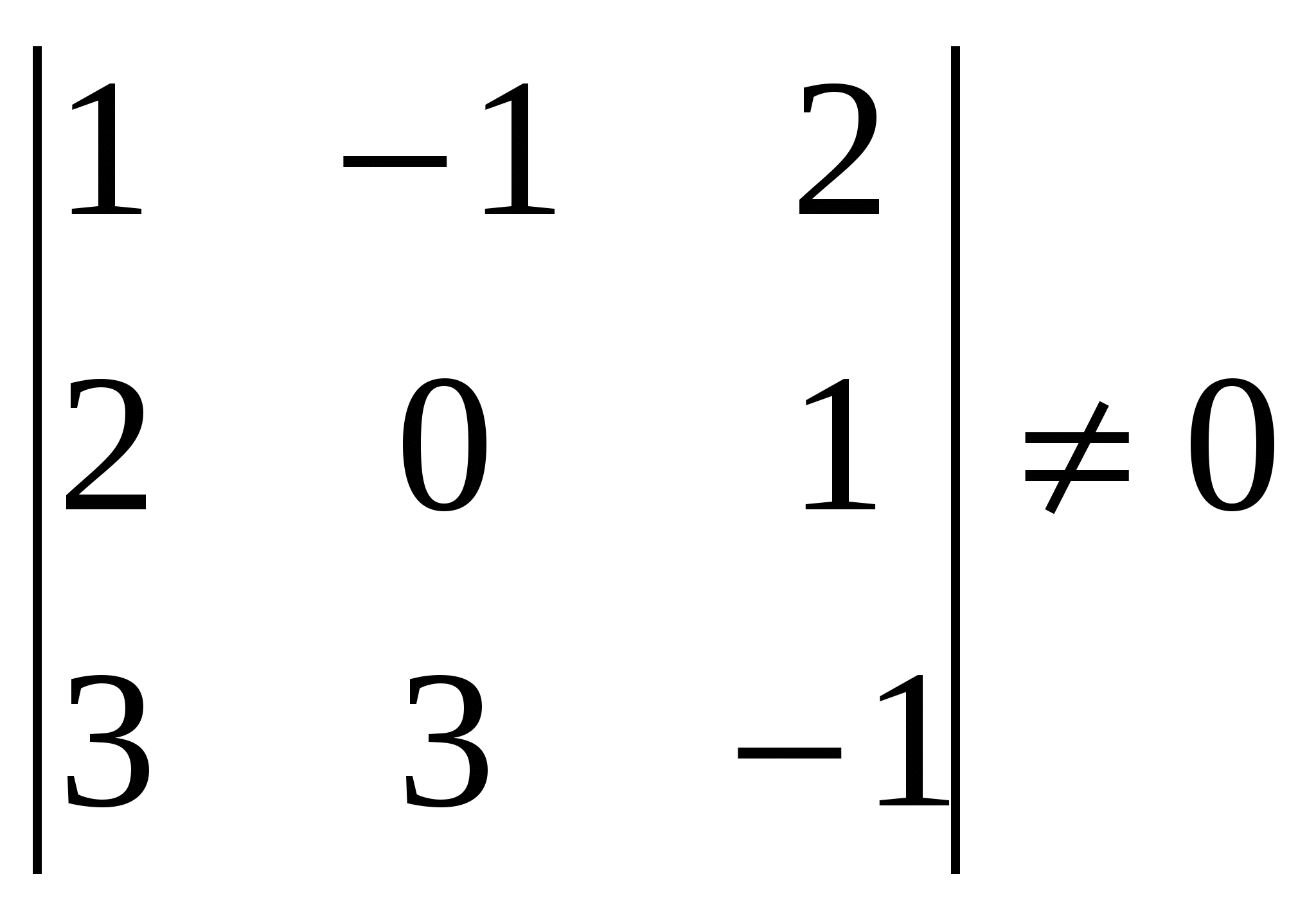   =4 =0 =4 =0 Для решения этой системы воспользуемся методом Крамера. Для решения этой системы воспользуемся методом Крамера. Итого, координаты вектора | | ||||
| 22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. Определения,вывод их канонических ур-ий.Фокусы,эксцентриситет,директр. Кривая второго порядка может быть задана уравнением Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0. Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.    - уравнение эллипса. - уравнение эллипса. a2x2 – c2y2 = 0 – уравнение двух пересекающихся прямых. y2 = 2px – уравнение параболы. y2 – a2 = 0 – уравнение двух параллельных прямых | y2 + a2 = 0 – уравнение двух “мнимых” параллельных прямых. y2 = 0 – пара совпадающих прямых. (x – a)2 + (y – b)2 = R2 – уравнение окружности. Эллипсом назыв.геометрическое место точек,для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина,большая,чем рассточние между фокусами. Гиперболой назыв. геометрическое место точек,для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина.Параболой назыв.геометрическое место точек,для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом,равно расстоянию до некоторой фиксированной прямой,называемой директрисой. | | ||||
| 2  2.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. 2.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. Эллипс. F1, F2 – фокусы. F1 = (c; 0); F2(-c; 0) с – половина расстояния между фокусами; a – большая полуось,называемая эксцентриситетом эллип b – малая полуось.Фокусное расстояние и полуоси эллипса связаны соотношением:a2 = b2 + c2. В случае, если точка М находится на пересечении эллипса с вертикальной осью, r1 + r2 = 2 | r1 + r2 = 2a. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом. Е = с/a. Т.к. с < a, то е < 1. Величина k = b/a называется коэффициентом сжатия эллипса, а величина 1 – k = (a – b)/a называется сжатием эллипса. Коэффициент сжатия и эксцентриситет связаны соотношением: k2 = 1 – e2. Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.Если для точки М(х1, у1) выполняется условие: | | ||||
| 22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. r1 = a – ex, r2 = a + ex Выше было показано, что r1 + r2 = 2a. Кроме того, из геометрических соображений можно записать: 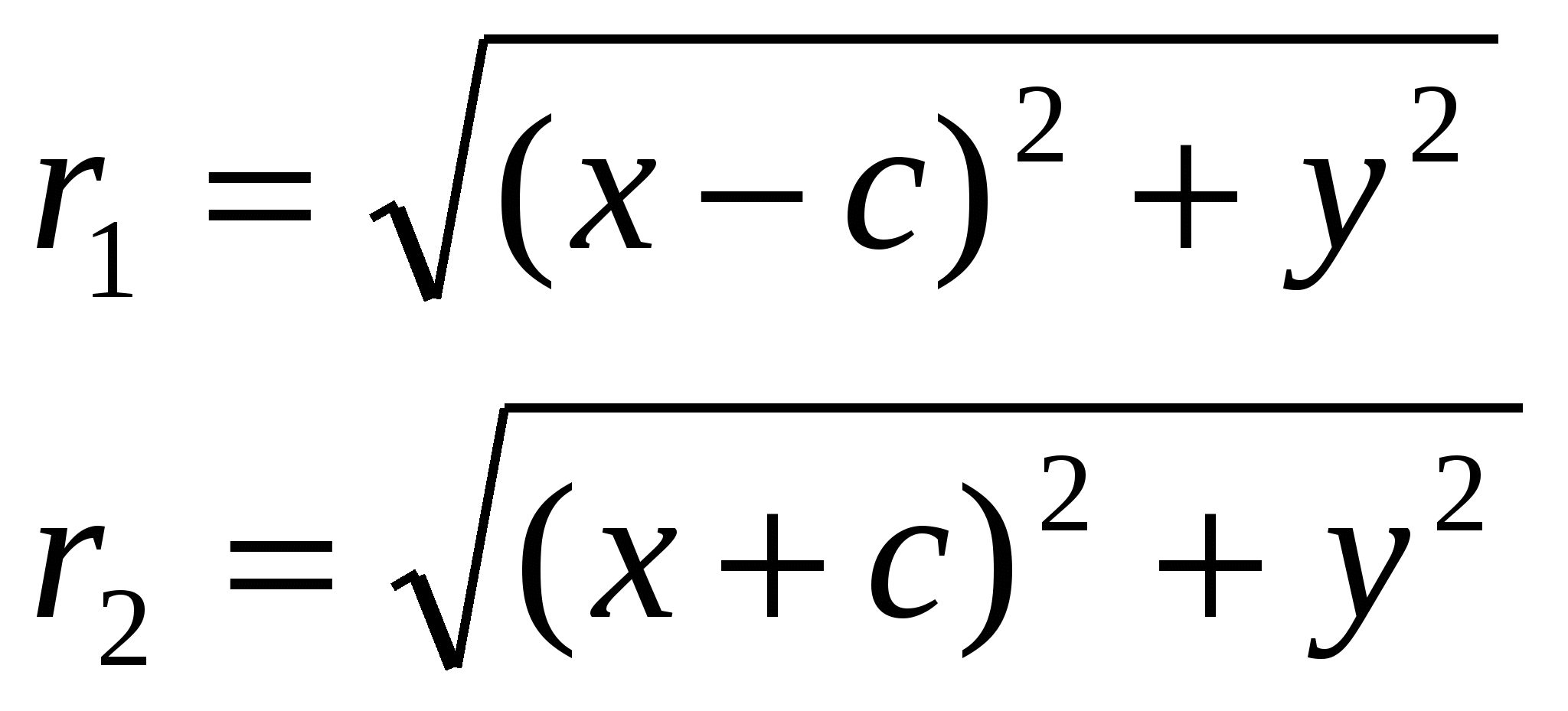 После возведения в квадрат и приведения подобных слагаемых: Аналогично доказывается, что r2 = a + ex. Эллипс определен ур-ем и a>b,то прямые x = a/e; x = -a/e называются директрисами эл. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина. | Г  ипербола. По опреде- ипербола. По опреде-лениюr1 – r2=2a. F1, F2 – фокусы гиперболы. F1F2=2c.Выберем на гиперболе произвольную точку М(х, у). Тогда: 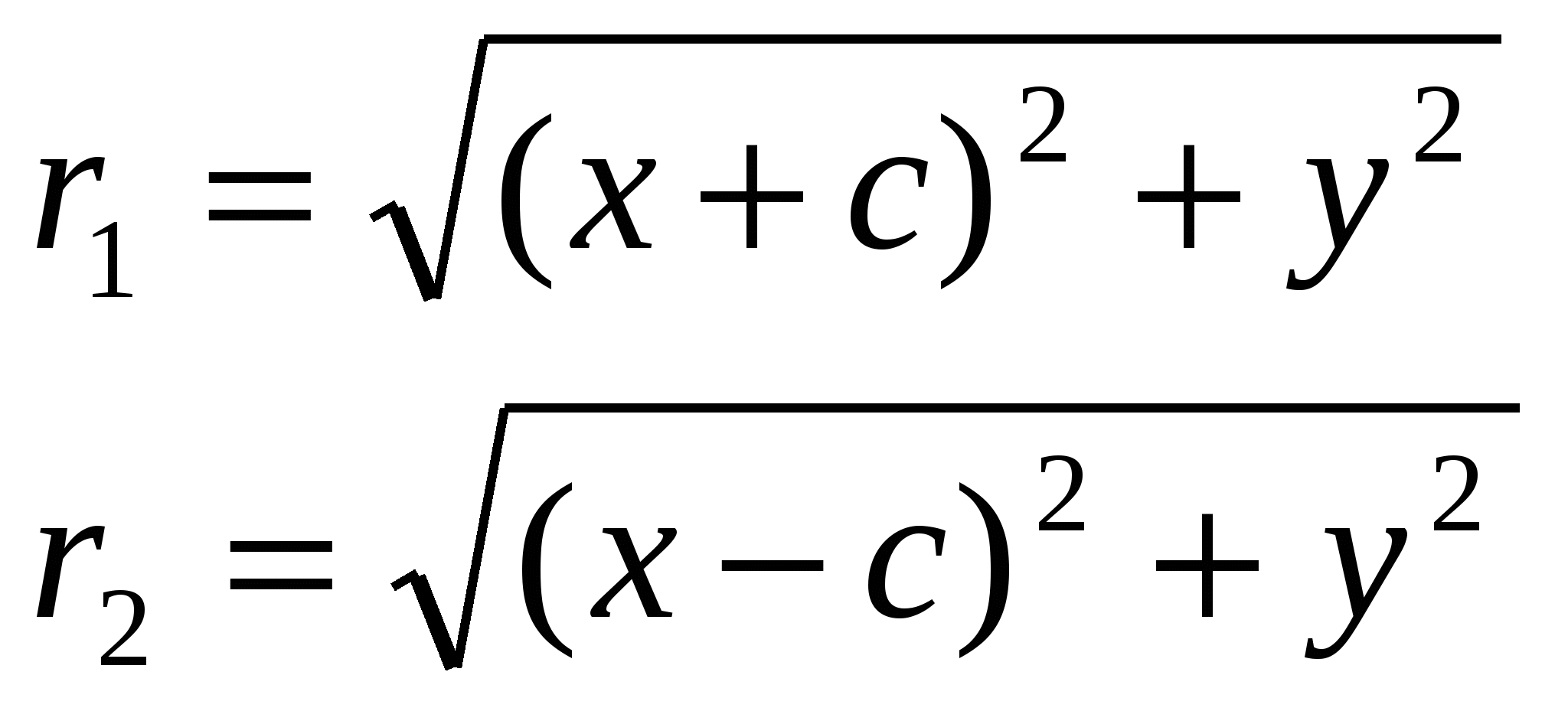 | | ||||
| 22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось) Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Ось 2а называется действительной осью гиперболы. О  сь 2b называется мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых сь 2b называется мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которыхАсимптота кривой γ, имеющей бесконечную ветвь — прямая, обладающая тем свойством, что расстояние от точки γ кривой до этой прямой стремится к нулю при движении её вдоль ветви к бесконечности. | О  тношение тношение | | ||||
