Поручиков М.А. Анализ данных. А. поручиков

• Название: А. поручиков
• Дата: 25.10.2022
• Размер: 2.76 Mb.
• Имя файла: Поручиков М.А. Анализ данных.docx
• Тип: Анализ; #753011
• страница: 7 из 20

РЕГРЕССИОННЫЙ АНАЛИЗ

Общие сведения

Предположим, что есть задача определения стоимости некоторой квартиры. Очевидно, что в общем случае стоимость квартир зависит от многих факторов: площади, географического расположения, этажа и т.п. Зная характер этой зависимости, можно оценить (предсказать) стоимость любой квартиры.

Подобные системы появились на сайтах агентств недвижимости (рис. 7).



Рис. 7. Прогнозирование цены на сайте http://www.irn.ru/price
Предсказание значения зависимой переменной с помощью независимой переменной (независимых переменных) является задачей регрессионного анализа.

Регрессия относится к типу задач обучения с учителем (Supervised Learning в терминах Machine Learning). Предполагается, что имеется некоторая выборка данных, в которой представлены несколько объектов с известными свойствами.

Решение задачи предсказания включает два этапа: поиск характера зависимости и собственно предсказание (рис. 8).овые объекты

Параметры новых объектов

Набор объектов с известными параметрами
Параметры регрес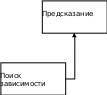сии

Рис. 8. Схема применения регрессии
Наиболее часто используется линейная функция гипотезы



m

^{h(x)  }₀ ^{ x0  }₁ ^{ x1  }_m^{ xm} _^ _j^{ xj}. (1)

j0

С учетом того, что наборы значений  и x по сути являются векторами, выражение (1) для удобства записывают в виде произведения векторов:

h(x)  x ^{. (2)}

В зависимости от характера функции гипотезы регрессию подразделяют на линейную и нелинейную. В зависимости от числа независимых переменных регрессию подразделяют на парную и множественную.

Примером парной линейной регрессии является задача выявления зависимости стоимости квартир от их площади (табл. 9, рис. 9).
Таблица 9. Характеристики квартир

Площадь, кв. м	Стоимость, млн. руб.
34	1,3
40	2,9
59	3,0
85	6,5

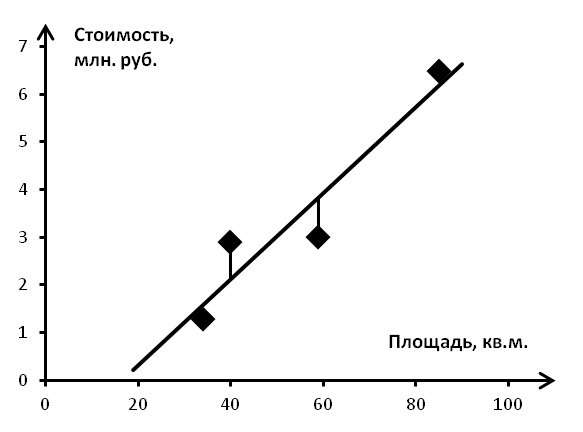Рис. 9. Регрессия с помощью линейной функции
Подбор параметров регрессионной функции обычно осуществляется по критерию минимума суммы квадратов отклонений:

CF

h(x)  y²  min ^{. (3)}

n
 ⁱⁱi1

ii
^{При этом выражение} h(x)  y²

называется функцией штрафа

(cost function, CF; либо loss function, LF).

В формулировке (3) задача нахождения параметров регрессионной функции является оптимизационной. Существует два основных подхода к решению задачи регрессии в постановке (1): аналитический и численный. Следует отметить, что решения регрессионной задачи, полученные разными методами, могут различаться.