Поручиков М.А. Анализ данных. А. поручиков
 Скачать 2.76 Mb.
|
Выбор функции гипотезы 1,5062 0,0905 70 4,83 млн. руб. Одной из важных задач регрессионного анализа является задача выбора функции гипотезы. В случае парной регрессии выбор функции гипотезы можно осуществлять визуально по соответствующему графику. В случае множественной регрессии этот подход неприменим. Предположим, что имеются данные о стоимости квартир (табл. 10). Таблица 10. Стоимость квартир
Рассмотрим два варианта решения задачи регрессии с применением линейной функции гипотезы и функции гипотезы, представляющей собой полином четвёртой степени. Опуская подробности решения этой задачи, приведем результаты (табл. 11, рис. 15). Таблица 11. Параметры решений для различных функций гипотезы
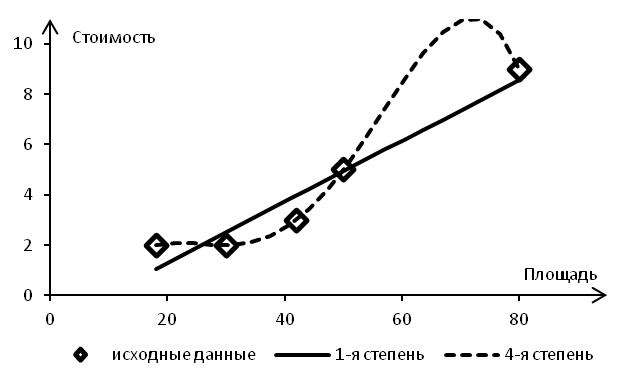 Рис. 15. Регрессия при разных функциях гипотезы С точки зрения минимизации функции штрафа из представленных функций следует выбрать полином четвертой степени. С другой стороны, очевидно, что такая функция уже не вполне адекватно отражает тенденцию роста стоимости квартир с возрастанием их площади. В терминологии Machine Learning ситуация, иллюстрируемая сплошной линией (рис. 15), соответствующей линейной функции гипотезы, обозначается термином underfitting (недообученность). В этом случае общая тенденция уже проявляется, но функция прогноза недостаточно хорошо аппроксимирует имеющийся набор данных. Ситуация, иллюстрируемая пунктирной линией (рис. 15), соответствующей полиномиальной функции регрессии, обозначается термином «переобученность» (overfitting). Эта ситуация может быть описана следующим образом: аппроксимация очень хорошо либо идеально описывает выборку данных, но способность к обобщению потеряна. Существуют разные способы выбора функции регрессии. Один из способов предполагает выполнение следующих шагов: Разделение случайным образом исходной выборки данных на две части: обучающую, содержащую от 70 до 80% исходных данных, и проверочную, содержащую от 20 до 30% исходных данных. Задание нескольких функций гипотезы. Выполнение для каждой из функций гипотезы подбора параметров функции по обучающей выборке (минимизация функции штрафа по обучающей выборке) и вычисления функции штрафа по тестовой выборке. Выбор функции гипотезы по критерию минимальной функции штрафа по тестовой выборке. Рассмотрим пример выбора функции гипотезы на примере данных о площади и стоимости квартир (табл. 12, рис. 16). Таблица 12. Стоимость квартир
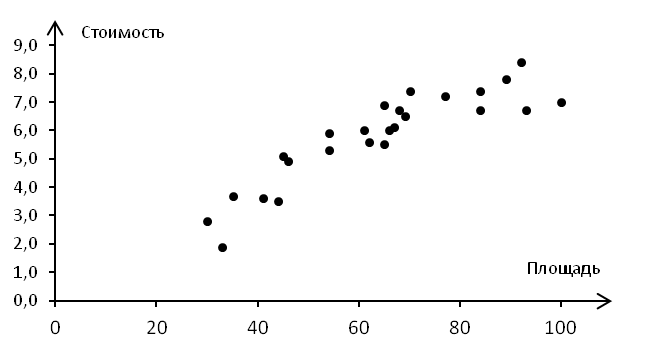 Рис. 16. Исходная выборка данных по стоимости квартир Разделим исходную выборку данных на обучающую, содержащую 20 (80%) записей из исходной выборки (табл. 13), и проверочную, содержащую 5 (20%) записей из сходной выборки (табл. 14). Таблица 13. Обучающая выборка
Таблица 14. Проверочная выборка
Графическая интерпретация разделения исходной выборки на две приведена ниже (рис. 17). 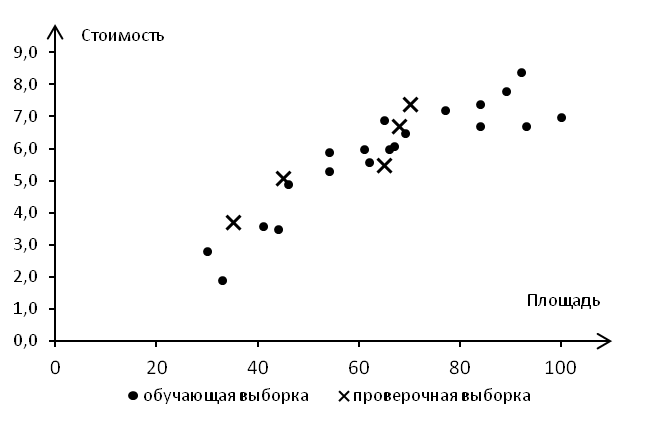 Рис. 17. Обучающая и проверочная выборки Решение задачи регрессии приводит к следующим показателям (рис. 18). Таким образом, исходя из критерия минимума функции штрафа по проверочной выборке, можно сделать вывод о том, что наиболее подходящей в данном случае является квадратичная функция гипотезы. 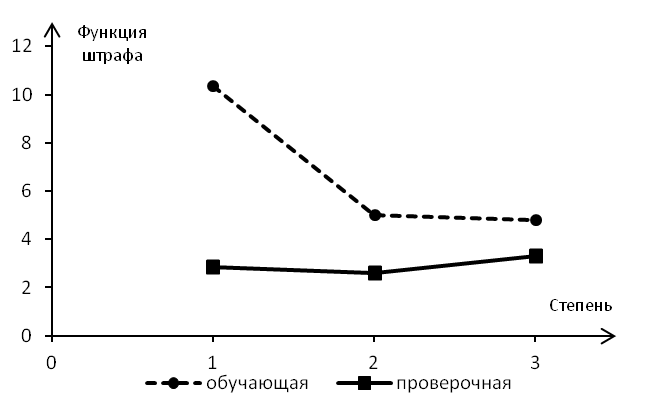 Рис. 18. Зависимость ошибки от степени функции регрессии |