Поручиков М.А. Анализ данных. А. поручиков

• Название: А. поручиков
• Дата: 25.10.2022
• Размер: 2.76 Mb.
• Имя файла: Поручиков М.А. Анализ данных.docx
• Тип: Анализ; #753011
• страница: 8 из 20

Аналитическое решение

Известно аналитическое решение задачи линейной регрессии в постановке (1):

  ( X^TX)^1 X^Ty, (4)

где X– матрица, содержащая значения независимых переменных,

y– вектор, содержащий значений зависимых переменных.

Для вышеприведенного набора данных (табл. 9) матрица Х

и вектор yпримут вид

^{1 34}

^1 40^

^1,3 

^2,9^

^{X  } , y ^{ } . (5)

^1 59^{ }3,0^

   

_1 85_{ }6,5_

При исходных данных (3) выражение (2) дает результат


 
_{ } ^{ 1,506} _.

0,090

 

Для вычисления выражений вида (2) удобно использовать специализированное математическое программное обеспечение, например Matlab, Octave. Однако широко распространенное ПО Microsoft Excel также имеет инструменты для решения подобных задач. Так, для умножения матриц используется функция МУМНОЖ, для транспонирования матриц – функция ТРАНСП, а для нахождения обратной матрицы – МОБР (рис. 10, рис. 11).





Рис. 10. Вычисления в Microsoft Excel (режим значений)

Рис. 11. Вычисления в Microsoft Excel (режим формул)
Данный метод характеризуется следующими особенностями:

1. 
   Относительно низкая устойчивость к отдельным сочетаниям данных. Так, дублирование какой-либо строки в наборе данных приведет к сбою в вычислениях при операции нахождения обратной матрицы.
   
2. 
   Большая вычислительная сложность. Относительно большие наборы данных, содержащие порядка тысячи и более строк, будут обрабатываться относительно медленно.
   
3. 
   Чувствительность к большим значениям. Для наборов данных, в отдельных столбцах которых содержатся большие значения, может потребоваться предварительная нормализация.
   

Численное решение

Для линейной регрессии задача в формулировке (1) имеет единственное решение, что позволяет без каких-либо оговорок применять численные методы. Например, можно использовать метод Ньютона либо метод сопряженных градиентов. Оба этих метода представлены в инструменте «Поиск решения» ПО Microsoft Excel.

Численное решение регрессионной задачи включает следующие шаги:

1. 
   подготовку данных;
   
2. 
   задание функции гипотезы, в том числе начальных значений её параметров;
   
3. 
   задание целевой функции;
   
4. 
   решение оптимизационной задачи каким-либо численным методом.
   

Рассмотрим численное решение задачи регрессии на основе данных о стоимости квартир (табл. 9) с помощью программного обеспечения Microsoft Excel.

Для удобства запишем выражение для функции гипотезы в следующей форме:

h(x)  a₀  a₁  x ^{. (6)}

Также запишем формулировку оптимизационной задачи:

CF

(a a x)  y²  min ^{. (7)}

4
 ^{0 1 1 i}i1

Зададим функцию гипотезы и начальные значения коэффициентов функции гипотезы, зададим функцию штрафа (рис. 12).



Рис. 12. Подготовка к численному решению
В настройках инструмента «Поиск решения» зададим целевую ячейку, содержащую выражение для функции штрафа, и изменяемые ячейки, содержащие значения коэффициентов функции гипотезы (рис. 13).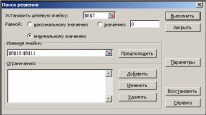

Рис. 13. Параметры поиска решения
В результате решения задачи (7) с помощью инструмента «Поиск решения» получим значения коэффициентов функции гипотезы a₀  1,5062 , a₁  0,0905 .

График функции гипотезы представляет собой прямую линию (рис. 14).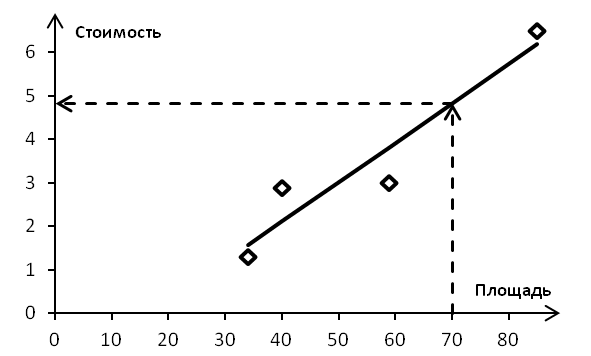




Рис. 14. Прогноз по графику функции гипотезы
Прогнозирование стоимости квартиры осуществляется с помощью подстановки площади квартиры и найденных коэффициентов

в выражение (6). Например, для квартиры площадью 70 кв. м

прогнозная стоимость составит (рис. 14).