сборник. Сборник творческойгруппы. Администрация департамент образования
 Скачать 3.12 Mb. Скачать 3.12 Mb.
|
Существуют различные типы уравнений, содержащих параметры:I тип. Уравнения, которые необходимо решить для всех возможных значений параметра.II тип. Уравнения, для которых необходимо определить количество решений в зависимости от значения параметра.III тип. Уравнения, для которых требуется найти все те значения параметра, при которых указанное уравнение имеет заданное число решений (в частности, не имеют или имеют бесконечное множество решений). Последние два типа задач отличает то, что при их решении не требуется получить явное решение, а нужно лишь найти те значения параметра, при которых это решение удовлетворяет тем или иным условиям. Примерами таких условий могут служить следующие:существуют решения; не существуют решения; существует единственное решение; существует положительное решение: существует ровно kрешений; существует решение, принадлежащее указанному промежутку. Именно в этих случаях оказывается очень полезным графический способ решения уравнений с параметрами. Алгоритм решения уравнения с параметром графическим способом. Находим область допустимых значений уравнения. Выражаем параметр, как функцию от переменной 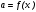 . .Производим замену 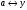 . .В прямоугольной системе координат хОу строим график функции 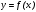 для тех значений х, которые входят в область допустимых значений данного уравнения. для тех значений х, которые входят в область допустимых значений данного уравнения.Рассматриваем семейство прямых 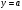 . .Находим точки пересечения прямой 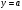 с графиком функции с графиком функции 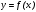 . Если прямая . Если прямая 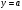 пересекает график пересекает график 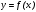 , то определяем абсциссы точек пересечения, решая уравнение , то определяем абсциссы точек пересечения, решая уравнение 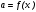 относительно х. При необходимости находим ординаты этих точек. относительно х. При необходимости находим ординаты этих точек.Отвечаем на поставленный вопрос задания. Пример 1. При каких значениях параметра а уравнение 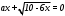 имеет решения на отрезке имеет решения на отрезке 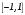 ? ?Решение. 1). ОДЗ: 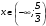 . . 2). Выражаем параметр 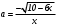 . . 3). Делаем замену 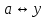 . . 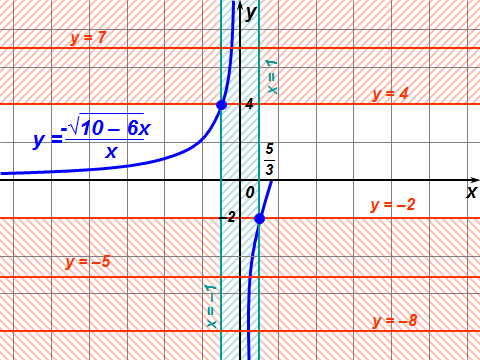 4). Строим график функции 4). Строим график функции 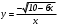 , где , где 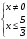 . .5). Если 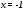 , то , то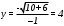 ; если ; если 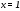 , то , то 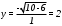 . .На рисунке видим, что при 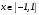 прямые прямые 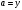 будут пересекать график только если будут пересекать график только если 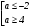 Ответ: 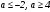 . .Пример 2. Найдите число решений уравнения 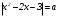 в зависимости от параметра а. в зависимости от параметра а.Решение. 1). ОДЗ: 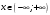 . .2). Делаем замену 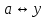 . . 3). Построим график функции 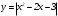 . .Выделим полный квадрат 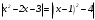 Уравнение 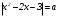 имеет столько решений, сколько раз прямая имеет столько решений, сколько раз прямая 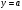 пересекает график функции пересекает график функции 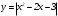 . .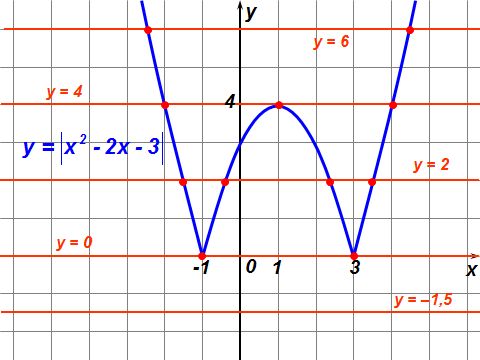 На рисунке видно: 1) если 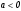 , то графики не имеют общих точек, т.е. нет решения; , то графики не имеют общих точек, т.е. нет решения;2) если 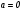 , то графики имеют две общие точки, т.е. два решения; , то графики имеют две общие точки, т.е. два решения;3) если 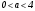 , то графики пересекаются в четырех точках, что дает четыре решения; , то графики пересекаются в четырех точках, что дает четыре решения;4) если 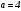 , то графики имеют три общие точки, т.е. три решения; , то графики имеют три общие точки, т.е. три решения;5) если 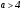 , то графики имеют две общие точки, т.е. два решения. , то графики имеют две общие точки, т.е. два решения.Ответ: при 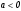 нет решений; при нет решений; при 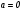 и и 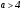 два решения; два решения; при 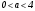 четыре решения; при четыре решения; при 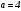 три решения. три решения.Пример 3. При каких значениях параметра а уравнение 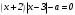 имеет три действительных корня? имеет три действительных корня?Решение. 1). ОДЗ: 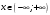 . . 2). Выражаем параметр 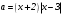 . . 3). Делаем замену 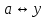 . . 4). Строим график функции 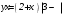 . .Преобразуем функцию к виду: 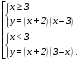 Из рисунка видно, что система имеет три решения, если 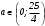 , где , где 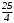 – ордината вершины параболы, значение которой нетрудно определить. – ордината вершины параболы, значение которой нетрудно определить.Ответ: 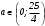 . .Пример 4.При каких значениях параметра а уравнения 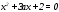 и и 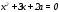 имеют хотя бы один общий действительный корень? имеют хотя бы один общий действительный корень?Решение. 1). ОДЗ: 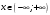 . .2). Выражаем параметр в обоих уравнениях 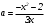 и и 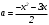 . . 3). Делаем замену 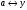 . . 4). Построим графики функций 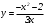 и и 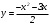 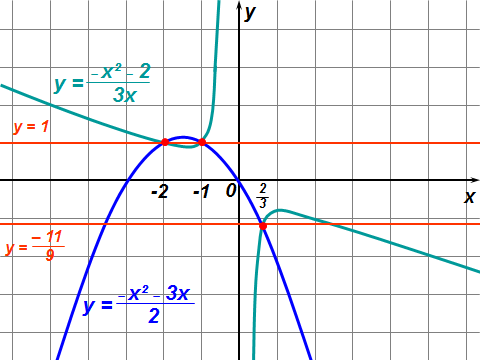 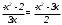 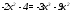 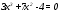 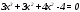 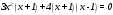 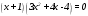 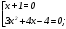 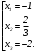 Находим координаты искомых точек: 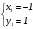 или или 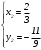 или или 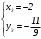 Ответ: 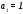 ; ;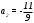 . .Пример 5. При каких значениях параметра 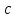 уравнение уравнение 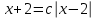 имеет единственное решение? имеет единственное решение?Решение. 1). ОДЗ: 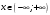 . .2).Выражаем параметр 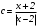 . . 3). Делаем замену 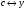 . . 4). Построим график функции 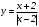 . .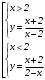 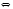 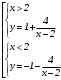 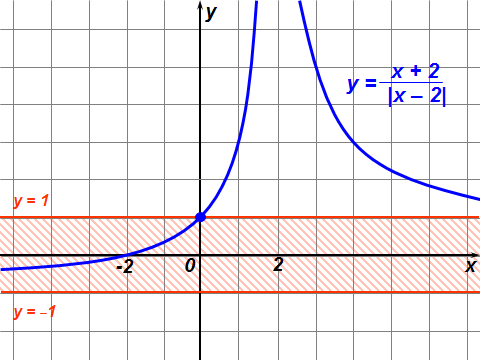 Из рисунка видим, что уравнение имеет одно решение при 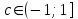 . .Ответ: 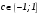 . .Литература: Алгебра. 10-11 класс. В 2 ч. /[А.Г.Мордкович и др.] под ред. А.Г. Мордковича. – 11-е изд. Стер. М.: Мнемозина, 2009. Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. – 9-е изд.- М.: Айрис-пресс, 2004 – 432с. Субханкулова С.А. Задачи с параметрами. – М.: ИЛЕКСА, 2010. – 208с (Серия «Математика: элективный курс»). Ушакова И.А. Учитель математики МБОУ СОШ №3 «Математика владеет не только истиной, но и высшей красотой» Бертран Рассел. Аналитический и графический способы решения линейных уравнений. Пример 1.Решите уравнение 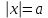 . .Решение: Способ 1. (аналитический). При а>0уравнение имеет два корня: 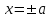 . .При а=0 уравнение имеет один корень: х=0 При а<0уравнение корней не имеет. СпособII.(графический) 1 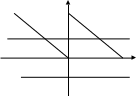 . При а>0 графики пересекаются в двух точках (– а; а) и (а; а), значит уравнение имеет два решение: . При а>0 графики пересекаются в двух точках (– а; а) и (а; а), значит уравнение имеет два решение: 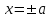 . .У 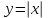 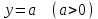 х х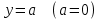 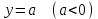 2. При а=0 точка пересечения графиков одна – начало координат, следовательно, уравнение имеет одно решение: х=0. При а<0графики функции не пересекаются – решений нет. Ответ: при а<0 корней нет; при а=0 один корень: х=0; при а>0 два корня: 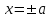 . .Пример 2.Решите уравнение 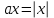 . .Решение. Способ I (аналитический). 1. При 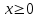 уравнение равносильно уравнению ах = х, или х(а — 1) = 0. Следовательно: уравнение равносильно уравнению ах = х, или х(а — 1) = 0. Следовательно:а) при а ≠ 1 уравнение имеет только одно решение: х = 0; б) при а = 1 уравнение имеет бесконечное множество решений: 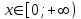 2. При х ≤ 0 уравнение равносильно уравнению ах = —х, или х(а + 1) = 0. Следовательно: а) при а ≠ —1 уравнение имеет одно решение: х = 0; б) при а = —1 - множество решений, 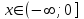 Способ II (графический). П 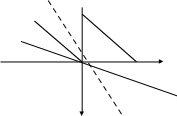 остроим графики функций остроим графики функций 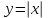 и и 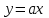 . Графиками функций у = ах являются прямые, проходящие через начало координат, угловой коэффициент которых равен а. . Графиками функций у = ах являются прямые, проходящие через начало координат, угловой коэффициент которых равен а.у А В 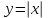 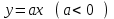 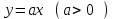 1. При 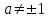 уравнение имеет одно решение х = 0. уравнение имеет одно решение х = 0.2. При а = 1 прямая у = х содержит луч ОА, и уравнение имеет бесконечное множество решений 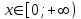 . .З. При а = —1прямаяу =х содержит луч ОВ, и уравнение имеет бесконечное множество решений 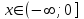 Ответ :при а = —1 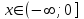 ; при а = 1 ; при а = 1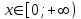 ;при ;при 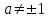 х = 0. х = 0.Пример 3. Решите уравнение | х + 2| = ах + 1. Решение аналитическим способом приводит к достаточно длительным рассуждениям, так как имеет много ветвлений. Графический способ более удобен, он короче и красивее. Решение. Построим график функций у =| х + 2| и у = ах + 1. График первой функции получается сдвигом графика функции у =| х| на 2 единицы влево по оси абсцисс. Графиком второй функции является прямая, проходящая через точку с координатами (0; 1), угловой коэффициент которой равен а. Рассматривая график функции у = ах + 1 при различных числовых значениях параметра а, получаем пучок прямых, проходящих через точку (0; 1). 1 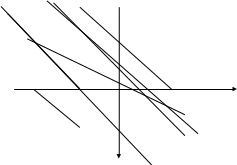 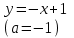 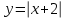 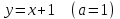 3 2  2 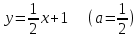 1 -2 -1 1 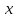 3 Если угловой коэффициент 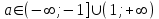 , то есть прямые проходят в области 1, то они пересекает правую ветвь (х> –2) графика функции , то есть прямые проходят в области 1, то они пересекает правую ветвь (х> –2) графика функции 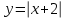 , и уравнение имеет одно решение. , и уравнение имеет одно решение.Если 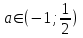 , то прямые проходят в области 2, и графики функций пересекаются в двух точках, то есть уравнение имеет два решения. , то прямые проходят в области 2, и графики функций пересекаются в двух точках, то есть уравнение имеет два решения.При 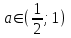 прямые расположены в области 3, в этом случае графики функций не пересекаются, следовательно, уравнение решений не имеет. прямые расположены в области 3, в этом случае графики функций не пересекаются, следовательно, уравнение решений не имеет.При 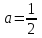 точка пересечения одна, и решение тоже одно. точка пересечения одна, и решение тоже одно.Таким образом, получаем ответ. Ответ: при 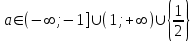 уравнение имеет одно решение; при уравнение имеет одно решение; при 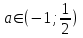 уравнение имеет два решения; при уравнение имеет два решения; при 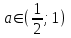 уравнение решений не имеет. уравнение решений не имеет.Литература: Виленкин Н.Я., Сурвилло Г.С., Симонов А.С., Кудрявцев А.И. Алгебра для 9 класса: Учеб.пособие для учащихся шк. и классов с углубл. изуч. математики. – М.: Просвещение, 2001. – 384 с. Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. 3-е издание, дополненное и переработанное. – М.: Илекса, Харьков: Гимназия, 1998, – 336с. Соколовская Т.Н. Директор МБОУ СОШ №3 «Для того чтобы усовершенствовать ум, надо больше рассуждать, чем заучивать». Р.Декарт |
