сборник. Сборник творческойгруппы. Администрация департамент образования
 Скачать 3.12 Mb. Скачать 3.12 Mb.
|
|
1. 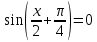 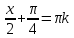 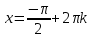 2. 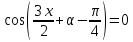 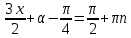 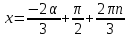 Нам надо, чтобы было нечетное число корней. Первое уравнение одно решение 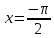 . Второе давать 3 решения на периоде (это становится понятным, если посмотреть на слагаемое . Второе давать 3 решения на периоде (это становится понятным, если посмотреть на слагаемое 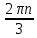 ) )Таким образом, нечетное число корней (а точнее – 3 корня) будет если одно из решений второго уравнения совпадает с 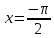 или попадает в точку π, т.е. не входит в рассматриваемый промежуток. или попадает в точку π, т.е. не входит в рассматриваемый промежуток. Рассмотрим эти случаи. 1. 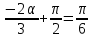 ; ; 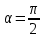 Тогда: 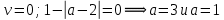 Но при а=1 u=0, а это невозможно. 2.  ; ; 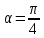 Тогда: 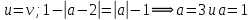 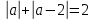 а) 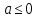 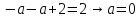 б) 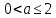 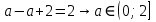 в) 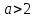 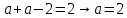 Т.о. 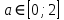 Ответ: 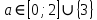 Пример 14. Найти все значения параметра а, при которых система имеет хотя бы одно решение. Найдите эти решения. Решение. Преобразуем первое уравнение: 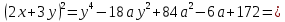 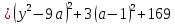 Наименьшее значение выражения, стоящего в правой части равно 169. Оценим левую часть, воспользуемся неравенством Коши-Буняковского: Тогда: 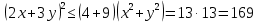 Найдем при каких а, х, у правая и левая часть достигают своих наибольшего и наименьшего значения соответственно: 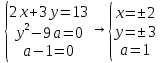 Ответ: 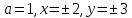 Пример 15. При каких значениях а уравнение Решение. Воспользуемся формулой понижения степени cos: cos2α = (1 + cos 2α) / 2 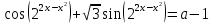 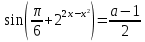 Выполним оценку. Так как 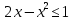 (парабола ветви вниз, вершина хв=1), то (парабола ветви вниз, вершина хв=1), то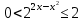 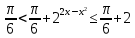 Значит: 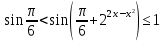 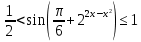 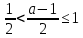 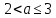 Ответ: 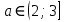 Литература. Высоцкий В. С. Задачи с параметрами при подготовке к ЕГЭ. – М.: Научный мир, 2011. – 316 с. П.И.Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. «Гимназия». Москва-Харьков. 2003 г. Задачи с параметрами.- Координатно-параметрический метод.- Учебное пособие /В.П. Моденов. - М.:Издательство "Экзамен", 2006. Зарецкая И.Ф. учитель математики МБОУ СОШ мкр. Вынгапуровский Методические рекомендации при изучении тем. Линейные и квадратные уравнения Линейное уравнение, записанное в общем виде, можно рассматривать как уравнение с параметрами: ах = b, где х – неизвестное, а, b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном. При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него. Особым значением параметра а является значение а = 0. 1. Если а ≠ 0 , то при любой паре параметров а и b оно имеет единственное решение х = 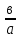 . .2. Если а = 0, то уравнение принимает вид: 0 х = b. В этом случае значение b = 0 является особым значением параметра b. 2.1. При b ≠ 0 уравнение решений не имеет. 2.2. При b = 0 уравнение примет вид: 0 х = 0. Решением данного уравнения является любое действительное число. Пример1. Решить уравнение 2а(а — 2) х = а — 2. (1) Решение. Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в 0. Такими значениями являются а=0 и а=2. При этих значениях а невозможно деление обеих частей уравнения на коэффициент при х. В то же время при значениях параметра а≠0, а≠2 это деление возможно. Таким образом, целесообразно множество всех действительных значений параметра разбить на подмножества A1={0}, А2={2} и А3= {а≠0, а≠2} и решить уравнение (1) на каждом из этих подмножеств, т. е. решить уравнение (1) как семейство уравнений, получающихся из него при следующих значениях параметра: 1) а=0 ; 2) а=2 ; 3) а≠0, а≠2. Рассмотрим эти случаи. 1) При а=0уравнение (1) принимает вид 0 х = - 2. Это уравнение не имеет корней. 2) При а=2уравнение (1) принимает вид 0 х=0. Корнем этого уравнения является любое действительное число. 3) При а≠0, а≠2 из уравнения (1) получаем, х = 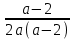 , откуда х = , откуда х = 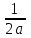 . .0твет: 1) Если а=0,то корней нет; 2) если а=2, то х – любое действительное число; 3) если а≠0, а≠2 , то х = 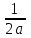 . .Пример2. Решить уравнение (а — 1) х2+2 (2а+1) х+(4а+3) =0; (2) Решение. В данном случае контрольным является значение a=1. Дело в том, что при a=1 уравнение (2) является линейным, а при а≠ 1 оно квадратное (в этом и состоит качественное изменение уравнения). Значит, целесообразно рассмотреть уравнение (2) как семейство уравнений, получающихся из него при следующих значениях параметра: 1) а = l; 2) а≠1. Рассмотрим эти случаи. 1) При a=1 уравнение (2) примет вид 6х+7=0. Из этого уравнения находим х = - 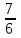 . . 2) Из множества значений параметра а ≠ 1 выделим те значения, при которых дискриминант уравнения (2) обращается в 0. Дело в том, что если дискриминант D=0 при а=ао, то при переходе значения D через точку аодискриминант может изменить знак (например, при а<аоD< 0, а при а>аоD>0). Вместе с этим при переходе через точку ао меняется и число действительных корней квадратного уравнения (в нашем примере при а<аокорней нет, так как D< 0, а при а>аоD>0 уравнение имеет два корня). Значит, можно говорить о качественном изменении уравнения. Поэтому значения параметра, при которых обращается в 0 дискриминант квадратного уравнения, также относят к контрольным значениям. Составим дискриминант уравнения (2): 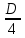 =(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем =(2а+ l)2 — (а — 1) (4а+3). После упрощений получаем 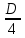 = 5а+4. = 5а+4.Из уравнения 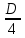 = 0 находим а = - = 0 находим а = -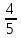 — второе контрольное значение параметра а. При этом если а <- — второе контрольное значение параметра а. При этом если а <-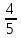 , то D <0; если a≥- , то D <0; если a≥-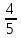 , то D≥0, a ≠ 1.Таким образом, осталось решить уравнение (2) в случае, когда а <- , то D≥0, a ≠ 1.Таким образом, осталось решить уравнение (2) в случае, когда а <-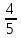 и в случае, когда { a≥- и в случае, когда { a≥-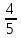 , a ≠ 1 }. Если а <- , a ≠ 1 }. Если а <-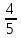 , то уравнение (2) не имеет действительных корней; если же , то уравнение (2) не имеет действительных корней; если же{ a≥- 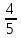 , a ≠ 1 }, то находим , a ≠ 1 }, то находим Ответ: 1) если а <- 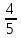 , то корней нет; 2) если а = 1, то х = - , то корней нет; 2) если а = 1, то х = -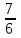 ; ;3) если a≥- 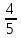 , a ≠ 1, то . , a ≠ 1, то . 2. Свойства квадратичной функции в задачах с параметрами. При решении различных задач часто используются не только свойства квадратного уравнения, но и свойства квадратичной функции. Полезно дать учащимся таблицу, позволяющую составлять систему неравенств для нахождения решений задачи.Однако, на мой взгляд, для рационального подхода к поиску решения достаточно рассмотреть только расположение графиков при положительном старшем коэффициенте, но обратить внимание, что тогда неравенства составляются в виде  аf(A)< 0 или аf(A)> 0 (а- старший коэффициент). аf(A)< 0 или аf(A)> 0 (а- старший коэффициент).Пример1. При каких значениях параметра а один из корней уравнения (а2-2)х2+(а2+а-1)х-а3+а=0 больше числа а, а другой меньше числа а? Решение. Задача равносильна следующей: при каких значениях параметра а нули квадратичной функции g(х)= (а2-2)х2+(а2+а-1)х-а3+а лежат на вещественной оси по разные стороны от точки х = а? Исходя из таблицы, имеем условие: аf(A)< 0. В нашем случае это условие принимает вид (а2-2) g(а)<0. Следовательно, требованию задачи удовлетворяют решения неравенства (а2-2)((а2-2)а2+(а2+а-1)а-а3+а)<0, где а2-2 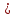 0 (а = 0 (а =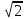 , а =- , а =-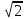 требованию задачи не удовлетворяют). требованию задачи не удовлетворяют). Решая полученное неравенство, находим, что а 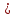 (- (-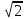 ; -1) ; -1)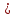 (1; (1; 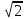 ). ). Ответ: При а 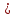 (- (-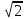 ; -1) ; -1)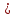 (1; (1; 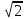 ). ). Пример2. При каких значениях параметра  корни уравнения корни уравнения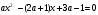 (1) больше 1? (1) больше 1?Решение. Очевидно, что задача равносильна следующей: при каких значениях параметра  корни квадратного трехчлена корни квадратного трехчлена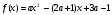 больше 1? Переход от одной формулировки задачи к другой подчеркивает ту общую часто используемую при решении алгебраических уравнений второй степени идею, которая связана с описанием тех или иных свойств квадратного трехчлена и их геометрической интерпретации на графике. В частности, для того, чтобы корни квадратного трехчлена 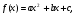 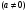 (2) (2)были больше числа 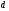 , необходимо и достаточно выполнение условий , необходимо и достаточно выполнение условий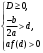 (3) (3)(см. рис. 1.1.) Условия (3) равносильны условиям 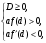 где 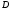 - дискриминант, а - дискриминант, а 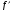 - производная квадратного трехчлена. Требование же того, чтобы корни квадратного трехчлена были меньше числа - производная квадратного трехчлена. Требование же того, чтобы корни квадратного трехчлена были меньше числа 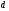 , означает выполнение условий , означает выполнение условий 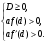 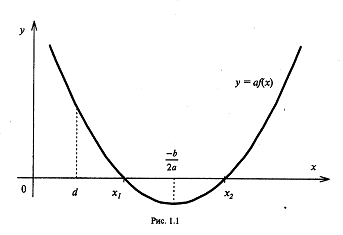 Возвращаясь к исходной задаче, замечаем, что при  =0 уравнение (1) имеет корень =0 уравнение (1) имеет корень 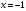 , который требованиям задачи не удовлетворяет. , который требованиям задачи не удовлетворяет. Рассмотрим случай 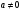 . При таких . При таких  условия (3) запишутся в виде условия (3) запишутся в виде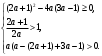 Решая эту систему, находим, что 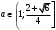 .Очевидно, что этот же результат мы получили бы и решая неравенство .Очевидно, что этот же результат мы получили бы и решая неравенство 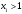 , где , где 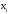 - меньший корень уравнения (1) - меньший корень уравнения (1)Ответ: 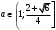 . . 3. Рациональные неравенства с параметрами Пример1. Найти все значения параметра 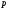 , при которых неравенство , при которых неравенство 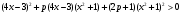 выполняется при всех выполняется при всех 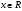 . .Решение. Исходное неравенство является однородным неравенством второй степени относительно функции 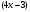 и и 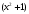 . Если разделить его на . Если разделить его на 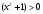 , то получится равносильное неравенство , то получится равносильное неравенство 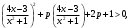 которое после замены 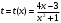 становится квадратным неравенством относительно переменной становится квадратным неравенством относительно переменной  с параметром с параметром 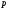 : :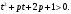 (*) (*)Найдем множество значений функции 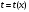 при при 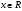 . Имеем: . Имеем: 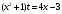 , то есть , то есть 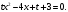 Отсюда Отсюда 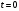 при при 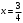 ; другие значения ; другие значения  (отличные от нуля) найдем из условия неотрицательности дискриминанта этого квадратного уравнения: (отличные от нуля) найдем из условия неотрицательности дискриминанта этого квадратного уравнения: 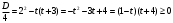 , то есть , то есть 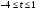 . .Итак, исходное неравенство выполняется для всех 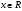 тогда и только тогда, когда неравенство (*) выполняется для всех тогда и только тогда, когда неравенство (*) выполняется для всех 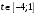 . .Р (1) (2) (3) ассмотрим квадратный трехчлен 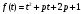 с абсциссой вершины с абсциссой вершины 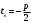 и дискриминантом и дискриминантом 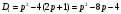 . Тогда имеем следующие необходимые и достаточные условия для нахождения искомых значений параметра . Тогда имеем следующие необходимые и достаточные условия для нахождения искомых значений параметра 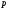 : :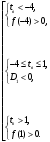 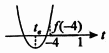 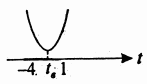 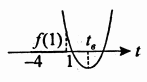 Последовательно преобразуя, получаем: 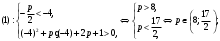 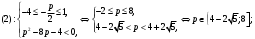 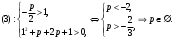 Объединяя решения систем (1)-(3), получаем ответ. Ответ: 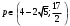 |
