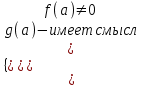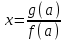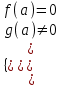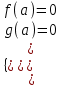сборник. Сборник творческойгруппы. Администрация департамент образования
 Скачать 3.12 Mb. Скачать 3.12 Mb.
|
|
МУНИЦИПАЛЬНОЕ ОБРАЗОВАНИЕ ГОРОД НОЯБРЬСК АДМИНИСТРАЦИЯ ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ЯНАО Задачи с параметрами Материалы городской творческой группы учителей математики по реализации концепции математического образования  Ноябрьск 2015 ВВЕДЕНИЕ. В связи с переходом на профильное обучение возникла необходимость в обеспечении углубленного изучения предмета математики и подготовки учащихся к продолжению образования. Необходимость перехода старшей школы на профильное обучение определена Правительством России в «Концепции математического образования», где ставится задача создания специализированной подготовки (профильного обучения) в старших классах общеобразовательной школы, ориентированной на индивидуализацию обучения и социализацию обучающихся, в том числе с учетом реальных потребностей рынка труда, отработки гибкой системы профилей и кооперации старшей ступени школы с учреждениями начального, среднего и высшего профессионального образования». Принятая в Концепции гибкая система профильного обучения предусматривает возможность разнообразных вариантов комбинаций учебных курсов, осваиваемых старшеклассниками. Эта система включает в себя курсы трех типов: базовые общеобразовательные; профильные общеобразовательные; элективные. Единый государственный экзамен – это словосочетание знакомо сегодня едва ли не каждой семье, в которой есть школьник. Одной из целей проведения ЕГЭ является совмещение итоговой аттестации выпускников и вступительных испытаний для поступления в ВУЗы. Еще одна из целей введения ЕГЭ – попытка улучшения качества образования в России за счет более высокой мотивации на успешное его прохождение. Теперь детей надо готовить к экзаменам по-иному, так, чтобы они сдавали их успешно, а результаты можно было сравнить. Выдерживать такие экзамены – новая задача, как для школьников, так и для педагогов. Можно привести один из главных выводов эксперимента с ЕГЭ: «Впервые за сто лет в России появился объективный и абсолютно прозрачный механизм оценки знаний школьников». На экзаменах прошлых лет в общеобразовательных классах, как правило, задачи с параметрами не решались, а если решались сильными учащимися, то только частично. Каждый ВУЗ предъявляет свои требования к уровню математической подготовки будущего студента, поэтому ВУЗы с большим курсом математики включали в билеты задачи, решить которые, как правило, можно, пройдя специальную целенаправленную подготовку. Вопрос лишь в том, насколько конкурсная задача повышенной сложности обладает диагностической ценностью. Иными словами, можно ли с помощью этой задачи проверить знание основных разделов школьной математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности. Такой диагностической и прогностической ценностью в полной мере обладают задачи с параметрами. Практика вступительных экзаменов в ВУЗы по математике показывает, что задачи с параметрами представляют для абитуриентов наибольшую сложность как в логическом, так и в техническом плане и поэтому умение их решать во многом предопределяет успешную сдачу экзамена в любом высшем учебном заведении. На сегодняшний день задачи с параметрами – неотъемлемая часть ЕГЭ по математике. Сборник посвящен решению задач с параметрами. Умение решать такие задачи считается признаком отличного знания математики. Некоторые при подготовке к экзаменам боятся даже браться за эти задачи, думая, что у них всё равно ничего не получится. Вместе с тем часто для решения задачи с параметром нужно просто использовать свой здравый смысл, и решение окажется простым и понятным!   СОДЕРЖАНИЕ ВВЕДЕНИЕ 1.Салтыкова О.В. Разработка методических рекомендаций решения линейных уравнений и неравенств с параметрами. 2. Афанасьева Е.В. Применение графического метода для решения уравнений с параметрами. 3. Ушакова И.А. Аналитический и графический способы решения линейных уравнений. 4.Соколовская Т.Н. Решение уравнений с параметрами, приводимые к линейным. 5.Кинзябулатова Л.А. Задачи с параметрами при подготовке к ЕГЭ по математике (профильный уровень). 6.Зарецкая И.Ф. Методические рекомендации при изучении различных тем. 7.Ушакова И.А. Упражнения для подготовки к ЕГЭ по математике. ЗАКЛЮЧЕНИЕ Салтыкова О.В. учитель математики МБОУ СОШ №7 Долгий путь начинается с первого шага. (восточная мудрость) Разработка методических рекомендаций решения линейных уравнений и неравенств с параметрами. 1. Алгоритм решения линейных уравнений с параметрами. Исследовать и решить уравнение с параметром – это значит: Найти все системы значений параметров, при которых данное уравнение имеет решение. Найти все решения для каждой найденной системы значений параметров, т.е. для неизвестного и параметра должны быть указаны свои области допустимых значений. На экзаменах встречаются, в основном, два типа задач с параметрами. Для каждого значения параметра найти все решения некоторого уравнения и неравенства. Найти все значения параметра, при каждом из которых для данного уравнения и неравенства выполняются некоторые условия. Определение: Уравнение вида 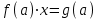 , где , где 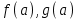 - некоторые аналитические выражение, называется линейным относительно переменной х с параметром а. Если поставлена задача решить такое уравнение, это значит, для каждого допустимого значения параметра а надо найти значение переменной х, удовлетворяющее этому уравнению. - некоторые аналитические выражение, называется линейным относительно переменной х с параметром а. Если поставлена задача решить такое уравнение, это значит, для каждого допустимого значения параметра а надо найти значение переменной х, удовлетворяющее этому уравнению.Алгоритм решения: Найти допустимые значения параметра. Если 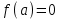 , то существование или отсутствие корней зависит от значения , то существование или отсутствие корней зависит от значения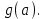 Если Если 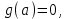 то уравнение принимает вид то уравнение принимает вид 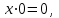 и его корнем служит любое действительное значение переменной х. Если и его корнем служит любое действительное значение переменной х. Если 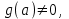 то при любом значении переменной х возникает неверное числовое равенство, то есть уравнение корней не имеет. то при любом значении переменной х возникает неверное числовое равенство, то есть уравнение корней не имеет.Если 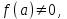 то получим, что то получим, что 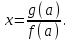 Учащимся можно данный алгоритм предложить оформить в виде таблицы. Алгоритм решения линейных уравнений с параметрами.
2. Решение простейших уравнений с параметрами. Пример 1. Для всех значений параметра а решите уравнение х – а = 0. Ответ: х = а при любом а. Этот пример напоминает, что при решении задач с параметрами нужно находить неизвестную, и указывать, при каких значениях параметра ответ имеет смысл. Пример 2. Для всех значений параметра а решите уравнение 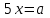 . .Ответ: 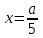 если а – любое число. если а – любое число.Пример 3. Для всех значений параметра а решите уравнение 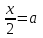 . .Ответ: 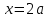 , если а – любое число. , если а – любое число.Пример 4. Для всех значений параметра а решите уравнение ах = 1. Решение: при а = 0 данное уравнение решений не имеет, и в ответе это обстоятельство должно быть отражено. Ответ: при а = 0 решений нет; при а ≠ 0 решение 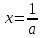 . .Пример 5. Для всех значений параметра а решите уравнение 0х = а. Ответ: при а ≠ 0 корней нет; при а=0 х – любое число. Пример 6. Исследовать и решить уравнение с параметром 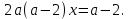 Решение: Найдём контрольные значения параметра, т.е. такие значения при которых коэффициент при х обращается в 0. Такими значениями являются а = 0 и а = 2. а) При а =0 уравнение принимает вид 0х = -2. Это уравнение корней не имеет. б) При а = 2 уравнение принимает вид 0х = 0. Корнем этого уравнения является любое действительное число. в) При а ≠ 0 и а ≠ 2 из исходного уравнения получаем 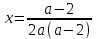 , откуда , откуда 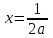 Ответ: 1) при а =0 корней нет. 2) при а = 2 х – любое действительное число. 3) при 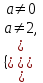 то то 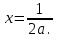 Пример 7. Исследовать и решить уравнение с параметром. 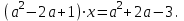 Найдём контрольные значения параметра а: 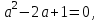 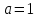 . .а) при а=1 уравнение принимает вид 0х = 0. Корнем этого уравнения является любое действительное число. б) при а ≠ 1 уравнение примет вид 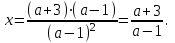 Ответ: 1) при а=1 х – любое действительное число. 2) при а ≠ 1 , то 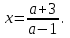 Пример 8. Исследовать и решить уравнение с параметром а2 (х – 5) = 25 (х – а) Выполнив ряд преобразований, приведём уравнение к виду, наиболее удобному для исследования: а2х – 5а2 = 25х – 25а; (а2 – 25)х = 5а2 – 25а. (а-5)(а+5)х = 5а(а-5). а) при 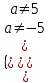 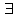 ед. х ед. х 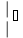 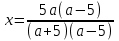 ; ; 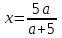 . .б) Если а = 5, то 0х = 0, следовательно, любое х есть решение. в) Если а = - 5, то 0х = 250, следовательно, решений нет. Графическая иллюстрация исследования по параметру а: 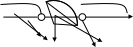 -5 5 -5 5 а 3) 1) 2) Ответ: 1) при 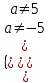 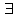 ед. х ед. х 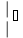 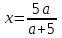 . .2) при а = 5, любое х есть решение. 3. Частные случаи решения линейных уравнений Ученики должны понять, что решение уравнения с параметрами при заданных конкретных условиях – это частные решения уравнений. Например, задание может звучать так: «При каких значениях параметра … уравнение …. Имеет единственное решение или не имеет корней, или имеет корень равный… и т.д.» Пример1. При каких целых значениях параметра а уравнение 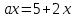 имеет целые корни. имеет целые корни.Решение: Приведём уравнение к виду 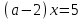 , если , если 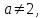 то то 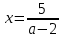 . Чтобы х был целым числом, необходимо, чтобы значение выражения . Чтобы х был целым числом, необходимо, чтобы значение выражения 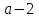 было делителем числа 5, то есть было делителем числа 5, то есть 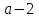 может быть равно 1; -1; 5; -5. Отсюда, а = 3; 1; 7;-3. может быть равно 1; -1; 5; -5. Отсюда, а = 3; 1; 7;-3.Ответ: при а = -3; 1; 3; 7 . Пример 2. При каких значениях параметра n уравнение 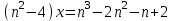 а) имеет единственный корень; б) имеет бесконечное множество корней; в) не имеет корней. Решение: 1. Выражения  имеют смысл при любых значениях n. имеют смысл при любых значениях n.2. Если 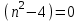 , то , то 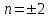 . При . При 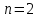 значение выражения значение выражения 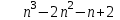 равно 0. Получаем уравнение вида равно 0. Получаем уравнение вида 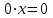 . Оно имеет бесконечное множество корней, то есть х – любое число. При . Оно имеет бесконечное множество корней, то есть х – любое число. При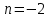 значение выражения значение выражения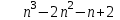 равно – 12, получается уравнение равно – 12, получается уравнение 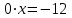 , которое не имеет корней. , которое не имеет корней.3. При 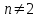 и и 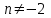 уравнение имеет единственный корень. уравнение имеет единственный корень.Ответ: а) При 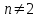 и и 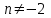 . б) При . б) При 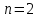 . в) При . в) При 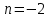 . .Пример 3. При каком значении параметра а уравнение не имеет корней 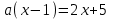 . .Перепишем данное уравнение в виде 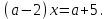 Если а = 2, то уравнение не имеет корней. Ответ: а = 2 Если а = 2, то уравнение не имеет корней. Ответ: а = 2Пример 4. Найдите все значения параметра а, при каждом из которых число 7 является единственным корнем уравнения. Решение: Способ I: Если для некоторого значения параметра число 7 является корнем уравнения, то для этого значения а справедливо равенство 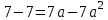 , или равенство , или равенство 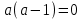 . . Равенство справедливо при а = 0 или при а =1. Мы ещё не получили ответа, так как нашли два значения параметра а, предполагая, что число 7 является корнем уравнения. Но этот корень должен быть единственным, поэтому ещё требуется проверить, является ли число 7 единственным корнем уравнения при а = 0 или при а =1. Если а = 0, то уравнение перепишем в виде х – 7 = 0. При а = 0 число 7 является единственным корнем уравнения. Если же а =1, то уравнение перепишем в виде х - 7 = х – 7. При а=1 любое действительное число является корнем данного уравнения. Следовательно, число 7 не является единственным корнем уравнения. Способ II. Перепишем исходное уравнение в виде 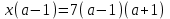 При а =1 корнем уравнения является любое число, то есть число 7 не является единственным корнем уравнения. Поэтому в уравнении а ≠1. Но тогда это уравнение имеет единственный корень 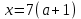 . Условие задачи будет выполнено, если это единственный корень есть число 7: . Условие задачи будет выполнено, если это единственный корень есть число 7: 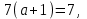 то есть при а = 0. то есть при а = 0.Ответ: а = 0. Пример 5. Найдите все значения параметра а, при каждом из которых уравнения 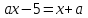 и и 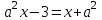 имеют общий корень. имеют общий корень.Решение: Перепишем первое уравнение в виде 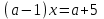 . Это уравнение имеет корень лишь при . Это уравнение имеет корень лишь при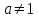 . Этот корень есть число . Этот корень есть число 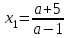 . .Перепишем второе уравнение в виде 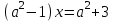 . Данное уравнение имеет корень лишь при . Данное уравнение имеет корень лишь при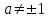 ,. Этот корень есть число ,. Этот корень есть число 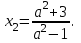 Осталось найти все значения параметра 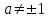 . При каждом из которых первое и второе уравнение имеют общий корень, то есть х1 и х2 есть одно и то же число. . При каждом из которых первое и второе уравнение имеют общий корень, то есть х1 и х2 есть одно и то же число. Для этого решим уравнение 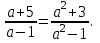 Перенесём все слагаемые в одну часть уравнения и упростим разность алгебраических дробей, равносильное уравнение 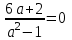 которое имеет единственный корень которое имеет единственный корень 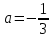 . При этом значении а условие задачи выполнено. . При этом значении а условие задачи выполнено.Ответ: при 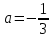 Литература: Натяганов В.Л., Лужина Л.М. Методы решения задач с параметрами: Учеб.пособие. – М.: Изд-во МГУ, 2003. – 368 с. Шахместер А.Х. Уравнения и неравенства с параметрами. – 1-е изд.– СПб.: «ЧеРо-на-Неве», 2004.– 304с. Шахместер А.Х. Задачи с параметрами на экзаменах. – 3-е изд., исправленное.– М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс»,2009. – 248с. Афанасьева Е.В. Зам. директора по УВР МБОУ СОШ №3 Математику затем учить следует, что она ум в порядок приводит. М.В. Ломоносов. Применение графического метода для решения уравнений с параметрами. Если функция задана уравнением y = f (x), разрешенным относительно у, то функция задана в явном виде (явная функция). Будет рассматривать задачи с параметрами, в формулировке которых фигурируют свойства функций. Довольно часто задачу можно переформулировать и свести ее к уравнению, неравенству или системе уравнений (неравенств), для решения которых используют аналитический или функционально-графический способы (графическую интерпретацию). В последнем случае требуется обоснование, основанное на возможности использовании свойств и графиков рассматриваемых функций. Область определения функции. Уравнения, неравенства, системы, да и просто заданные функции, входящие в формулировку задач с параметрами, имеют свою область определения, и анализ условий, определяющих ее, часто является необходимой частью решения. Иногда подобный анализ позволяет существенно сократить количество рассматриваемых случаев, тем самым упростить решение задачи. Говорят, что на числовом множестве X определена числовая функция f (x) , если каждому элементу x из этого множества поставлено в соответствие единственное число. Множество X называется областью определения функции и обозначают D( f ). В задачах с параметром под областью определения уравнения, неравенства, системы, содержащие выражения вида f (x, a) , понимается множество всех упорядоченных пар чисел (x, a) , каждая из которых такова, что после подстановки соответствующих значений x и a во все входящие в задачу выражения они будут определены. Знакомство с параметром. Дадим краткую геометрическую интерпретацию параметру на примере линейной функции. 1). Рассмотрим линейную функцию 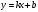 , где k – произвольное число (параметр), принимающее различные значения, b – фиксированное число (рис. 1). Тогда в зависимости от k (углового коэффициента) прямая будет вращаться вокруг точки с координатами , где k – произвольное число (параметр), принимающее различные значения, b – фиксированное число (рис. 1). Тогда в зависимости от k (углового коэффициента) прямая будет вращаться вокруг точки с координатами 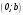 . .2). Рассмотрим линейную функцию 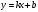 , где b – произвольное число (параметр), принимающее различные значения, k – фиксированное число (рис. 2). Тогда в зависимости от b (свободного коэффициента) прямая будет перемещаться параллельным переносом вдоль оси y. , где b – произвольное число (параметр), принимающее различные значения, k – фиксированное число (рис. 2). Тогда в зависимости от b (свободного коэффициента) прямая будет перемещаться параллельным переносом вдоль оси y.Таким образом, параметр – это неизвестная, при некоторых значениях которой необходимо рассматривать и решать частные уравнения. Эти значения называются особыми. Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они. |


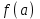 или
или 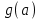 не имеют смысла
не имеют смысла