сборник. Сборник творческойгруппы. Администрация департамент образования
 Скачать 3.12 Mb. Скачать 3.12 Mb.
|
|
Решение уравнений с параметрами, приводимые к линейным. Несложные уравнения с параметром, при решении которых требуется дополнительная проверка, связанная с ограничениями их области определения, составляет следующий шаг в изучении уравнений с параметром. Пример1. Решите уравнение 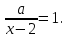 Решение. Очевидно, что х ≠ 2. Умножив обе части уравнения на х–2≠0, получим а = х – 2или х = а + 2. Проверим, нет ли таких значений параметра а, при котором найденное значение х было бы равно числу 2, то есть решим уравнение2 = а + 2 относительно а. Получим, что при а = 0х =2, но число 2 не входит в область определения, следовательно, не может быть его корнем. Ответ: при а = 0 корней нет; при а≠0 х = а +2. Пример2. Решите уравнение 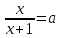 Решение: х ≠ –1. Приведя уравнение к виду (1 — а)х = а, заметим, что при а = 1 уравнение не имеет корней, а при а ≠1 получаем 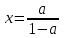 . Решим уравнение . Решим уравнение 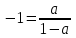 относительно а. Так как уравнение не имеет корней, других вариантов не имеется. относительно а. Так как уравнение не имеет корней, других вариантов не имеется.Ответ: при а ≠1 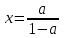 ; при а = 1 корней нет. ; при а = 1 корней нет.Пример 3. Решите уравнение 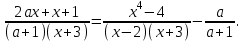 Решение 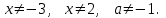 При условии, что При условии, что 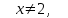 исходное уравнение можно упростить: исходное уравнение можно упростить: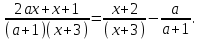 После преобразований получаем уравнение 2ах =1–а, которое при а = 0 не имеет корней, а при а ≠ 0 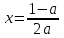 . Проверим, нет ли таких значении параметра а, при которых найденное значение х было бы равно – 3 или 2. для этого решим относительно а уравнения . Проверим, нет ли таких значении параметра а, при которых найденное значение х было бы равно – 3 или 2. для этого решим относительно а уравнения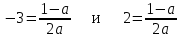 . Корень первого уравнения . Корень первого уравнения– 0,2, корень второго уравнения 0,2, то есть при а ± 0, 2 соответствующие значения х не входят в область определения исходного уравнения. Ответ: при 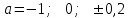 корней нет; при корней нет; при 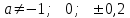 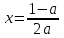 . .Пример 4. Исследовать и решить уравнение с параметром. 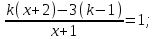 D(у): х≠ -1 . kx+2k – 3k + 3 = x + 1; (k – 1 )x = x + 1 - вид уравнения наиболее удобный для исследования. a) Пусть k≠ 1, тогда существует единственный х 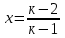 . .б) Выясним, при каких значениях параметра kх = -1, и исключим их. Для этого решим уравнение: 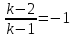 , тогда k = 1,5. , тогда k = 1,5.в) Если k = 1, то 0х = -1, решений нет. Г  рафическая иллюстрация исследования по параметру k рафическая иллюстрация исследования по параметру k1 1,5 k   1) 2) 3) 1) 2) 3)О  твет: 1) При k ≠ 1 твет: 1) При k ≠ 1 k ≠1,5 существует ед. х = 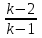 . . 2) При k =1 решений нет. 3) При k = 1,5 решений нет. Пример 5. Исследовать и решить уравнение с параметром. 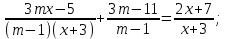 D 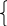 (у): m ≠ 1 (у): m ≠ 1x≠-3. Преобразуем данное уравнение в равносильное с учётом D(у): 3mx – 5 + (3m – 11)(x + 3) = (2x + 7)(m – 1); (4m – 9)x = 31 – 2m - линейное уравнение с параметром, удобное для исследования. а  ) Если m ≠ 2,25 ) Если m ≠ 2,25m ≠ 1 , то существует ед. 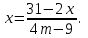 б) Выясним, при каких значениях параметра mx = -3. 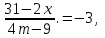 следовательно, m = - 0,4, т.е. при m = - 0,4 х следовательно, m = - 0,4, т.е. при m = - 0,4 х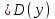 . .в) Если m = 2,25, то 0х = 26,5, следовательно, решений нет. Г  рафическая иллюстрация исследования по параметру рафическая иллюстрация исследования по параметру-0,4 1 2,25 m 1) 3) 4) 2) О  твет: 1) при m ≠ 2,25 твет: 1) при m ≠ 2,25m ≠ - 0,4 существует ед. 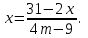 m ≠ 1 2) При m = 2,25 решений нет 3) При m = - 0,4 решений нет 4) При m = 1 уравнение не определено или не имеет смысла. Пример 6. Исследовать и решить уравнение с параметром. 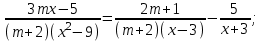 D(y): 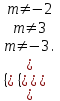 Выполнив необходимые преобразования получим следующее уравнение: Выполнив необходимые преобразования получим следующее уравнение: 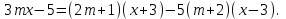 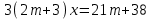 . .а) Если  то то  б)   тогда тогда  т.е. т.е. 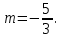 в) 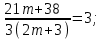 тогда тогда 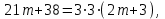 т.е. т.е. 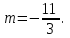 г) 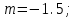 тогда 0= - 6,5, следовательно, решений нет тогда 0= - 6,5, следовательно, решений нетГрафическая иллюстрация исследования c параметром m  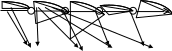 - 2 - 2 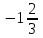 -1,5 -1,5 m 5) 1) 4) 3) 2) Ответ: 1) При 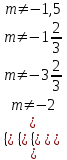 существует единственное решение существует единственное решение 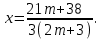 2) При 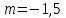 решений нет решений нет3) При 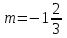 решений нет решений нет4) При  уравнение не определено. уравнение не определено.5) При  решений нет. решений нет.Пример 7. Исследовать и решить уравнение с параметром:  D(y) :  Данное уравнение перепишем в виде 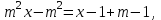 или или 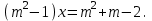 а) Если 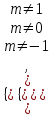 то существует ед. то существует ед. 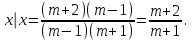 б) Выясним, при каких значениях параметра mx=1, и исключим эти значения, т.е. 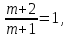 или 2 = 1. Следовательно, не существует такого значения параметра m, при котором x=1, т.е. дополнительных ограничений на значение параметра m нет. или 2 = 1. Следовательно, не существует такого значения параметра m, при котором x=1, т.е. дополнительных ограничений на значение параметра m нет.в) Если m=1, то, 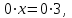 следовательно, любое следовательно, любое 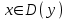 есть решение уравнения, т.е. это случай бесконечного множества решений. есть решение уравнения, т.е. это случай бесконечного множества решений.г) Если m = -1, то 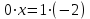 , т.е. решений нет. , т.е. решений нет.д) Если m = 0 - уравнение не определено. Ответ: а) а) Если 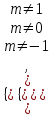 то существует ед. x то существует ед. x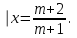 б) Если m=1, то для любого x ≠ 1 есть решение. в) Если m = -1, решений нет г) Если m = 0 - уравнение не определено Литература: Натяганов В.Л., Лужина Л.М. Методы решения задач с параметрами: Учеб.пособие. – М.: Изд-во МГУ, 2003. – 368 с. Шахместер А.Х. Уравнения и неравенства с параметрами. – 1-е изд.– СПб.: «ЧеРо-на-Неве», 2004.– 304с. Шахместер А.Х. Задачи с параметрами на экзаменах. – 3-е изд., исправленное.– М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс»,2009. – 248с. Кинзябулатова Л.А. Учитель математики МБОУ СОШ №7 Руководитель ГМО учителей математики г.Ноябрьск «Математика уступает свои крепости лишь сильным и смелым» А.П. Конфорович Задачи с параметрами при подготовке к ЕГЭ по математике (профильный уровень). Пример 1. Найти все значения а, при каждом из которых оба числа и являются корнями уравнения Решение. Обозначим 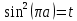 , тогда уравнение примет вид: , тогда уравнение примет вид: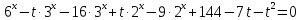 Сгруппируем: 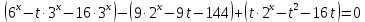 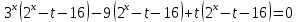 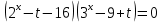 Таким образом: 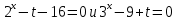 1. Рассмотрим первый корень: 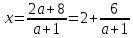 . Подставим его в первое равенство: . Подставим его в первое равенство: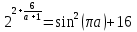 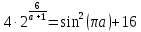 Функция, стоящая слева убывает, приближаясь к 4 сверху при a → ∞ и снизу при a → −∞. Функция, стоящая справа – постоянная величина, принимающая значения из отрезка [16;17]. Таким образом, возможен единственный корень, и корень этот легко найти подбором a = 2. Подставим найденное значение а во второй корень 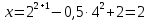 . . Проверим является ли это число корнем первого уравнения: 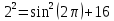 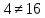 не является корнем. Проверим является ли это число корнем второго уравнения: 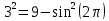 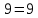 является корнем. 2. Подставим первый корень во второе равенство: 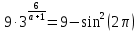 Функция, стоящая слева убывает, приближаясь к 9 сверху при a → ∞ и снизу при a → −∞. Функция, стоящая справа – постоянная величина, принимающая значения из отрезка [8;9] . Таким образом, корень может быть, но при отрицательных a. Но тогда второй корень во втором равенстве дает a = 2, а в первом при положительных a. Противоречие. Ответ: а=2. Пример 2. Найти все значения параметра а, при которых выражение больше выражения при любом значении х, принадлежащем промежутку (2, 5). Решение. Составим неравенство: 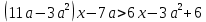 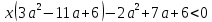 В левой части неравенства стоит линейная функция. Т.к. экстремумов она не имеет, то если знаки этой функции на границах интервала одинаковые, то и на всем интервале функция имеет этот же знак. Таким образом, для выполнения неравенства необходимо, чтобы выполнялась система неравенств 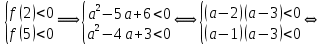 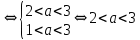 Ответ: (2; 3) Пример 3.Найдите все значения переменной х, при каждом из которых неравенство верно хотя бы при одном значении параметра а из промежутка [3 ; 6]. Решение. Преобразуем данное неравенство. Поскольку обе части неравенства неотрицательны, возведем их в квадрат. 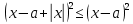 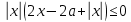 Первый сомножитель неотрицателен, значит 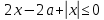 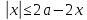 Раскрываем модуль: 1. 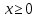 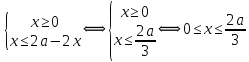 так как 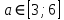 , то , то 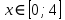 2. 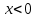 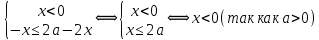 Ответ: 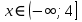 Пример 4. Найти все значения a, при которых неравенство Решение. Преобразуем: 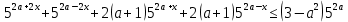 Разделим на 52а: 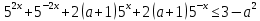 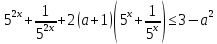 Пусть 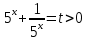 , тогда: , тогда: 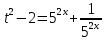 . Неравенство примет вид: . Неравенство примет вид: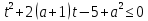 Это парабола, ветви вверх, значит решения не будет если квадратный трехчлен не имеет корней (дискриминант меньше нуля): 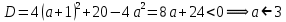 Решений также не будет, если оба корня этого квадратного уравнения не положительные. Из теоремы Виета можно сделать вывод, что это будет выполнено, когда t < 0 , но это невозможно. Еще возможен случай, когда корней вовсе нет. Тогда:  причем при t = 2 корень есть х=0. причем при t = 2 корень есть х=0.Таким образом, решений не будет если все решения попадут в интервал: 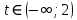 . Для этого необходимо выполнение условий: . Для этого необходимо выполнение условий: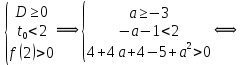 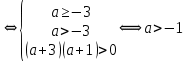 Ответ: 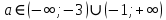 Пример 5. Найдите все значения a > 0, при каждом из которых Решение. Преобразуем: 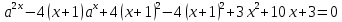 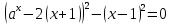 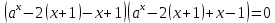 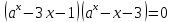 Таким образом: 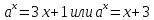 1. Рассмотрим сначала случай a > 1 Прежде всего, уравнение (1) всегда имеет корень х=0, который от значения параметра не зависит. Тогда для выполнения условия задачи надо, чтобы либо уравнение (1) имело еще один корень на указанном промежутке, а уравнение (2) – нет, либо чтоб уравнение (2) имело один корень на этом промежутке, а уравнение (1) – нет. Условия составим на основе сравнения значений функций на границах промежутка. 1. уравнение (1) имеет корень на указанном промежутке, а уравнение (2) – нет: 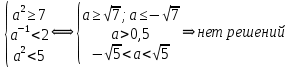 2. уравнение (2) имеет один корень на этом промежутке, а уравнение (1) – нет: 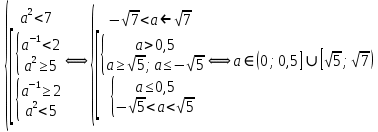 Первый промежуток не удовлетворяет условию a > 1. Значит 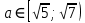 . .Также возможен случай если в уравнении (1) прямая является касательной к графику показательной функции: 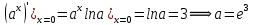 Тогда уравнение (2): 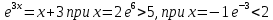 то есть корень попадает в рассматриваемый промежуток. 2. Теперь рассмотрим случай 0 < a < 1 Так как функция 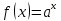 – убывающая, а линейные функции – возрастающая, то здесь каждое уравнение имеет один корень. Причем уравнение (1) всегда имеет корень х = 0 не зависимо от а. Значит для выполнения условия задачи корень уравнения (2) должен попасть в отрезок [-1;2]: – убывающая, а линейные функции – возрастающая, то здесь каждое уравнение имеет один корень. Причем уравнение (1) всегда имеет корень х = 0 не зависимо от а. Значит для выполнения условия задачи корень уравнения (2) должен попасть в отрезок [-1;2]: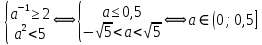 Теперь рассмотрим случай совпадения корней: 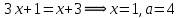 Ответ: 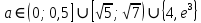 Пример 6. Найдите все значения параметра а, при каждом из которых уравнение Решение Пусть 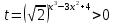 , тогда уравнение примет вид: , тогда уравнение примет вид: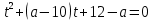 Значит, чтобы исходное уравнение имело 6 корней надо чтобы данный квадратный трехчлен имел два различных корня, то есть: 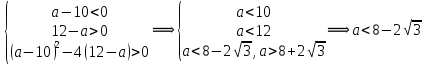 При каждом из этих положительных t кубическое уравнение  должно иметь именно три различных корня. Рассмотрим функцию должно иметь именно три различных корня. Рассмотрим функцию   Найдем максимальное и минимальное значения:  функция имеет максимум в точке (0; 4) и минимум в точке (2; 0). Кубическое уравнение будет иметь ровно три корня, если значение функции f попадет в промежуток 0 < f ( x ) < 4 , тогда 1 < t < 4 . Получили ограничение на корни исходного квадратного (относительно t) уравнения. Поскольку ветви параболы 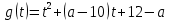 направлены вверх, то для того, чтобы корни находились внутри данного интервала достаточно условия, чтоб эти корни вообще были (это учтено выше), чтоб вершина параболы была внутри интервала, и значения функции на границах интервала были положительны. Получаем: направлены вверх, то для того, чтобы корни находились внутри данного интервала достаточно условия, чтоб эти корни вообще были (это учтено выше), чтоб вершина параболы была внутри интервала, и значения функции на границах интервала были положительны. Получаем: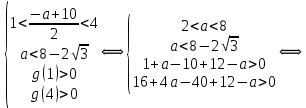 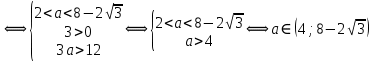 Ответ: 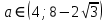 Пример 7. Найдите все значения параметра а, при которых уравнение Решение. Как сразу видно, это уравнение всегда имеет корень x = 0 независимо от значения параметра. Поэтому уравнение 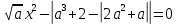 не должно иметь корней. не должно иметь корней.Преобразуем: 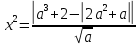 Так как справа неотрицательное число, значит это уравнение всегда имеет решение. Тогда чтобы выполнялось условие (ровно один корень) надо чтоб это уравнение имело один корень х=0: 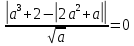 Заметим, что при а = 0 исходное уравнение имеет единственный корень х = 0. 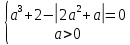 Так как 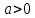 , то , то 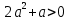 , значит модуль можно опустить: , значит модуль можно опустить: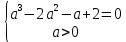 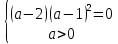 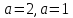 Ответ: а=0;1;2. Пример 8. Найдите все значения а, при каждом из которых уравнение Решение. Преобразуем: 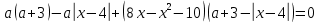 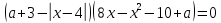 Тогда: 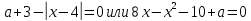 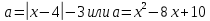 Рассмотрим функции: 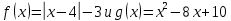 . параллельным переносом прямой h(x)=a, определим где эта прямая пересекает f(x) и g(x) в двух точках: . параллельным переносом прямой h(x)=a, определим где эта прямая пересекает f(x) и g(x) в двух точках: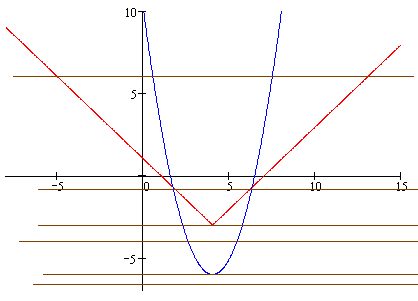 Как видно по графику два корня уравнение будет иметь от вершины параболы до вершины «галочки», а также в точке где «галочка» и парабола пересекаются. Вершина параболы: 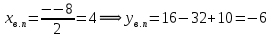 Вершина «галочки»: 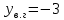 . .Графики пересекаются: 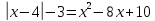 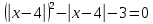 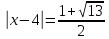 Тогда: 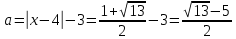 Ответ: 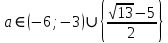 Пример 9. При каких положительных значениях параметра а модуль разности корней уравнения не больше расстояния между точками экстремума функции Решение Найдем точки экстремума: 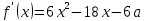 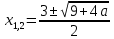 Расстояние между точками экстремума:  . .Корни уравнения:  Модуль их разности:  Составим неравенство:  Так как обе части неравенства положительны, возведем в квадрат:    Найдем нули выражения, стоящего во вторых скобках:   Тогда:  Отсюда:  По условию а – положительное, поэтому  Ответ:  Пример 10. Найдите все значения а, при которых каждое из уравнений Решение Посмотрим сначала когда первое уравнение имеет корни.  Рассмотрим функции:  и и  . Точка пересечения этих графиков должна попасть в отрезок [-1;1] поскольку t = cosx . Точка пересечения этих графиков должна попасть в отрезок [-1;1] поскольку t = cosx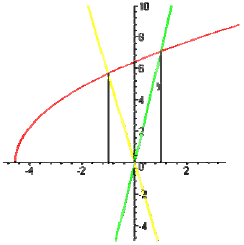 Вращая прямую 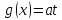 около начала координат получим что графики будут пересекаться в отрезок [-1;1] начиная с около начала координат получим что графики будут пересекаться в отрезок [-1;1] начиная с 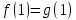 до до 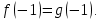 Решаем: 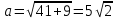 и 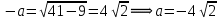 Таким образом: 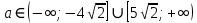 Рассмотрим второе уравнение: 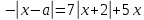 Функция, стоящая в правой части достигает своего наименьшего значения -10 в точке x = −2. График функции в левой части представляет собой «перевернутый» график модуля, смещенный по оси абсцисс на величину а. Для того чтобы уравнение имело корни, должно быть выполнено условие     Тогда пересечение найденных область дает искомые значения а. Ответ: 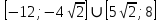 Пример 11. Найдите все неотрицательные значения параметра а, при которых уравнение Решение. Преобразуем: 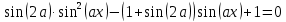 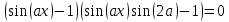 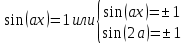 Решаем первое уравнение:    Условие попадания в отрезок:  Из первого и последнего неравенств системы:  Т.к. k ∈ Z , то k = −1,−2,−3,−4,−5  Решение имеет только система при k = -3 тогда  Теперь второй случай. при  получаем попадание в промежуток получаем попадание в промежуток  . Т.е. этот случай учтен. . Т.е. этот случай учтен.Если уравнение sin(ax) = 1 имеет два корня на отрезке [− π ;π ], то и уравнение sin(ax) = −1 тоже имеет там два корня при тех же значениях параметра. В этом легко убедиться: Для   Из первого и последнего неравенств системы:  Т.к. k ∈ Z , то k = −1,−2,−3 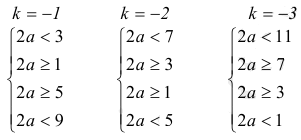 Решение имеет только система при k = −2, тогда 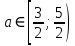 Для 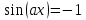 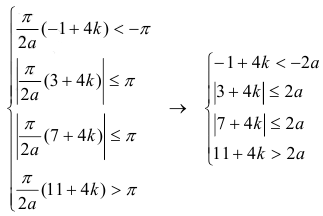 Из первого и последнего неравенств системы:  Т.к. k ∈ Z , то k = 0,−1,−2  Решение имеет только система при k = −1, тогда  При этом  попадает в этот промежуток при попадает в этот промежуток при  . .А вот  в этот промежуток не попадает. в этот промежуток не попадает. Значит, при  будет ситуация, когда будет два корня по первому рассмотренному случаю и два корня по второму. будет ситуация, когда будет два корня по первому рассмотренному случаю и два корня по второму.И наконец, случай, когда квадратное уравнение будет линейным. при этом  но ни при каком n не будет попадания в промежуток но ни при каком n не будет попадания в промежуток 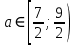 . Т.е. четырех корней не будет . Т.е. четырех корней не будетОтвет: 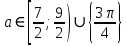 Пример 12. При каких значениях а уравнение Решение. Преобразуем: 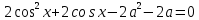 На участке [0; 2π) любое значение косинуса будет давать 2 значения угла кроме точек x = 0 и x= π, тогда значение угла будет единственным Пусть x = 0: 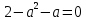 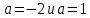 при этом 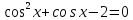 имеет единственное решение х=0. Пусть x = π: 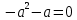 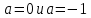 при этом 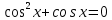 имеет два решения х=0 и x= π. Ответ: 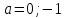 Пример 13. Найти все а, при которых уравнение имеет нечетное число решений на интервале . Решение. Введем обозначения: 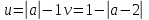 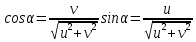 Тогда: 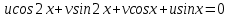 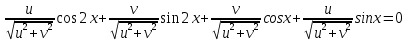 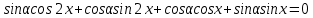 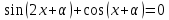 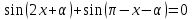 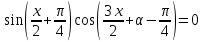 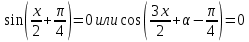 |
