сборник. Сборник творческойгруппы. Администрация департамент образования
 Скачать 3.12 Mb. Скачать 3.12 Mb.
|
|
4.Иррациональные уравнения с параметрами Существует несколько способов решения иррациональных уравнений с параметрами. Познакомимся с ними, разобрав следующий пример. Пример. В зависимости от значений параметра  решить уравнение решить уравнение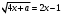 (1) (1)Решение. Решим уравнение (1) пятью способами, которые необходимо знать, ибо наряду с другими подходами они могут быть использованы и при решении иных типов уравнений. Способ 1. Уравнение (1) равносильно системе 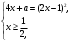 или системе 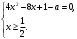 (2) (2)Решая уравнение из системы (2), находим 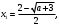 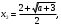 (3) (3)откуда следует, что при 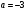 уравнение (1) имеет одно решение уравнение (1) имеет одно решение 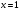 . Если . Если 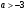 , то , то 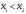 , и тогда уравнение (1) будет иметь два решения при тех значениях параметра , и тогда уравнение (1) будет иметь два решения при тех значениях параметра  , при которых совместна система , при которых совместна система 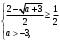 , ,т.е. при 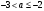 Уравнение (1) будет иметь только один корень 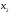 , если , если 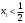 , а , а 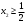 . В этом случае решая систему . В этом случае решая систему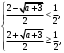 приходим к выводу, что 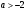 . .Замечая теперь, что при 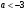 дискриминант уравнения системы (2) отрицателен, получаем дискриминант уравнения системы (2) отрицателен, получаемОтвет: если 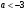 , то решений нет; , то решений нет;если 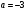 , то , то 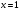 ; ;если 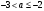 , то , то 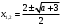 ; ;если 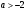 , то , то 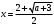 . .Способ 2. Возведя обе части уравнения (1) в квадрат, получим уравнение из системы (2), корни которого задаются формулами (3). Но здесь надо иметь в виду, что при возведении обеих частей уравнения (1) в квадрат могли появиться посторонние корни. Поэтому при данном способе решения необходимо произвести проверку. Так, подставляя корень 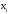 в исходное уравнение, придем к соотношению в исходное уравнение, придем к соотношению 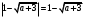 , ,откуда 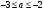 . .Если же подставить корень 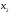 в уравнение (1), то придем уже к отношению в уравнение (1), то придем уже к отношению 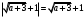 , и, таким образом, , и, таким образом, 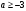 . .Учитывая теперь, что при 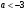 корней нет, а при корней нет, а при 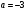 имеем имеем 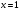 , получаем тот же ответ, что и при первом способе решения. , получаем тот же ответ, что и при первом способе решения.Способ 3. Если воспользоваться геометрическим смыслом квадратного трехчлена, то, обращаясь к равносильной уравнению (1) в системе (2), приходим к выводу, что уравнение (1)будет иметь корни 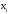 и и 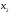 в том случае, когда корни квадратного трехчлена в том случае, когда корни квадратного трехчлена 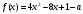 не меньше не меньше 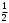 . Аналитически соответствующие условия записываются в виде системы . Аналитически соответствующие условия записываются в виде системы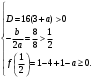 Решая эту систему, находим, что 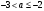 . .При 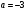 уравнение (1) имеет решение уравнение (1) имеет решение 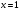 . .Если же 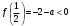 , т.е. , т.е. 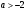 , то уравнение (1) будет иметь один корень , то уравнение (1) будет иметь один корень 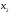 . При . При 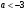 решений нет. решений нет.Способ 4. Рассмотрим графики функций 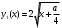 и и 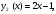 заданных соответственно левой и правой частями уравнения (6.1). 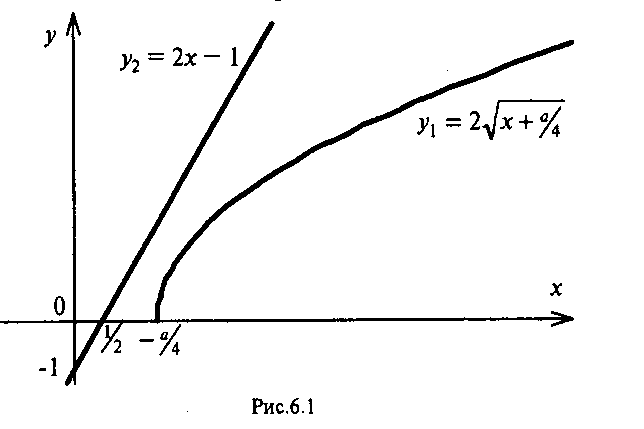 Абсциссы точек пересечения этих графиков и будут решениями уравнения (1). При 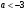 графики не пересекаются (см. рис. 6.1) и значит уравнение (1) решений не имеет. графики не пересекаются (см. рис. 6.1) и значит уравнение (1) решений не имеет.При 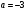 графики касаются и уравнение (1) имеет один корень графики касаются и уравнение (1) имеет один корень 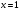 . .При 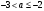 уравнение (1) будет иметь корни уравнение (1) будет иметь корни 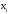 и и 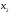 , определяемые формулами (3) (см. рис. 6.2). , определяемые формулами (3) (см. рис. 6.2).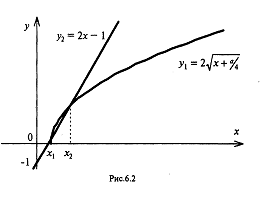 При 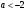 графики функций графики функций 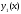 и и 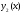 пересекаются в одной точке, и значит уравнение (1) имеет одно решение пересекаются в одной точке, и значит уравнение (1) имеет одно решение 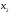 (см. рис. 6.3) (см. рис. 6.3)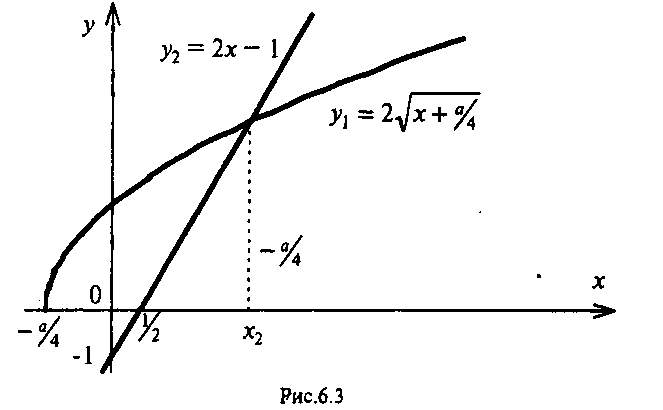 Способ 5. Перепишем равносильную уравнению (1) систему (2) в виде 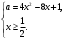 Построив тогда в плоскости 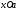 график функции график функции 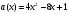 при условии при условии 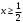 (см. рис. 6.4), мы приходим к выводам, полученным ранее четырьмя рассмотренными способами. (см. рис. 6.4), мы приходим к выводам, полученным ранее четырьмя рассмотренными способами. 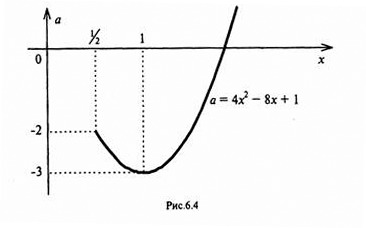 Ответ: если 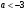 , то решений нет; , то решений нет;если 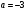 , то , то 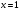 ; ;если 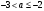 , то , то 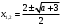 ; ;если 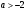 , то , то 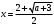 . . 5.Показательные и логарифмические неравенства с параметрами Пример1. Найти все значения параметра  , при которых неравенство , при которых неравенство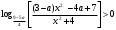 выполняется для всех действительных значений  . .Решение. Исходное неравенство 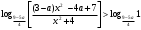 равносильно следующей совокупности двух систем: 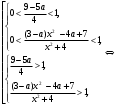 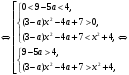 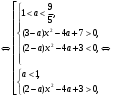 (1) (2) (1) (2) В системе (1) параметр 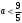 , поэтому коэффициент , поэтому коэффициент 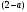 , стоящий при , стоящий при 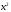 в левой части последнего неравенства, положителен, следовательно, последнее неравенство системы (1) равносильно неравенству в левой части последнего неравенства, положителен, следовательно, последнее неравенство системы (1) равносильно неравенству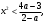 которое не может выполняться при всех действительных значениях которое не может выполняться при всех действительных значениях  при любом фиксированном значении параметра при любом фиксированном значении параметра  . Таким образом, система (1) не дает искомых значений параметра. . Таким образом, система (1) не дает искомых значений параметра.В системе 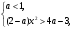 (2) (2)из первого неравенства ( 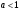 ) так же, как и раньше, вытекает, что ) так же, как и раньше, вытекает, что 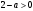 , следовательно, второе неравенство равносильно неравенству , следовательно, второе неравенство равносильно неравенству 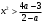 , ,которое, очевидно, выполняется для всех действительных  тогда и только тогда, когда тогда и только тогда, когда 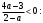 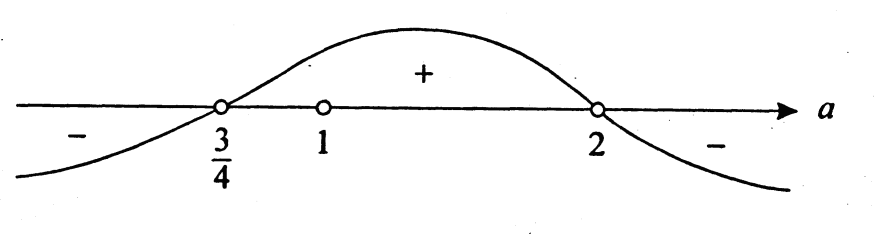 С учетом того, что 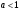 , получаем , получаем 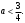 Ответ: 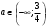 6.Производная и ее применения. Пример1. Найти все значения параметра  , при которых функция , при которых функция 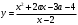 имеет хотя бы один экстремум строго между числами имеет хотя бы один экстремум строго между числами  и и 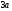 . .Решение. Для вычисления экстремумов функции 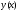 найдем её производную: найдем её производную: 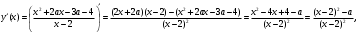 откуда следует, что в точках экстремума, то есть при откуда следует, что в точках экстремума, то есть при 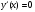 , значение параметра , значение параметра 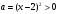 , так как , так как 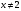 . Поэтому интервал . Поэтому интервал 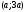 , на котором, согласно условию задачи, надо искать экстремум, целиком расположен справа от точки 0. , на котором, согласно условию задачи, надо искать экстремум, целиком расположен справа от точки 0.Дальнейшее решение задачи изложим двумя способами. Способ 1. Рассмотрим квадратный трехчлен 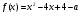 с абсциссой вершины с абсциссой вершины 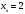 и дискриминантом и дискриминантом 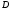 , положительность которого следует из того, что , положительность которого следует из того, что 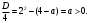 Если абсцисса 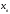 вершины параболы, являющейся графиком функции вершины параболы, являющейся графиком функции 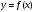 , расположена левее интервала , расположена левее интервала 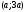 , то есть величина , то есть величина 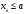 , то значения , то значения 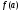 и и 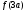 должны быть разных знаков, причем должны быть разных знаков, причем 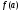 - отрицательно: - отрицательно: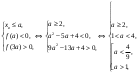 откуда следует, что 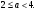 Если 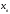 лежит строго между лежит строго между  и и 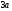 , то либо , то либо 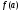 , либо , либо 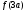 должно быть положительно: должно быть положительно: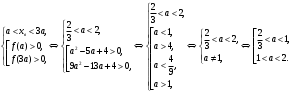 Если 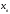 лежит правее интервала лежит правее интервала 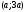 , то есть , то есть 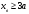 , то значения , то значения 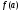 и и 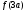 должны быть разных знаков, причем должны быть разных знаков, причем 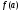 - положительно: - положительно: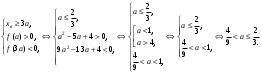 Объединяя найденные значения параметра  в рассмотренных трех случаях в рассмотренных трех случаях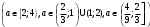 , получает ответ: , получает ответ: 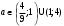 . .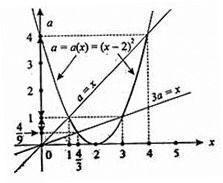 Способ 2. Способ 2.Как мы уже получили ранее, в точках экстремума, то есть при 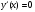 имеем имеем 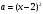 . В плоскости . В плоскости 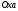 нарисуем график функции нарисуем график функции 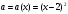 . Точки экстремума будем искать на интервале . Точки экстремума будем искать на интервале 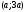 , то есть при , то есть при 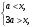 что соответствует внутренним точкам острого угла, ограниченного прямыми что соответствует внутренним точкам острого угла, ограниченного прямыми 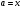 и и 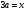 , и находящегося в первой четверти. Найдем точки пересечения прямых , и находящегося в первой четверти. Найдем точки пересечения прямых 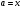 и и 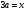 с параболой с параболой 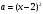 . Решая квадратные уравнения, получаем: . Решая квадратные уравнения, получаем: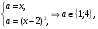 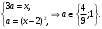 Так как производная 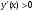 при при 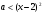 и и 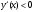 при при 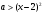 , то исходная функция , то исходная функция 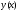 является возрастающей в области является возрастающей в области 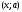 , расположенной ниже параболы , расположенной ниже параболы 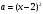 , и убывающей в области, расположенной выше этой параболы; в точках параболы функция , и убывающей в области, расположенной выше этой параболы; в точках параболы функция 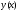 имеет экстремум (в силу того, что выполнено достаточное условие экстремума – смена знака производной). имеет экстремум (в силу того, что выполнено достаточное условие экстремума – смена знака производной).Левая ветвь параболы 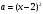 пересекается с прямыми пересекается с прямыми 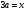 и и 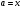 в точках в точках 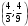 и и 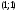 соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции 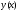 , соответствующим искомым значениям параметра , соответствующим искомым значениям параметра  : : 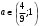 (проекция на ось (проекция на ось 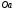 указанного участка левой ветви параболы указанного участка левой ветви параболы 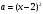 ). ).Правая ветвь параболы 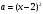 пересекается с прямыми пересекается с прямыми 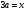 и и 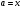 в точках в точках 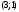 и и 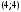 соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции соответственно. Все точки параболы, расположенные строго между этими точками пересечения, отвечают точкам экстремума функции 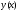 , соответствующим искомым значениям параметра , соответствующим искомым значениям параметра  : : 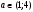 (проекция на ось (проекция на ось 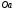 указанного участка правой ветви параболы указанного участка правой ветви параболы 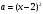 ). ).Объединяя найденные выше интервалы 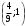 и и 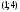 значений параметра значений параметра  , получаем ответ. , получаем ответ.Ответ: 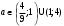 . .Литература: 1. Высоцкий В. С. Задачи с параметрами при подготовке к ЕГЭ. – М.: Научный мир, 2011. – 316 с. 2. ЕГЭ 2013. Математика: Сборник тренировочных работ / Высоцкий И.Р., Захаров П.И., Панфёров В.С., Семёнов А.В., Сергеев И.Н., Смирнов В.А., Шестаков С.А., Ященко И.В. – М.: МЦНМО, 2010. Ушакова И.А. Учитель математики МБОУ СОШ №3 Упражнения для подготовки к ЕГЭ по математике.  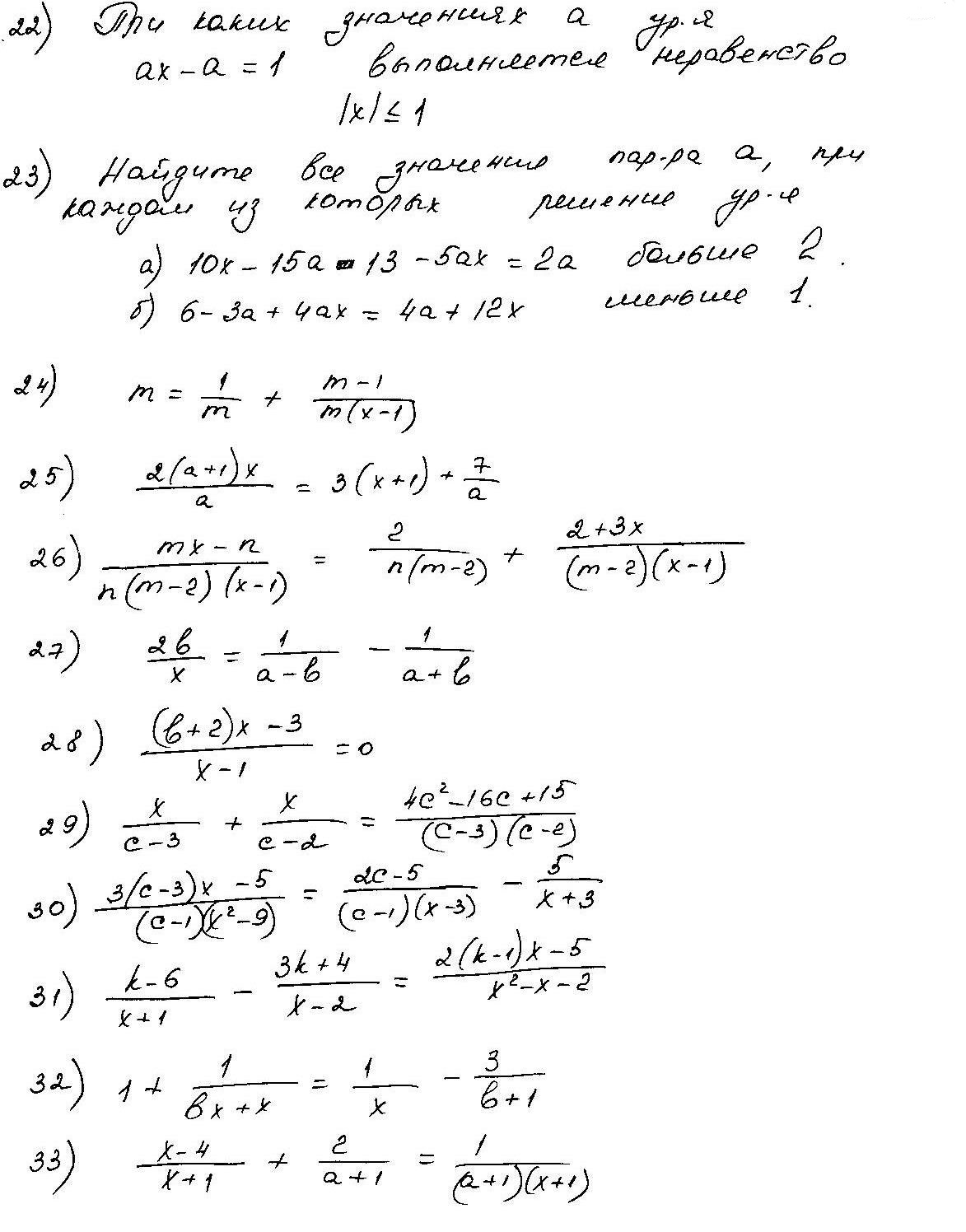     Литература: 1. Высоцкий В. С. Задачи с параметрами при подготовке к ЕГЭ. – М.: Научный мир, 2011. – 316 с. 2. ЕГЭ 2013. Математика: Сборник тренировочных работ / Высоцкий И.Р., Захаров П.И., Панфёров В.С., Семёнов А.В., Сергеев И.Н., Смирнов В.А., Шестаков С.А., Ященко И.В. – М.: МЦНМО, 2010. 3. Корянов А.Г., Прокофьев А.А. Использование метода наглядной графической интерпретации при решении уравнений и неравенств с параметрами // Математика в школе. М.: ООО «Школьная пресса», 2011, №1 (начало) – С. 18-26, №2 (окончание) – С. 25-32. 4. Корянов А.Г., Прокофьев А.А. Различные подходы к решению задач С5 ЕГЭ // Математика. М.: Издательский Дом «Первое сентября», 2011, № 5 − С.11–21. Научное издательство «Большая Российская энциклопедия», 1996, – 527 с. 5. Неравенства с двумя переменными: графическое и аналитическое решения / А. Корянов. – М.: Чистые пруды. 2008. (Библиотечка «Первого сентября», серия «Математика». Вып. 22). 6. Панферов В.С., Сергеев И.Н. Отличник ЕГЭ. Математика. Решение сложных задач; ФИПИ – М.: Интеллект-Центр, 2010. 7. Прокофьев А.А., Шабунин М.И. Системы уравнений и неравенств с двумя переменными // Журнал «Потенциал», 2011, №3 – С. 29-36. 8. Прокофьев А.А. Задачи с параметрами. Учебное пособие. – М.: МИЭТ, 2004. 9. Сергеев И. Н. ЕГЭ: 1000 задач с ответами и решениями по математике. Все задания группы С / И. Н. Сергеев, В. С. Панферов. – М.: Издательство «Экзамен», 2012. – 301 с. 10. Сергеев И. Н. ЕГЭ. Практикум по математике: подготовка к выполнению части С / И. Н. Сергеев, В. С. Панферов. – М.: Издательство «Экзамен», 2012. 11. Ященко И.В., Шестаков С.А., Захаров П.И. Подготовка к ЕГЭ по математике в 2012 году. Методические указания. – М.: МЦНМО, 2012. – 208 с. ЗАКЛЮЧЕНИЕ В сборнике предоставлены материалы учителей математики города Ноябрьск, которые позволили выявить основные методы решения задач с параметрами и адаптировать их к школьному курсу. Что помогло составить систему дидактических материалов, которые можно использовать для учащихся 7 – 11 классов в процессе усвоения той или иной темы или для параллельного повторения при подготовке к ГИА или ЕГЭ. |
